Моделирование динамики сообщества хищник-жертва с возрастной структурой жертвы и изъятием

Целью работы является изучение влияния антропогенного изъятия на динамику сообщества «хищник-жертва». Исследуемая модель представляет собой модификацию модели Николсона-Бейли, в которой учитываются возрастная структура жертвы и плотностное лимитирование выживаемости молоди жертвы [1]. Предполагается, что хищничеству подвергаются молодые особи жертвы, при этом рассмотрение возрастной структуры хищника не требуется. Это может быть связано с тем, что возрастная структура хищника отсутствует или он представлен популяцией с непересекающимися поколениями, или его жизненный цикл оказывается намного короче, чем у жертв, или незрелые стадии хищника тоже участвуют в хищничестве, поэтому выделение возрастной структуры оказывается не принципиальным. С учетом антропогенного изъятия система имеет вид:

' x n + 1 = ry n exp( - Z n ) ⁾⁽¹ - u 1 )

• < У п + 1 = ^(e xp ⁽ - Pnn - У) x n ⁺ У n ⁾⁽¹ - u 2 ) , ⁽1) . z n + 1 = ^СГ У п ⁽¹ - ^e xP ⁽ - Z n ) ⁾⁾⁽¹ - u 3 )

где n – номер поколения; x и y – относительные численности младшего и старшего возрастных классов популяции жертвы соответственно; z – относительная численность популяции хищника; r – репродуктивный потенциал популяции жертвы; v – коэффициент выживаемости взрослых особей жертвы; ρ – относительный вклад младшей возрастной группы в лимитирование выживаемости молоди популяции жертвы; γ – относительная скорость потребления жертвы хищником; c – скорость трансформации биомассы жертвы в хищников; u1 и u2 – доли изъятия молоди и взрослых особей популяции жертвы соответственно; u3 – доля изъятия хищников.

Исследованы частные случаи модели (1), когда осуществляется частичное изъятие особей из младшего ( u ₁; u ₂ = u ₃ = 0) или старшего ( u ₂; u ₁ = u ₃ = 0) возрастного класса жертвы, либо из двух возрастных классов жертвы с равной интенсивностью ( u ₁ = u ₂; u ₃ = 0), либо из популяции хищника ( u ₃; u ₁ = u ₂ = 0).

Для всех случаев системы (1) найдены координаты полутривиальной и нетривиальной неподвижных точек и построены области их устойчивости. Показано, что устойчивое сосуществование взаимодействующих видов становится возможным в случае, если имеют место транскритическая ( TC ) или седло-узловая ( SN ) бифуркации. Благодаря седло-узловой бифуркации в системе взаимодействующих популяций наблюдается бистабильность динамики: в зависимости от начальных условий хищник либо сосуществует с жертвой, либо погибает.

Выявлено, что потеря устойчивости неподвижных точек для частных случаев системы (1) может осуществляться по сценарию Неймарка-Сакера ( NS ), что приводит к возникновению квазипериодических режимов, или по сценарию удвоения периода ( PD ), при 210

котором возникают регулярные колебания численностей видов.

Показано, что изъятие доли молодых особей из популяции жертвы ( u ₁) приводит к сужению области значений параметров, при которых жертва существует в отсутствии хищника, но при этом расширяется область значений параметров, при которых взаимодействующие виды устойчиво сосуществуют (рис.). Увеличение доли изъятия u ₁ приводит к стабилизации динамики жертвы в отсутствии хищника и сужению области бистабильности динамики.

При изъятии части взрослых особей из популяции жертвы ( u ₂) устойчивое сосуществование сообщества «хищник-жертва» становится возможным при более высоких значениях репродуктивного потенциала жертвы r (рис.). При этом рост доли изъятия u ₂ приводит к расширению области бистабильности.

В случае изъятия части особей из двух возрастных классов с одинаковой интенсивностью ( u ₁ = u ₂) происходят стабилизация динамики жертвы без хищника и уменьшение области бистабильности. Одновременно с этим устойчивое сосуществование взаимодействующих видов происходит при более высоких значениях коэффициента рождаемости жертвы r (рис.).

Следовательно, изъятие только молодых особей жертвы или вместе со взрослыми позволяет добиться устойчивой динамики популяции жертвы как с хищником, так и без него в большей параметрической области, чем добыча лишь взрослых особей. Также уменьшается диапазон значений параметров, при которых отмечается бистабиль-

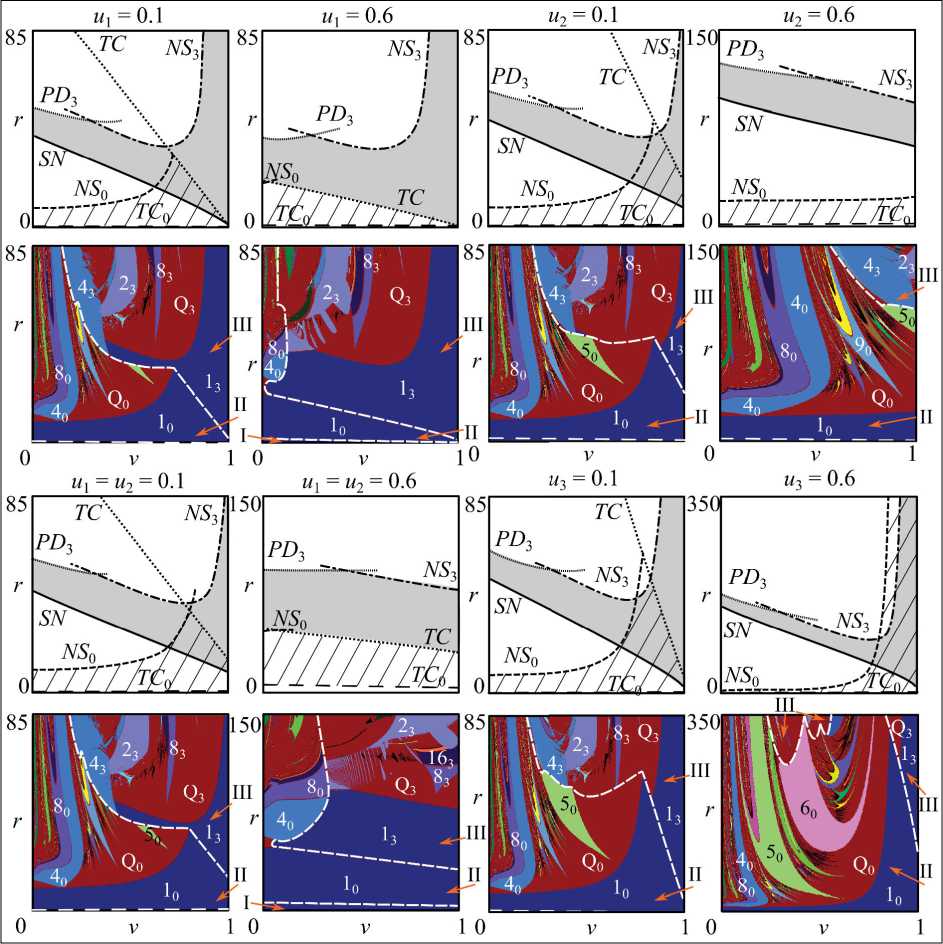
Рис. Области устойчивости неподвижных точек и карты динамических режимов (при x0 = 3.3546, y0 = 0.0965, z0 = 0.01) системы (1) при γ = 0.33, ρ = 1.5, c = 0.9 и разных значениях доли изъятия ui (i = 1, 2, 3). Штриховкой и заливкой выделены области устойчивости полутривиального и нетривиального равновесия соответственно. Числа на картах указывают на длину цикла, Q – квазипериодическая динамика. Нижние индексы 0 и 3 соответствуют полутривиальному и нетривиальному равновесию и режимам, возникающим в результате их бифуркаций. Области I – гибель обоих видов; II – жертва существует без хищника; III – жертва и хищник сосуществуют

Fig. Areas of stability of fixed points and maps of dynamic modes (at x0 = 3.3546, y0 = 0.0965, z0 = 0.01) of the system (1) at y = 0.33, p = 1.5, c = 0.9 and different values of the withdrawal fraction ui (i = 1, 2, 3). Shading and fi lling are the areas of stability of semi-trivial and non-trivial equilibrium, respectively. The numbers on the maps indicate the length of the cycle; Q is the qua-si-periodic dynamics. The subscripts 0 and 3 correspond to semi-trivial and non-trivial equilibria and the modes resulting from their bifurcations. Areas I – death of both species; II-prey exists without a predator; III-prey and predator coexist ность динамики, т.е. поведение сообщества становится более предсказуемым.

Усиление интенсивности изъятия части хищников u ₃ приводит к тому, что совместное обитание жертвы и хищника обеспечивается высокими значениями коэффициента рождаемости r (рис.). Аналогично изъятию молодых особей жертвы, при изъятии хищников увеличение значений выживаемости взрослых особей жертв v приводит к стабилизации динамики видов.