Моделирование доплеровского сдвига частоты в многолучевых радиоканалах

В настоящее время наиболее часто используемым способом измерения доплеровского смещения частоты является спектральный анализ [Baddeley et al., 2005; Bianchi, Altadill, 2005; Petrova et al., 2009]. В рамках данного подхода для квазимонохромати-ческого сигнала в случае стационарной среды и постоянной скорости излучателя или приемника мы получаем ярко выраженный пик, положение которого и определяет сдвиг частоты (классический эффект Доплера).

Для нестационарной среды и меняющейся со временем скорости приемника или излучателя мы получим так называемый доплеровский спектр, потеряв при этом детальное поведение сдвига частоты в зависимости от времени, которое мы далее будем называть тонкой структурой эффекта Доплера. Стоит от- метить, что трактовка доплеровского спектра неоднозначна и зависит от условий поставленной задачи.

Примером такой нестационарной среды является ионосфера. При измерении спектральными методами доплеровского смещения частоты квазимонохрома-тического сигнала, прошедшего нестационарный ионосферный радиоканал, мы ограничены двумя факторами: дисперсия не позволяет сформировать слишком короткий сигнал, а нестационарность не дает анализировать слишком длинные сигналы. Характерные значения доплеровских (параметрических) сдвигов частоты квазимонохроматического радиосигнала в КВ-диапазоне, прошедшего ионосферный радиоканал, составляют герцы или доли герца. Для измерения подобных величин необходимы сигналы длительностью до десятков секунд, но неста-ционарность радиоканала накладывает ограничения на использование таких сигналов.

Иным подходом, позволяющим измерить тонкую структуру сдвига частоты, является анализ фазы сигнала. В случае однолучевого сигнала это не представляется слишком сложной задачей. Однако при прохождении непрерывного сигнала через многолучевой радиоканал поведение фазы становится довольно сложным, поскольку отражает поведение суммы фаз лучей, а не поведение фазы отдельно взятого луча. Задача разделения лучей такого сигнала является некорректной и в общем случае нерешаемой.

Вместо непрерывного сигнала можно использовать импульсный сигнал, который в точке приема можно разделить на отдельные лучи по задержкам. Дисперсия и нестационарность канала незначительно влияют на импульсы, ширина полосы которых существенно меньше полосы когерентности канала (порядка сотен килогерц [Иванов и др., 2006]), а длительность сравнима со временем распространения и существенно меньше характерного времени изменения параметров канала. Радиоканал можно считать стационарным во время распространения одного такого импульса, но одиночные импульсы не позволяют измерить скорости изменения ионосферных параметров. В этом случае можно регистрировать либо спектр последовательности импульсов [Бату-хин и др., 2000], который является линейчатым, либо амплитуду и фазу каждого отдельного импульса с последующим анализом их изменений с течением времени.

В общем случае изменение параметров ионосферного радиоканала с течением времени приводит к изменениям характеристик отдельных импульсов. Однако несложно установить, что при спектральных измерениях когерентной последовательности импульсов только вариации фазы передаточной функции канала (которая и определяет среднюю фазу амплитудно-модулированного импульса) приводят к изменению положения центральной спектральной линии в линейчатом спектре. При этом вариации амплитуды или задержки к сдвигам центральной линии не приводят. Вариации амплитуды приводят к деформации спектральных линий, а вариации задержки приводят к малому изменению расстояния между спектральными линиями, не меняя положение и форму центральной линии.

Таким образом, в случае малых вариаций ионосферных параметров фаза и амплитуда сигнала будут непрерывно меняться от импульса к импульсу, при этом изменение амплитуды можно не учитывать. Скорость же изменения фазы можно трактовать как доплеровское смещение частоты [Barnes, 1992; Cohen, 1995].

Исходя из этого, имея модель передаточной функции многолучевого радиоканала, параметры которого медленно и непрерывно меняются с течением времени, мы можем регистрировать фазу отдельных импульсов, соответствующих отдельным лучам. При этом изменение фазы принятого импульса позволяет отслеживать доплеровское смещение частоты для каждого луча в отдельности с помощью когерентной последовательности импульсов.

ПРОХОЖДЕНИЕ КОГЕРЕНТНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

ИМПУЛЬСОВ

ЧЕРЕЗ РАДИОКАНАЛ

Для простоты рассмотрим узкополосные ампли-тудно-модулированные импульсы с несущей частотой ω 0 и амплитудой а ( t ). Импульсы повторяются через промежуток времени T .

Отдельно взятый такой импульс можно представить в виде

u ( t )= a ( t )cos(ω 0 t ).

Когерентная последовательность излученных импульсов (1)

K - 1

f ( t ) = Z a ( t - kT ) cos( ® 0 1 ),                       (2)

k = 0

где K — число импульсов.

Для простоты будем считать, что ω 0 T =2π n , где n — целое число. Тогда спектр последовательности импульсов (2) можно записать как

K - 1

F ( to ) = U ( to ) ^ exp( i to kT ),                     (3)

k = 0

где U (ω)=( A (ω–ω 0 )+ A (ω+ω 0 ))/2, A (ω) — спектр a ( t ). При этом

K - 1

Z exp( i to kT )

k = 0

sin

to TK

to T

sin

Из выражения (4) видно, что сумма экспонент с ростом числа слагаемых стремится к сумме δ-функций. Когерентность последовательности сигналов нужна для того, чтобы экспоненты в сумме не имели сдвигов фаз. В действительности конечная сумма отличается от δ-функции и имеет вид повторяющихся с периодом 2π/ T узких пиков, около которых сгруппированы на небольшом расстоянии более мелкие пики. Таким образом, спектр когерентной последовательности импульсов становится линейчатым. При этом огибающая спектра в окрестности ω=±ω 0 равна спектру отдельного импульса A (ω).

При уменьшении периода повторения импульсов линии спектра раздвигаются, а при увеличении — сближаются.

Когда импульсы начинают сливаться, т. е. период повторения становится меньше или равен длительности отдельного импульса, остается одна линия, если при этом огибающая непрерывного сигнала слабо меняется, то линия превращается в очень резкий пик, соответствующий монохроматическому сигналу. Таким образом, непрерывный квазимонохроматический сигнал можно рассматривать как когерентную последовательность импульсов с периодом повторения меньшим или равным их длительности.

Перейдем к описанию прохождения последовательности импульсов через однолучевой квазиста-ционарный канал, параметры которого медленно меняются со временем. Квазистационарность понимается в том смысле, что такой канал в полосе сигнала в течение времени прохождения k-го импульса можно считать стационарным и характеризовать передаточной функцией

H k ( to ) = H k ( _Ю )| e^{№k ( m )} -

- H 0 k ( 1 + Y o k ( to-to o ) ) е ^{Ф kk} ,

где H 0 _k = | H_k ( to₀)| — модуль передаточной функции на несущей частоте, т _{0 k} = O k ( to ₀) — групповая задержка импульсного сигнала, равная производной фазы передаточной функции по частоте, Y _{0 k} = (ln| H_k ( to ) |)      — логарифмическая произ-

I to=to0

водная модуля передаточной функции по частоте, характеризующая искажения импульса в первом порядке по ширине полосы, Ф _{0 k} = Ф _k ( to ₀) — фаза передаточной функции на несущей частоте, которую мы далее будет называть просто фазой.

Спектр когерентной последовательности импульсов (2), прошедшей через радиоканал, будет иметь вид

F ( to ) = U ( to ) ^ H k ( to )exp( i to kT ).              (6)

k

В случае стационарного канала H _{0 k} = H ₀, τ_{0 k} =τ₀, γ 0 k =γ 0 , Φ 0 k =Φ 0 . Тогда

F ( to ) = U ₀ ( to ) ^ exp( z to kT ).                      (7)

k

Здесь введено обозначение

U 0 ( to ) = U ( to 0 ) H 0 (1 + Y 0 ( to - to 0 )) ./■ ^{+ l T 0} ( ^{to-to 0} ) .

Рассмотрим влияние изменений каждого параметра передаточной функции на принятый сигнал по отдельности.

Для начала рассмотрим изменения фазы. Пусть от импульса к импульсу фаза меняется линейно, т. е. Φ _k =Φ₀+ k ΔΦ. Спектр принятой последовательности в данном случае можно записать

АФ.„

^{F ( to )} = U 0 ^{( to )} ^ exp ^{, (} to + — ) kT .

k

На рис. 1 представлен спектр (8). Здесь и далее спектры представлены без учета огибающей U 0 (ω), по оси абсцисс отложено отклонение от несущей частоты ω 0 , штриховой линией изображен спектр последовательности импульсов в стационарном случае, сплошной — в нестационарном.

Таким образом, видимый сдвиг частоты в принятой последовательности Δω=ΔΦ/ T . Данный сдвиг можно наблюдать на рис. 1.

Теперь рассмотрим влияние сдвига групповой задержки. Пусть групповая задержка также меняется от импульса к импульсу линейно: τ k =τ 0 + k Δτ. Спектр тогда можно записать следующим образом:

F ( to ) = U ₀( to ) ^ exp [ i ( T + AT )( to-to ₀) k ] . (9) k

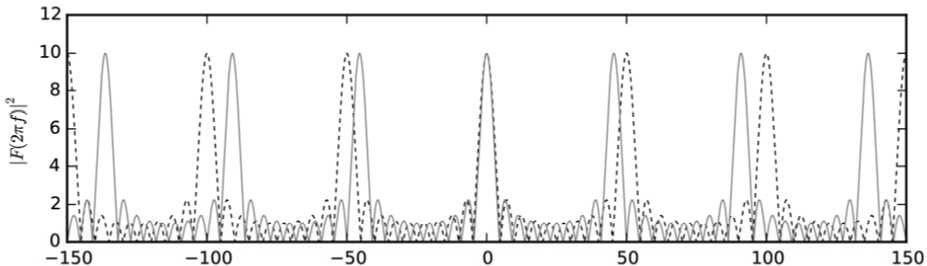
Из (4) и (9) следует, что меняется только расстояние между спектральными линиями, при этом форма и положение спектральной линии, расположенной на ω0, не меняются. Это можно увидеть на рис. 2, на котором изображен спектр (9).

Пусть теперь линейно изменяется амплитуда, H 0k = H 0 +Δ Hk , в этом случае

F ( to ) = U _o ( to)^I 1 + ^{A Hk} I exp( i to kT ).

TI  H0 J

На рис. 3 видно, что малое линейное изменение амплитуды приводит лишь к незначительному уширению спектральной линии, не вызывая сдвига спектральных линий.

И, наконец, рассмотрим влияние γ 0 k =γ 0 +Δγ k :

F(to) = U0(to)S|1 + AY(to-to->k ]x

T ( 1 + Y0(to-to0) J

x exp( i to kT ).

На рис. 4 можно увидеть, что линейное изменение γ 0 также не приводит к сдвигу спектральных пиков, но меняет их форму.

Таким образом, к наблюдаемому сдвигу спектра квазимонохроматического сигнала приводит только изменение со временем фазы передаточной функции. При этом фаза является и самой быстроменя-ющейся величиной.

Многолучевой канал является суммой однолучевых каналов, поэтому передаточная функция также является суммой передаточных функций отдельных лучей.

Пусть имеется несколько лучей, каждый из которых в точке приема можно представить u,(t) = ai cos(to01 + ф) + b sin(to01 + ф). (12)

Их сумма будет иметь вид u (1) = cos(to01)

^ ( a i cos ф , . + b i sin ф , .)

+ sin( to ₀ 1 )

^ ^{( -} a , sin ^ф , + b , cos ^ф , )

Следовательно, в точке приема сигнал является векторной суммой амплитуд отдельных лучей. В стационарном случае имеем чисто гармоническое колебание с некоторой амплитудой и фазой. В нестационарном же случае параметры каждого из лучей непрерывно меняются с течением времени, что приводит к непрерывному изменению их суммы. При этом параметры каждого отдельного луча меняются согласно изменениям параметров среды. Хотя каждый из лучей и является квазимонохроматическим сигналом, их сумма в точке приема будет иметь шумоподобный вид вследствие их интерференции.

При моделировании доплеровского смещения частоты будем учитывать только изменение фазы передаточной функции канала, пренебрегая остальными параметрами. Таким образом, простейший алгоритм измерения доплеровского смещения частоты можно представить следующими шагами:

• 1.    Излучается когерентная импульсная последовательность.

• 2.    В точке приема импульсы разделяются по задержкам и сопоставляются с отдельными каналами.

• 3.    Для каждого импульса определяется его средняя фаза, таким образом получается фазовременная диаграмма для каждого канала.

• 4.    Фазовременная диаграмма переводится в частотно-временную на основании того, что частота — это производная фазы по времени.

  
  
  

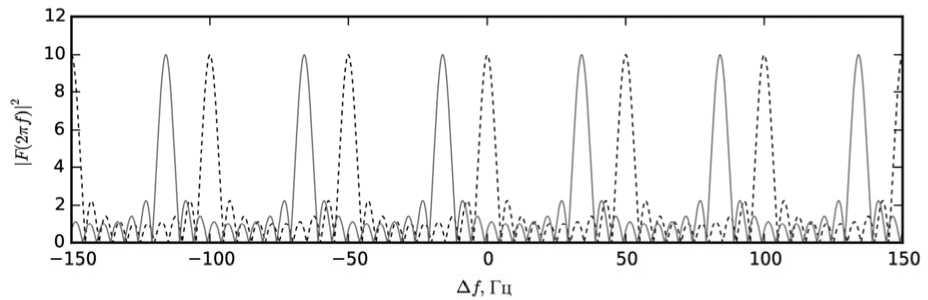
  Рис. 1 . Спектр когерентной последовательности импульсов при линейном изменении Φ ₀

  
  
  

^f, Гц

Рис. 2 . Спектр когерентной последовательности импульсов при линейном изменении τ ₀

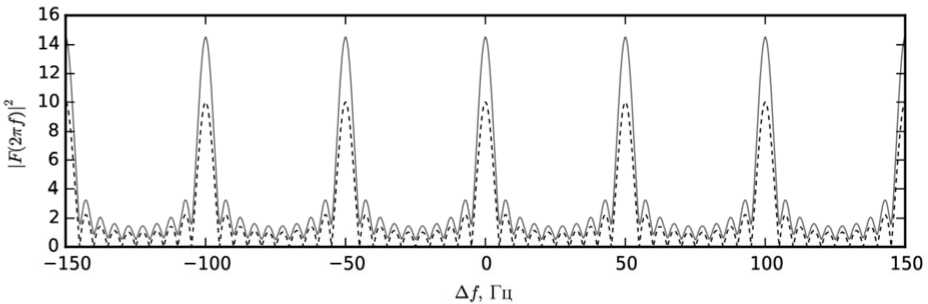
Рис. 3 . Спектр когерентной последовательности импульсов при линейном изменении H ₀

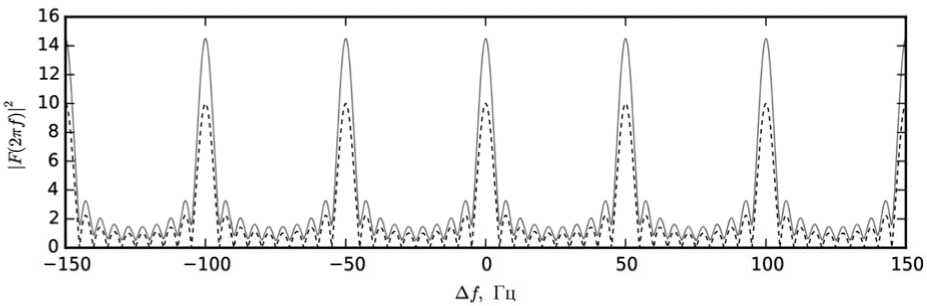
Рис. 4 . Спектр когерентной последовательности импульсов при линейном изменении γ ₀

Следует отметить, что фаза импульса может быть определена с точностью только до 2πn, где n — любое целое число. Для того чтобы сохранить непрерыв- ность и однозначность определения фазы, следует наложить условие, что разница фаз соседних импульсов не может превышать по модулю π. Обычно в ионосферном радиоканале в КВ-диапазоне доплеровский сдвиг частоты не превышает 10 Гц. При условии максимальной разницы фаз между импульсами и максимальной скорости изменения частоты можно получить ограничение на период повторения импульсов T:

T <

2 f _max

где f max — предполагаемый максимальный сдвиг частоты. Для f _max порядка 10 Гц величина T не должна превышать 0.05 с.

МОДЕЛИРОВАНИЕ

Моделирование доплеровского сдвига проводилось на основе метода нормальных волн. В рамках данного подхода (в отличие от геометрического) можно моделировать изменения поля в конкретной точке пространства, что позволяет отслеживать плавные изменения фаз импульсов.

В методе нормальных волн передаточная функция канала [Куркин и др., 1981] может быть записана как

H ( to ) =

= 2 -2 4

ⁿ rr 0    s

9 . . (15)

7In (r0,0) In (r, 9)exP ika Jy n (9) d 9 , где An — системный коэффициент, r0 — высота излучателя, r и θ — координаты приемника, In — коэффициенты возбуждения, a — радиус Земли, k — волновое число, γn — спектральный параметр радиального уравнения.

Для фиксированных точек излучения и приема в случае квазимонохроматического сигнала на несущей частоте ω 0 сумма распадается на несколько сумм, соответствующих геометрооптическим лучам [Потехин, Орлов, 1981], что позволяет воспользоваться терминологией геометрической оптики.

В качестве примера рассмотрим как многолучевой радиоканал ионосферу, нормированный профиль электронной концентрации которой представим в виде двух квазипарабол [Куркин и др., 1981]:

0,

q ( h ) =

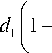
² h b + a ) h + a J

1 - d ₂

h + a

-

h + a

h <  h b .

hь < h < h( hо < h < hm,

где a — радиус Земли, h — высота, hb — высота начала ионосферы, hm — высота максимума, h0 — точка сшивки, а d1 и d2 определяются выражениями d 1 =

d ₂ =

hb + a If hb + a 1--11l-- h0 + a J | hm + a hm + a _ 1 II hm + a hb + a J ( h 0 + a

- i

С течением времени критическая частота меня- ется по закону fcr

= f >cr

1           ( 2 nt) . ( 10n t

1 + a ,cos --- sin ----- f ^ _T J ^ _T

где a f =0.01 и Т =7200 с.

Изменяется также положение точки начала ионосферы:

h b = ^h 0b

1 + 0.5 a_h

л ,       [ 2nt

- 0.5 a_h cos I - T-

где а h =0.000785.

Выбраны следующие начальные значения параметров ионосферы: высота нижней границы ионосферы — 90 км, точка сшивки — 195 км, высота максимума — 300 км, критическая частота — 6 МГц. Через данный радиоканал была пропущена последовательность когерентных импульсов с частотой несущего сигнала 10 МГц, длительность одного импульса — 120 мкс. Расстояние между точками излучения и приема — 3500 км.

В каждый момент времени моделировалось прохождение одного импульса через ионосферный радиоканал. В точке приема, после демодуляции, импульсы разделялись по задержкам и для каждого импульса находились средние амплитуда и фаза. Период повторения импульсов был выбран 0.05 с.

Фазы отдельно взятых лучей, полученные в результате моделирования прохождения когерентной последовательности импульсов через ионосферный радиоканал, представлены на рис. 5. В точку приема приходят четыре луча: два двухскачковых и два трехскачковых. Видно, что нижние лучи более чувствительны к изменениям параметров нижней части ионосферы, где лежат их области отражения. В то же время верхние лучи более чувствительны к изменениям характеристик верхней части ионосферы (в данном случае к изменению критической частоты). При этом в обоих случаях более чувствительными оказываются двухскачковые лучи. Такое поведение хорошо согласуется с физическим представлением процесса.

Доплеровское смещение частоты определяется как скорость изменения фазы (рис. 6). Таким образом, мы можем наблюдать тонкую структуру доплеровского смещения частоты в зависимости от изменения параметров среды.

Результаты моделирования прохождения непрерывного квазимонохроматического сигнала частотой 10 МГц представлены на рис. 7. Из-за сильной интерференции и малости частотных сдвигов определение доплеровского смещения отдельно взятого луча в общем случае, как упоминалось выше, не всегда возможно.

ЗАКЛЮЧЕНИЕ

Рассмотрен метод измерения доплеровского смещения частоты в многолучевых радиоканалах для каждого луча в отдельности с помощью когерентной последовательности импульсов, позволяющий отслеживать детально изменения параметров радиоканала (тонкую структуру).

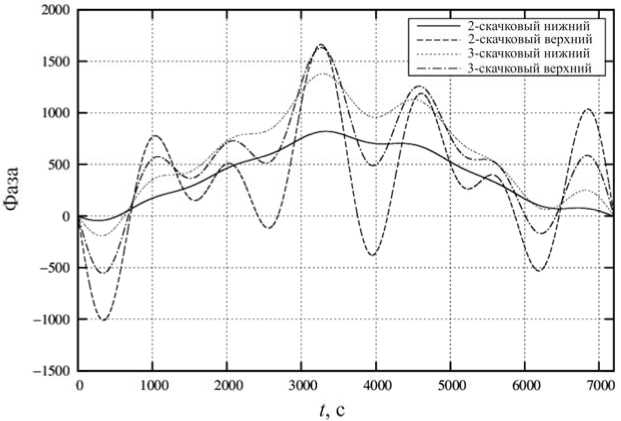
Рис. 5 . Фазы отдельных импульсов

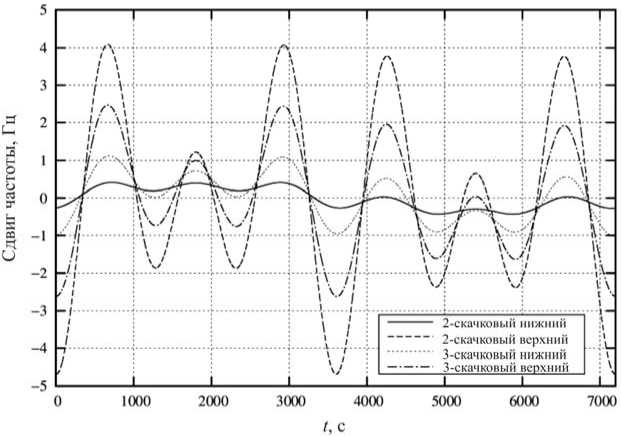
Рис. 6 . Доплеровское смещение частоты отдельных импульсов

Амплитуда              Амплитуда              Амплитуда

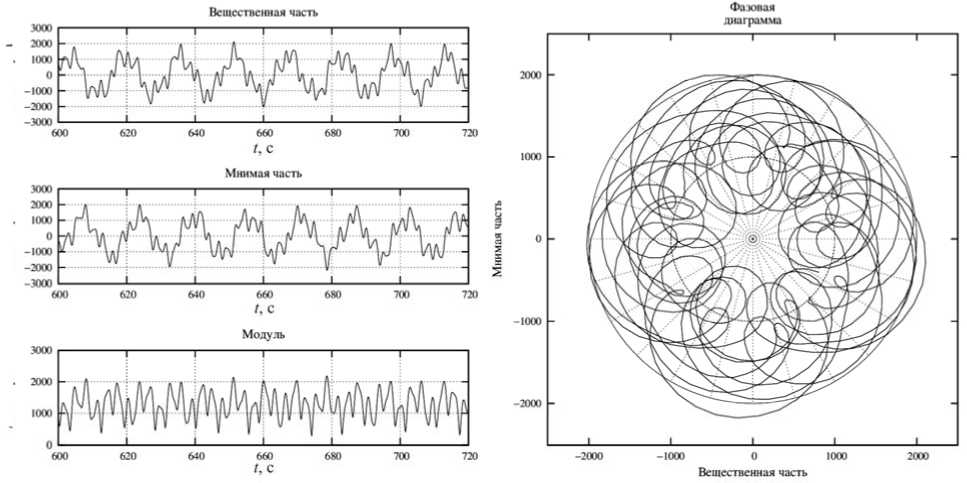
Рис. 7 . Непрерывный сигнал

Показано, что наибольший вклад в доплеровское смещение частоты вносит изменение фазы передаточной функции канала.

На основе рассмотренного метода было проведено моделирование распространения когерентной импульсной последовательности в простейшем случае плоскослоистой ионосферы с медленно меняющимися с течением времени параметрами. Результаты моделирования показывают, что на изменение характеристик отдельного луча влияют вариации параметров ионосферы в областях отражения, что качественно соотносится с экспериментальными данными.

Таким образом, если имеется модель динамики ионосферы, то можно анализировать поведение фаз и амплитуды лучей по отдельности. При этом на изменение параметров луча фактически будут влиять только вариации параметров ионосферы в областях отражения. На основе этого можно определить характер изменения доплеровского смещения частоты и попытаться выяснить, существуют ли какие-либо особенности в проявлении эффекта Доплера, характерного для данной модели динамики ионосферы.

Работа выполнена при финансовой поддержке РФФИ (№ 13-05-00979-а).