Моделирование движения танкера на нефтяном терминале в открытом море при управлении на перекрестии

Процесс моделирования сложного маневрирования танкера на перекрестии во время выполнения операций по погрузке нефти и нефтепродуктов на терминале, находящемся в открытом море, реализуется с использованием математически идентифицированной модели танкера.

2.    Реализация моделирования

Проведем ряд модельных испытаний функционирующей системы управления по двум парам отклонений от ортогональной системы координат. Будем перемещать само перекрестие, а с ним и систему координат. Данная стратегия управления сложнее маневрирования на терминале, но служит хорошей демонстрацией возможностей моделирующей системы.

Пусть цель-перекрестие движется в заданном направлении (330°) с заданной скоростью (0.3 уз). Начальная скорость танкера 0.5 уз, курс 60°. Наблюдение за танкером ведется на протяжении 6 000 с. Параметры системы управления маневрированием а 1 , а 2 и а 3 указаны:

• –    в законе управления упором главного движителя:

Тe = (kWномP%/ v)A, где А = 1 / (а3Lw); Р% – процент загрузки главного движителя;

• –    законе управления тягами подруливающих устройств:

ТeprF = [ a ₂ ( d_yA – d_yF ) + a ₁ ( d_yA + d_yF ) xA ] /( xF – xA ),

ТeprA = [– a ₂ ( d_yA – d_yF ) + a ₁ ( d_yA + d_yF ) xF ] /( xF – xA ), где a 1 = –25; a 2 = 2250.

Данные параметры можно изменять и тем самым подбирать их оптимальные значения, способствующие достижению минимального уровня качества управления:

t

Q ¹    r ² dt .

t ₀

Разработанная программа моделирования позволяет детально проследить за изменением всех характеристик маневрирования (рис. 1). На траектории танкера синим кружком обозначен сам танкер, цветная прямая отражает линию движения цели, красный кружок – перекрестие. Скриншот получен на 1 325 с маневрирования; на нем видно начальное значительное отклонение от цели, которое затем убывает в процессе управления танкером.

Покажем изменения всех сопутствующих движению параметров:

• –    тяги T_e и процента загрузки P % главного движителя (рис. 2);

• –    курса т, угловой скорости (О и угла дрейфа ₽ (рис. 3);

• –    тяги носового TeprF и кормового TeprA ПУ и их результирующего момента Mpr (рис. 4);

• –    продольной ( v_x ) и поперечной ( v_y ) скорости и отклонений носовой ( d_xF , d_yF ) и кормовой ( d_xA , d_yA ) точек ( Юдин и др. , 2013) от координатных осей перекрестия (рис. 5).

Петров С.О. и др. Моделирование движения танкера…

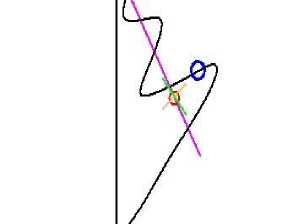
Рис. 1. Траектория движения танкера при управлении на перекрестии. Перекрестие движется линейно

Для всех показателей характерны периодические изменения с постепенным уменьшением амплитуд колебаний. В итоге наблюдаются примерно стационарные колебания, которые вызваны естественным перерегулированием параметров а ₁ , а ₂ и а ₃ , указанных в таблице.

а 1	а 2	а 3	Q
–25	2 000	50	0.0118
–25	3 000	50	0.0113
–20	3 000	50	0.0108
–20	2 000	50	0.0122
–15	3 500	50	0.0112
–18	3 300	50	0.0108
–18	3 300	30	0.0110
–18	3 300	70	0.0105

Для оптимизации управления меняем в программной форме (рис. 6) значения параметров а 1 , а 2 , а 3 и каждый раз запускаем процесс выполнения маневрирования. После завершения испытаний запрашиваем качество управления Q и фиксируем его в таблице. В ходе простого сравнения перебранных комплексов трех параметров выбираем заключительный вариант: а 1 = –18, а 2 = 3300, а 3 = 70. Эта комбинация параметров показывает минимальное значение качества управления Q = 0.0105.

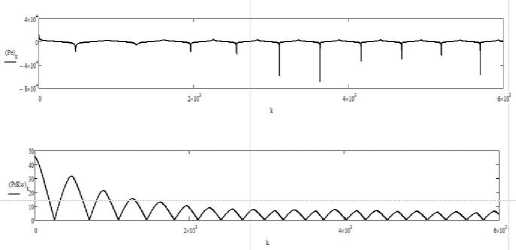
Рис. 2. Изменение тяги и процента загрузки главного движителя. Движение цели линейное

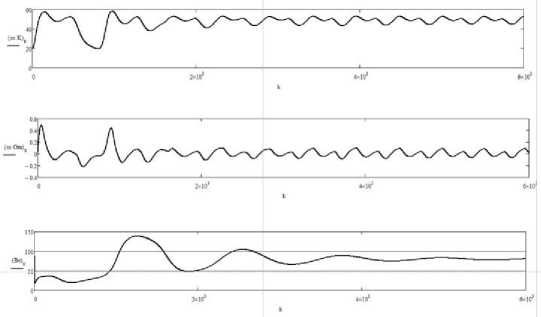
Рис. 3. Изменение курса, град, угловой скорости, град/с, и угла дрейфа, град. Движение цели линейное

Вестник МГТУ, том 18, № 1, 2015 г.    стр. 25-32

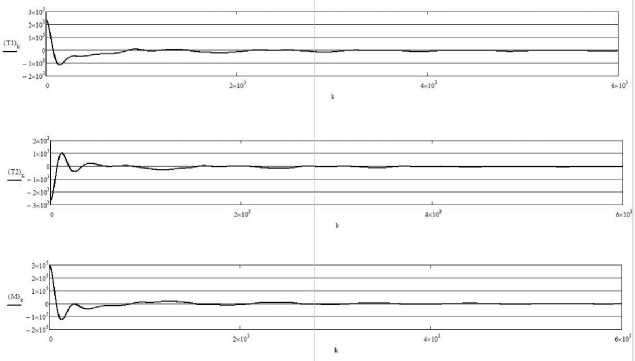
Рис. 4. Изменение тяги носового и кормового ПУ, кН, и их результирующего момента, кНм. Движение цели линейное

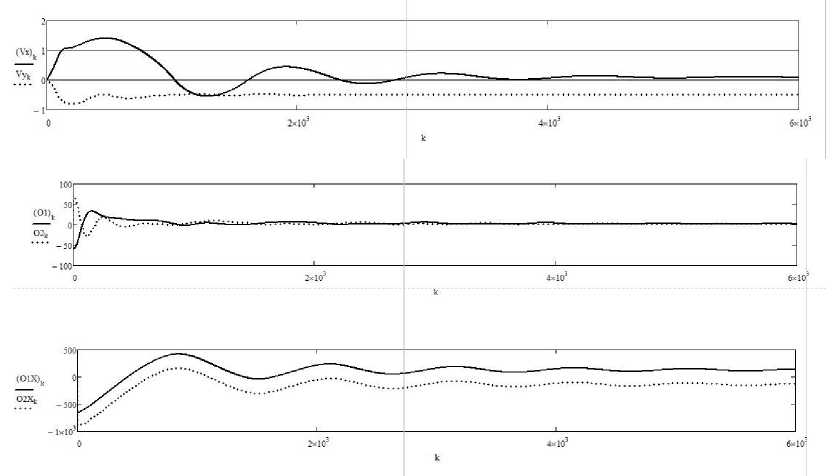
Рис. 5. Изменение продольной и поперечной скоростей танкера, м/с, отклонений его носовой и кормовой точек, м, от координатных осей перекрестия. Движение цели линейное

ТРОС

Якорь

Буксировка

Поворот 1

Поворот 2

КЬ

Т ерминал

Г" Нет Буксиров

Г НЕТ ТРОСА

{v Есть Подкод

V Есть подруль!

v Есть подруль2

120 т¥

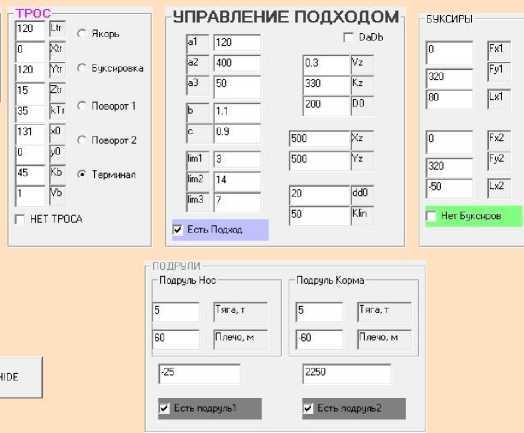
Рис. 6. Часть программной формы для задания параметров управления

УПРАВЛЕНИЕ

а1	120
а2	400
аЗ	50
Ь	1.1

ПОДХОДОМ

0.3	Vz
330	Kz
200	DO

Г-ПОДРУЛИ

П одру ль Нос		Подру ль Корма
5	|Тяга,т	5	|Тяга,т
60	|Плечо, м	60	|Плечо, м

Петров С.О. и др. Моделирование движения танкера…

Траектория маневрирования изменяется незначительно, что способствует небольшому изменению качества управления Q ( Юдин , Пашенцев , 2012). На рис. 7 показаны траектории, соответствующие трем различным комбинациям управляющих параметров (обозначения те же, что и на рис. 1).

Линейно удаляющаяся цель-перекрестие не имеет прямого отношения к задаче маневрирования танкера на терминале, но показывает возможности предложенного способа управления и мощность программной системы моделирования.

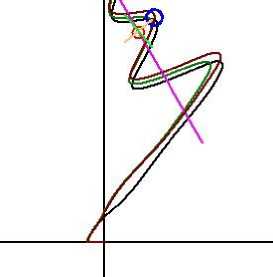
Рис. 7. Изменения траектории при вариации параметров управления

Рассмотрим задачу моделирования процесса маневрирования танкера, когда цель совершает колебательные движения вокруг неподвижной точки.

Аналитически данное движение представим в виде

X z = A sin(2 π t / T 1 ), Y z = B cos(2 π t / T 2 ).

Графические траектории такого движения являются фигурами Лиссажу и при разных комбинациях амплитуд А , В и периодов Т ₁ , Т ₂ могут быть весьма причудливыми. Приведем результаты модельных испытаний двух случаев маневрирования с одинаковыми амплитудами, равными 5 и 12 м, и на порядок отличающимися частотами. В первом испытании учитывались периоды Т ₁ = 10 c, Т ₂ = 6 с, во втором – Т 1 = 100 с, Т 2 = 60 с. Заметим, что система управления выполнила в обоих случаях главную задачу – не уходить от центра колебаний, однако частотные характеристики основных параметров маневрирования при этом различны, как это и должно быть по существу задачи. Ниже приведем в графической форме те же характеристики маневрирования, которые представлены на рис. 1-5. Так, на рис. 8-12 приведены результаты для периодов колебания цели Т 1 = 10 с, Т 2 = 6 с, на рис. 13-17 – результаты для периодов Т ₁ = 100 с, Т ₂ = 60 с.

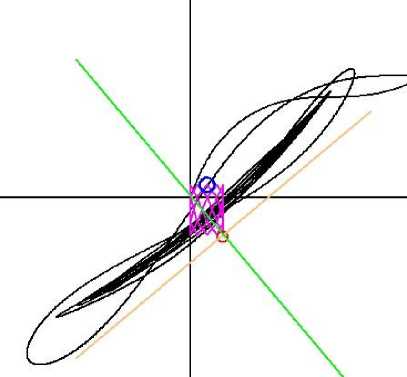
Рис. 8. Траектория управляемого танкера при движении на перекрестии, колеблющемся с осевыми периодами Т ₁ = 10 с, Т ₂ = 6 с ( Q ₁ = 0.0137)

Движения перекрестия-цели быстрые, так как периоды осевых колебаний малы. Особо следует обратить внимание на изменение угла дрейфа танкера (рис. 10, внизу). Дело в том, что при выбранной системе управления часть времени маневрирования танкер движется задним ходом, что приводит к

Вестник МГТУ, том 18, № 1, 2015 г.    стр. 25-32

изменению угла дрейфа почти на 180°. Именно это обстоятельство отражают вертикальные линии на графиках угла дрейфа. Как известно, любое судно, тем более тяжелый танкер, является фильтром высоких частот. Поэтому курс и угловая скорость (рис. 10) затухают со временем после начального переходного процесса.

Эффект фильтрации виден и на примере качества управления. Так, при высокочастотном режиме Q 1 = 0.0137, а при низкочастотном – Q 2 = 0.0425. Система управления не реагировала на малые высокочастотные отклонения, что и привело к хорошему показателю качества ( Q 1 существенно меньше Q 2 ).

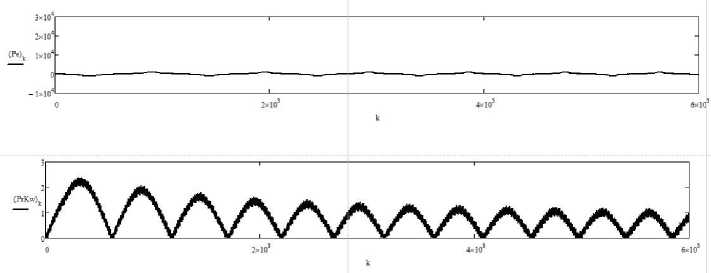
Рис. 9. Изменение тяги и процента загрузки главного движителя. Перекрестие цели колеблется с осевыми периодами Т ₁ = 10 с, Т ₂ = 6 с

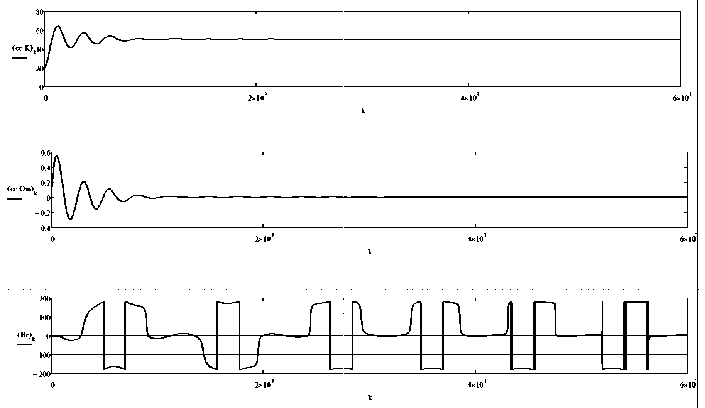
Рис. 10. Изменение курса, угловой скорости и угла дрейфа танкера. Перекрестие цели колеблется с осевыми периодами Т 1 = 10 c, Т 2 = 6 с

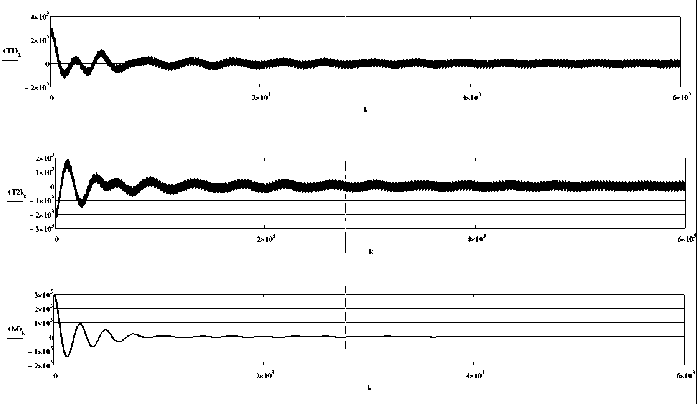
Рис. 11. Изменение тяг носового и кормового ПУ и их результирующего момента. Перекрестие цели колеблется с осевыми периодами Т 1 = 10 c, Т 2 = 6 с

Петров С.О. и др. Моделирование движения танкера…

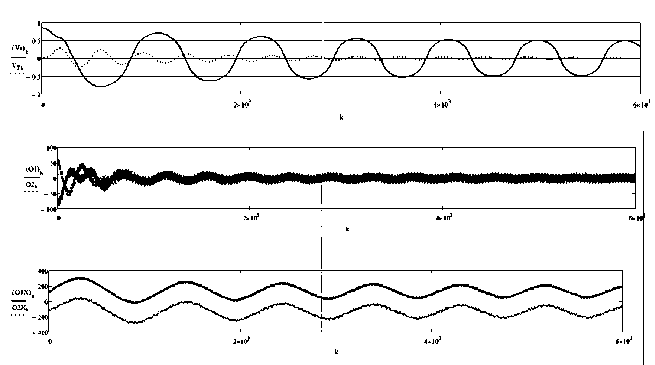
Рис. 12. Изменение продольной и поперечной скоростей танкера и отклонений его носовой и кормовой точек от координатных осей перекрестия.

Перекрестие цели колеблется с осевыми периодами Т 1 = 10 c, Т 2 = 6 с

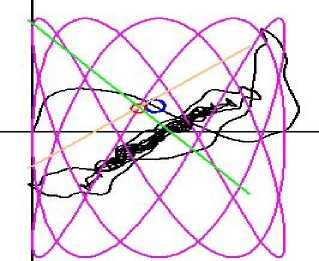
Рис. 13. Траектория движения танкера при управлении на перекрестии. Перекрестие колеблется с осевыми периодами Т 1 = 100 c, Т 2 = 60 с ( Q 1 = 0.0425).

Движения цели-перекрестия медленные, так как периоды значительны

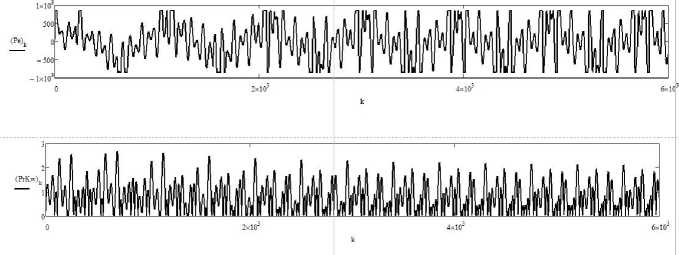
Рис. 14. Изменение тяги и процента загрузки главного движителя. Перекрестие цели колеблется с осевыми частотами Т ₁ = 100 с, Т ₂ = 60 с

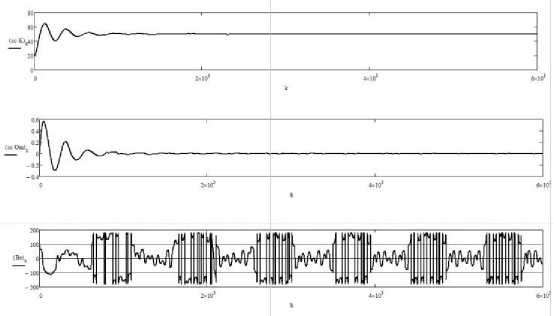
Рис. 15. Изменение курса, угловой скорости и угла дрейфа танкера. Перекрестие цели колеблется с осевыми периодами Т 1 = 100 c, Т 2 = 60 с

Вестник МГТУ, том 18, № 1, 2015 г.    стр. 25-32

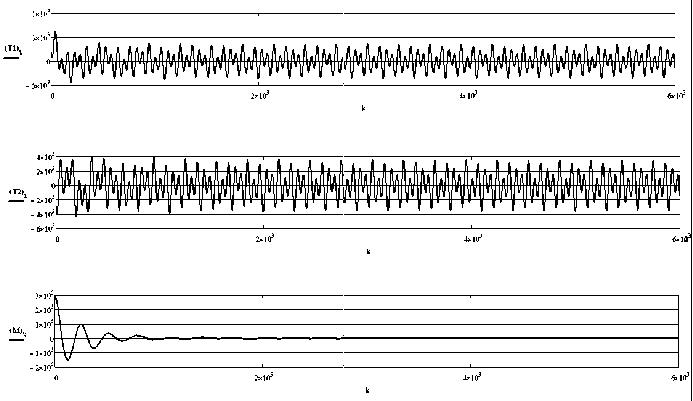
Рис. 16. Изменение тяг носового и кормового ПУ и их результирующего момента. Перекрестие цели колеблется с осевыми периодами Т ₁ = 100 c, Т ₂ = 60 с

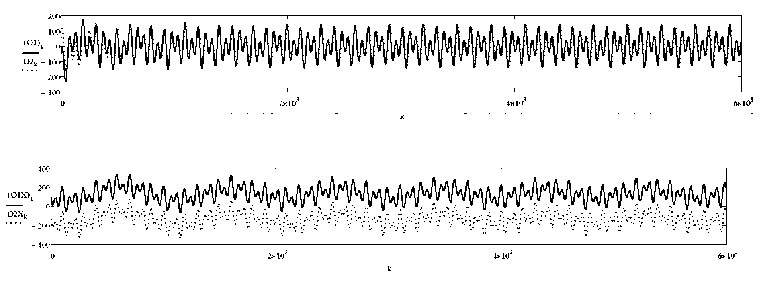
Рис. 17. Изменение продольной и поперечной скоростей танкера и отклонений его носовой и кормовой точек от координатных осей перекрестия.

Перекрестие цели колеблется с осевыми периодами Т ₁ = 100 c, Т ₂ = 60 с

3.    Заключение

В статье показан процесс моделирования инновационной стратегии управления движением танкера на перекрестии во время выполнения операций по погрузке нефти и нефтепродуктов на терминале, находящемся в открытом море. Моделирование осуществлялось с целью решения задач сложного маневрирования с использованием параметрически идентифицированной математической модели танкера.