Моделирование движения жидкости в прецизионном дозаторе

Политов Евгений Николаевич, кандидат технических наук, доцент поступательное движение под действием силы FЭ – управляющего электромагнита, кусочнолинейной силы упругости Рупр, возникающей за счет действия возвратной пружины, жесткостью с, силы сухого трения F(х) и силы вязкого сопротивления R(:x) = ^x , вызванной наличием гидравлического сопротивления жидкой среды. За обобщенную координату х примем перемещение массы m.

а)                                       б)

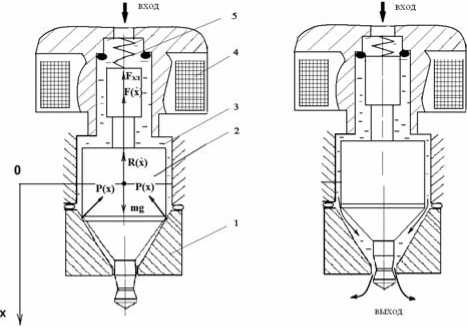
Рис. 1. Расчетная схема электромагнитного дозатора:

а – закрытое состояние дозатора; б – открытое состояние дозатора; 1 – седло клапана, 2 – запирающий элемент, массой m, 3 – дозируемая жидкость; 4 – обмотки электромагнита; 5 – возвратная пружина

На рис. 2 показана развертка распределенной реакции, действующей на исполнительный элемент со стороны седла клапана. В расчетах эта нагрузка заменена приведенной сосредоточенной силой Р(х) на участке кольцевого зазора, развертку которого на плоскости можно представить отрезком, длинной l и распределенной нагрузкой, интенсивностью р(х), где P(x) = j p ( x ) dL .

L

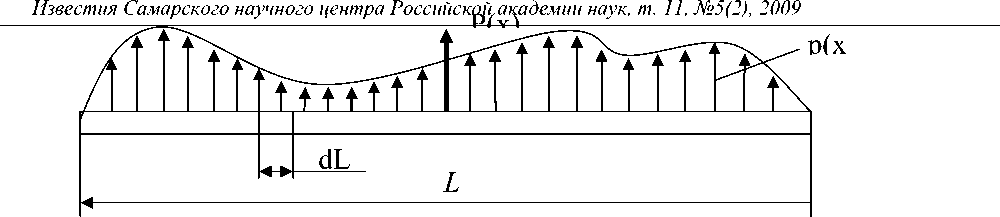
Рис. 2. Развертка распределенной реакции, действующей на исполнительный элемент со стороны седла клапана

Для описания динамических процессов, протекающих в рассматриваемой системе, записаны соответствующие нелинейные дифференциальные уравнения:

mx + px + P(x)+ F(x) = —Fy

Данную модель аналитически можно представить в виде:

Fsign(x),

F(X) = b Fo,

dÔ

— +

dt

^Э-R = U(t) z2μ0s

— Fsign(F o ),

X * 0;

X = O,|F o l < F;

X = O,|F o | > F.

•     • • где х,х,х

— соответственно обобщенная ко-

ордината, скорость, ускорение; μ – коэффициент вязкого трения; m – масса клапана; Р(х) – кусочно-линейная сила упругого сопротивления; F( х ) – сила сухого трения; U(t) – напряжение электрического питания; R – активное сопротивление катушки электромагнита, F Э – электромагнитная сила, Ф – магнитный поток; µ 0 – магнитная проницаемость; s= πd² – площадь поперечного сечения кольцевого зазора, z – число витков проводника с током.

Закон движения иглы клапана зависит от параметров упруго-диссипативных элементов клапана с параметрами упругости с, вязкости ц , а также действующих сил со стороны упругих ограничителей с параметрами с 1 , с 2 . В качестве модели сухого трения принята модель, описанная в [4]. На графике, приведенном на рис. 3, представлена зависимость силы трения от скорости

где F ^{+ ,F} - предельная сила сухого трения; F 0 – равнодействующая всех сил, кроме силы сухого трения, x & – скорость вдоль оси Ох.

К внутренним силам, действующим в рассматриваемой системе, относятся сила упругости Р упр и сила вязкого сопротивления F _всопр [5]. Сила упругости в данной системе кусочно-линейна. На рис. 4 представлена зависимость силы упругости от обобщенной коорднаты:

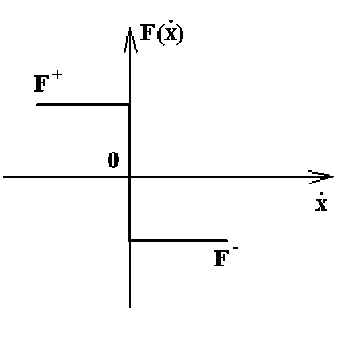
Рис. 3. Модель силы сухого трения

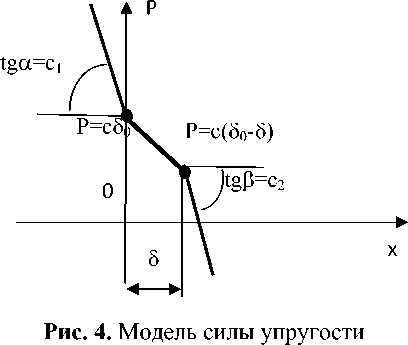
Модель упругого сопротивления

аналитически можно представить в

следующем виде:

Р ( х Н

^{с ( 5} 0 ^{— х} )

— C i x + с § о

— с 2 (х — 5)+с(^0 — 5)

при при при

0 < х < 5

х <  0

x > 5

где: 5 - рабочий зазор электромагнита; 5₀ -величина поджатия пружины; с - коэффициент жесткости пружины; с 1 , с 2 – параметры вязкоупругих ограничителей.

Электромагнитная сила, приближенно может быть определена по формуле 4 [4]:

Ф ²

^F      ^2

ц ₀ п d

.

Система уравнений (1) решается с учетом (2), (3), (4) численным методом с использованием оригинального алгоритма в среде Mathcad 2000, результаты моделирования представлены на рисунках 5, 6.

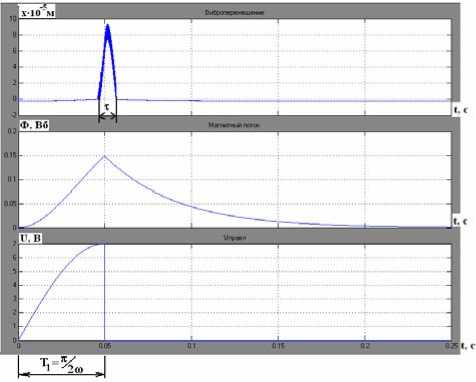
Рис. 5. График перемещения и потока при синусоидальном импульсе, частотой 5 Гц: τ - время отрыва клапана от седла

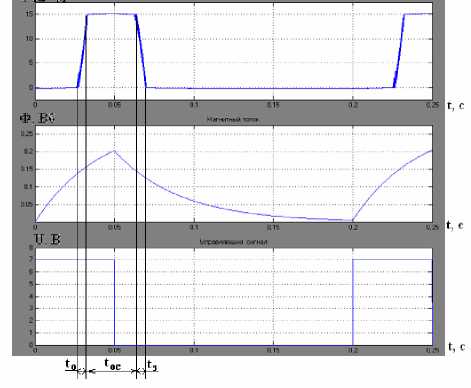
Рис. 6. График перемещения и потока при прямоугольном сигнале, скважность 25%, частота импульсов 5 Гц, t 0 , t з – фаза открытия и закрытия клапана, t ос – фаза открытого состояния клапана дозатора

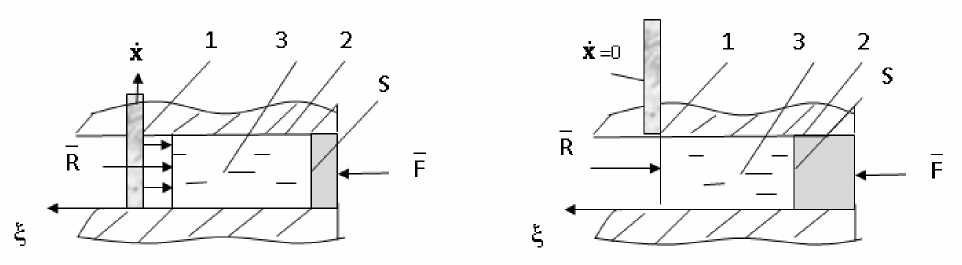
Расчет объема единичной дозы дозатора. В качестве расчетной схемы движения жидкости в дозаторе примем модель, представленную на рис. 7. Будем считать, что жидкость несжимаема, запирающий элемент открывается мгновенно, а жидкость в момент открытия имеет нулевую скорость и начинает двигаться как твердое тело на которое действует сила F и сила вязкого сопротивления R = у^ , вызванная наличием гидравлического сопротивления жидкой среды, где v - эмпирический коэффициент гидравлического сопротивления дозатора.

а)                                                                       б)

Рис. 7. Приведенная расчетная схема движения жидкости в дозаторе:

1 – запирающий элемент; 2 – упрощенная модель канала системы подачи жидкости; 3 – дозируемая жидкость

Для описания динамических процессов, протекающих в рассматриваемой системе, запишем дифференциальное уравнение движения жидкости, при начальных условиях t=0; ^ =0;

dV

= - 2 nV + f ; dt

• •       ——    __

m! = -R+F;

v    F   pS   p

где 2n = —; f = — =---= —;

m    m S p L p L

Известия Самарского научного центра Российской академии наук, т. 11, №5(2), 2009

S - площадь сечения отверстия; р , V , р -давление, скорость и плотность потока жидкости соответственно.

Обозначим: U = –2nV + f, , тогда для f=const dU     dV

---= - 2 n ;

dt        dt

Если запирающий элемент открыт в течении времени Т, то объем дозы Q найдем по формуле:

T Q = q ( t ) dt ;

После преобразований получим:

Преобразуем (6) c учетом (7), тогда:

dU dt dU U

• - 2 nU ;

• - 2 ndt ;

Q = pS- T + pS- e "^{2 nT} ;            (12)

v     2 nv

v

Пусть Я =    ; тогда

Интегрируя уравнение (6) с учетом (7), (8), (9) найдем закон изменения скорости:

V = ^— ( 1 - e ^{2 nt} ) или

2 n

Q = p x

( T XS_T к

T + ^P Le ^{p L}

X S

к

j

V=

-

2 n p L

- 2 nt e

) v = pS v

к

1 - e^spL к

; (10)

J

Тогда объемный расход [3] определим как q = VS

q =

pS ² v

v

1 - e^spL

к J

Таким образом, объем дозы пропорционален давлению жидкости р и обратно пропорционален коэффициенту гидравлического сопротивления дозатора v , а также нелинейно зависит от времени открытия Т. На рис. 8 показан график зависимости расхода жидкости от времени для различных коэффициентов гидравлического сопротивления дозаторов.

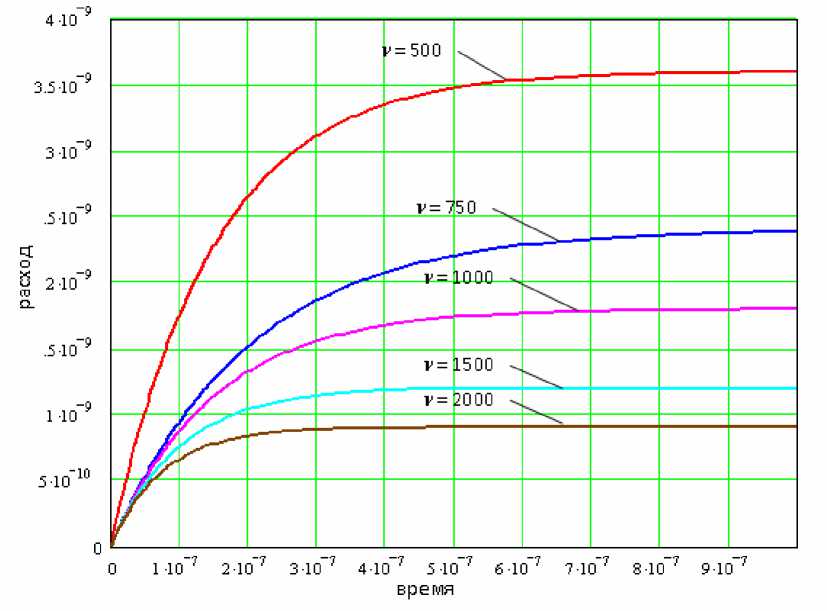
Рис. 8. График зависимостей расхода жидкости от времени для различных дозаторов

Выводы: построена математическая модель и получены дифференциальные уравнения, описывающие движение исполнительного органа прецизионного дозатора, разработана методика их решения в нестационарном режиме и выявлена функциональная связь между параметрами свойств системы и расходом жидкости, видом электрического питания электромагнитов для различных физических свойств жидкости, позволяющая определять параметрами дозатора.

Работа выполнена в рамках госконтракта П2144 от 05.11.09.