Моделирование двойниковых межзеренных границ в оцк металлах и сплавах

В связи с колосальным развитием вычислительных систем растет популярность применения так называемого вычислительного эксперимента в тех научных направлениях, в которых экспериментальные исследования и непосредственные измерения весьма затруднены, а иногда – невозможны. К одному из таких направлений относятся исследования на микро-, нано- и мезомасштабах, для которых широко применяется атомистическое моделирование: моделирование методом Монте-Карло, молекулярно-динамическое моделирование, расчеты из первых принципов ( Ab Initio ).

В силу того, что реальным твердым телам присуще огромное множество дефектов и несовершенств кристаллической структуры, несомненный интерес для исследователя представляют процессы, происходящие с участием таких образований. С экспериментальной точки зрения сдерживающим фактором здесь является с одной стороны скоротечность таких процессов, с другой – достаточно малые размеры.

Данная работа посвящена исследованию протяженных, линейных дефектов кристаллической решетки, таких как специальные межзеренные границы. Исследование проведено методом молекулярной динамики.

2.    МОДЕЛЬ МЕЖЗЕРЕННОЙ ГРАНИЦЫ

границы зерен (ГЗ, GB), представляют собой монокристаллические области, структуры которых связаны друг с другом операцией точечной симметрии. Специальная ГЗ представляет собой границу между двойниками, являясь плоскостью зеркальной симметрии. Такие дефекты нарушают трансляционную инвариантность в направлении, перпендикулярном плоскости распространения ГЗ, однако в направлениях параллельных ГЗ трансляционная симметрия сохраняется.

В работе рассматриваются следующие мете-риалы, имеющие объемо-центрированную кубическую (ОЦК) кристаллическую решетку: аль-фа-железо, хром, ванадий и неупорядоченный бинарный сплав Fe-10ат. % Cr. Для каждого из этих материалов рассмотрены шесть типов двойниковых ГЗ, перечисленных в табл. 1.

Для некоторых типов ГЗ начальная (неотре-лаксированная) атомная конфигурация бикристаллита обладает относительно высокой потенциальной энергией, в силу малых расстояний между атомами монокристаллитов на границе раздела. Для исключения таких областей существует два способа: первый из них основан на поиске наименьшего энергетического состояния обоих монокристаллтов путем смещения одного относительно другого в направлении распространения ГЗ [1], второй – на замене близко лежащих атомов граничащих двойников одним атомом, лежащим на границе раздела.

При использовании первого из описанных способов нарушается пространственная зеркальная симметрия относительно плоскости распространения ГЗ, при применении второго способа уменьшается число частиц в моделируемой системе. В данной работе в качестве метода построения структур с ГЗ выбран второй из описанных

Таб. 1. Параметры исследуемых типов симметрично-наклонных межзеренных границ

Тип границы зерна	Ось вращения	Угол наклона од ного зерна относительно другого a , о
(320)[001] ∑ 13	[001]	22.62
(530)[001] ∑ 17		28.07
(210)[001] ∑ 5		36.87
(310)[001] ∑ 5		53.13
(410)[001] ∑ 17		61.93
(510)[001] ∑ 13		67.38

У5 (310)[0011

Рис. 1. Фрагменты неотрелаксированных ОЦК бикристаллитов с межзеренными границами (окружностями серого и черного цветов отображены атомы, находящиеся в смежных атомных слоях)

выше методов. Фрагменты начальных ОЦК бикристаллитов изображены на рис. 1.

Как отмечалось выше, наличие в микрокристаллите специальной ГЗ нарушает трансляционную симметрию в одном из направлений. Поэтому моделирование требует применения специальных граничных условий (ГУ), которые с одной стороны должны имитировать «бесконечную» структуру, с другой – воспроизводить одиночную протяженную ГЗ. В качестве таких граничных условий применяются смешанные ГУ: атомы, лежащие на границах, параллельных плоскости распространения ГЗ, закрепляются в своих первоначальных по- ложениях; для границ, перпендикулярных ГЗ, используются периодические ГУ.

3.    МОДЕЛИРОВАНИЕРЕЛАКСАЦИИ БИКРИСТАЛЛОВ

Все типы симметрично-наклонных межзеренных границ по отдельности моделировались в трех металлах a -Fe, Cr, V и неупорядоченном бинарном сплаве Fe-10 % ат.Cr при температуре 300 K. Время релаксации бикристаллитов составляло около 30 пс. Выбранного временного промежутка достаточно для достижения системой энергетически выгодной атомной конфигурации. Линейные размеры бикристаллитов выбирались таким образом, чтобы максимально уменьшить влияние жестких граничных условий и составили 230, 170 и 170 Д3 вдоль осей OX, OY и OZ соответственно.

Межатомное взаимодействие для всех систем было описано в рамках метода погруженного атома (МПА, EAM) [2, 3]. Для a -Fe был использован многочастичный потенциал, разработанный Акландом, Менделеевым и др. [4] (модификация ранее разработанного потенциала [5]), для хрома использован потенциал из работы [3], для ванадия – из работы [6]. Потенциал для описания кросс-взаимодействия между железом и хромом для сплава Fe-10ат. % Cr взят из работы [7].

Моделирование проведено на вычислительном кластере Научно-исследовательского технологического института УлГУ (НИТИ УлГУ) с применением молекулярно-динамического пакета MDRDS, также разработанным в НИТИ УлГУ.

4.    РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Существенные изменения в энергии системы происходят в течение нескольких десятков временных шагов, по истечении которых устанавливается равновесная атомная конфигурация, в соответствие с заданной температурой. В приграничной области ГЗ происходит формирование так называемой межзеренной (зернограничной) области, отличающейся своим энергетическим и пространственным состоянием от областей, лежащих в объеме монокристаллитов, для которых характерно сохранение ОЦК структуры в течение всего времени моделирования (рис. 2). Как хорошо видно из рис. 5 для зернограничной области характерен ощутимый «всплеск» потенциальной энергии, имеющий, между тем, множество локальных потенциальных «ям». Ширина межзеренных областей достаточно мала по сравнению с размерами бикристаллитов.

Энергия двойниковой ГЗ E_GB может быть определена как избыточная энергия микроструктуры, локализованная в межзеренной области [8]:

Е

GB

E p "  N • E s

S

где Ep – полная потенциальная энергия релаксированного бикристалла, N – число частиц, находящееся в расчетной области, Es – энергия связи, приходящаяся на один атом бездефектной кристаллической решетки монокристаллита, S – площадь границы зерна.

Соответствующие результаты определения удельных энергий межзеренных границ представлены на рис. 3. Оценки удельной энергии двойниковых границ лежат в интервале 0,054 – 0,087 eV/ Д ² для всех рассмотренных материалов. Среди чистых металлов наибольшими значениями удельной энергии обладают ГЗ в ванадии, наименьшими – ГЗ в альфа-железе. Моделирование показало, что процесс релаксации для

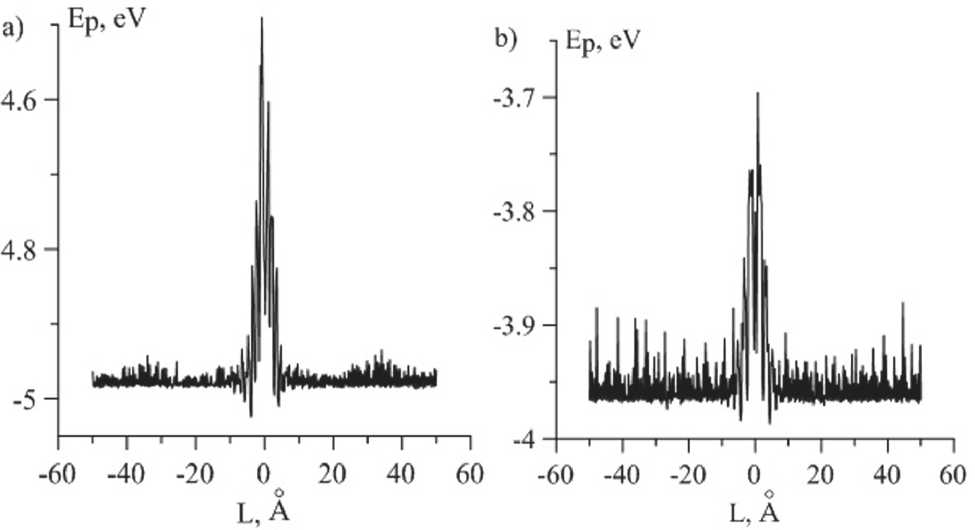
Рис. 2. Распределение потенциальной энергии бикристаллита (на один атом) вдоль направления, перпендикулярного плоскости распространения ГЗ:

a – (510)[001] ∑ 13 в ванадии; b – (210)[001] ∑ 5 в сплаве Fe-10ат.Cr (Начало отсчета на оси абсцисс совпадает с плоскостью распространения ГЗ)

Egb, ev/A²

■ Pure V

0,084 -

0,074 -

0,064-

0,054

i

A

PureCr

OPureFe

△ Fe-10at.%Cr

i

*

О

41   9» °

Рис. 3. Удельная энергия межзеренных границ в чистых металлах в зависимости от угла разориентации двойников в бикристаллите различных ОЦК систем проходит неоднозначно. Так для ванадия максимальной зернограничной энергией обладает ГЗ (410)[001] ∑ 17, минимальной – (210)[001]∑5. Как для хрома, так и для альфа-железа наибольшим значением энергии обладает ГЗ (530)[001]∑ 17, наименьшим – (310)[001]∑5. Стоит отметить, что ранее бикристаллиты ванадия были рассмотрены группой исследователей в работе [9] при 10 К. Результаты изменения удельной межзеренной энергии в зависимости от угла разориентации двойников [9] качественно совпадают с результатами, полученными в данной работе.

Для неупорядоченного сплава Fe-10ат.Cr значения удельной энергии ГЗ на графике лежат в непосредственной близости от соответствующих оценок, полученных для чистого альфа-железа.

5.    ЗАКЛЮЧЕНИЕ

В работе предложена атомарная модель протяженных двойниковых ГЗ для металлов с ОЦК структурой. Модель основана на многочастичном межатомном взаимодействии в формализме метода погруженного атома. Методом молекулярно-динамического моделирования исследована энергетика таких границ. Получены количественные оценки удельной энергии ГЗ в альфа-железе, хроме, ванадии и бинарном сплаве Fe-10ат.Cr для температуры 300 К.

В случае ванадия наши результаты качественно согласуются с соответствующими ре- зультатами, полученными ранее Псахье и др. [9] на основе того же потенциала межатомного взаимодействия, но для очень низкой температуры (10К). По абсолютной величине наши оценки оказываются на = 10% выше. Это отличие объясняется различными температурами моделируемых бикристаллов.

Моделирование двойниковых ГЗ в бикристаллах альфа-железа, ванадия, хрома и бинарного неупорядоченного сплава Fe-10ат.Cr показало, что значения их удельных энергий лежат в относительно узком интервале от 0,054 до 0,087 eV/ А 2 . Наибольшими удельными энергиями обладают межзеренные границы в ванадии, наименьшими – в альфа-железе и сплаве Fe-10ат.Cr.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг, ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы и при частичной поддержке гранта РФФИ – проект 12-08-97076