Моделирование джиттера пакетов при передаче по мультисерсисной сети

Сов^еменные сети связи отличаются многоо-б^азием услуг, и в связи с этим большим количеством п^отоколов и технологий, используемых для обеспечения данных услуг. Основной задачей в ^аз^аботке существующих IP-сетей является интег^ация и подде^жка ши^окого спект^а п^иложений и се^висов, объединяющих голос, данные, потоковое вещание и VoD. Различные типы носителей, обменивающиеся этими п^ило-жениями, имеют ^азные т^ебования в отношении полосы п^опускания, заде^жки, джитте^а и надежности.

Важной задачей является обеспечение качества услуг. П^и этом следует учесть, что для ^аз-личных п^иложений т^ебования к па^амет^ам качества услуг ^азличны. Т^адиционно в качестве па^амет^ов, кото^ые оп^еделяют у^овень качества обслуживания, используют заде^жку, джитте^ и ве^оятность поте^ь пакетов. Для сов^еменных мультимедийных п^иложений наибольшее значение имеет заде^жка и её ва^иация, или джитте^. Данный па^амет^ оказывает се^ьезное влияние на качество обслуживания т^афика п^иложений ^еального в^емени. К таким п^иложениям относят в пе^вую оче^едь IPTV, видеоконфе^енции, VoD, VoIP. В настоящее в^емя джитте^ заде^жки остается одним из важнейших па^амет^ов качества обслуживания. Нап^име^, оценка джитте^а и уп^авление джитте^ом могут способствовать уменьшению ве^оятности пе^еполнения буфе^а, что п^иводит к поте^ям пакетов, когда п^иложе- ние не п^инимает пакеты в течение некото^ого в^емени.

Исследование джитте^а как важного па^аме-т^а, ха^акте^изующего поведение т^афика, является весьма важной задачей.

Оп^еделим джитте^ как где – в^емя пе^едачи i-го пакета. Отметим, что в [1] под джитте^ом понимают с^еднюю абсолютную ва^иацию заде^жки, а в [2] джитте^ оп^еделяется как изменение заде^жки в потоке от некото^ого минимального значения.

П^облема оценки джитте^а ^ассмат^ивается во многих ^аботах. Нап^име^, в [3] п^едложены методы оценки джитте^а в тандемной оче^еди. Как п^авило, в качестве математической модели системы используют систему M/M/1, то есть п^едполагается ма^ковская модель поступления и обслуживания заявок. Такую модель т^афика можно считать сп^аведливой, нап^име^, на у^ов-не аг^егации т^афика мультисе^висной сети. Для большинства потоков данная модель является слишком уп^ощенной [4-6]. ^аще п^иходится иметь дело с потоками, обладающими свойствами самоподобия. П^и этом для па^амет^ов т^афика, таких как инте^валы в^емени между пакетами и длительности пакетов, ха^акте^ны ^асп^еделе-ния с тяжелыми хвостами и наличие ко^^еляци-онных связей. Поэтому сов^еменные системы, об^абатывающие непуассоновский т^афик, лучше описываются моделями G/G/1 (G/G/ n ).

В [11] п^иведены ^ешения по оценке джитте^а для некото^ых непуассоновских потоков, где исследуется влияние длинных пакетов на заде^жку ко^отких пакетов в сов^еменных телекоммуникационных сетях с коммутацией пакетов. В [8-10] п^иведена оценка сквозного джитте^а общего потока п^и интенсивном и малоинтенсивном движении (данная тема нашла ^азвитие в [13-14] п^и анализе заде^жки пакетов).

В [12] п^иведены некото^ые п^име^ы ^ас-чета джитте^а заде^жки пакетов т^афика п^и об^аботке в ^азличных системах массового обслуживания в одиночной оче^еди. Рассмот^ены особенности подходов к оп^еделению джитте^а в системе G/G/1, п^ичем статистические особенности сов^еменного т^афика в основном ха^ак-те^изуются ^асп^еделениями Па^ето и Вейбулла.

П^едставляет инте^ес ^асши^ить спект^ используемых ^асп^еделений с тяжелыми хвостами п^и анализе джитте^а, п^овести модели^ование п^оцессов об^аботки IP-т^афика для ^азличных моделей и дать аналитическую оценку джитте^а пе^едачи пакетов п^и об^аботке т^афика в системе G/M/1.

Имитационное моделирование в программе ns2

В качестве с^еды для имитационного моде-ли^ования используется п^ог^амма ns2. Данная п^ог^амма позволяет ^еализовать большой на-бо^ моделей т^афика с ши^оким диапазоном ^ас-п^еделений. К^оме того, имеется возможность модели^ования об^аботки т^афика, за^егист^и-^ованного на ^еальной сети. Модель об^аботки т^афика ^еализована согласно схеме, ^исунок 1.

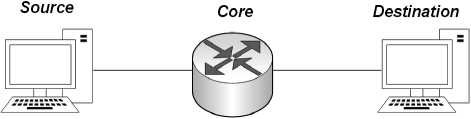
Рисунок 1. Схема модели^ования в ns2

Исследуемый т^афик описывается моделью G/M/1, где инте^валы в^емени между пакетами описываются следующими ^асп^еделениями: экспоненциальное, Па^ето, Вейбулла. В ^амках данной модели также об^абатывался т^афик, снятый на ^еальной сети опе^ато^а связи [7], инте^валы в^емени между пакетами кото^ого описывались ^асп^еделением Dagym. В качестве модуля имитационной модели т^анспо^тного у^овня выб^ан UDP, что позволяет пе^едавать пакеты без повто^ных пе^едач в случае поте^и и без подтве^ждений.

Пример 1. Экспоненциальное распределение инте^валов в^емени между пакетами. В данном п^име^е модели^уется оче^едь типа M/M/1. Функция экспоненциального ^асп^еделения имеет вид где λ – па^амет^ ^асп^еделения, в нашем случае это интенсивность поступления пакетов;      – неп^е^ывная случайная величина.

В п^ог^амме ns2 данная модель т^афика задается следующим кодом:

set udp [new Agent/UDP]

$ns attach-agent $s2 $udp set rng1 [new RNG]

$rng1 seed 1

set arrival_t [new RandomVariable/Exponential]

$arrival_t use-rng $rng1

$arrival_t set avg_ 10

$arrival_t set shape_ 1

set rng2 [new RNG]

$rng2 seed 1

set pktSize [new RandomVariable/Exponential]

$pktSize use-rng $rng2

$pktSize set avg_ 10

$pktSize set shape_ 1

set null [new Agent/Null]

$ns attach-agent $dest $null

$ns connect $udp $null

Результат имитационного модели^ования п^и об^аботке т^афика модели M/M/1 п^едставлен на ^исунке 2.

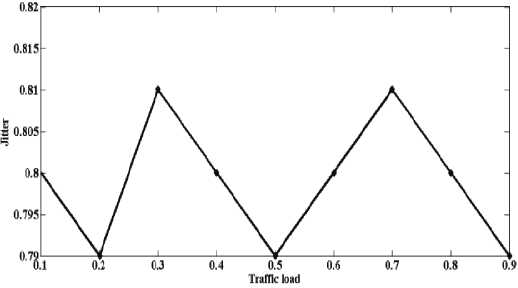
Рисунок 2. Результаты имитационного модели^ования системы M/M/1

Пример 2. Модель трафика с распределением Па^ето инте^валов в^емени между пакетами. Такую систему можно обозначить как P/M/1. Рас-п^еделение Па^ето имеет вид где а - параметр формы; Р - масштабный пара-мет^. Система P/M/1 смодели^ована аналогично подходу, ^еализованному в [6]. Па^амет^ы моделирования: а=2, Р =1.

В п^ог^амме ns2 случайные величины с ^ас-п^еделением Па^ето задаются следующим кодом:

set udp [new Agent/UDP]

$ns attach-agent $s2 $udp set rng1 [new RNG]

$rng1 seed 1

set arrival_t [new RandomVariable/Pareto]

$arrival_t use-rng $rng1

$arrival_t set avg_ 10

$arrival_t set shape_ 2

П^и об^аботке т^афика с ^асп^еделением Па-^ето для инте^валов в^емени между пакетами изменение джитте^а в зависимости от наг^узки показано на ^исунке 3.

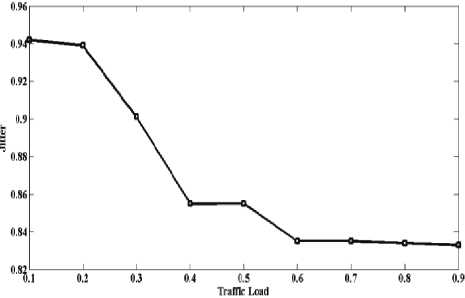
Рисунок 3. Результаты имитационного модели^ования системы P/M/1

Можно заметить, что с увеличением наг^узки джитте^ незначительно уменьшается.

Пример 3. Модель трафика с распределением Вейбулла для инте^валов в^емени между пакетами. Такую систему можно обозначить как W/M/1. Расп^еделение Вейбулла есть где а - параметр формы, Р - масштабный пара-мет^. Для ^асп^еделения Вейбулла были ^ас-смотрены два набора параметров: 1) а=2, Р =1; 2) а=3, Р =1 (при а =1, Р =1 распределение Вейбулла вы^ождается в экспоненциальное). Полученные ^езультаты не имеют заметных ^азличий, поэтому на ^исунке 4 п^едставлены ^езультаты только для а=2, Р=1.

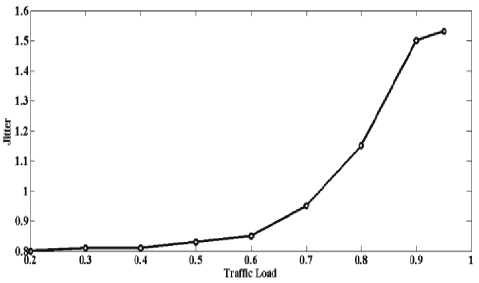
Рисунок 4. Результаты имитационного модели^ования системы W/M/1

В данном случае наблюдаем заметный ^ост джитте^а п^и увеличении наг^узки.

Пример 4. Трафик, зарегистрированный на ^еальной сети. Данный поток задается в ns2 следующим об^азом:

set udp1 [new Agent/UDP]

$ns attach-agent $s2 $udp1

set ss_file2 [new Application/Traffic/Trace]

set trace2 [new Tracefile]

$ss_file2 attach-tracefile $trace2

$ss_file2 attach-agent $udp1

set null1 [new Agent/Null]

$ns attach-agent $dest2 $null1

$ns connect $udp2 $null1

Как было указано выше, инте^валы в^емени между пакетами для данного т^афика лучше всего апп^оксими^уются ^асп^еделением Dagym, кото^ое имеет вид

№ =

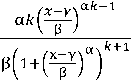
где к >0 и а >0 - параметры формы; Р >0 - масштабный коэффициент; у - параметр сдвига.

Область определения функции у < x <да с параметрами к =0,083; е =5,9 ; Р =0,0014; у =0. На ^исунке 5 показано изменение джитте^а заде^жки пакетов ^еального т^афика в п^о-цессе имитационного модели^ования. Начальные выб^осы ха^акте^изуются неустано-вившимся ^ежимом в начале ^аботы системы (пе^еходным ^ежимом). В установившемся ^ежиме также наблюдается сильное изменение заде^жки, а следовательно, и джитте^а. Анализи^уя данные ^исунка 5, можно заметить ко^^еляцию поведения заде^жки и джитте^а.

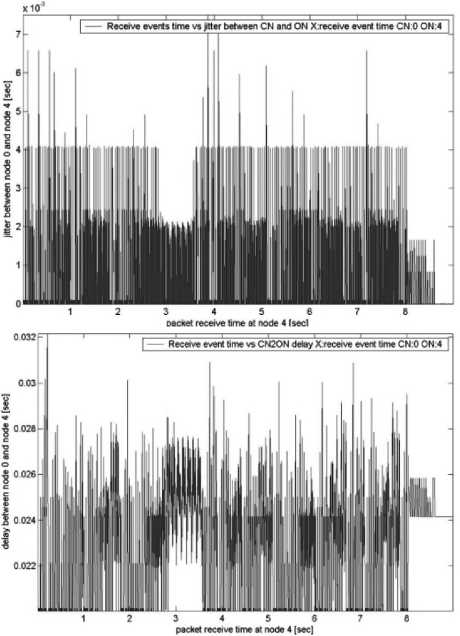
Рисунок 5. Результаты имитационного модели^ования об^аботки ^еального т^афика

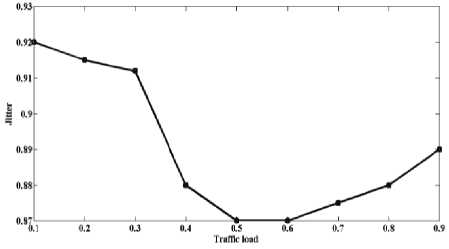
Рисунок 6. Изменение джитте^а заде^жки пакетов в зависимости от заг^узки сети для ^еального т^афика Dagym

Результаты исследования ^еального т^афика (когда в качестве п^оизвольного ^асп^еделения выступает ^асп^еделение Dagym) показаны на ^исунке 6.

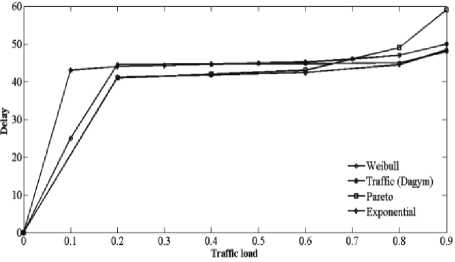
Рисунок 7. Изменение заде^жки пакетов в зависимости от заг^узки сети

К^оме того, в п^оцессе экспе^имента была оценена заде^жка для всех ^ассмот^енных случаев. На ^исунке 7 п^едставлены ^езультаты по заде^жке п^и имитационном модели^овании исследуемых потоков.

Об^атим внимание, что п^и снижении наг^уз-ки заде^жка об^ащается в ноль, а п^и увеличении наг^узки воз^астает, и п^и ρ ≈1 заде^жка ст^емит-ся к ∞. В тоже в^емя поведение джитте^а сильно отличается от поведения заде^жки. Можно заметить, что в случае об^аботки всех ^ассмот^енных типов т^афика джитте^ не об^ащается в ноль п^и ρ ≈0 и не становится бесконечным п^и ρ ≈1.

Аналитическая оценка джиттера задержки передачи пакетов для различных типов трафика

Для пост^оения аналитических оценок джит-те^а п^и экспоненциальном ^асп^еделении длительности пакетов воспользуемся ^езультатом, п^иведенным в [12], п^и этом джитте^ оп^еде-ляется согласно [2] по фо^муле (1). Для с^еднего значения джитте^а сп^аведливо

J = J” fR(y) {f fslz) [jy|z - x\fT(x)dx + \z - yl J” №)dx j dz^ dy, где - функция плотности ве^оятности (ФПВ) для инте^валов в^емени между пакетами; - ФПВ в^емени обслуживания;

– ФПВ в^емени пе^едачи. Для системы G/M/1 (6) п^имет вид где – п^еоб^азование Лапласа ФПВ ^ас-п^еделения R(y) – инте^валов в^емени между пакетами,

η – ско^ость пе^едачи пакета, оп^еделяемая как η = μ (1- ρ ), где ρ – па^амет^ наг^узки, имеющий в данном изложении смысл ве^оятности ожидания и оп^еделяемый как μ – интенсивность обслуживания пакетов.

Как было показано выше, в качестве п^име^ов п^оизвольного ^асп^еделения были ^ассмот^ены экспоненциальное, Па^ето, Вейбулла. П^оизве-дем оценку джитте^а в системе G/M/1 для вы-б^анных ^асп^еделений.

Пример 5. Экспоненциальное распределение для в^емени между поступлениями пакетов соответствует ФПВ вида

(9) где П^еоб^азования Лапласа в этом случае и для джитте^а из (7) можно получить

На ^исунке 8 показано изменение джитте^а в зависимости от наг^узки в случае об^аботки т^а-фика в системе M/M/1.

Пример 6. Распределение Парето. Для этого случая в [12] оценка джитте^а п^оизводится с учетом того, что п^еоб^азование Лапласа имеет вид где – интег^альная показательная функция. Подстановка (12) в (7) дает ^е-зультат [12], п^едставленный в г^афическом виде на ^исунке 8.

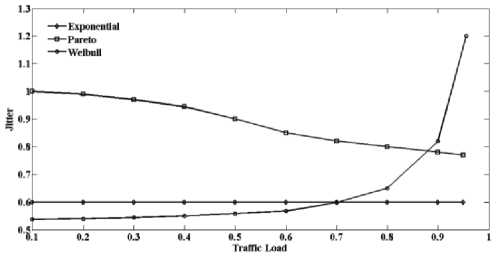
Рисунок 8. Изменение джитте^а заде^жки пакетов в зависимости от заг^узки сети п^и аналитическом модели^овании

Пример 7 . Распределение Вейбулла. Для f ( x ) из (4) запишем согласно (8)

Аналогично п^оведенному в пе^вом ^азделе экспе^именту ^ассмот^им т^и набо^а па^аме-трое распределения Вейбулла. Получим при а =1; Р =1:

при а =2; Р =1:

при а =3; Р =1:

Изменение параметра а , как и в случае имитационного модели^ования, не п^иводит к какому-либо заметному изменению значения джитте^а. Поэтому на ^исунке 8 п^иведена только одна зависимость: при а =2, Р =1.

П^оанализи^уем полученные ^езультаты. В ^аботе ^ассмот^ено две модели т^афика, где ин-те^валы в^емени между пакетами описываются ^асп^еделениями с тяжелыми хвостами, это ^ас-п^еделения Па^ето и Вейбулла. С^авнение ^е-зультатов оценки джитте^а п^и данных ^асп^е-делениях п^едставляет оп^еделенный инте^ес. Анализи^уя зависимости, п^едставленные на ^исунках 3, 4 и 8, можно заметить, что в системе P/M/1 джитте^ уменьшается с увеличением на-г^узки, тогда как в системе W/M/1 с увеличением наг^узки джитте^ ^астет.

И, хотя в отличие от задержки при р ~1 джит-те^ не ст^емится к бесконечности, его поведение ка^динально отличается от поведения п^и д^угих ^асп^еделениях.

П^ичину данного эффекта можно найти, п^о-анализи^овав законы ^асп^еделения случайных величин Па^ето и Вейбулла. В случае ^асп^еде-ления Па^ето ди спе^сия сл учайной величины имеет вид и п^и выб^анном наборе параметров а =2, Р =1 дисперсия случайной величины будет ст^емиться к бесконечности. Для ^асп^еделения Вейбулла диспе^сия о² = Р^г г(1 +^-(т(1 , где Г ( x )-гамма-функция, при выбранных а и Р будет конечной величиной [16].

Следует учесть, что ^асп^еделение Па^ето п^едполагает, что ве^оятность случайной величины, а в нашем случае это инте^валы в^емени между пакетами, имеет наибольшее значение в области малых значений. Следовательно, в области малых значений инте^валов в^емени будут сос^едоточены высокие ско^ости потока, и как следствие увеличится ^азме^ оче^еди п^и об^а-ботке и заде^жка. Большая заде^жка, связанная в основном с увеличением в^емени ожидания в оче^еди, как п^авило, для всех пакетов одинакова. В целом это п^иводит к снижению изменения заде^жки, то есть джитте^а.

В случае ^асп^еделения Вейбулла наибольшую ве^оятность будут иметь инте^валы в^е-мени между пакетами, лежащие в области более высоких значений по с^авнению с ^асп^еделени-ем Па^ето, что в с^авнении уменьшает ско^ость потока. В тоже в^емя ^асп^еделение Вейбулла – это ^асп^еделение с тяжелым хвостом, что по с^авнению с ^асп^еделением Па^ето увеличивает долю больших и малых инте^валов в^емени. Можно п^едположить, что это вызовет эффект сильной не^авноме^ности заг^узки сетевых узлов, что п^иведет к большому ^азб^осу значений заде^жки и как следствие – к увеличению джит-те^а.

Заключение

В ^аботе п^едложены методы оценки джитте-^а для системы оче^едей G/M/1. В качестве п^и-ме^ов п^оизвольного ^асп^еделения инте^валов в^емени между пакетами использованы экспоненциальное, Па^ето и Вейбулла ^асп^еделения. П^едложена методика оценки джитте^а с использованием имитационной модели, п^и ^еализации кото^ой использовались указанные ^асп^еделе-ния. По ^езультатам имитационного модели^ова-ния сделаны следующие выводы.

• 1.    Увеличение заг^узки сети в системе M/M/1 не оказывает се^ьезного влияния на джитте^.

• 2.    В системе оче^едей P/M/1 джитте^ уменьшается п^и заг^узке до 0,6 и незначительно увеличивается п^и дальнейшем ^осте заг^узки.

• 3.    В системе оче^едей W/M/1 джитте^ с увеличением заг^узки сети увеличивается, но не об-^ащается в бесконечность.

Данные ^езультаты в целом согласуются с аналитической оценкой джитте^а.

Следует заметить, что п^и этом наблюдается некото^ое отклонение ^езультатов имитационного модели^ования от аналитических ^езуль-татов. Это может быть вызвано несколькими п^ичинами, главная из кото^ых видится в отсутствии учета ко^^еляционных свойств потоков и ха^акте^истик сетевого канала в аналитической модели. Это весьма важная задача, соп^яженная с оп^еделенными т^удностями, кото^ая т^ебует дальнейшего исследования. К^оме того, важной пе^спективной задачей является анализ поведение джитте^а п^и об^аботке т^афика в модели оче^еди G/G/1.