Моделирование фазовой функции управляемых дифракционных элементов на основе линейного электрооптического эффекта

Элементы и устройства, основанные на электрооптическом эффекте, широко применяются для управления параметрами оптического излучения, например, интенсивностью, фазой, состоянием поляризации, спектральным составом [1]. Их достоинствами являются: высокое быстродействие (единицы ГГц), большая номенклатура функциональных материалов с различными физическими свойствами. В настоящее время на основе электрооптического эффекта разработаны объемные и планарные модуляторы, коммутаторы, дефлекторы широкополосного и лазерного излучения, перестраиваемые спектральные фильтры и т. п.

Одним из перспективных направлений развития данного класса устройств является разработка электрооптических управляемых дифракционных структур (УДС), обладающих перестраиваемой фазовой функцией [2]. В общем случае конструкция таких элементов включает электрооптический материал, управляющие электроды с индивидуальной или групповой адресацией, обеспечи- вающие требуемое распределение показателя преломления в объеме материала, а также комплекс функциональных покрытий, обладающих электроизоляционными, защитными, спектроформирующими или поляризационно-избирательными функциями (рис. 1).

Функциональное

Базовый элемент

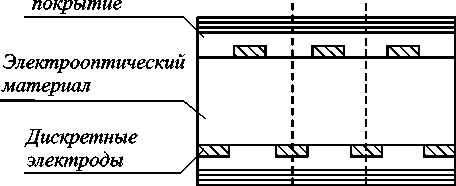
Направление световой волны

Рис. 1. Общий вид управляемой дифракционной структуры

Изменение вида фазовой функции с помощью одно-или многоканального источника напряжения приводит к формированию определенной диаграммы направленности такой структуры и изменению спектрального состава.

Целью настоящей работы являлось моделирование фазовой функции управляемых дифракционных структур.

Поскольку УДС на основе дифракционных решеток образуют периодические структуры, то для удобства была разработана система условных обозначений структур. Система обозначений управляемых дифракционных структур основана на конструктивных признаках базового элемента. Под базовым элементом понимается элементарная часть конструкции, многократное повторение которой образует УДС. Данная система учитывает количество и тип электродов (непрерывный, дискретный) на каждой поверхности элемента, распределение потенциалов по электродам, наличие функциональных покрытий. Условное обозначение базовых оптических элементов предлагается производить по следующей структурной формуле:

N ( X , - Y - Z , ): р

1(м, -R - K1):T, ’ где N, - количество повторений базовой структуры; X M, - число электродов верхнего (нижнего) слоя базовой структуры; Y, = {ND, R, = {ND - тип электродов верхнего (нижнего) слоя (N- непрерывный или D - дискретный); Z, = {01, K, = {0, указывают на распределение потенциала на верхних (нижних) электродах (0 - потенциал всех электродов одинаков, , - потенциал электродов различен); P, = {0,, T, = {0, - наличие (1) или отсутствие (1) функционального верхнего (нижнего) слоя базовой структуры.

Примеры основных типов базовых элементов с их обозначениями и описаниями приведены в табл. 1.

Поскольку структура электрического поля в дифракционных УДС достаточно сложна и тип преимуществен- ного типа электрооптического эффекта существенно зависит от соотношения геометрических размеров УДС и свойств электрооптического материала, то для оценки эффективности конструкции и используемого типа электрооптического эффекта сформулированы локальный и интегральный показатели эффективности элементов:

• -    показатель преимущественного типа электрооптического эффекта

  g ij

  
  

  xx к -и. -а. .

  i , j      , j ^i , j

  xx

  к. - • n. • a.

  i , j i , j        i , j

  
  

  _-

  
  

yy i, j ni, j ai, j

E , ⁿJ

• -    показатель электрооптической эффективности УДС

nm

G = EE g.j = i=1 j=1

nmnm

EEI EXГ «, X-EEI EX./«.-XA i =1 j =1                               i =1 j =1

nmnm

EEI EX , v4E2 E X.r-^г a y, I i =1 j =1                                   i =1 j "=1

где | E^x . _j |, | E yy | - абсолютные значения проекций вектора напряженности электрического поля на оси координат x , у ; i , j - дискретные координаты точек пространства, в которых рассчитывается функционал; « , m - количество точек в дискретном пространстве по осям x , у ; « , , a x.. , О' -показатель преломления электрооптического материала и проекции вектора направления распространения световой волны на оси координат x , у для точки i , j дискрет -ного пространства.

Эти показатели учитывают как конструктивное исполнение элемента, так и свойства выбранных электрооптических материалов и средств управления и позволяют провести оптимизацию параметров управляемого дифракционного элемента по определенному показателю или их группе.

Здесь показатель g характеризует эффективность электрооптического эффекта в выбранной точке про-

Примеры типовых структур базовых элементов УДС и их обозначения

Таблица 1

Условное обозначение Краткое описание Структура базового элемента 1 - N - 0 1 - N - 0 Последовательная структура с одним верхним и одним нижним непрерывными электродами без функциональных слоев 2 - D -1 1 - N - 0 Последовательная структура с двумя дискретными электродами с разными потенциалами верхнего слоя и одним непрерывным электродом нижнего слоя без функциональных слоев (2 - D-1):1 1 - N - 0 Последовательная структура с двумя дискретными электродами с разными потенциалами верхнего слоя и одним непрерывным электродом нижнего слоя, с одним верхним функциональным слоем 2(2 - D-1):1 1 - N - 0 Последовательно-параллельная структура, состоящая из двух базовых элементов, каждый из которых включает два дискретных электрода с разными потенциалами на верхнем слое и один непрерывный электрод на нижнем слое, а также один верхний функциональный слой Кх Wxxxx ух .х х х х? странства (локальный показатель), G - среднеинтегральную эффективность базового элемента (интегральный показатель).

Частным случаем формул (1), (2) является случай, когда направление распространения световой волны совпадает с одной из координатных осей x , у . Тогда выражения для показателей эффективности принимают вид:

g -,j

E-j

Exj

^^^^^^»

+ E yj

nm

G = EE g -j =

i =1 j =1

nmnm

EEI Ex, I-EEIEij|

= i = ,-' i = j _____            (4)

n m           n m

EEI E j + EEI e , i =1 j =1               i =1 j =1

Диапазон изменения значений локального и интегрального функционалов g j и G - от минус одного (-1) для продольного (вдоль координатной оси y ) электрооптического эффекта до плюс одного (+1) для поперечного электрооптического эффекта (вдоль координатной оси x ). Задавшись классификационным уровнем по выбранному показателю (например, 0,1) можно получить численную оценку эффективности моделируемого электрооптического дифракционного элемента.

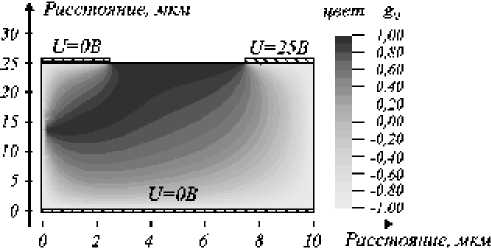
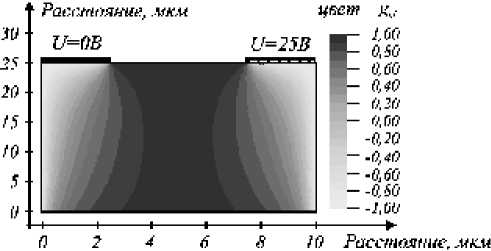
Примеры распределения локального показателя эффективности g для базовых элементов типа (2- D -1):1 и (2- B- 1):1/(1- N-D ) приведены на рис. 2,3.

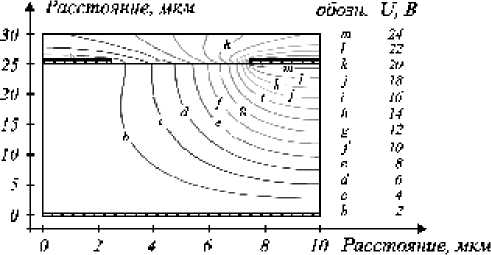
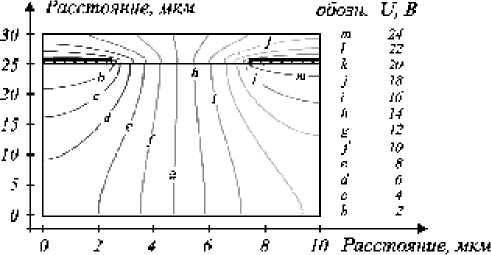
чески 100 % поперечный электрооптический эффект в центральной области и смешанный эффект в боковых областях (см. рис. 2), поэтому для рационального использования возможностей данного элемента следует выбирать тип и ориентацию электрооптического материала, обеспечивающие поперечный электрооптический эффект. Элемент типа (2- B- 1):1/(1- N-D ): обеспечивает смешанный электрооптический эффект в межэлектродной области, с преимущественно поперечным характером в верхней части и продольным - в нижней (рис. 3), поэтому для рационального использования возможностей данного элемента следует дополнительно исследовать электрооптическую эффективность для различных ориентаций кристаллов. Принципиальным отличием элемента данного типа от рассмотренного ранее является возможность создания наклонного линейного или нелинейного фазовых профилей, поскольку области преимущественно поперечного и продольного эффектов имеют приблизительно треугольное распределение.

б

Рис. 3. Пример распределения локального показателя эффективности g .j ( а ) и эквипотенциальные линии электрического поля ( б ) в базовом элементе типа (2- B- 1):1/(1- N-D ):

б

Рис. 2. Пример распределения локального показателя эффективности g . ( а ) и эквипотенциальные линии электрического поля ( б ) в базовом элементе типа (2- D -1):1

Элемент (2- D -1):1 с выбранными конструктивными и геометрическими параметрами обеспечивает практи

Для более точного математического моделирования процессов в УДС определена зависимость показателя преломления для световой волны с произвольным направлением и состоянием поляризации от типа и ориентации электрооптического кристалла, напряженности управляющего электрического поля. В результате разработана математическая модель, учитывающая изменение оптической индикатрисы электрооптического кристалла под действием составляющих электрического поля в произвольно ориентированном кристалле, и найдена конечная формула, связывающая значение показателя преломления n p ₂ с исходными данными задачи:

( ^k 2 z 2 ^Ь 2 - ^b3 k 2 y 2 ) 2

^{+ ( b} 3 ^k 2 x 2 - ^k 2 z 2 ^b 1^{)2 +}

h

2 П Г     / _ z x _ z         .

Дф ^{( x} ) =— J ^A n ( ^Ea ( ^x , y ) ; ^Ec ( ^x , y ) ) dy ,      (5)

^A 0 0

' — к b 1

'2 y 2   ^2 x2^U2 )

np2  V B + C + D + E + F + H + J ’

^B = ^b 1 ^b 3 ^k 2 x 2 ^k 2 y 2 ^d 3 - ^{2 b} 1 ^b 3 ^k 2 x 2 ^k 2 z 2 c 2 ^{+ b}1^k 22 x 2 c 2 ;

C = - b 2 Ь з k i² d 3 + b² c i k 2 y 2 + b 3 b 2 k 2 x 2 k 2 z 2 d 1 ;

D = - 2 bbkj^c, + ck 2 J x 2 - bbdk ;

232 y 22 z 2112 z 221322 y 2

^1^2^2 y 2^2 z2^2 ⁺ "1 ^л2 y 2 ^c 3   ^2 x 2ⁿ'2 y 2^3 ^W1 ;

где X 0 - длина волны используемого излучения, м; h -толщина электрооптического материала, м; A n - измене -ние показателя преломления под действием электростатического поля; E_a ( x , y ), E_c ( x , y ) – проекции напряженности управляющего поля на осях a и c кристалла соответственно, В/м.

В результате моделирования получено, что на основе структур типа (2– B –1):1/(1– N–D ): могут быть созданы УДС различного типа, например, рассеивающего, а также управляемые дифракционные решетки «с блеском»,

F = - 2 k 2 x 2 k 2 y 2 b i b 2 c 3 + k 2 x 2 k 2 y 2 b 2 Ь з d 2 - k 2 x 2 k 2 z 2 b 2 d 2 ;

H = k² b .² c - k.^^2d + k,„,k,,,bKd_A ;

2 x 2232 y 22 z 2132 y 22 z 2131

J = - bbk² „d , + k-^kMd + k 2 o b ² c, ,

122 z 212 x 22 z 21232 z 212

где k _{2 x 2}, k _{2 y 2}, k _{2 z 2} – направляющие косинусы световой волны в системе координат кристалла, а коэффициенты b ₁, b ₂, b ₃, c ₁, c ₂, c ₃, d ₁, d ₂, d ₃ вычисляются следующим образом:

b l = P 2 y 2 ⁺

p 2 z 2 ( ^k 2 y 2 p 2 x 2

2 x 2 p 2 y 2 ) ;

b3 = -

c ₁

c ₂

^k 2 x 2 p 2 z 2

^k 2 z 2 p 2 x 2

^b 2      p 2 x 2 ;

p 2 x 2 ^{( k} 2 y 2 p 2 x 2

^k 2 x 2 p 2 z 2

B

^k 2 x 2 p 2 y 2 ) ^;

^k 2 z 2 p 2 x 2

14" ⁺ r ll E x 2 ⁺ r 12 E y 2 ⁺ r 13 ^Ez 2 I

. n x 2                                      ) ;

Ц" ^{+ r}21 E x 2 ⁺ r 22 E y 2 ^{+ r} 23

I n y 2

;

c 3    I 2 ⁺ r 31 ^Ex 2 ⁺ r 32 ^Ey 2 ⁺ r 33 ^Ez 2 I ;

к n z 2                              )

d 1 = ² ( r 6i E x 2 + Г 62 E y 2 + r 63 E z 2 ) ;

• ^d 2 = ² ( r 51 ^Ex 2 ⁺ r 52 ^Ey 2 ⁺ r 53 ^Ez 2 ) ;

• ^d 3 = ^{2 (} r 41 ^Ex 2 ⁺ r 42 ^Ey 2 ⁺ r 43 ^Ez 2 ) ,

;

если вектор напряженности электростатического поля E _x ( x , y ) между любыми двумя соседними электродами будет направлен в одну сторону.

Фазовые функции (5) для базового элемента типа (2– B –1):1/(1– N–D ): на основе a -среза ниобата бария-стронция марки SBN:75, c -ось которого перпендикулярна одномерной решетке управляющих электродов, приведены на рис. 4, 5. Ширина электродов и размер дифракционной щели составил 5 мкм, толщина электродов – 0,5 мкм, направление распространения световой волны задавалось параллельным х -оси кристалла. Толщина защитного покрытия (двуокись кремния) составила 0,11 мкм.

Изменение толщины кристалла влияет на распределение управляющего электростатического поля и вид формируемой фазовой функции (рис. 4, 5). А изменение потенциалов электродов определяет только высоту профиля фазовой функции, изменяет дифракционную эффективность элемента и осуществляет перестройку УДС по длине волны излучения.

Вид фазовой функции (3) элемента (2– D– 1):1 со следующими параметрами: электрооптический материал – ниобат бария-стронция марки SBN:75, c -ось которого перпендикулярна одномерной решетке управляющих электродов, ширина электродов и размер дифракционной щели составляет 5 мкм, толщина электродов равна 0,5 мкм, направление распространения световой волны – параллельное a -оси кристалла, представлен на рис. 6. Толщина защитного покрытия (двуокись кремния) составила 0,11 мкм.

где n_{x 2}, n_{y 2}, n_{z 2} – показатели преломления кристалла при отсутствии управляющего поля; r_lk – электрооптические коэффициенты, м/В; E_{x 2}, E_{y 2}, E_{z 2} – проекции напряженности управляющего поля на оси кристалла, В/м; p _{2 x 2}, p _{2 y 2}, p _{2 z 2} – направляющие косинусы вектора поляризации.

Для расчета электростатического поля в анизотропной среде проанализированы различные возможные методы решения: метод зеркальных отображений, граничных потенциалов, конформных отображений, а также методы, основанные на конечно-разностной аппроксимации [3; 4]. В итоге предпочтение было отдано численным методам решения, как наиболее универсальным. Для расчета электростатического поля в УДС был применен программный продукт FlexPDE 5,0 с использованием адаптивной треугольной сетки. Возможности созданного собственного программного обеспечения позволили также вычислять фазовую функцию ц( x ) на выходе УДС (с учетом состояния поляризации p _{2 x 2}, p _{2 y 2}, p _{2 z 2} и электрооптических коэффициентов r_lk ):

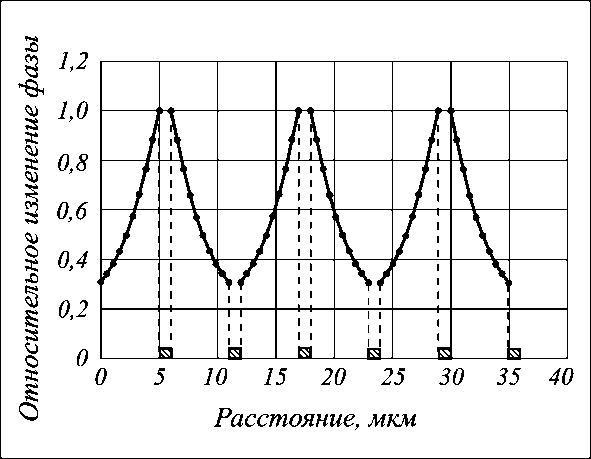
Рис. 4. Относительное распределение набега фазы по ширине дифракционной щели элемента (2– B– 1):1/(1– N–D ): с толщиной кристалла 11 мкм

Таким образом, видно, что формируемый вид фазовой функции – квазипрямоугольный со скважностью, определяемой шириной и периодом расположения электродов УДС; изменение потенциалов электродов определяет только высоту профиля фазовой функции (см. рис. 6).

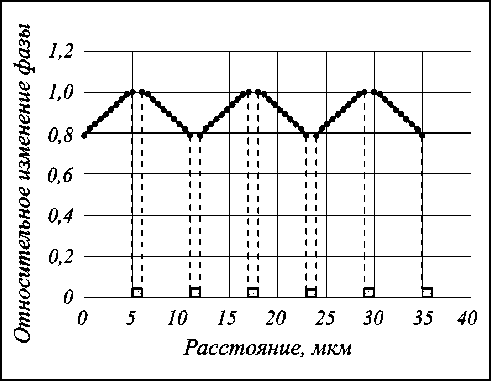
Рис. 5. Относительное распределение набега фазы по ширине дифракционной щели элемента (2– B– 1):1/(1– N–D ): с толщиной кристалла 100 мкм

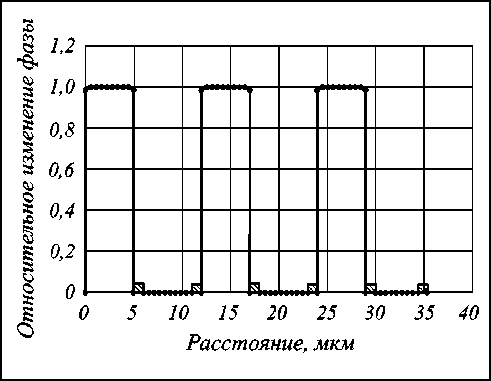
Рис. 6. Относительное распределение набега фазы по ширине дифракционной щели элемента (2– D– 1):1 с толщиной кристалла 100 мкм

Исследование элементов с различной толщиной кристалла показало, что для толщин SBN:75 порядка 2–3 периодов решетки электродов и более вид фазовой функции практически не изменяется, оставаясь приблизительно прямоугольным.

На основе структуры (2– B– 1):1/(1– N–D ): могут быть созданы элементы рассеивающего типа, а также управляемые дифракционные решетки «с блеском», наклонный фазовый профиль которых создается с помощью нескольких «ступенек» (см. рис. 5).

Таким образом, полученные модельные зависимости и расчеты позволяют анонсировать создание нового класса перестраиваемых дифракционных элементов, реализующих фазовые функции произвольного вида, например, квазипрямоугольные, линейные, квадратичные и т. д., что позволит реализовать элементы и устройства, выполняющие функции коммутации, модуляции, отклонения оптического излучения, а также изменение (коррекцию) его диаграммы направленности.