Проблемы нехватки и загрязнения водных ресурсов, их защиты от источников загрязнения для обеспечения населения чистой питьевой водой весьма актуальны в настоящее время. Эффективность мероприятий по защите подземных и очистке сточных вод подразумевает необходимость предварительной разработки эффективных методы и средств на основе комплексных исследований процесса фильтрации жидкости в многослойных пористых средах.

Несовершенство традиционных методов полива и вовлечение в сельское хозяйство подверженных к засолению земель приводит к тому, что ресурсы солоноватых возвратных вод в Узбекистане достигли значительных размеров. Поверхностные и подземные водоисточники продолжают загрязняться применяемыми в сельском хозяйстве минеральными удобрениями, ядохимикатами, пестицидами, сильноминерализованными и загрязненными коллекторнодренажными водами.

Организация прямого мониторинга процесса распространения токсических веществ в почвогрунтах не всегда целесообразна ввиду значительности трудовых и финансовых затрат. Поэтому более дешевой и эффективной альтернативой здесь выступают методы математического моделирования и вычислительного эксперимента. Математический инструмент позволяет выполнять как мониторинг, так и прогнозирование исследуемого процесса фильтрации, а также обеспечивать поддержку принятия управленческих решений, направленных на выделение изолированных областей, препятствующих проникновению различных ядохимикатов в зоны с относительно благоприятными экологическими условиями.

Математические модели процесса фильтрации подземных вод в многослойных пористых средах, обычно описываются системами дифференциальных уравнений в частных производных с соответствующими краевыми и внутренними условиями различного рода. Поэтому, к настоящему времени в области разработки математических моделей и вычислительных алгоритмов решения подобных задач уже получены значительные результаты прикладного и фундаментального характера.

В частности, значительный вклад в методологию математического моделирования фильтрационных потоков в многослойных средах оказали исследования М.С. Хантуша [1].

Авторами работы [2] произведен анализ запасов пресных вод с учётом изменения климата на основе разработанных математических моделей объекта исследования. Осуществимость и возможности этих моделей продемонстрированы на примере прогнозирования уровня грунтовых вод на пять дней вперед в засушливом и полузасушливом бассейне, расположенном на северо-западе Китая. Обнадеживающие результаты моделирования показывают, что методология может упростить и улучшить процедуру прогнозирования уровня подземных вод.

В.М. Булаватским с целью анализа и прогнозирования уровня подземных вод была разработана математическая модель для выполнения асимптотического анализа полей избыточного напора с фильтрационной консолидацией в двойной релаксационной системе [3]. Автором показано, что на начальных этапах консолидации учет релаксационных свойств деформируемой пористой среды важен в случае резких и значительных изменений в давлении. В общем случае, динамика фильтрационной консолидации пористой среды может быть численно смоделирована в рамках рассматриваемой математической модели.

• А. Власюком предложена математическая модель процесса переноса соли при фильтрации с учетом процесса инфильтрации в ненасыщенном слоистом грунте [4]. Для решения задачи был использован конечно-разностный метод и были проведены численные эксперименты на ЭВМ.

В рамках исследования [5] разработана математическая модель процесса фильтрации солоноватой воды с учетом температурного градиента для северных полузасушливых районов Китая. Результаты численного решения задачи показывают, что градиент температуры почвы оказывает определенное влияние на водно-солевую миграцию. Отмечено, что при проведении экспериментов влияние градиента температуры на миграцию соли было больше, чем влияние движения воды.

• Е.И. Андерсоном [6] рассмотрен двумерный устойчивый поток грунтовых вод в вертикальной плоскости и, получено аналитическое решение, используя которое проведено исследование взаимодействия воды с поверхностью грунтовых вод-потоков. Водоносный слой принимался идеализированным – в виде бесконечной полосы, а русло смоделировано в виде горизонтальной эквипотенциальной функции.

Общие методы решения задач двумерной фильтрации в анизотропных, неоднородных и многослойных средах рассмотрены в работе [7]. На их основе авторами предложены математические модели для изучения конкретных инженерно-технических проблем в водоснабжении, проектировании гидротехнических и гидромелиоративных сооружений. Исследование развивает теорию расчётов двумерных фильтрационных течений в многослойных неоднородных анизотропных средах для областей, ограниченных дугами координатных линий изотермических систем координат.

Д.С. Кузнецовым разработаны метод описания пространственной структуры потоков и математическая модель, позволяющая рассчитывать параметры структуры потоков подземных вод [8]. Задача геофильтрации здесь решается численно на основе разработанного автором алгоритма. Предложенный метод дает возможность решать задачи стационарного конвективного массопереноса в подземных водах в многослойной постановке и является основой для решения задач нестационарного массопереноса неконсервативного вещества.

В диссертационной работе Э.Р.Какушева [9] рассматривается связанная модель фильтрации в упругой пористой среде и дано обобщение на случай геометрически нелинейного деформирования. Как отмечает автор, эффект связанности появляется из-за взаимного влияния пространственной деформации каркаса грунта и изменения давления жидкости в порах.

Разработанная численная модель позволяет рассчитывать величины изменения порового давления, горизонтальные и вертикальные перемещения, в том числе проседания земной поверхности, а также напряжения и деформации. Также в работе реализована и несвязанная модель фильтрации в упругой пористой среде. Проведено сравнение моделей.

В статье [10] предложена методика реализации численной модели внутрикарьерных дрен. Выполнены прогнозные расчеты с целью эффективного осушения месторождения. Методом численного моделирования доказана эффективность применения лучевого дренажа и горизонтальных дренажных скважин для интенсификации осушения падунских отложений в прибортовом массиве карьера.

Достаточно хорошо изучены математические модели течений в открытых водотоках, основанные на уравнениях Сен-Венана для случаев при которых расходы в реках (каналах, дренах) или емкостях водоемов велики по сравнению с фильтрационным питанием или потерями.

Так, результаты серии экспериментов представлены в работе [11] при учете различных внутренних границ с постоянным напором. В проведенных исследования авторами наблюдались колебания уровня грунтовых вод и процесс проникновения морской воды в многослойные водоносные горизонты. Математическая модель была разработана для исследования проникновения морской воды в прибрежные водоносные горизонты под влиянием приливных колебаний и эксплуатации подземных вод. Гидрогеологические параметры в модели откалиброваны с помощью записей об уровне подземных вод и солености.

Авторами статьи [12] получены аналитические модели для прогнозирования загрязнения подземных вод в изотропных и однородных пористых средах. Влияние коэффициентов дисперсии и диффузии включается в решение уравнения адвекции и дисперсии и используются переходные (зависящие от времени) граничные условия. Аналитические решения получены с использованием метода интегрального преобразования Лапласа и концепции линейной изотермы. Численные решения получены явными конечно-разностными методами и сравниваются с аналитическими решениями. Численные результаты анализируются для различных типов геологических пористых образований, то есть водоносного горизонта.

В [13] представлена математическая модель динамики подземных вод при стационарном течении для изучения 2D-водоносного горизонта с пластом воды с постоянным наклоном, состоящим из однородных и изотропных сред. Разработан численный алгоритм для проведения вычислительных экспериментов по решению задачи как в однородной изотропной, так и в однородной анизотропной среде.

На основе предположения о плоском движении подземных вод в замкнутом водоносном горизонте исследователями в [14] были созданы математическая модель и численный алгоритм для исследования процесса фильтрационных потоков грунтовых вод в замкнутом водоносном горизонте с переменной h , которая была рассчитана методом конечных элементов. Численное исследование показывает, что результаты по методу конечных элементов находятся в хорошем согласии с вычисленными результатами по методу конечных разностей.

В статье [15] для прогнозирования изменения уровня грунтовых и напорных вод разработана математическая модель, учитывающая внешний источник, испарение, коэффициенты фильтрации, активную пористость, скорость фильтрации и двусторонние граничные условия. Для численного итерирования задачи разработан эффективный численный алгоритм, позволяющий прогнозировать изменения уровня грунтовых вод. Проведёнными численными расчетами установлено, что фильтрационная проницаемость, коэффициента потери воды и скорости фильтрации, связанные с уровнем воды, могут иметь серьезное влияние на экологический процесс.

Авторами исследования [16] разработаны две нелинейные математические модели в виде временных рядов для прогнозирования колебаний уровня грунтовых вод с использованием искусственных нейронных сетей. Эти модели были применены для прогнозирования колебаний уровня грунтовых вод в прибрежном водоносном горизонте. Одной из входных переменных являлся уровень прилива.

В статье [17] получено аналитическое решение, основанное на подходе функции Грина для решения обратной задачи. На основе требуемого уровня концентрации загрязняющих веществ и планируемого периода времени откачки, авторами определяется кратчайшее расстояние до берега реки, где присутствует максимальный процент речной воды. Модель разработана для замкнутого и однородного водоносного горизонта. Первоначально аналитические результаты, Ravshanov, N.; Abdullaev, Z.; Khafizov, O.

Modeling the filtration of groundwater in multilayer porous media;

полученные при разном времени откачки, скорости и различных значениях начальной концентрации, проверяются численно с помощью программного обеспечения MODFLOW.

Распределенная модель процесса фильтрация подземных вод в квазитрехмерной постановке и одномерная модель деформации пористой среды для многослойной системы водоносных горизонтов предложены в [18]. Как отмечают авторы статьи, разработанное математическое обеспечение позволяет адекватно смоделировать изменение уровня грунтовых вод вокруг насосной скважины, а затем рассчитать уплотнение слоев почвы. Полученные результаты исследования можно использовать для системы с многоскважинной и/или многослойной перекачкой.

В работе [19] рассмотрен процесс фильтрации нефти в пористой среде. Для определения коэффициента кольматации частиц вокруг скважины используются собранные данные лабораторных измерений по падению давления и концентрации стоков, который использовались для более точного прогнозирования.

Исследование [20] посвящено решению задач геофильтрации и геомиграции в многослойных системах, состоящих из нескольких водоносных горизонтов, разделенных слабопроницаемыми слоями. Математические модели разработаны при следующем предположении: в водоносном горизонте преобладают продольные потоки, а в отрывных слоях -перетоки. Массоперенос описывается уравнениями конвекции и диффузии. Для численного интегрирования поставленной задачи автором использовались неявные конечно-объемные разностные схемы. Также в работе приведены результаты численных расчетов по перераспределению потоков подземных вод и миграции загрязняющих веществ в системе двух водоносных горизонтов с действующими скважинами.

В работе [21] предлагается усовершенствованная математическая модель, которая описывает поток жидкости через связанную систему трещина-матрица с использованием подхода двойной пористости. Предлагаемая модель отличается тем, что уравнение потока в трещине содержит гиперболический член в дополнение к обычному дисперсионному члену, а уравнение матричного потока содержит член связи, который контролирует переходный характер обмена флюида из хранимой скальной породы в гидравлические проводники. Для описания ограниченных участков сорбции предлагается изотерма сорбции Ленгмюра, в то время как изотерма сорбции Фрейндлиха рекомендуется для описания неограниченных участков сорбции, доступных в матрице породы.

Стоит отметить, что авторами данной статьи также получены определенные результаты в области моделирования процесса массопереноса в многопластовых пористых средах. В частности, разработаны математическая модель и эффективный численный алгоритм для исследования процесса фильтрации и изменения солевого режима подземных вод с учетом внешних источников и испарения [22]. Разработанный математический аппарат позволяет существенно сократить объем натурных экспериментов по мониторингу и прогнозированию уровня подземных вод и концентрации солей и минимизировать дорогостоящие и ресурсоемкие экспериментальные работы.

Ряд работ [23, 24] был посвящен разработке математической модели для мониторинга и прогнозирования изменений уровня грунтовых вод и концентрации солей, а также для представления процессов затопления, засоления и заболачивания при проектировании гидротехнических сооружений. Разработанный численный алгоритм обеспечивает решение задачи прогнозирования изменений уровня грунтовых вод с учетом активной пористости, дебита в двухслойных пластах.

Вопросы комплексного исследования процесса влаго и солепереноса в почвогрунтах были рассмотрены в работе [25]. Численное моделирование осуществлялось с учетом кольматации пор грунта мелкодисперсными частицами; изменения коэффициента проницаемости почвы; водоотдачи и коэффициента фильтрации; изменения начальной пористости и пористости осевшей массы. Был разработан эффективный численный алгоритм, основанный на векторной схеме Самарского-Фрязинова со вторым порядком аппроксимации. При выводе математической модели принималось предположение о том, что градиент давления в канале постоянный и равен атмосферному давлению.

Анализ приведенных выше и других научных публикаций позволяет сделать вывод о том, что процессы фильтрации жидкости в многослойных пористых средах при учете различий физикомеханических свойств пластов и взаимосвязи между поверхностными и подземными водами изучены недостаточно. Например, в Узбекистане часто встречается такое строение почвогрунтов при котором под малопроницаемым покровным слоем, содержащим подземные воды со свободной поверхностью, находятся напорные хорошо проницаемые слои. И в целом, практика показывает, что необходимость решения задач водообмена регионального масштаба с сильным взаимодействием поверхностных и подземных вод, возникает достаточно часто при проектировании и эксплуатации гидромелиоративных объектов.

Это обусловливает необходимость рассмотрения проблемы массопереноса комплексно, с учетом всех взаимодействующих компонент, в чем и состоит цель настоящей работы.

• 2    Methods

Рассмотрим процесс неустановившейся фильтрации жидкости в хорошо проницаемом водоносном горизонте, сверху и снизу перекрытого слабопроницаемыми прослойками.

При неблагоприятной экологической ситуации в области (0 < x < l, 0 < у < т) для предотвращения распространения загрязнения возникает необходимость создать неподвижную изолированную поверхность на границе x = L > l .

Математическая модель исследуемого процесса фильтрации жидкости в многослойной пористой среде при учете основных законов гидродинамики описывается с помощью системы дифференциальных уравнений в частных производных с соответствующими внутренними и краевыми условиями:

1 а 5, = а2 5,'

a t a t

1 д 52   д252   к, д 5, ।           к3

д   = - 2 + т  Я   у=m2 + тз   т  Я   У=тз ’ I a 2 d t   д x2   T2 д у    2 3  Т2 д у д 5з  д 2 5з a 3 д t при

• 5, (x, у ’ 0) = 52 (x ’ 0) = 53 (x, у ,0) = 0,(2)

5,(x, т2 + т3,t) = 52(x, t),(3)

• 52< x, t) = 53( x, m 3’ t),

5,(x, m, t) = 0, ^l3-1 у=0 = 0, оу 1

52(0, t) = 5* = const, t>0, d521,-L= 0.(7)

d x ^lx = L

Здесь 51,52,53  - понижения напоров в трех слоях; a,, a 2, a 3  - коэффициенты трубопроводности; к,,к2,к3  - коэффициенты фильтрации; m,,m2,m3 - мощности слоев;

Ti = к^т^ (i = ,,3) - фильтрационные проводимости слоев. Индексы 1,2,3 - соответственно относятся к первому, второму и третьему слоям, y - вертикальная координата.

При этом условие (7) в данной модели должно обеспечиваться галереей скважин, расположенной при x = L , >  L , на которой необходимо поддерживать понижение или расход, приходящийся на единицу ее длины в виде определенной функции времени, подлежащей определению.

Для интегрирования поставленной задачи применим к системе (1) интегральное преобразование Лапласа, тогда имея в виду (2) получим p^=^

a i       5 y ²

p - _ d2 S 2 K           _K^ dS3 / a 2 S 2 dx2    T2 5 y (y=m2 + m3   T2 dy (y=m'

P — d² S з

— S 2 =--y a3      dy

Соответственно в этом случи система (8) будет подчинена следующим краевым условиям:

—

—

S 1 ( x , m ₂ + m ₃, p ) = S 2 ( x , p ),                                       (9)

S 2 ( x , p ) = S 3 ( x , m 3 , p ),

S i ( x , m , p ) = 0, ^dS 3|    -o

= ⁰ = ^{0 1}

—            V*

S 2 (0, p ) = —, ^p

^d-^ I x = L = 0. dx

Решение поставленной задачи можно получить в области изображения аналогичным способом [26]:

sh

—

—

S 1 ( x , y , p ) = S 2 ( x , p )

,

S 2 ( x , p ) =

p sh —mi

V ^a 1

S* ch [ ^ 2 ( p )( L ^{— x} ) ]

p

ch [ ^ 2 ( p ) L ]

—

—

ch p y

S 3 (x, p ) = S 2 (x, p)— ch

A ^a 3

I --------------------, p — m 3 a 3

где to2(.p) = p~ + k1 l—hh I ^m^i + k3 /—th • a2 T2 N a1 N a1 T2 V a3 V m 3-

Переходя к оригиналу вместо (15)-(17), получим

V _v V * ^{m —} y ch ^[ A ^{2 (} L ^{— x} ) ]

S1(x,y, t) = S m1     ch [ A 2 L ]

+

да

— Z Z ( — 1) ⁿ ( 2 n — 1 )

^П n = 1 j = 1

да

П     L— — x cos —(2 n — 1)----

»2 ( ^ (2) ) ^L

X

-exp^{[ —} ( j ) t ],

• ⁵ * ch [ A 2 ⁽ L ^— x ⁾]

^{5 2 (} x ’ t ⁾         ch [ A ₂ L ]

8 5 ”

+ —Z

^П n = 1

да

Z ( — 1) ⁿ

( 2 n — 1 ) cos ^П (2 n — 1) L x

⁵ з ( x , y , t ) =

^Ф 2 ( A ² n )

5 ch [ A 2 ( L — x )^| ^ch [ ^A 2 L ]

- exp' A ²) ) 1 ],

ОС да да

+ — Z Z ( — 1) ⁿ ( 2 n — 1 )

^П n = 1 j = 1

n      L — x cos —(2 n — 1)----

X

где

exp^{[ —} ( ^A

S ) 2 • ],

Ф 2 V ) ) = ( 2 n — 1 ) 2 + 4 ^{— 2} ^ 2

П n

^ф 2 ( ^A ) ;

A 2 = ^L;

m ₁ T ₂

Ф2 (A) = | + a2T2

T 1

a^n2 )m- a1

+

T 3

a₃ cos ^{2 )} m³

,

а ) j д — положительные корни уравнения

П 2_ (2 n — 1)² + -21L ctg L m = ^ l + 23L _tg A m i ,

4 L              a ₁ T ₂       a ₁    a ₂     a ₃ T ₂      a ₃

n = 1,2,...

Рассмотрим второй случай, когда с верху находится водоупор, а снизу действует постоянный напор, то есть

d 5 1|     _{= 0}

d y   y = ^m 0

5 з = 0 ,

Тогда в области изображения имеем:

ch

—

—

51 (x, y, p ) = 5 2 (x, p) — ch p m1

,

где

S 2 ( x , P ) =

S * ch [ to 3 ( p )( L - x ) ] p ch [ to 3 ( p ) L ]

S з ( x , y , p ) = S 2 ( x , p )

sh p y

^shJ—m 3 V a - 3

to 2(p ) = — + — pt-th P1Щ + — рё-cth РЙm₃ a 2    Т з N ^а 1   N a i      Т з N а 3     У ^а 3

Оригиналы (18)-(20) приведены ниже:

S ( x , y , t ) = S • с ЧаЫ ¹         '            eh [ A 3 L ]

”

+ 8^ Z Z ( - 1) ⁿ ( 2 n - 1 )

ⁿ n = 1 j = 1

/

n      L - x cos —(2 n -1)

® 3 ( 4 ³П )

X

y-ехр[-(^3n) t], с Л-S *eh [ A3 ( L - x )] S7 (x, 11 =

^2V '         eh [ A 3 L ]

8 S ”

+--Z n n =1

^

Z ( - 1) n

( 2 n - 1 ) cos ^П (2 n - 1) L^ x

^ф 3 ( « j³П )

- exPH jn ) ² t ^],

S 3 ( x , y , t ) = S

* y eh [ A₃ ( L - x ) ]

^m 3

ОС /    /

+ 8^ Z Z ( - 1) n ( 2 n - 1 )

ⁿ n = 1 j = 1

^eh [ A 3 ^L ]

cos ^П (2 n - 1)

L - x

L

^ф 3 ( 4 ³n )

X

^[-(j) t], где

Ф 3 (0 = ( 2 n - 1 ) ² + ⁴ L²^²

n ²

Ф 3 ( ^ ) ;

A 3 =       ;

^m 3 T 2

Ф 3 ( ^ ) =Г⁺ T a 2   T 2

T a1 cos2 4^ a1

+

T 3

a ₃sin ² i^

;

^j³ n - положительные корни уравнения

4 (2 n -1)2+р' ctg Цъ=+tg Lm1, n = 1,2,3,...

^{4 L}           a i T T 2     a а з    a 2   aT ^T 2    aa_i

Для определения понижений напоров при различных граничных условиях можно использовать следующие разложения мероморфных функций в виде суммы простейших дробей:

shaz _a  2n ® z , shbz b   b2 n=1

. a n n n sin----

.ⁿ + 1 b

/    A 2 ’

2 I n n 1

z ² + —

I b ^J

1 shaz      2 ” z _v

= a + - £ ( - 1 ) z chbz      b _n = 1

n - 1

chaz1

z= — + shbzb

£ ( - ! )•

ю

n = 1

an_z sin — ( 2 n -

2 b^V

² + ^ 2 (2 n

4 b2 V ann cos----

n

b

/ A 2 .

2 I П П ] z 2 + —

I b J

Для создания неподвижной изолированной поверхности перейдем теперь в области L <  x <  L 1 и функция S ₂( x , t ) должна удовлетворять двум условиям

S2(L + o,t) = S2(L -o,t), d S2 ।        d S2 , д    x=L+0         x=L-0

d x

Используем решение уравнения переменного S2 в области изображения. Тогда для первого случая будем иметь -         ~~

S2 (x, p) = c5 (p)sh[to1 (p)x] + c6 (p)ch[to1 (p)x].(21)

~~

Постоянные c ₅ ( p ) и c ₆ ( p ) определим из следующих условий для x g[ L , L 1 ]

dS2 (x=L+0 = 0.(22)

dx

S2( L1, p ) = Г1( p ),(23)

где Г 1 ( p ) - подлежит определению.

Так как литологическое строение пласта в области L <  x <  L 1 остаётся тем же, то & 1 ( p ) будет определяться формулой

(У 2(p) = p- + k1 Z-pcth /-pm1 + k3 /-pcth /-pm 1VP ’  a 2  T2^a,   ^a,  1  Т>^з ^3

Используя условия (22) и (23) из фо р мулы (21), найдём

S (x, p) = Г1(p)ch[y1(p Xx - LM(24)

2            ch[®!(p)(L. -L)]                                       ''

и приравнивая формулы *

S 2 ( x , p ) = S- ^{ch [ y 1(} p ^{)( L} " x ^)]

p    ch[ to 1 ( p ) L ]

с формулой (24) и получим

_F      S * chWp )( L - L )]

■

• ¹          pch ^[^⁽ p ) L ^]

Здесь предполагается, что выполняется неравенство L <  2 L . В частном случае при L = 2 L область становится симметричной относительно x = L , и понижение напора на управляемой галерее скважин станет равной S * .

Переходя к оригиналу в формуле (25), найдем по какому закону необходимо поддерживать понижение напора как функцию времени t на галерее, размещенной вдоль x = L 1 , чтобы поверхность, проходящая через точку x = L , была бы изолированной и неподвижной.

Из (25) находим оригинал

S' ch [ A ( L 1 - L )]

г i ( t ) ==--+

• ¹             ch ( A 1 L )

  Q С ОД ОД

  +— 2 2 ( - 1) n

  ⁿ n = 1 j = 1

  
  

( 2 n - 1 ) cos ^П (2 n - 1)———

-^х expH ^ j П ^{) 2} t ^]

Соответственно для случаев 1 и 2 в области изображений имеем

Г ₂( p ) =

Г з ( Р ) =

S * ch [ ^ 2 ( p )( L 1 - L )] p    ch[ ® 2 ( p ) L ]    ’

S * ch[ ® 3 ( p )( L 1 - L )] p     ^{ch [} ^ 2 ⁽ p ) L ^]    ’

где используются зависимости аналогичные (21) -(24).

Переходя к оригиналам в формулах (24) и (25), получим условия на управляемой галереи скважин для случаев 1 и 2 соответственно

8 S ”

+-- 2

^п n = 1

ОД

2 ( - 1) n

Г ₂( t) =

S*ch[A 2 ( L i - L )] ₊ ch ( A ₂ L )

(2n -1)cos [ П<2n - 1) L1 L L ] ф2 (3n)

х e^xp[ ^- ( j ) )² t ^] ,

8 S ”

⁺— 2

ⁿ n = 1

ОД

2 ( - 1) n

г      S * ch [ А з ( L - L )L

^{Г з ( t} ) =     ch ( A L )     ⁺

(2n -1)cos [I(2n- 1)L1 L L] фз(^3n)

^{х e}xpK ^- - ^{( 3} n ^{) 2} t ^] .

В том случае, если в качестве управления галереей скважин при x = L1 служит расход q(t), приходящийся на единицу её длины, то он будет определяться формулой д S2 I      _dS2 |      =_q(t)

д x l ^x = ^{1 1+ 0}    д x l ^x = L ^{1- 0}       T₂ .

Если x = L1 является плоскостью симметрии по отношению к x = L и x = L2 , то будет выполняться соотношение^S2= 0. Используя формулы (24) и (25), получим изображения д x \x= понижений напоров в основном водоносном горизонте в соответствующих областях

^S 2 ⁽ x, p ) =

• 5    * ch\ ^ 1 ( p )( x - L )] pchW'M P ) ^{L ]}

  (L <  x <  L) ,

  
  

S ,( x , p ) = ^s 'h '¹"'¹' ^{P )(} L ² - x ^)] (L <  x <  L₂ ) .

• ^{2    P}’     pch ^ V p ) L ]    ' ^{1        27}

Оригиналами этих выражений служат функции

( x , t ) = ^s ch A.x - L ^)] ₊

• ²             ch ( A 1 L )

  8 S ^{од +}— X

  
  

  n

  
  

  n = 1

  
  

  од

  X ( - 1) n

  
  

  ( 2 n - 1 ) cos ^П (2 n - 1) x—L

  .X^.    L

  
  

  — x ^exp^{[ - (} ^^ П ^{) 2} t ^)]

  
  

  8 S +

  
  

  од

  X

  
  

  ⁿ n = 1

  
  

  од

  X ( - 1) n

  
  

  ( L <  X <  L ),

  ( x , t ) = ^{Sch [} A , ( L 2 ^- x ^)]

  ²             ch ( A 1 L )

  ( 2 n - 1 ) cos

  [ П (2 n - 1) L 2^

  ^ф 1

  
  

  x ^exp^{[ -} ( ^ jП ) t ^]

  
  

⁽ L 1 <  x <  L 2 ).

На основании двух последних формул определяется приведенный расход q ( t ) на управляемой галереи скважин, или объединяя все случая, получим

Q i ( t ) = 2 ST 2 ^

4 од    од

^A i ^shA i ^{l +}yX X

^L n = 1 j = 1

( - 1) ⁿ (2 n - 1)²  .

--------/ x ----sin

^ф 1

П (2 n - 1) | exp[ - ( f jin ) ² 1 ] t ( i = 1,2,3) ,

где l = L ₂ - 1 1 = L 1 - L .

Из этого выражения видно, постоянные значения.

В выше указанных формулах

что при

константы

t ^од q i = 2 S T ₂ A i shA i l  ( i = 1,2,3) принимают

имеют следующие обозначения

A ² = A, ² + A ₃,   A ₂² = -k L,   a₃ ² = -k 3-

3                           3

m1T2        m3T2

.

• 3    Results and Discussion

0.25000 0.00000 0.20000 0.15000 0.10000 0.05000

На основе разработанного алгоритма проведены вычислительные эксперименты на ЭВМ по исследованию процесса неустановившейся безнапорной фильтрации потока жидкостей в многослойных неоднородных пористых средах, которые отличаются друг от друга гидрогеологическими характеристиками (рис.1-3).

1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21

8 сутка в верх вод. пласте     ^^^^w • 8 сутка в нижн. вод. пласте

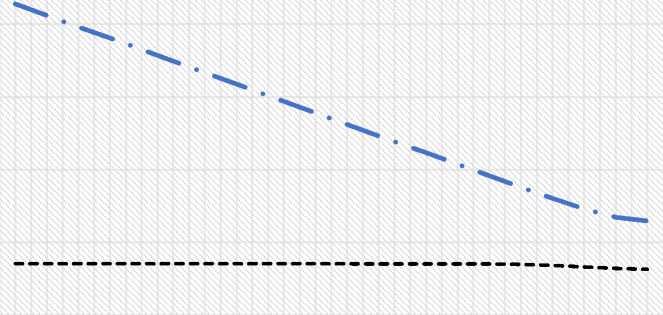
Рис.1 - Изменения напоров в пластах по длине фильтрационных слоев без учёта упругого режима Fig. 1 - Changes in pressure in layers along the length filtration layers without taking into account the elastic regime

0.18000

0.16000

0.14000

0.12000

0.10000

0.08000

0.06000

0.04000

0.02000

0.00000

1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17 18 19 20 21

• 4    сутка (в вех.вод. плас.)

0.12000 0.10000 0.08000 0.06000 0.04000 0.02000 0.00000

Рис. 2 - Изменение напора в верхнем фильтрационном слое без учёта упругого режима Fig. 2 - Changes in the pressure in the upper filtration layer without taking into account the elastic regime

Из кривых на рис. 1 видно, что понижение напора по длине верхнего фильтрационного слоя не наблюдается, тогда как существенное понижение напора по длине нижнего фильтрационного слоя (рис. 1, при t=8 сут.).

Ряд1         Ряд2

Рис. 3 - Изменения напоров со времени в верхнем и нижнем фильтрационных слоях без учёта упругого режима

Fig. 3 - Changes in heads with time in the upper and lower filtration layers without taking into account the elastic regime

Кривые на рис. 3 показывают, что со временем наблюдается повышение напоров в обоих фильтрационных слоях (верхнем и нижнем), происходящее по экспоненциальному закону.

Кроме того, анализ результатов проведенных вычислительных экспериментов при различных значениях гидродинамических параметров позволил выявить зависимость возникновения перетока жидкости через границу раздела фильтрационных слоев от значений проводимости и пьезопроводности хорошо проницаемых слоев, а также от значений коэффициентов фильтрации и пьезопроводности слабороницаемого слоя. Также по результатам вычислительных экспериментов установлена степень влияния упругого режима фильтрации в слабопроницаемом слое на перетеки в соседних пластах.

Разработанное математическое обеспечение, реализованное в виде программного средства позволяет строить схемы размещения и мощности скважин вертикального дренажа для защиты орошаемых и неорошаемых территорий от потопления и защиты подземных вод от источников загрязнения. Использование предлагаемого математического инструмента также позволяет получить прогнозные уровни грунтовых вод для любого рассматриваемого района за необходимый период времени с учетом различных факторов: неоднородность пласта в плане; уклон водоупора; инфильтрационное питание; испарение и др. гидрогеологических, гидротехнических и природных условий.

• 4    Conclusions

В заключении отметим следующее. Аналитическое решение поставленной задачи (1)-(7) в области изображения, то есть когда сверху расположен водоупор, а снизу действует постоянный напор, получено путем применения интегральноого преобразования Лапласа.

Получены решение задачи определения напора в слабопроницаемом фильтрационном слое и обобщенная формула для управления галереей скважина на основе приведенных расходов q i ( t ) .

Разработан метод получения аналитического решения математических моделей массопереноса в ограниченных областях с использованием теоремы Миттага-Леффлера о разложения мероморфных функций на простейшие дроби.

При различных граничных условиях получено соотношение для вычисления расходов галереи скважин для управления дебитами с целью создания неподвижной изолированной поверхности. Соотношение имеет вид суммы простейших дробей как разложения мероморфных функций. Также найдено условие для создания неподвижной изолированной поверхности для функции 52(x,t) . Способ создания водонепроницаемых поверхностей, при верхней границе, граничащей с атмосферой, определяется в виде функции, зависящей от координаты и времени.

Разработанное математическое обеспечение может быть использовано для предотвращения распространения токсических веществ путем выделения изолированных областей, препятствующих проникновению различных ядохимикатов в зоны с относительно благоприятными экологическими условиями.

• 5 Acknowledgements

  Работа выполнена в рамках проекта прикладных исследований (грант № БВ-Атех-2018-9), финансируемого Министерством инновационного развития Республики Узбекистан.