Моделирование фильтрационных течений в пласте при различных моделях фильтрации методом крупных частиц

При исследовании проблем естествознания в настоящее время активно и успешно используется численное моделирование. В современных задачах подземной гидромеханики сплошных сред необходимо решать систему нелинейных дифференциальных уравнений при заданных начальных и граничных условиях. Аналитические методы исследования позволяют решить достаточно узкий круг проблем, которые могут быть сформулированы в результате различных допущений и упрощений. Но вместе с этим простейшие задачи, допускающие аналитические решения, служат тестами при решении более сложных проблем.

В данной работе для решения задач фильтрации используется мощный метод современного численного эксперимента - метод крупных частиц [1-3 и др], хорошо себя зарекомендовавший при решении многих сложных задач механики сплошных сред.

Традиционным уравнением подземной гидромеханики, характеризующим процесс фильтрации жидкости, является линейный закон А. Дарси и его обобщение для «турбулентного» режима, когда пропорциональность скорости фильтрации градиенту давления заменяется квадратичной зависимостью и коэффициент проницаемости имеет размерность не площади, а длины [4,5]. Н Е. Жуковским [6] из общих уравнений гидродинамики при пренебрежении силами инерции аналитически выведен линейный закон А. Дарси. Фундаментальные работы в области нефтегазовой гидродинамики выполнены академиком СА. Христиановичем [7-10 и др.]. Как показала практика [7], совпадения данных опыта и численных расчетов, где в качестве динамического уравнения принимались линейный и двучленный законы А. Дарси, наблюдались только при медленных изменениях давления во времени. С.А. Христиановичем предложена новая модель фильтрации в условиях импульсного нагружения [7-9].

Следуя общей идее метода крупных частиц [1-3], дадим его описание применительно к системе уравнений изотермической фильтрации в пласте с переменной эффективной толщиной Цх, у) в случае, когда в качестве динамического уравнения принимается модельное уравнение С.А. Христиановича. Основная идея метода крупных частиц состоит в расщеплении исходной нестационарной системы уравнений движения подземной гидромеханики по физическим процессам.

Среда здесь моделируется системой крупных жидких частиц, совпадающих в данный момент времени с частицами эйлеровой сетки. Расчет каждого временного шага (вычислительного цикла) разбивается на три этапа: эйлеров, лагранжев и заключительный.

I - эйлеров этап, пренебрегаем всеми эффектами, связанными с перемещением элементарной ячейки (потока массы через границы крупной частицы нет), и исходная система уравнений сводится к динамическому уравнению. Здесь в расчетной области определяется поле гидродинамической скорости жидкости;

• II    - лагранжев этап, на котором при движении жидкости вычисляются потоки массы через границы эйлеровых ячеек (крупных частиц);

• III    - заключительный этап, когда на фиксированной исходной расчетной сетке определяются в новый момент времени значения параметров фильтрационного потока (плотности, давления, пористости) на основе закона сохранения массы для каждой ячейки и всей системы в целом.

Приведем алгоритм метода крупных частиц для моделирования фильтрационного течения однородной жидкости в пласте при использовании модельного уравнения С А Христиановича в качестве уравнения движения. Система уравнений изотермического движения в пласте с эффективной толщиной h(x, у) состоит из уравнения неразрывности - закона сохранения массы, уравнения С.А. Христиановича и баротропных уравнений состояния для жидкости и пористой среды:

, дот , ,    _„ h---+ drv(pmUh) = О, dt

^²(^ + Р-pVW)--y-U = 0,

Р=Р<ЛЛ, т~т(р).

где U = (m,v) - вектор гидродинамической скорости жидкости, р - плотность, р - пластовое давление, т - пористость, h - эффективная толщина пласта, р - безразмерная постоянная, зависящая от физических параметров пористой среды; величины [£'“]=1 и [2]=£² в уравнении С. А. Христиановича связаны с коэффициентом проницаемости к в модели А. Дарси следующим образом: к = Л ■ е² .

• I.    Эйлеров этап.

На этом этапе для каждой расчетной ячейки (др), как об этом уже говорилось, пренебрегаем всеми эффектами, связанными с ее перемещениями (отсутствует поток массы через границы ячейки). Поэтому убирается конвективный член из уравнения неразрывности, а жидкость предполагается заторможенной. Исходная система уравнений сводится, таким образом, к единственному соотношению - уравнению

С. А. Христиановича. Тогда du р йп.  ит

----) + —---и = т Sx 2

Р — dt dv          а Р       Р т л р — + е (— + Р----) + —--v = 0

dt ду т ду X ’ где производные по времени являются полными производными.

Аппроксимируя (2) в момент времени Г, получим следующие разностные уравнения в декартовой системе координат х, у для крупной частицы (/,/) :

р ,         Лк т         Лк         X м        4 м Ах u Ду р”.        Ду        т J Ay        X где величины с дробными индексами относятся к границам ячейки и равны полусуммам значений в смежных ячейках; например, для горизонтальной составляющей скорости

Таким образом, на первом этапе, в предположении заторможенности жидкости, по известному на слое /” распределению гидродинамических величин вычисляются значения скоростей м, v для центров крупных частиц.

• II.    Лагранжев этап

На данном этапе вычисляются эффекты переноса, учитывающие обмен между ячейками при их перестройке на прежнюю эйлерову сетку. Здесь находятся потоки массы ДА/" через границы эйлеровых ячеек за время Д/ При этом предполагается [13 и др.], что вся масса жидкости переносится только за счет нормальной к границе ячейки составляющей скорости.

Уравнение неразрывности системы (1) в разностной форме можно записать следующим образом (в предположении, что поток жидкости через ячейку (z',y) направлен слева направо и снизу вверх):

рХ, + ЬМ^_2; - ЬМ^,, + АЛ/”_;__1/2 - ДЛ/,"_Л1/2, где формулы для нахождения потока масс ХМ" имеют здесь следующий вид (например, для правой границы (z +1 /2, у) ячейки (z,y)) :

^^1+1/2,; ^< A+V2,/ ^> " <  ^Ui+V2,j > ' ^<  " ^< Ач-1/2,/ ^> "^У '

и т.д. Знак < > обозначает значения физических величин на границе ячейки. Выбор этих величин имеет важное значение, так как сильно влияет на устойчивость и точность вычислений [1,2]. Рассмотрим два вида аппроксимаций:

• а)    Можно определять \М” по формулам второго порядка точности, учитывающим направление потока. Рассмотрим, например, правую границу (z + 1 / 2, у) ячейки 0, у):

  
  
  
  

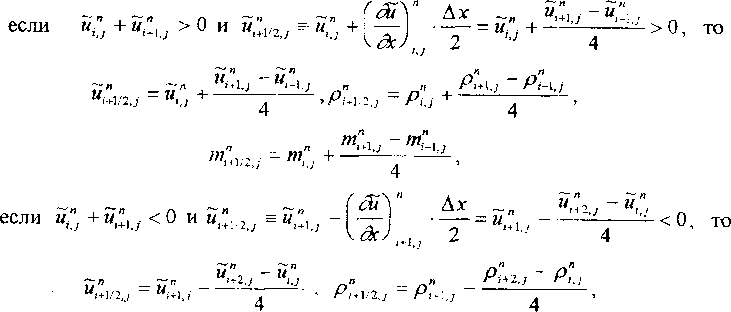
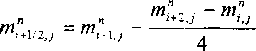
В противном случае, т.е.

~п —и    л ~п                1 ДХ ~п       i      i при м,,+   , > О и ы,= и + —--= и + -—------ < 0 или при и^ + и^ j < О и и^ = и\} -1 — |   • — = и^,—- > О, полагаем АЦ")/2? = 0.

• б)    Формулы первого порядка точности для потока масс -АМ”, также учитывающие направление потока, имеют следующий вид :

если и." + й"х> 0, то если иА + и^., <0, то

Кроме перечисленных двух типов аппроксимаций возможны другие способы вычисления величин   «("язц./рГи/г.г тм/2,р   вытекающие из особенностей рассматриваемого течения.

Значения на границе для эффективной толщины пласта можно вычислять по

А. + А,., .

формулам первого порядка точности h_M2J = —---- — или по формулам второго

,        ^u\,j + 2А ⁺ А-!,,

Здесь также возможны различные

порядка точности =--------------- подходы.

• III.    Заключительный этап

На данном этапе происходит перераспределение массы жидкости по эйлеровым ячейкам и определяются поля давления и плотности в новый момент времени. Из разностного аналога уравнения неразрывности (1.1) выразим значение плотности для нового временного слоя t'"^Y:

, AM"-AM"+ AM" -AM"

Ах■ Ay ^m-ty".

Баротропное уравнение состояния р = р^р^ позволяет вычислить новое значение давления в ячейке (/, у), где р = р(р) - функция, обратная к р= р(р}. В конце заключительного этапа вычислений полагаем и^ = й^, v^ = v,y

Вычислительный цикл, таким образом, закончен. В дальнейшем вся процедура повторяется сначала для следующего момента времени, т.е. для /”+2 и т.д. Можно показать консервативность разностных схем метода крупных частиц (выполнение закона сохранения массы для области интегрирования) и др.

Рассмотрим постановку начальных и граничных условий.'

• а)    На внешней границе области интегрирования может быть поставлено условие непроницаемости:

Считаем u_NVU2j = ---------. Без ограничения общности можно положить, что

PiVvij ~ Рн,р Рм*х; ~ Pnj^n+x,j ~*N.j>^mM,j "m^jA® Лч+ij ~ JNji

UN4.j ~ UN,pVNn,j - VHJ>PHrtJ ~ Ря.р

Для разностных схем второго порядка точности необходимо задавать два слоя фиктивных ячеек [1-3]. Используя центральные разности по пространственным переменным, для второго слоя ячеек можно записать следующее:

~ ^VM-lj>^WN+2J ~ ^тК-\,рРн*Х,1 ~ Pn-XJ '

• б)    Рассмотрим теперь условие свободного протекания на внешней области

интегрирования:

Полагая на первом слое фиктивных ячеек

“N+lj ~ UN.p VN,\j "" VN,j ’ Pn+\,j ~ Рч.р получаем для второго слоя фиктивных ячеек следующее:

^MN-2,7 ⁼ 2 • U_N j - U_N__X J , Vy_|2j ~  • V_Nj — V_{№ ]} J

= 2 ■ m”., - m;.^ , ^₊₂._; = 2 ■ p^ - ^ ,,.

• в)    Рассмотрим граничные условия, связанные с заданием расхода жидкости на границе области интегрирования.

Пусть, например, для ячейки (NJ) задан объемный расход (/) жидкости, вытекающей через ее правую сторону. Тогда разностную формулировку этого условия можно представить в следующем виде: Ay- Ь-т-и^_г} = q^ или, обозначая Ф - Ч^! (АУ И ту получаем й^п, = фУ)-

Полагая для фиктивных ячеек

Pn +1,7 ⁼ Рм.р Pn^.j ~ Pn,P^N+X,j ~ ^Nji^N+X.j ~^mN,p

UN^J = -«Lx,, - V”+2.y = VP) , j        ; , получаем значения давления во втором слое фиктивных ячеек:

„       „     4- Дх р V , _х

Постановка граничного условия заданного объемного дебита на стенке скважины формулируется точно так же, как и в случае задания объемного расхода на границе области. Полученные соотношения для фиктивных слоев ячеек позволяют единообразно проводить вычисления на границе области интегрирования:.

В качестве модельной рассматривалась следующая пространственноодномерная задача, допускающая аналитическое решение в двух различных постановках [5].

Случай 1. В полубесконечном пласте постоянной толщины h-const и ширины В начальное пластовое давление всюду постоянно и равно р_к. На галерее (при х = 0) давление снижено до p_g и в дальнейшем поддерживается постоянным. Давление в любой точке х и в любой момент времени t находится решением уравнения пиезопроводности [5] и выглядит так:

Р^0 = Р8 + (.Р, -Pg>         , где у - коэффициент пьезопроводности пласта.

При проведении численных экспериментов методом крупных частиц по обеим моделям условие на бесконечности р(х, t) = р_к при х —> оо заменялось условием открытой границы:

им = и" (п0 модели А. Дарси), мД, = “l (по модели С. А. Христиановича).                      (3)

Если применить схему второго порядка точности для модели А. Дарси, кь Pin - P1-Y = кЬП Pla г "Pc

p(pl) 2-Ах p(pLy) 2 k*

При использовании условия открытой границы (3.2) в модели С.А. Христиановича иьп иьп A/[z/L+1( Д.,.,]        {(£ )£+1 • [( ) -г р (~ду)Д,1 + иХп1 ~ ex pL+1           ас т ас л de pL        do т de л

Отсюда, полагая               Pln-Pi-> (а-²Д₄₁ = (е^Д,

P_LA - p_L, получаем следующий способ задания фильтрационных величин в фиктивных ячейках:

Pin = Pl » pLi^ ^Pl ~ Pin (модель А. Дарси),

Pin - Pl > Pin = Pl, Р1.г = Ж - pLy , ^ln = ^, ^ 2 = M - ™L > u^ = и”, и”^2 = 2м" - м” , (модель C.A. Христиановича) .

При проведении численных экспериментов характерные параметры по обеим моделям были следующими:

р_Й = Ю³ кг/ м³, р₀ = 10 МПа, р₍ = 10 ’ Па*с, L_o = 10 м, (б'Дц = 10~⁸,

Л„ =10"’ м², к₀ =10-" м², /₀ =10³ с.

Точность численных решений исследовалась в следующем диапазоне исходных данных :

°Р-Ро ^Рс ^{5 5}>⁰⁰ А/ °>⁵⁵’ Рк ^P_g ⁵ Ф⁰⁰' Рк\ 0,01-Д, <к<к₀;

0,010-(е²)_с<е² <1,00 (е²)_с-,0,20 /_о<25О-Г_о.                         (4)

В этом диапазоне проводилось сравнение численных и аналитических решений.

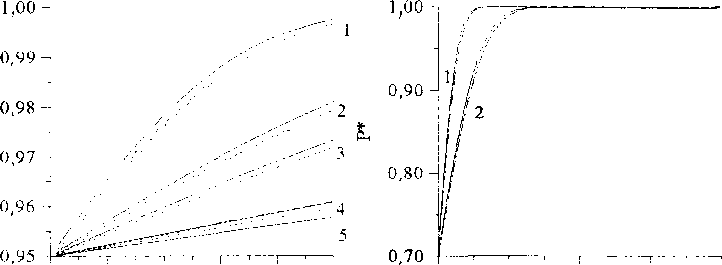
На рис. 1-8 по горизонтальной оси отложены X* - безразмерные расстояния до галереи, а по вертикальной оси отложены Р* = р / р₀ - значения безразмерного пластового давления. На рис. 1-8 представлены графики поля давления численных решений для модели С.А. Христиановича (штриховые линии), модели А. Дарси (штрихпунктирные линии) и аналитического решения (сплошные линии) в последовательные моменты времени (штрихпунктирные линии на рис. 1-8 полностью совпадают со штриховыми линиями).

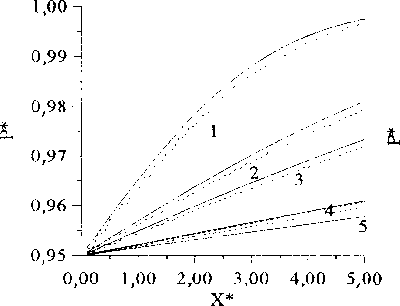
Рис. 1. Профили безразмерного давления в моменты времени:

/t = 1,0; /2 = 5,0; /3 = 10,0; /4 = 50,0; /5 = 100,0 при рк = 1; р8 = 0,95; р = 0,60; е2 = 1,0;

X = 0,10; к = 0,1; т = 0,30; ц = 1,00,

А = l,0;S = l,0;P/d =0,1;

=0,001

1,00 =

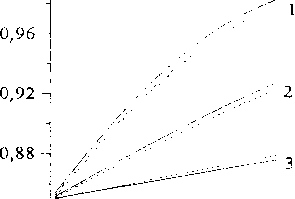
0,84 -----------। - - ,—;----,--,----,—г----------,

0,00 1,00 2,00 3,00 4.00 5,00

X*

Рис. 2. Графики безразмерного давления в моменты времени: /, = 1,0;/2 = 5,0;/3 = 50,0 при

Pt -^Р< = 0,85; Р = 0,20; g² = 1,0;

X = 0,10; к = 0,1; т = 0,30; ц = 1,00;

А = 1,0;5 = 1,0;р7Я =0,1,р^ =0,001

Предложенная численная модель интегрирования уравнения С А Христиановича и вычисления по модели А. Дарси показали высокую точность расчетов методом крупных частиц при сравнении с аналитическими решениями. Так, при всех вариантах исходных данных из (4) относительные ошибки численных решений по обеим моделям не превышали 1,5 %. При малых моментах времени, например при / = 0,20, наблюдается значительное отклонение численного решения по модели С. А Христиановича от точного решения, которое объясняется наличием больших градиентов давления в ячейках, расположенных вблизи галереи. При больших временных интервалах, например, при/ = 10,0, численное решение по модели С.А. Христиановича практически совпадает с решением по модели А. Дарси. Это также вполне физично и объясняется относительно незначительными изменениями пористости.

0,00 1,00 2,00 3,00 4,00 5,00       0,00   10,00 20,00 30.00 40,00

X*                               X*

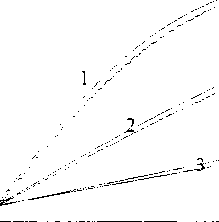
Рис. 3. Профили безразмерного давления в моменты времени:

1, = 1,0,7, = 5,0;/3 = 10,0,74 = 50,0,75 = 100,0 при рк = I, pg = 0,95; к = 0,1; е2 = 0,5;

л, = 0,20; т = 0,30; ц = 1,0; h = 1,0;

^1,0;Рх =0,1; Р^.= 0,001

Рис. 4 Графики безразмерного давления в моменты времени: к =10,0;/₂ =50,0 при

Рк = V P_g = 0,70; р = 0,60; е ² = 0,80;

X = 0,0125; к = 0,01; m = 0,25; ц = 3,70;

h = 1,0; В = 1,0; Р_х = 0,05, р_1гб4 = 0,001

1,00 !

0,00 1,00 2,00 3,00 4,00 5,00 X*

Рис. 5. Графики безразмерного давления в моменты времени: t_x = 1,0,7₂ = 5,0,7₃ = 50,0

при р. = 1, pg = 0,85; к = 0,1; е 2 = 0,50; X = 0,20; т = 0,30;

Ц = 1,0; h = 1,0; В = 1,0; р_;, = 0,1; p_sre, = 0,001

Случай 2. В таком же полубесконечном пласте, что и в случае 1, в момент времени 1 = 0 пущена в эксплуатацию галерея с постоянным дебитом 2о Требуется определить значение давления на расстоянии х от галереи в любой момент времени 1. Данная задача имеет аналитическое решение [5]:

Р(х,0 = Р8 +       *^/(-7=))+ С1 ехР( 7Г.Ж к        2^              4yt где Pg^-Pt--~----==-, Wj - скорость фильтрации на галерее. Характерные

В h к -Jtc параметры задачи были выбраны следующими:

р0 = 103 кг/м3, р0 = 10 МПа, L, = 10 м, (^2)0 = 10"s, Ло = 10'3 м2, kQ =10 11 м2, /0 = 103 с, 0о =1м3/с

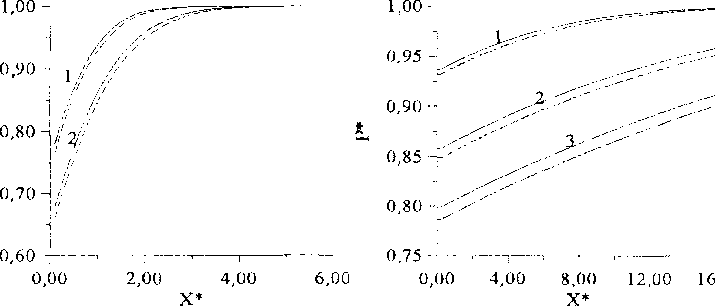
Рис 6. Профили безразмерного давления в моменты времени: /, = 5,0; /2 = 10,0 при рк = 1; Q, = 0,05; р = 0,15, е2 = 0,20;

X = 0,05; к = 0,01; т = 0,27; ц = 5,57;

А = 10,0; 5 = 10,0, Pjd =0,05;

Р^ = 0,001

Рис. 7. Профили безразмерного давления в моменты времени: t_x = 10,0;/₂ = 50,0;/, =100,0 при

Pt = 1; 0о = 0,05; р = 0,35, е² = 0,60;

Х = 0,5,к = 0,3;/и = 0,27;

ц = 5,57; 5 = 10,0,5 =10,0;

0„ = 0,05; p„d = 0,001

1,00

0,95

0,90

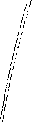
0,85

0,80

0,75 4-------'----:---------------------1 - п

0,00      2,00      4,00      6,00

X*

Рис. 8. Распределение безразмерного давления в момент времени: / = 5,0 при рк = 1; р = 0,15; 0О = 0,05; е2 = 0,20; 4 = 0,05, А = 0,01;/и = 0,27;

ц = 5,57,Л= 10,0; S = 10,0; p;d =0,05;рж^ =0001

Численные расчеты, проведенные при использовании обоих модельных уравнений движения в случае, когда на галерее задавалось условие заданного объемного дебита, показали, что относительная ошибка численных решений не превышает 3%.