Моделирование финансовых параметров компании на основе бухгалтерской информации и с учетом рыночной динамики

Автор: Мясин Антон Владимирович

Журнал: Имущественные отношения в Российской Федерации @iovrf

Рубрика: Управление собственностью - практический опыт

Статья в выпуске: 5 (116), 2011 года.

Бесплатный доступ

В статье представлен комплексный инструмент финансового анализа - модель ФинМод, при раз- работке которой автором сделана попытка учесть все необходимые составляющие планирования деятельности компании: устойчивый темп роста, моделирование финансовых сценариев в рамках системы уравнений Уоррена - Шелтона, рыночная динамика. Модель может быть использована при принятии управленческих решений, разработке бизнес-планов, для оценки стоимости предприятия с использованием доходного подхода. Доказаны ее практическая применимость и преимущество перед каноническими подходами.

Управление компанией, финансовое моделирование, устойчивый рост, рыночная динамика, планирование

Короткий адрес: https://sciup.org/170152178

IDR: 170152178

Текст научной статьи Моделирование финансовых параметров компании на основе бухгалтерской информации и с учетом рыночной динамики

1. Моделирование финансовых показателей

Прогнозирование – это один из обязательных инструментов успешного управленца. Когда компания достигает определенной «зрелости», возникает необходимость в моделировании сценариев дальнейшего развития бизнеса. На этом этапе создание стратегии развития становится важным элементом эффективного управления. В помощь менеджерам разработано множество инструментов, призванных помогать в управленческих решениях и давать развернутый ответ на вопрос: «А что будет, если?..». Проигрывая различные варианты или находя оптимальные сценарии, финансовое бизнес-планирование стало неотъемлемой составляющей управления.

Как уже было сказано, подобного рода инструментов создано множество. Важной особенностью каждого из них являются условия применимости и допущения, сделанные при его построении. А это значит, что сегодня не существует универсального средства планирования. Этот факт обусловливает разумность и необходимость создания новых финансовых моделей, позволяющих в конкретных условиях быть эффективнее существующих аналогов. Именно о такого рода инструментах мы и будем говорить далее.

В рамках настоящей статьи будет рассмотрено следующее: устойчивый темп роста компании и формула Хиггинса, моделирование финансовых сценариев в рамках системы уравнений Уоррена – Шелтона, необходимость учета рыночной динамики при планировании. Также будет представлена финансовая модель, при разработке которой мы попытались учесть все изложенное.

2. Скорость роста объема продаж, формула Хиггинса

Один из простых способов учесть темп роста компании1 в качестве параметра модели финансового планирования – задать его в виде постоянной величины, влияющей на значения прочих параметров. Несмотря на кажущуюся простоту, этот подход позволит смоделировать сценарии при различных, хотя и постоянных во времени темпах роста. Например, на протяжении 5 лет компания будет иметь темп роста, равный 10 процентам в год. Однако фиксированное значение темпа роста как параметра модели уменьшает ее «отзывчивость» на изменения прочих характеристик. В результате может возникнуть ситуация, когда заданное постоянное значение темпа роста не позволяет компании оперировать в рамках определенных допущений.

Впервые вопрос об устойчивом темпе роста продаж был поднят Робертом Хиггинсом (Robert C. Higgins) в 1977 году в статье [1]. Он исследовал, какую скорость роста объема продаж (Sustainable Growth Rate – SGR) может поддерживать компания при заданных ограничениях на объем эмиссий акций, объем заимствования и при заданном уровне дивидендных выплат. Хиггинс предложил уравнение для устойчивого темпа роста:

g s

P m ( 1 - d )( 1 + L ) t s — P m ( 1 — d )( 1 + L /

где g_s – устойчивый темп роста продаж;

P_m – чистая прибыльность продаж (чистая прибыль / выручка от реализации продукции);

d – коэффициент дивидендных выплат, то есть доля чистой прибыли, направленная на дивиденды;

L – коэффициент «квоты собственника», отношение задолженности к акционерному капиталу;

t_s – отношение совокупных активов к выручке от реализованной продукции.

Таким образом, финансовая модель планирования может содержать обоснованное значение устойчивого темпа роста продаж, которое зависит от прибыльности продаж, коэффициента «квоты собственника» и отношения активов к выручке от реализованной продукции. Этот подход позволяет связать стратегии инвестирования, финансирования и дивидендную политику в силу того, что каждая из них зависит от скорости роста объема продаж компании.

Разницу между фактическим темпом роста выручки и устойчивым значением этого показателя по Хиггинсу можно определить как SGC (Sustainable growth challenge)²:

( Re venue, )

SGC = In -------- t- - g_s, (2)

( Re venuet-1 J где SGC – разница между фактическим и устойчивым темпами роста выручки;

Revenue_t – фактическая величина выручки в период времени t ;

Revenue_t _{– 1} – фактическая величина выручки в период времени t – 1;

g _s – величина устойчивого темпа роста, рассчитанного по формуле (1).

В случае когда продажи предприятия спрогнозированы в соответствии с моделью Хиггинса, SGC стремится к нулю. Этого можно добиться путем увеличения или уменьшения g_s , а именно финансовых параметров, влияющих на него. Например, молочное хозяйство желает увеличить поголовье скота, продуктовый магазин – ассортимент молока, а завод по производству автомобилей – количество станков. Во всех этих случаях сопутствующей задаче увеличения выручки от реализации является задача увеличения рентабельности производства (уменьшения стоимости продукции), уменьшения издержек, увеличения оборачиваемости активов и финансового рычага.

Для подтверждения практической применимости формулы Хиггинса автор предлагает обратиться к работе [3]. В ней группа исследователей анализировала данные за период 1995–2001 годы по 251 сельскохозяйственной ферме штата Иллинойс, США. Отбор этих хозяйств производился более чем из 7 000 ферм по наиболее успешным финансовым результатам за тот же период. Данные таблицы 1 свидетельствуют о том, что компании в действительности придерживались темпов роста, очень близких к устойчивому темпу роста выручки по модели Хиггинса. Особенно это хорошо показывает анализ зерновых хозяйств, где разница составляет менее 0,1 процента.

Малое отличие фактических темпов роста выручки у эффективных хозяйств от устойчивого темпа роста говорит о практической применимости концепции Хиггинса.

Таблица 1

Значение финансовых показателей и темпов роста в период 1995–2001 годы

Показатель	Все фермы	Зерновые хозяйства	Молочные фермы
Количество ферм	251	197	54
Рентабельность	0,15	0,16	0,13
Оборачиваемость активов	0,26	0,26	0,26
Финансовый рычаг	1,89	1,77	2,33
Коэффициент удержания прибыли, %	43,96	40,66	56,01
Годовой рост выручки, %	4,64	3,42	9,06
SGC , %	-0,39	-0,07	-1,57
g_s , %	5,03	3,49	10,63

3. Модель финансового планирования Уоррена – Шелтона

Наше знакомство с инструментами финансового планирования начнем с модели Уоррена – Шелтона (Warren, Shelton), представленной в 1971 году в статье [4]. Эта модель основана на системе алгебраических уравнений и не решает задач оптимизации. Созданный автором настоящей статьи инструмент финансового планирования для реализации этой модели назовем ФинМод. Модель Уоррена – Шелтона представляет собой средство обеспечения менеджеров необходимыми данными для принятия правильных управленческих решений. Это позволяет руководителям предприятий проигрывать различные варианты развития ситуации при определенных допущениях и изменении таких независимых параметров, как объем продаж, уровень нераспределенной прибыли, соотношение долга и акционерного капитала.

Модель Уоррена – Шелтона связывает воедино разные составляющие менеджмента: инвестиционную, финансовую, производственную и дивидендную политики в виде 19 уравнений, приведенных в таблице 2. Решением этой системы и является разработанный автором инструмент ФинМод. Уравнения, описывающие модель, делятся на подгруппы, соответствующие данным о продажах, инвестициях, финансировании и доходности акции. Поскольку система уравнений Уоррена – Шелтона (см. табл. 2) является достаточно сложной, мы лишь поверхностно рассмотрим ее ключевые особенности и сразу перейдем к результатам моделирования.

Таблица 2

Система уравнений модели Уоррена – Шелтона

Раздел 1. Вычисление объема продаж (Sales) и дохода до уплаты процентов и налогов (EBIT) за период t :
Sales, = Sales , .,(1 + GSales,) t t — I^х t	(3)
EBIT t = REBIT t Sales t	(4)
Раздел 2. Вычисление суммарной потребности в активах на период t :
CA t = RCA t x Sales t	(5)
FA t = RFA t x Sales t	(6)
A t = CA t + FA t	(7)

Раздел 3. Вычисление потребностей в финансировании для желаемого уровня активов:
CL t = RCL t x Sales , (8)
NF = ( A, - CL - PFDSK ) - ( L .- LR, ) - S - R. .- t ' t t t ' ' t - 1 t ' t t - 1
^- b t { ⁽¹	- T t ) [ EBIT t	- i t -1 ( l , -1 - lr , ) ] - pfdiv , } <⁹>
NF_t + b_t (1 - T_t)( i f x NL_t + U_t x NL_t ) = NL_t + NS , (10)
L t = L t -	- LR_t + NL_t (11)
S t = S t-	i - NS t	(12)
R t = R t	-1 + b t [ ( 1 - T t )( EBIT t - i t x L t - U t x NL t ) - PFDIV t ] (13)
	f l , 1 - lr , )	. ML
i_t = i_t 1		+ ie---^L (14)
	I ^Lt J	t L ,
	L_t
K = t _St	- R t	(15)
Раздел 4. Вычисление показателей в расчете на акцию за период t :
EAFCD t = (1 - T_t )( EBIT t - i_tL_t - U , x NL t ) - PFDIV t (16)
CMDIV t = (1 - b_t )EAFCD_t (17)
NUMCS, = NUMCS, - + NEWCS, (18) t t - 1 t
P t = m t	x EPS_t	(19)
	EAFCD_t
EPS_t =		(20)
	NUMCS_t
	CMDIV
DPS , =	^t	(21)
	NUMCS

Разобраться в многочисленных параметрах системы поможет таблица 3, в которой даны определения каждого параметра и момент времени, к которому он относится.

Параметры модели Уоррена – Шелтона

Таблица 3

№ п/п	Параметр	Период времени	Расшифровка
НЕИЗВЕСТНЫЕ ПАРАМЕТРЫ
1	Sales	t	Объем продаж
2	CA	t	Текущие активы
3	FA	t	Постоянные активы
4	A	t	Всего активов
5	CL	t	Кредиторская задолженность
6	NF	t	Потребность в средствах
7	EBIT	t	Доход до выплаты процентов и налогов
8	NL	t	Поступления от нового долга
9	NS	t	Поступления от новых акций

10	L	t	Совокупная задолженность
11	S	t	Обыкновенные акции
12	R	t	Нераспределенная прибыль
13	I	t	Процентная ставка по долгу
14	EAFCD	t	Прибыль, из которой можно выплачивать дивиденды
15	CMDIV	t	Дивиденды по обыкновенным акциям
16	NUMCS	t	Число размещенных обыкновенных акций
17	NEWCS	t	Число эмитированных обыкновенных акций
18	P	t	Курс акции
19	EPS	t	Прибыль на акцию
20	DPS	t	Дивиденды на акцию
ИСХОДНЫЕ ПАРАМЕТРЫ
21	SALES	t – 1	Объем продаж за предыдущий период
22	GSales	t	Рост продаж
23	RCA	t	Оборотные активы в процентах к продажам
24	RFA	t	Постоянные активы в процентах к продажам
25	RCL	t	Кредиторская задолженность в процентах к продажам
26	PFDSK	t	Привилегированные акции
27	PFDIV	t	Дивиденды по привилегированным акциям
28	L	t – 1	Долг за предыдущий период
29	LR	t	Погашение долга
30	S	t – 1	Обыкновенные акции в предыдущий период
31	R	t – 1	Нераспределенная прибыль в предыдущий период
32	b	t	Коэффициент реинвестирования
33	T	t	Средняя ставка налога
34	i	t – 1	Средняя процентная ставка за предыдущий период
35	i^e	t	Ожидаемая процентная ставка по новому долгу
36	REBIT	t	Операционный доход в процентах к продажам
37	U^e	t	Расходы на размещение долга
38	U	t	Расходы на размещение акций
39	K	t	Отношение долга к акционерному капиталу
40	NUMCS	t – 1	Число размещенных акций за предыдущий период
41	m	t	Отношение курса акций к доходу на акцию

Обратим особое внимание на независимую переменную роста продаж ( GSales_t ), которая входит в уравнение (3) в таблице 2. Исходя из системы уравнений Уоррена – Шелтона видно, что абсолютный объем продаж возрастает с увеличением параметра GSales_t на каждом шаге. Однако, как мы уже говорили в разделе 2 настоящей статьи, фиксированное значение этого параметра уменьшает степень свободы модели и тем самым ограничивает применимость этого инструмента на практике. Не будем делать акцент на остальных уравнениях системы, так как это не является целью настоящей статьи. Если читателю необходимо ближе познакомиться с ней, то это можно сделать в соответствующей литературе [4].

Перейдем к практической применимости модели Уоррена – Шелтона на примере ком- пании Exxon Mobil Corporation3. Для этого воспользуемся информацией о финансовых результатах этой компании за 1984 год [4] (см. табл. 4).

Таблица 4

Исходные параметры модели

Параметр	Исходное значение	Номер переменной в соответствии с таблицей 3	Начальный период, год	Конечный период, год
Продажи ( Sales ), у. е.	2 348,6800	1	1984	1984
Акционерный капитал ( S ), у. е.	231,5130	11	1984	1984
Нераспределенная прибыль ( R ), у. е.	723,5800	12	1984	1984
Процентная ставка по долгу ( i ), %	12,50	34	1984	1984
Число акций ( NUMCS) , шт.	44,6730	40	1984	1984
Количество лет в модели	3	Эта переменная в таблице 3 отсутствует	1984	1984
Долгосрочный долг ( L ), у. е.	1 104,3660	28	1984	1984
Рост продаж ( GSales ), %	3,50	22	1985	1987
Оборотные активы / продажи ( RCA ), %	43,70	23	1985	1987
Постоянные активы / продажи ( RFA ), %	94,49	24	1985	1987
Текущие пассивы / продажи ( RCL) , %	37,70	25	1985	1987
Доход до выплаты процентов и налогов / продажи ( REBIT) , %	18	36	1985	1987
Погашение долга в 1-м году ( LR ), у. е.	1,6250	29	1985	1985
Погашение долга во 2-м году ( LR ), у. е.	22,9070	29	1986	1986
Погашение долга в 3-м году ( LR ), у. е.	18,2470	29	1987	1987
Привилегированные акции ( PFDSK ), у. е.	298,8080	26	1985	1987
Дивиденды на привилегированные акции ( PFDIV ), у. е.	19,2900	27	1985	1987
Коэффициент реинвестирования ( b ), ед.	0,40	32	1985	1987
Коэффициент «квоты собственника» ( K ), ед.	1,11	39	1985	1987
Коэффициент «кратное прибыли» ( DPS ), ед.	12,00	20	1985	1987
Ставка налога ( T ), %	46	33	1985	1987
Процентая ставка по новому долгу ( i^e )	12	35	1985	1987
Расходы на размещение долга ( U^e ), %	1,5	37	1985	1987
Расходы на размещение акций ( U ), %	2	38	1985	1987

³ Американская компания Exxon Mobile Corporation – крупнейшая частная нефтяная компания, одна из крупнейших корпораций в мире по размеру рыночной капитализации.

Применив модель ФинМод с использованием заданных в таблице 4 значений, получаем прогноз балансового отчета, отчета о доходах и расходах на период 1984–1987 годы. Эта информация приведена в таблице 1П Приложения. Результаты моделирования позволяют сделать множество выводов, например о наличии потребности в инвестиционных средствах или о влиянии выбранной стратегии развития на стоимость компании. Однако в нашем случае особое внимание стоит обратить на показатель стоимости акции.

Акции компании Exxon Mobile Corporation торгуются на Нью-Йоркской фондовой бирже (NYSE) с 1920 года и на момент написания статьи имеют вес в NYSE Composite Index (NCI) вместе с другими компаниями газовой и нефтедобывающей отрасли в размере 15,61 процента, уступая первое место лишь финансовым институтам. Кроме общего индекса NYSE Composite Index, Exxon Mobile Corporation входит в самый крупный отраслевой индекс Нью-Йоркской фондовой биржи (энергетический) NYSE Energy Index. При этом весовой коэффициент Exxon в этом индексе составляет более 15 процентов (почти одна шестая часть). Это говорит о том, что финансовое положение компании Exxon Mobile сильно связано с динамикой NYSE Composite Index. Сам индекс как отраслевой индикатор вносит свою составляющую в рыночную стоимость акций Exxon Mobile Corporation.

Возьмем результаты моделирования ФинМод за 1984–1987 годы4 и исторические значения котировок Exxon Mobile Corporation (XOM) на NYSE в тот же период5, чтобы понять, насколько точно модель ФинМод прогнозирует рыночную стоимость акции (см. рис. 1).

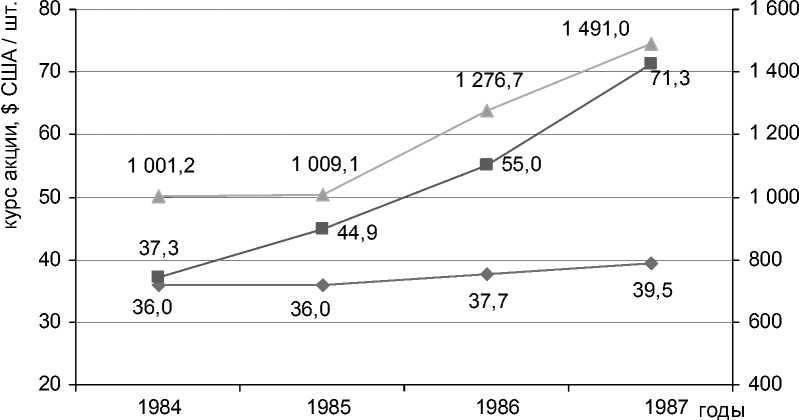
курс акции Exxon Mobile Corp. по модели ФинМод курс акции Exxon Mobile Corp. на фондовой бирже NYSE (XOM)

значение ин декса NYSE Composite Index

Рис. 1. Значения котировок акций Exxon Mobile Corporation и фондовых индексов

Правильно решив систему уравнений Уоррена – Шелтона, мы, к сожалению, не получили качественный прогноз динамики курса акций на период 1985–1987 годы. Смоделированное значение не получило той возрастающей динамики, которая на самом деле наблюдалась у Exxon Mobile. Рисунок 1 отражает лишь плавную динамику роста курса акции, если обратить внимание на результаты модели ФинМод. Автор выделяет две основные причины этого эффекта:

1) как и любая другая модель финансового планирования, ФинМод имеет ряд допущений, а значит, и погрешность прогнозирования; при этом чем больше период планирования, тем больше может оказаться отклонение прогноза от реальности;
2) модель ФинМод не учитывает динамику фондового рынка и эффект его влияния на рыночную стоимость акции компании.

Попробуем разобраться более подробно со вторым пунктом, объясняющим отклонение прогнозных показателей от реальных значений.

В модели ФинМод мы предполагали, что уровень роста выручки будет неизменным на протяжении всего прогнозного периода. Для моделирования мы использовали значение GSales = 3,5%. Следующим шагом будет внедрение в модель ФинМод концепции устойчивого темпа роста, описанной Хиггинсом. Хиггинс вывел формулу устойчивого темпа роста выручки без негативных финансовых последствий, которую мы уже обсудили в разделе 2 настоящей статьи. Напомним ее:

= P m ( 1 - d )( 1 + L )

^gs t s — P m ( 1 — d )( 1 + L /

В обозначениях модели ФинМод формулу (1) можно переписать следующим образом:

d = 1 - b g = Pm (1 - d )(1 + L)

g s t s — P m ( 1 — d )( 1 + L )

P m = REBIT t s = RCA + RFA L = K

REBIT x b ( 1 + K ) ----------------------------= GSales . RCA + RFA - REBIT x b ( 1 + K )

Таким образом, для модели ФинМод-2 ⁶ можно выписать следующую систему:

Система Уоррена - Шелтона ( таблица 2, уравнения 2 - 21)

GSales =

REBIT x b (1 + K )

RCA + RFA - REBIT x b (1 + K )"

Подставив известные параметры модели ФинМод-2 в формулу (3), можно рассчитать GSales = g_s . Данные для компании Exxon Mobile Corporation приведены в таблице 4: REBIT = 18%, b = 40%, K = 111%, RCA = 43,7%, RFA = 94,4%. Рассчитаем значение формулы (3):

= GSales =

0,18 x 0,40 x (1 + 1,11)

0,437 + 0,944 - 0,18 x 0,40 x (1 + 1,11)

= 12,36%.

Как видно из расчетов, темп роста в соответствии с моделью Хиггинса применимо к модели ФинМод-2 равен 12,36 процента на всем протяжении прогнозного периода. Величина GSales является постоянной, так как в модели ФинМод все параметры, влияющие на GSales, тоже являются константами. Обратим внимание на то, что рассчитанное значение темпа роста gs примерно в 4 раза больше того, которое мы принимали в модели ФинМод (GSales = 3,5%). Очевидно, что такое отличие параметров отразится и в результатах прогнозирования по моделям ФинМод и ФинМод-2. Прогноз балансового отчета, отчета о доходах и расходах на прогнозный период представлен в таблице 2П Приложения.

5. Учет рыночной динамики в модели ФинМод

В разделах 2–4 настоящей статьи мы уже реализовали модель Уоррена – Шелтона при некоторых допущениях, а также усовершенствовали ее, задав устойчивый темп роста продаж с помощью формулы Хиггинса. При этом темп роста продаж остается постоянным на протяжении периода моделирования.

Теперь попробуем учесть в модели связь некоторых финансовых показателей с рыночной динамикой. Одним из способов сделать это является внедрение в модель ФинМод-2 прогноза котировок акций компании с учетом поведения фондовых индексов. Для начала разберемся, что влияет на рыночную стоимость акции. Во-первых, рыночные тенденции, связанные с конкретной отраслью. Например, цена на нефть напрямую влияет на рыночную капитализацию компании нефтедобывающих и перерабатывающих отраслей. Во-вторых, деятельность само ́ й компании, ее финансовые показатели и результаты операционной деятельности являются для инвесторов и аналитиков важнейшими показателями определения рыночной стоимости акции. Модели ФинМод и ФинМод-2 охватывают лишь второй фактор, однако рыночные тенденции вообще не учтены в этих моделях. Стоит отметить, что далеко не для всех компаний наблюдается существенная связь между поведением фондового рынка и котировкой акции компании на нем. Если мы говорим о больших корпорациях, таких как Exxon Mobile Corporation, то очевидно, что подобного рода связь существует. Однако для небольших предприятий не «первого эшелона» вряд ли прослеживается такая закономерность. В случае Exxon Mobile Corporation необходимо внести общерыночную корректировку в модель ФинМод-2.

Сравним результаты прогнозирования курса акции, полученного с использованием модели ФинМод (см. табл. 5), исторические значения индекса NYSE Composite Index и котировки Exxon Mobile Corporation (XOM) на NYSE за период 1984–1987 годы7.

Таблица 5

Прогнозные и исторические значения котировок акций Exxon Mobile Corp. и NYSE Index Composite

Значение котировок на первый торговый день календарного года, $ США / 1 шт.	Год
	1984	1985	1986	1987
Курс акции Exxon Mobile Corp. по модели ФинМод	36,0	36,0	37,7	39,5
Курс акции Exxon Mobile Corp. на фондовой бирже NYSE (XOM)	37,3	44,9	55,0	71,3
Значение индекса NYSE Composite Index	1 001,2	1 009,1	1 276,7	1 491,0

Заметим, что прогнозная котировка акции на 1985 год в размере 36,0 доллара США за 1 штуку уже имеет отклонение от исторических значений в тот же момент, так как модель ФинМод была построена на основании фактических данных 1984 года. Из этого сравнения можно сделать вывод, что учет общерыночной динамики является важным элементом прогнозирования. Кроме того, хотелось бы отметить два существенных факта:

1) прогнозирование поправки к курсу акции, отражающей общерыночную динамику, будет строиться на основе оценки фондового индекса, так как прогнозируя котировки акции компании, мы учтем ненужную нам волатильность, финансовые ошибки и потенциальные неудачи само ́ й компании;
2) в настоящей статье использован достаточно примитивный подход к прогнозу индекса и акции, однако он отражает преимущества концепции применения подобного рода поправки, которые описаны в разделе 6. Выбор же способа прогнозирования в каждом конкретном случае, замена его на более сложные и точные методы, остается на усмотрение читателя и выносится за рамками настоящей статьи.

Для того чтобы «настроить» модель, скорректируем стоимость акции в первом периоде ( m 0 ^* ):

XOM 37,5

m_n = m_n----- ¹⁹⁸⁴ = 12,0 x —— = 12,42,

00P1984 , 36,0 , , где P1984 – значение курса акции в модели ФинМод в 1984 году;

XOM ₁₉₈₄ – историческое значение курса акции компании Exxon Mobile Corporation в 1984 году.

Задав начальное значение отношения курса акции к доходу ( m ₀^* = 12,42 ед.), мы тем самым «настроили» модель в начале прогнозного периода (1984 год) на значение, которое описывает фактическую ситуацию на фондовом рынке в этот момент. Далее необходимо сделать поправку на рыночную составляющую роста курса акции. Чтобы это осуществить, подсчитаем β_XOM – коэффициент бета для акций Exxon Mobile Corporation относительно индекса NYSE Composite Index ( NCI ). В общем виде расчет β_XOM выглядит следующим образом:

P xom =

^CovXOM , NCI

^ NCI ²

где Cov_{XOM, NCI} – ковариация относительного приращения индекса и относительного приращения цены акции;

σ _NCI – стандартное отклонение для относительного приращения индекса.

Для расчета коэффициента β_XOM воспользуемся историческими значениями индекса NYSE Composite Index за период 1974–1984 годы и котировками акций Exxon Mobile Corporation за тот же период. Опуская математические расчеты, приведем результат. По состоянию на конец 1984 года коэффициент β_XOM = 1,14.

Для расчета прогнозных показателей индекса воспользуемся линейным приближением, построенным методом наименьших квадратов (далее – МНК). Стоит особо отметить, что в общем случае необходимо применять более сложный метод прогнозирования, в котором учитываются композиция тренда, сезонные составляющие и другие факторы. В нашем случае статистикой будут служить исторические котировки и значения индекса в период 1974–1984 годы. Для связи индекса и курса акции воспользуемся следующей формулой:

P i = P i P xOM

A NCI , NCI i ’

где P_i – курс акций в модели ФинМод;

P_i * – скорректированный курс акции, который будет использоваться в дальнейшем.

Учитывая формулу (8), получаем систему уравнений, которую назовем моделью Фин-Мод-3:

Система Уоррена - Шелтона ( таблица 2, уравнения 2 - 18,20 - 21)

GSales =

REBIT х b (1 + K )

RCA + RFA - REBIT x b (1 + K )

P i = P i P xOM

A NCI i NCI_i

Рассчитаем курс акций с применением предложенного подхода (см. табл. 6).

Таблица 6

Расчет скорректированного значения курса акций Exxon Mobile Corporation c учетом рыночной составляющей

Значение курса акций	Год
Значение курса акций	1984	1985	1986	1987
Прогноз NCI по МНК	1 001,23	1 078,43	1 127,10	1 175,77
β XOM	1,14	1,14	1,14	1,14
Курс акции Exxon Mobile Corp. по модели ФинМод, скорректированной на m *, $ США/1 шт.	37,25	37,25	38,99	40,91
Курс акции Exxon Mobile Corp. по модели ФинМод-3, $ США/1 шт.	37,25	45,74	49,45	54,65

Как показано на рисунке 2, модель ФинМод-3 отражает динамику роста фондового рынка в курсе акции (в отличие от модели ФинМод-2) тем самым приближая прогнозные

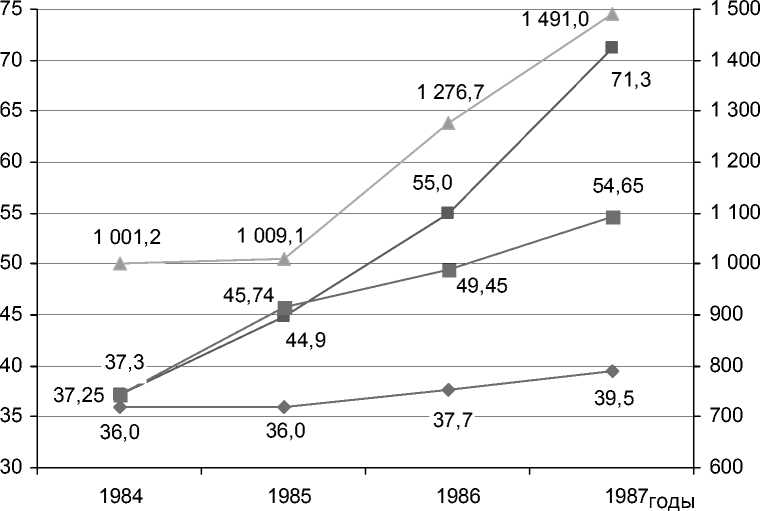
курс акции Exxon Mobile Corp. по модели ФинМод курс акции Exxon Mobile Corp. на фондовой бирже NYSE (XOM)

курс акции Exxon Mobile Corp. по модели ФинМод-3

значение индекса NYSE Composite Index

Рис. 2. Значение фактических и прогнозных котировок акций Exxon Mobile Corporation за период 1984–1987 годы значения к действительным. То есть полученная модель ФинМод-3, способна прогнозировать финансовые показатели не только на основании бухгалтерской информации, но и с учетом рыночных тенденций, улучшая тем самым точность прогнозирования. Этот факт особенно важен, так как показатели курса акций, дохода на 1 акцию и выплачиваемые дивиденды являются инвестиционными критериями, а значит, принципиальными для построения долгосрочных финансовых стратегий.

6. Выводы

В статье представлен разработанный автором комплексный инструмент финансового анализа – модель ФинМод-3. Показана ее практическая применимость. Главное внимание обращено на прикладное значение рассматриваемых методов (модификаций модели ФинМод) и экономическое истолкование получаемых значений. Представленный инструмент повышает эффективность анализа информации и делает более прозрачной связь принимаемых решений с результатами деятельности компании. Полученные данные можно использовать при принятии управленческих решений, разработке бизнес-планов, а также для оценки стоимости предприятия с использованием доходного подхода (метода дисконтирования денежных потоков).

В модели ФинМод-3 рассчитывается устойчивый темп роста объема продаж, а также учитывается рыночная информация для моделирования котировок акций компании. С помощью разработанного инструмента можно получить более точный, чем по каноническим моделям, финансовый прогноз, что подтверждено автором в статье.

В итоге автором построены три разных по сложности и качеству прогнозирования модели, причем возможно их дальнейшее усовершенствование. Каждая из них имеет свою область применимости и набор допущений, однако в совокупности они дают возможность прогнозировать деятельность компании во многих ситуациях.

Несколько слов о технической реализации моделей автором статьи. Расчетная часть, построение диаграмм и отчетов были осуществлены в Microsoft Excel 2003. Особую сложность вызывают системы уравнений Уоррена – Шелтона (см. табл. 2), представленные в виде системы нелинейных уравнений с 6 и 4 неизвестными. Их численное решение производилось с помощью математического пакета Maple 9.5 компании Waterloo Maple Inc, однако существуют и аналитические методы решения этих уравнений. В случае появления вопросов по технической реализации моделей автор готов дать исчерпывающие ответы и объяснения.

ПРИЛОЖЕНИЕ

Таблица 1П

Результаты планирования деятельности Exxon Mobile Corporation за период 1984–1987 годы с применением модели ФинМод

Параметр	Описание параметра	Год
Параметр	Описание параметра	1984	1985	1986	1987
SALES	Объем продаж, у. е.	2 348,68	2 430,88	2 515,96	2 604,02
GSALS	Рост продаж	–	0,035	0,035	0,035
RCA	Текущие активы в процентах к продажам	–	0,437	0,437	0,437
RFA	Постоянные активы в процентах к продажам	–	0,944	0,944	0,944

		Подписка в любое время (495) 974-1945, 974-1950				43

RCL	Кредиторская задолженность в процентах к продажам	–	0,377	0,377	0,377
PFDSK	Привилегированные акции, у. е.	–	298,808	298,808	298,808
PFDIV	Дивиденды по привилегированным акциям, у. е.	–	19,290	19,29	19,29
L	Долгосрочный долг, у. е.	1 104,36	1 126,72	1 171,66	1 218,17
LR	Погашение долга, у. е.	–	1,62	22,90	18,24
S	Обыкновенные акции, у. е.	231,51	235,16	217,30	198,61
R	Нераспределенная прибыль, у. е.	723,58	779,90	838,25	898,84
b	Коэффициент реинвестирования	–	0,40	0,40	0,40
T	Средняя ставка налога, у. е.	–	0,46	0,46	0,46
i	Средняя процентная ставка	0,1250	0,1249	0,1246	0,1244
i e	Ожидаемая процентная ставка по новому долгу	–	0,12	0,12	0,12
REBIT	Операционный доход в процентах к продажам (доход до выплаты процентов и налогов)	–	0,18	0,18	0,18
U ^e	Расходы на размещение долга, у. е.	–	0,015	0,015	0,015
U	Расходы на размещение акций, у. е.	–	0,02	0,02	0,02
K	Отношение долга к акционерному капиталу (коэффициент «квоты собственника)	–	1,11	1,11	1,11
NUMCS	Число размещенных акций, шт.	44,67	46,93	58,34	45,97
m	Отношение курса акций к доходу на акцию	–	12,00	12,00	12,00

Таблица 2П

Результаты планирования деятельности Exxon Mobile Corporation за период 1984–1987 годы с применением модели ФинМод-2

Параметр	Описание параметра	Год
Параметр	Описание параметра	1984	1985	1986	1987
SALES	Объем продаж, у. е.	2 348,68	2 638,98	2 965,17	3 331,68
GSALS	Рост продаж	–	0,1236	0,1236	0,1236
RCA	Текущие активы в процентах к продажам	–	0,437	0,437	0,437
RFA	Постоянные активы в процентах к продажам	–	0,944	0,944	0,944
RCL	Кредиторская задолженность в процентах к продажам	–	0,377	0,377	0,377
PFDSK	Привилегированные акции, у. е.	–	298,808	298,808	298,808
PFDIV	Дивиденды по привилегированным акциям, у. е.	–	19,29	19,29	19,29
L	Долгосрочный долг, у. е.	1 104,36	1 236,64	1 408,92	1 602,50

LR	Погашение долга	–	1,625	22,907	18,247
S	Обыкновенные акции, у. е.	231,51	329,30	415,26	511,21
R	Нераспределенная прибыль, у. е.	723,58	784,78	854,03	932,48
b	Коэффициент реинвестирования	–	0,40	0,40	0,40
T	Средняя ставка налога, у. е.	–	0,46	0,46	0,46
i	Средняя процентная ставка	0,125	0,1245	0,1238	0,1233
i ^e	Ожидаемая процентная ставка по новому долгу	–	0,12	0,12	0,12
REBIT	Операционный доход в процентах к продажам (доход до выплаты процентов и налогов)	–	0,18	0,18	0,18
U e	Расходы на размещение долга, у. е.	–	0,015	0,015	0,015
U	Расходы на размещение акций, у. е.	–	0,020	0,020	0,020
K	Отношение долга к акционерному капиталу (коэффициент «квоты собственника»)	–	1,110	1,110	1,110
NUMCS	Число размещенных акций, шт.	44,673	47,35	49,26	51,37
m	Отношение курса акций к доходу на акцию	–	12,00	12,00	12,00

Статья научная