Моделирование физических и химических явлений в процессах обработки поверхностей материалов высокоэнергетическими источниками

In this paper the traditional conceptions and some effects concerned with irreversible processes models are described. The possibilities of the surface treatment model taking into account the previously applied powdered layer shrinkage and the model of carbon diffusion between covering and substrate in the cooling down condition are presented in a short way.

Под высокотемпературными технологическими процессами зачастую понимают такие технологические процессы, которые реализуются при использовании концентрированных источников энергии. Типичными примерами высокотемпературных технологических процессов являются лазерная и электронная технологии сварки, резки, термической обработки; дуговая сварка и другие способы соединения материалов; плазменные технологии нанесения покрытий и поверхностной обработки; ионные технологии; кислородная резка; совмещенные технологии резки, сварки, наплавки; процессы получения тонких пленок и выращивание монокристаллов; процессы химической и диффузионной обработки поверхностей материалов и др. К высокотемпературным технологиям можно отнести и многие технологии получения новых материалов в химической промышленности; переработки и сжигания природного топлива; различные металлургические процессы. Каждый из названных технологических процессов, в свою очередь, включает множество частных технологий, зависящих от конкретного технического решения, условий и материалов, для которых процесс предназначен. Современные методы обработки поверхностей и нанесения покрытий связаны с преобразованием различных видов энергии в тепловую, с процессами нагрева и охлаждения и разнообразными сопутствующими явлениями, которые и приводят к изменению состава, структуры и свойств обрабатываемых слоев. Преобразования структуры в высокотемпературных технологических процессах происходят на разных стадиях, включают различные уровни (мезо-, микро- и нано-) и зависят от разнообразных физических явлений, которые характеризуются разными масштабами и протекают совместно. Традиционно математическое моделирование в этой области сводится к расчету формы эффективных источников энергии, процессов плавления и кристаллизации в условиях высокоэнергетических воздействий, явления распыления поверхностного слоя или гидродинамики расплавов. Но формирование структуры и свойств поверхностных слоев происходит непосредственно в процессе обработки и является следствием разнообразных необратимых физико-химических процессов, не учитываемых в традиционных моделях. На традиционных представлениях, некоторых эффектах, связанных с учетом в моделях необратимых процессов, а также на описании возможностей этих моделей мы далее и остановимся.

Эффективный источник тепла

Число способов модификации поверхностей велико, каждый из них имеет свои особенности (рис. 1). Более того, под общим названием скрываются различные технологические модификации. Тем не менее технологические процессы поверхностной обработки высокоэнергетическими источниками имеют ряд общих черт, что и послужило в свое время базой для развития теплофизических основ этих процессов. Для всех высокотемпературных технологий характерны существенная неравновесность процессов, связанная с неоднородным распределением температуры и ее изменением во времени; высокие скорости нагрева и охлаждения различных элементов системы; наличие сложного теплообмена; существование нескольких различных фаз; соотношение между которыми изменяется; разнообразные физикохимические явления, сопутствующие нагреву и охлаждению или лежащие в основе технологии. Но, в первую очередь, во всех высокотемпературных технологиях происходит преобразование различных видов энергии в тепловую энергию и (или) ее непосредственное использование для получения, переработки и модификации материалов и их поверхностей.

Рис. 1. Упрощенная классификация методов обработки поверхносте й

Использование разных источников, связанных с видами воздействия, приводит к разнообразным задачам теплопроводности с различными начальными и граничными условиями. При анализе тепловых процессов реальные источники заменяют идеализированными, форма которых в той или иной степени приближена к фактической. В зависимости от характера воздействия выделяют источники объемные и поверхностные, неподвижные и движущиеся, распределенные и точечные. Такая классификация является достаточно условной и берет свое начало в задачах сварки и резки [1,2], но может быть использована и для задач поверхностной обработки.

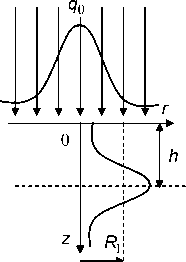
Рис. 2. К определению вида источника

Один и тот же источник энергии может быть отнесен к разным типам. Например, характер распределения энергии в электронном луче может быть описан кривой Гаусса (рис.2) с максимумом в объеме [3]:

q(х, y, z)= qо exp[-(x2 + y 2 )k 1 -(z - h)2 k2 ], где q0 максимальная плотность мощности источника тепла

(определяемая силой тока и разностью потенциалов), k1 – коэффициент сосредоточенности потока электронов (аналогично лазерному излучению), h – положение максимума тепловыделения в объеме материала. Можно определить эффективный радиус электронного луча R1 = VTkT и эффективную область рассеяния энергии или проникновения электронов в объем R2 = 1, 42с.. Тогда при условии хт = К** >> R2, где к = Х/(c р)  - коэффициент температуропроводности, t*  - характерное для технологического процесса время (например, время наблюдения), xT – характерный тепловой масштаб, источник энергии, связанный с электронным лучом, можно считать поверхностным. Это вполне подходит для электронов с энергиями 10–500 Эв, когда плотности мощности не превышают 105 ^ 106 Вт/см2. Но это же совершенно не годится для быстрых электронов, а тем более для релятивистских, энергия которых превышает 1 Мэв.

Если эффективный радиус электронного луча много меньше характерного размера r0 поверхности, на которую он действует, можно говорить о точечном источнике. Если же R1 ~ R0, где Rg - эффективный размер обрабатываемой поверхности, источник тепла становится распределенным, т.е. зависящим от координат.

В технологиях обработки поверхностей материалов, так же, как в процессах сварки и резки, большую роль играют характер перемещения детали и режим сканирования электронного луча [3,4], что приводит к понятию подвижного источника энергии.

Например, при обработке поверхности детали, перемещающейся вдоль оси Ox со

скоростью V , сканирующим электронным лучом (рис.3) часто можно использовать функцию вида (в случае пилообразных колебаний луча)

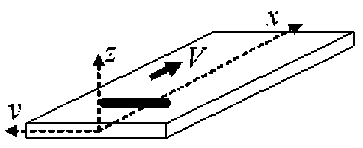
Рис. 3. Движущийся     вдоль поверхности источник тела

f ( x, y , z ) = exp

У 2 + (x — Vt )2

R 1 ²

^{( z} - h ^{) 2}

R 2 ²

| x ^S hx ’

где h_x - полуширина сканирования. Для поверхностного источника h = 0 .

С увеличением сложности характера тепловыделения возрастает и число параметров, необходимых для описания характера воздействия.

Иного вида источники тепловыделения, связанные с внешним воздействием, имеют место в процессах ионной имплантации и плазменного напыления [5].

Геометрия детали

Наряду с характером внешнего воздействия при постановке задач поверхностной обработки материалов большую роль играет геометрия детали [2,6,7]. При формулировке моделей процессов обработки в декартовой системе координат среди тел классических форм выделяют стержни, пластины (параллелепипеды, у которых толщина много меньше ширины и длины) и трехмерные тела. Если речь идет о термической обработке тел вращения (сканирующим электронным лучом, излучением лазера и т.п.), то целесообразно перейти к цилиндрической системе координат. В этом случае уравнение теплопроводности принимает вид cр— = -V- J + q(r, ф, z, t), J =-XVT,

где оt     1 оt     оT            1 о        1 о  r о r

VT a er + д еф + a ez ’ V ' J — a (rJr)+ a JФ + a Jz ’ dr     r дф     dz           r оr       r дф dz

J_r,J ф ,J_z - компоненты вектора плотности теплового потока, e _r ,С ф ,e _z - единичные векторы цилиндрической системы координат; c , р , X - теплофизические характеристики (теплоемкость, плотность и теплопроводность), зависящие от температуры и координат. В общем случае мы приходим к трехмерным задачам теплопроводности. Учет конкретных особенностей технологий позволяет существенно упростить задачу или, наоборот, учесть в ней более «тонкие» вещи.

Например, при термической обработке поверхностным источником энергии боковой поверхности полого цилиндра (рис. 4), внутренняя поверхность которого теплоизолирована, уравнение теплопроводности (1) дополняется граничными условиями (в (1) источник тепла в этом случае отсутствует), r — RV: — = 0,                                   (2)

д r r = R 2: ^^T = q (ф, z-t )-a(T - Te ) ^ S (t 4 - Th )•                          (3)

z — 0 , L :

(иногда требуется учесть теплообмен излучением на внутренней поверхности цилиндра).

В случае цилиндра с покрытием толщиной h мы приходим к сопряженной задаче теплопроводности: уравнение (1) без источника, в котором все величины имеют индекс «1», имеет место для основной детали, а с индексом «2» – для покрытия. Условие (3) с X —X 2 записывается при r — R 2 + h , а при r — R i имеет место условие идеального теплового

” — 0 д z

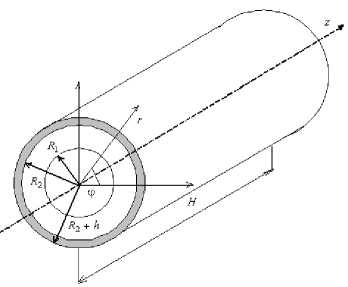
Рис. 4. Схема расчетной области для полого цилиндра

контакта,

~ д T

Xi---- д x

, д T

— X 2 —

R ₂ - 0       ^д x

R 2 + 0

’ ^T R ₂ - 0

^T R ₂ + 0 '

Если покрытие можно считать термически тонким по сравнению с основой, проинтегрируем уравнение (1) по координате r в пределах от R 2 до R 2 + h с учетом условий (3), (5). Тогда придем к задаче, включающей уравнение теплопроводности (1) без источников со свойствами основы ( c , p i , X i ), условия (2), (4) и

X i I T — q ( ф , z , t ) -a ( T - T e ) -a s T ⁴ - c 2 P 2 h ^ T -д r д t

-

h   AfX dT I

( R ₂ + h ) R ₂ дф ( ² дф J

+ h — I X д z (

д T

² a z

Для металлов, обладающих высокой теплопроводностью, представляет интерес еще одно приближение, которое корректно для тонкостенных труб с покрытиями. Интегрируя (i) по всей толщине трубы от Ri до R2 + h, придем к двумерному уравнению д T

[ c i ^p i ^{( R} 2 ^{- R} i ^{) +} c 2 ^p 2 h ]^7 ^— ^“|^X д t   дф^

д t

дt ) дк дt )             x ф - 11 - Xz^"I+ q(t)f(ф,z,t)-CTST v дф J дz V дz J

⁴ -a ( T - T e ) , (7)

где

_{X — X} ^R 2 ^{- R} i +    ^X 2 h

^X z ^—X i ^{( R} 2 ^{- R} i ^)+X 2 h ,

^{ф !} R 2 R i     ( R 2 + h ) R 2

которое, вообще говоря, описывает анизотропный процесс теплопроводности.

Если источник равномерно распределен по толщине цилиндра, что может представлять интерес для плазменных технологий, то от (7) легко перейдем к одномерному уравнению.

Задачам теплопроводности с подвижными и неподвижными источниками тепла, посвящалось и посвящается множество публикаций в журналах ИФЖ, «Теплофизика и аэромеханика», ТВТ, «Сварочное производство», «Heat- and Mass Transfer» и другие, поскольку они имеют широкие приложения в различных областях физики.

Плавление и кристаллизация

Не секрет, что процессы поверхностной обработки материалов высокоэнергетическими источниками сопровождаются, в первую очередь, плавлением материала, а остывание деталей за движущимся источником и после обработки непосредственно связано с его кристаллизацией. Экспериментатору в подобных исследованиях интересны не только величина максимальной температуры, но и размер и форма ванны расплава, размер зоны термического влияния (ЗТВ), достигаемые в тех или иных режимах обработки. С одной стороны, размер ванны расплава можно оценить условно по величине температуры плавления, используя решения задач теплопроводности, в том числе аналитические. Но поглощение тепла в результате плавления может сказаться на всем балансе тепла, на величине максимальной температуры, поэтому необходим учет явлений плавления и кристаллизации в динамике.

Из физики и термодинамики известно, что в окрестности фазовых переходов первого рода теплоемкость вещества резко возрастает, что отражает зависимость

c p =

c_L p_L, T >  T_m         ,      ,

LL m

_T      + ^L m ^p s ⁵⁽ T T m ) ,

. ^cs p s , ^T <  T m

где T_m – температура плавления (кристаллизации), L_m – скрытая теплота плавления, индекс « L » относится к жидкости (к расплаву), индекс « s » - к твердой фазе; 5 ( x ) -дельта-функция Дирака. При численном решении задач теплопроводности с фазовыми переходами дельта-функция заменяется дельта-образной функцией при неизменном энергетическом балансе. Удобной в этом отношении является функция

⁵ i =      exp

sy П

V

T^Tm ]

s )

7 J

,

где s – полуинтервал сглаживания. Экспериментальные данные по теплофизическим характеристикам веществ вдали от температуры плавления аппроксимируются полиномами второй или третьей степени.

В выборе параметров 5 -образной функции существуют свои тонкости, которые необходимо принимать во внимание. Если все сделано корректно, то на температурной кривой в окрестности температуры плавления должно появиться плато, причем оно будет заметно и на кривых температура–время в фиксированных точках, и на пространственных распределениях в различные моменты времени.

В качестве простого примера рассмотрим задачу о термической обработке материала с покрытием при условии малости их общей толщины движущимся источником энергии. Простейшая математическая постановка задачи в этом случае может быть представлена в виде

( X  d T   e L 5 T

^{( C p)} eff д I ^ eff я

О t   Оx V     оx

+ — x

dy V

5 T )

eff Я

sy J

+ q ⁰ f ^{( x} , y , t ) , h ₁

ат            ат

x = 0, Hx : — = 0 , y = 0, Hv : — = 0 , xy dx                dy t = 0: T = To, где

f ( x , y , z ) = exp [ ^- k 1 ⁽ y ² + ⁽ x - Vt ^{) 2} JI x <  h x , h_x - ширина сканирования, H x , H y - размеры пластины в направлениях x и y , h -толщина основы, эффективные теплофизические свойства вычисляются аналогично предыдущему (осредняются по толщине покрытия с основой), а теплоемкости основы C 1 P 1 и покрытия c 2 Р 2 меняются в соответствии с (8).

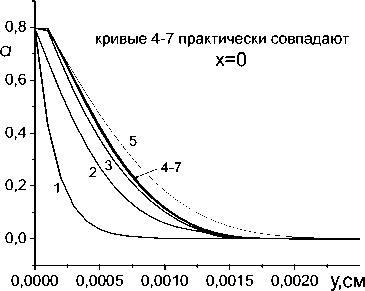
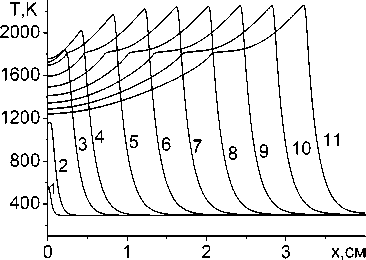
Конечно, эта же модель справедлива, если покрытия нет. Примем в этом случае, что пластина изготовлена из железа ( c 1 s = 0,825, c 1 _L = 0,608 Дж/(ыК), P 1 s = 7 , 61 , P 1 l = 7 , 87 г/см 3 , X i = 0 , 45 Дж (смгсЧО, T mi = 1810 К, L mi = 247 Дж/г). В любом случае через некоторое время после начала движения источника значение максимальной температуры перестает изменяться, что видно из рис. 5, а . Плато на температурных кривых соответствует температуре плавления. Плато имеется на кривой и перед источником, но вследствие большого градиента температуры оно слабо выражено. Кроме максимальной температуры можно построить пространственные распределения, что иллюстрирует рис. 6. Анализируя данные расчетов T ( x , y , t ) , можно исследовать эволюцию ванны расплава и зоны термического влияния (ЗТВ), которую определяют по условно заданной температуре, ниже которой в материале не наблюдается видимых изменений в структуре. Соответствующие рис. 6 форма ванны расплава и ЗТВ показаны на рис. 7 темным и светло-серым цветом. Первая из изолиний на всех рисунках отвечает температуре T = 350 К. Внешний источник движется вдоль оси Ox (как это показано на рис. 3).

а                                         б

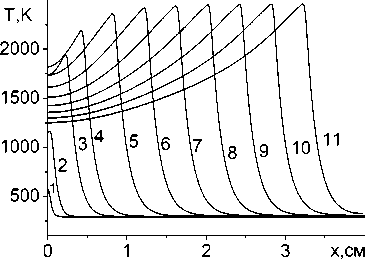
Рис. 5. Распределение температуры вдоль оси движения источника при обработке железной пластины q 0 = 7 • 10 4 Вт/см² с учетом плавления ( а ) и без учета плавления ( б ): t = 1 . - 0 , 02 ; 2 . - 0 , 1 ; 3 . - 0 , 5 ; 4 . - 0 , 9 ; 5 . - 1 , 7 ; 6 . - 2 , 5 ; 7 . - 3 , 3 ; 8 . - 4 , 1 ; 9 . - 4 , 9 ; 10 . - 5 , 7 ; 11 . - 6 , 5

Если плавление явно не учитывается, то можно, конечно, построить границу зоны термического влияния и предположительной ванны расплава, но вследствие того, что величина максимальной температуры теперь стала иной (рис. 5, б ), результаты такого исследования также изменятся. Состав фаз, определенный на основе диаграмм состояния по рассчитанной в тепловой задаче температуре, в любом случае будет весьма приближенным. Дополнительное усложнение тепловых моделей связано с учетом зависимостей теплофизических свойств от температуры, что также приводит к численным изменениям температуры и размеров ЗТВ и ванны расплава.

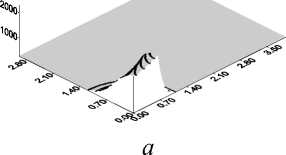
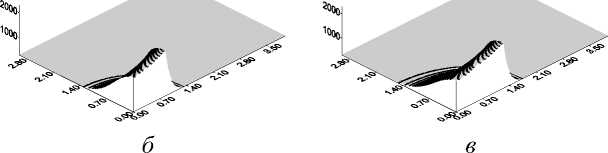
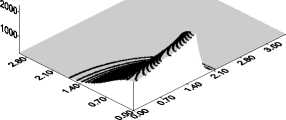
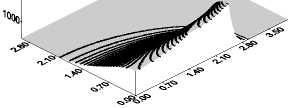
д

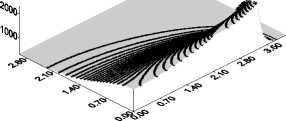
Рис. 6.Эволюция температуры во времени q ₀ = 7 ⋅ 10⁴ Вт/см² при нагреве железной пластины с учетом плавления: t = ( a ) - 1,3; ( б ) - 1,7; ( в ) - 2,5;   ( г ) - 3,3; ( д ) - 4,9; ( е ) - 6,5 с

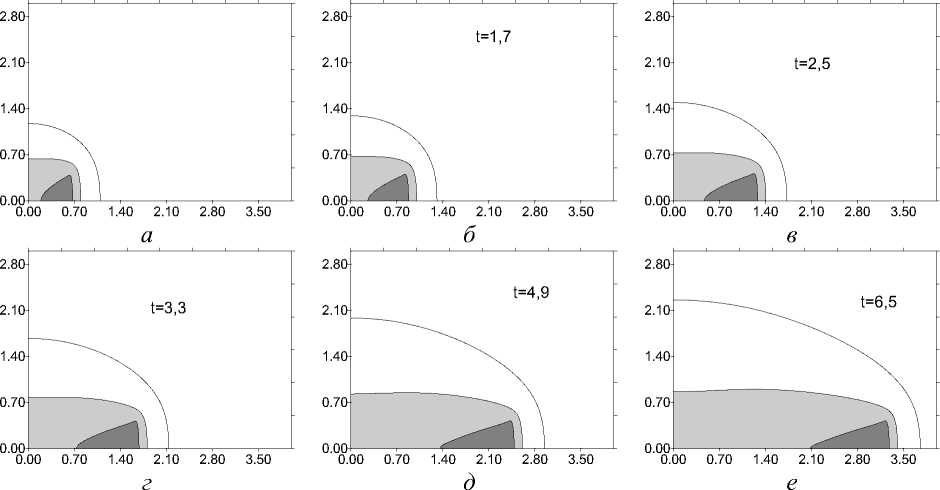
Рис. 6. Эволюция во времени ванны расплава (темно серый цвет) и ЗТВ (светло серый цвет) при нагреве железной пластины с учетом плавления. В незакрашенной области температура изменяется от 900 до 350 К: q ₀ = 7 ⋅ 10⁴ Вт/см² t = ( a ) - 1,3; ( б ) - 1,7; ( в ) - 2,5; ( г ) - 3,3; ( д ) - 4,9; ( е ) - 6,5 с

Если осуществляется нагрев подвижным источником материала с покрытием, то вследствие дополнительных затрат тепла численные значения температуры изменяются. Цель подобных исследований заключается в анализе зависимости максимальной температуры, размеров ванны расплава от толщины и типа покрытия при варьировании технологических параметров.

Это, пожалуй, все, что могут дать чисто теплофизические задачи.

Качественно результаты не изменяются и при переходе к трехмерным моделям. Дополнительные возможности имеются лишь для определения глубины проплавления и распределения температуры вследствие объемного тепловыделения.

Замечу, что при исследовании процессов плавления–кристаллизации появляется класс задач теплопроводности с подвижными границами, который представляет интерес для различных областей физики. Выделение подвижных границ раздела фаз в задачах поверхностной модификации не всегда целесообразно, так как возникающие при этом математические и алгоритмические трудности [8] не стоят получаемых при этом результатов.

В случае неподвижных внешних источников (например, импульсная электронно-лучевая и лазерная обработка) для процессов нагрева и охлаждения тел, в том числе многослойных, в первом приближении подходят классические аналитические методы. Целый ряд полезных для технологий обработки задач теории теплопроводности с решениями содержится, например, в [9–11]. Некоторые из задач воспроизведены в [12,13].

Физико-химические превращения в зоне обработки

Усложнение (усовершенствование) моделей поверхностной обработки может идти по пути учета разнообразных физико-химических явлений, в результате которых и происходит формирование свойств покрытий. В технологиях различного типа явления, лимитирующие формирование свойств, – различны.

Например, в некоторых ситуациях для придания нужных свойств предварительно нанесенному порошковому покрытию требуется термическая обработка, приводящая к уплотнению этого слоя или к усадке. С физической точки зрения усадка связана с процессами плавления и массопереноса в различных фазах, с появлением сил сцепления между отдельными частицами (адгезионной или химической природы). Все эти процессы – термически активируемые и происходят на микро- и мезоуровнях, т.е. в масштабе отдельно взятых частиц: в объеме частиц и на границах их раздела. Макрокинетическое описание процессов, приводящих к усадке, в первом приближении можно свести к поиску кинетического закона, параметры которого зависят от процессов, протекающих на «низших» структурных уровнях.

В рамках представлений, развитых в [14–16], кинетику усадки описывает уравнение dh2 dt

k ₂

(

V 2 min

I p

- 1

J

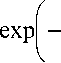
E2- I b •

, 21 >  ⁿmin ;

RT J

10,                              h2 > hmin, t - 0 :   h2 - h20, где h2min – минимально возможная толщина покрытия, k2 – константа скорости усадки, E2 – энергия активации процесса усадки (ее величина определяется процессом, лимитирующим усадку на микроуровне), p – показатель степени в законе усадки, который может быть как целой, так и дробной величиной (зависит, например, от характера поверхностей частиц). Все эти параметры, с одной стороны, – экспериментально определяемые, а с другой – кинетика процессов спекания является очень развитой областью физики, в рамках которой для нахождения кинетических констант можно формулировать и исследовать специальные частные подмодели.

Для иллюстрации дополнительных возможностей, которые появляются в модели процесса поверхностной обработки, предположим, что на поверхность материала, изготовленного из железа (свойства которого выписаны выше), нанесен слой порошка толщиной h 2 = h 20 = 0 , 1 см. Примем его свойства следующими: X 2 = 0 , 08 Вт/(см^К), c 2 , = c 2 L = 1 , 25 Дж/(г-К), Р , 2 = Р L 2 = 3 , 75 г/см³, T m 2 = 2318 К, L m 2 = 389 Дж/г.

Тогда модель (9), (10) в первом приближении позволит описать изменение рельефа поверхности вследствие усадки порошкового слоя в процессе поверхностной обработки. Так, полагая q 0 = 7 - 10 4 Вт/см², получим следующую картину.

Во-первых, температура в этом случае оказывается несколько ниже, чем в предыдущем случае, так как потребовались дополнительные затраты тепла на прогрев покрытия. Во-вторых, температура плавления материала покрытия не достигается, т.е. усадка происходит в «твердой» фазе. В-третьих, иной получается и форма температурных кривых, поскольку эффективные теплофизические характеристики в процессе усадки изменяются:

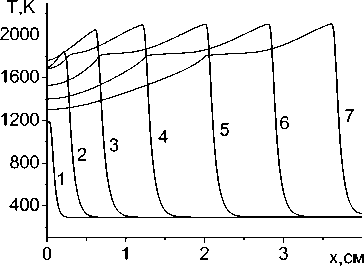
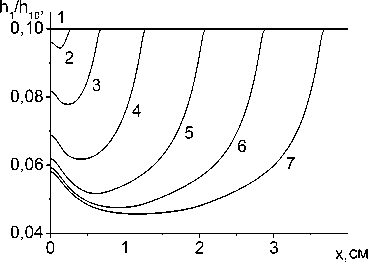
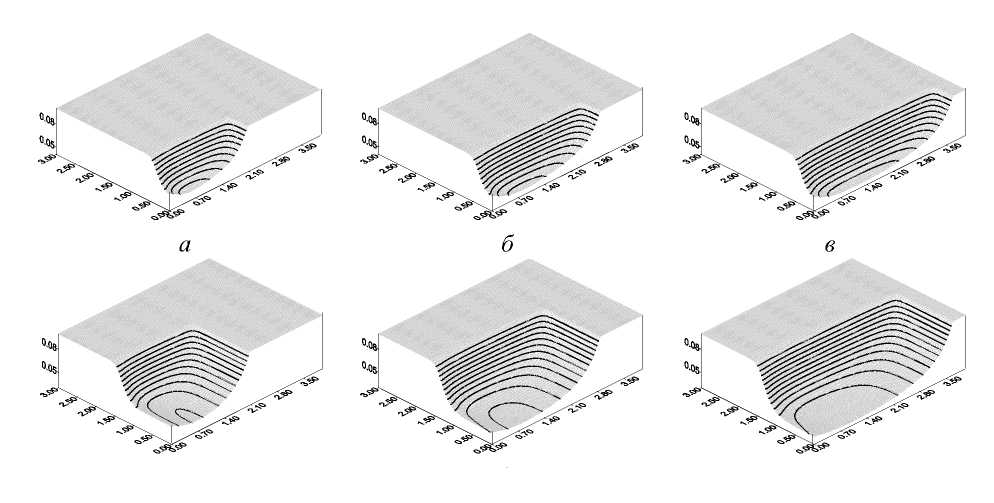
^{( c р)} eff = ^С 1 ^р 1 ⁺ c 2 ^р 2 ^h 2 ⁽ T )/ ^h 1 , ^X eff = ^X 1 ^+X 2 ^h 2 ⁽ T )/ ^h 1 • (H) Изменение рельефа поверхности со временем показано на рис. 7 и рис. 8 где представлены распределения толщины порошкового слоя в различные моменты времени. Видно, что следствием малой по длительности начальной нестационарной стадии процесса обработки является неравномерная толщина покрытия у торца x = 0 . Неравномерная толщина вдоль оси Oy , очевидно, связана с неравномерным нагревом и потерями тепла вследствие теплопроводности. Чтобы выровнять поверхностный слой, требуется многопроходная обработка или большая ширина сканирования, что и используется в технологиях обработки. Влияние ширины сканирования видно из сравнения верхней и нижней строк (рис. 8). Параметры для расчета ( E 2 = 100 Дж/моль, h _2min = 0,03 см, к 2 = 5 - 10² см/с) намеренно выбраны такими, чтобы влияние было наглядным. Наблюдаемая экспериментально усадка может достигать 30–40 %.

а б

Рис. 7. Распределение температуры и толщины покрытия вдоль оси движения источника в различные моменты времени: q 0 = 7 - 10 4 Вт/см², V = 0 , 5 см/с, ^ 1 = 0 , 03, h y = 0 , 05 см

а

б

в

г

д

е

Рис. 8. Толщина покрытия в различные моменты времени. а—в q 0 = 7 - 10 4 , h y = 0 , 5 ; г-е q 0 = 7 - 10 4 , h y = 1 , 5 ; t = а, г - 4,1; б, д - 5,7; в, е - 7,3 с

В трехмерном варианте модели поверхностной обработки с учетом усадки порошкового слоя [15,16] обнаруживаются подобные закономерности. Но для корректного описания наблюдаемых процессов в выбранной системе необходимо учесть перемешивание частиц в расплаве, образующемся под порошковым слоем, и поглощение энергии электронного луча в объеме.

Технология поверхностной обработки сканирующим электронным лучом может существенно отличаться от описанных простых ситуаций. Например, в [17] для модификации поверхностей с целью придания им высоких прочностных свойств используют целенаправленное изменение состава. В формирующуюся ванну расплава подают модифицирующие частицы, химическая природа и свойства которых могут быть различны. Если частицы – инертные и тугоплавкие, то в результате обработки образуется дисперсно-упрочненный поверхностный слой, или фактически композиционное покрытие. Если частицы могут растворяться в расплаве, то в зависимости от технологических параметров после обработки получается либо гомогенное покрытие, либо композиционное, причем состав матрицы также получается различным, что непосредственно связано с процессом растворения. Математические модели для различных вариантов такого процесса обработки, позволяющие предсказывать и описывать эти эффекты, представлены в [18–20] и включают кинетическое уравнение для доли частиц f Ep А

d П p          ,    / \

— = Wp - kpФ(П p )exp где np — объемная доля частиц в расплаве, Wp - источник частиц, а формальнокинетические параметры зависят от конкретной физической ситуации. В теории растворения [21] считается, что энергия активации Ep определяется либо диффузией в расплаве, либо химическими превращениями между частицами и основой, а константа растворения kp целиком зависит от гидродинамической картины течения расплава (в моделях растворения эта зависимость считается известной). Кинетическая функция

ф ( ц p ) опять же определяется процессами, протекающими на микроуровне. Для ее нахождения имеется целый ряд моделей, часть из которых описана в [22, 23].

Частицы оказывают влияние и на эффективные теплофизические свойства, что учитывается в моделях. В случае растворимых частиц изменяется состав матрицы, что приводит к изменению температуры плавления и к необходимости использовать для описания процессов плавления и кристаллизации более сложную теорию (см. раздел 5).

Картина существенно усложняется, если процесс растворения сопровождается химическими реакциями в объеме. Вариант модели для этой ситуации описан в [24].

Существуют технологии поверхностной обработки, сочетающие в себе достоинства энергии электронного луча и синтеза в конденсированной фазе – фактически осуществляется управляемый синтез покрытия на подложке [25]. Организация процесса синтеза также может быть различной. Чисто теплофизические модели здесь более не подходят, и на помощь приходит аппарат макрокинетики [26]. Задача теплопроводности дополняется системой уравнений химической кинетики, а в уравнении теплопроводности появляется слагаемое, учитывающее суммарное тепловыделение в химических реакциях. Модели такого типа позволяют описать эволюцию фазового и химического состава покрытий в ходе обработки, дать состав покрытия к концу процесса, оценить роль химических источников энергии [27–30].

Но даже при таком усложнении (усовершенствовании) моделей ряд реально наблюдаемых явлений остается за кадром.

Перераспределение легирующих элементов

Не секрет, что свойства покрытий и характер их связи с основой зависят от диффузионных процессов различной природы: от перемешивания частиц в расплаве, от диффузии растворенных элементов, от перераспределения примесей в процессах обработки (в ходе нагрева и остывания). Перераспределение элементов приводит к формированию градиентной структуры поверхностного слоя, что важно для придания материалам нужных свойств.

Так, в процессе электронно-лучевой наплавки покрытия с высоким содержанием углерода на подложку из малоуглеродистой стали переходная зона формируется за счет твердофазной диффузии углерода в подложке от поверхности подложка–покрытие. В результате происходит обогащение приграничной области подложки углеродом. При формулировке модели в [31] предполагается, что медленный процесс диффузии углерода из наплавленного покрытия в подложку происходит на стадии остывания покрытия, а перераспределением элементов между слоями непосредственно в ходе наплавки можно пренебречь. Это условие обеспечивается малостью скорости диффузии по сравнению с теплопроводностью в твердых телах.

Пусть после прохождения электронного луча по поверхности обрабатываемого материала ( Fe ) (в процессе нанесения покрытия) на ней остается «дорожка» расплавленного присадочного материала ( Fe + 0,8% C ) , в процессе остывания которого и происходит образование переходной зоны (рис. 9). Полагаем, что в каждом сечении обрабатываемой поверхности, перпендикулярном направлению движения электронного луча, условия формирования диффузионной зоны одинаковы. Процессы распространения тепла и массы (легирующего элемента) в подложке опишем обычными уравнениями теплопроводности и диффузии

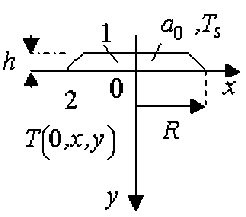
Рис. 9. Иллюстрация к математической постановке задачи: 1 – присадочный материал, 2 – подложка

c P

д T₂    д L д T ₂ ) д

2 =I X 2 1 + д t   дx ( дx ) дy

дai    д f д a ₂ 1   д

2 =| D 2 1 + д t   дx l   дx ) дy

д T c P h    = h д t

-(.- T !

I X д x l д x

fx^ 1 l ^д y )

f д a ₂ 1

_v     - у )"

Полагаем , что толщина слоя присадочного материала h много меньше , чем толщина подложки . Это позволяет не рассматривать распределение температуры и концентрации в нем . Тогда в качестве граничного условия для температуры при y = 0 будет справедливо дифференциальное уравнение

+ Х^1      n,_vJ / .4 - T_e ⁴ ) ,              (14)

>J y =- 0     l ^д У ) y =+ 0

позволяющее определить поток тепла, поступающего в подложку, при этом очевидно

T 1 = T ₂ , y = 0 .

Аналогичные условие имеют место для концентрации легирующего элемента:

h = hf2 D  1   + D f^1   ,(15)

⁵ t    l° x ^{5 x} ) y .- 0     l ⁵ y ) y =+ 0

a i = a 2 .

Ось oy является осью симметрии, поэтому здесь справедливо условие

E^l = 0, Ear = 0, i = 1,2, x = 0.(16)

дxд

На бесконечном удалении от нагретой области источники и стоки тепла и массы отсутствуют,

X,-^ = 0 , D, —2 = 0, i = 1,2, x ^« ;(17)

ii дxд

X2-T2 = 0, D2-O2 = 0, y ^».(18)

д y         д y

Если вдоль оси Оy обрабатываемый образец имеет конечные размеры, то на его поверхности, противоположной нагретой, для температуры ставится условие типа (14) для h=0, а для концентрации легирующего элемента – условие (16).

В начальный момент времени t = 0 имеем a1 = a 0, T1 = Ts; a 2 = 0, T2 = f2 (x, y).                             (19)

В пользу такого приближения говорит и тот факт, что вследствие конвективного перемешивания в процессе наплавки температура расплавленного слоя и концентрация в нем выравниваются.

В (12) - (19) a i - концентрация легирующего элемента, индекс i = 1 относится к слою присадочного материала, индекс i = 2 - к подложке; D - коэффициент диффузии, зависящий в общем случае от температуры и концентрации легирующего элемента, T_e – температура окружающей среды, a ₀ – начальное значение концентрации легирующего элемента в расплаве, T s - его начальная температура; h = h 0 , если | x | <  R , и h = 0 при | x | >  R , R - половина ширины сканирования электронного луча. Остальные обозначения – аналогичны предыдущему.

Начальное значение температуры расплава и начальное распределение температуры в подложке определяются параметрами внешнего источника и могут быть оценены независимо либо на основе данных эксперимента, либо с помощью простейших аналитических зависимостей [3,2].

Эта модель позволяет определить фазовую структуру переходной зоны, распределение концентраций в ней и форму зоны термического влияния, формирующиеся в процессе остывания покрытия и подложки.

В отличие от простейшей модели, описанной выше (в разделе 3 этой статьи), здесь при моделировании процесса плавления использованы представления теории двухфазной зоны [32].

Для теплоемкости, плотности и коэффициента теплопроводности приняты зависимости c = cs '(1 -П) + cL -П + Qd^n , dT

P = Ps "(1 -n)+Pl-П ,                                     (20)

^X =^X s ^-( 1 — ⁿ⁾+X L "ⁿ , где n — доля жидкой фазы, определяемая из соотношения

П = 1 -

T iq — T

n

_v T liq T sol ,

Tliq, Tsol - температуры ликвидуса и солидуса на диаграмме состояния Fe - C [33], n -варьируется для разных сплавов и зависит от содержания примесей; Q – скрытая теплота плавления, индекс " s" - относится к твердому состоянию, 'L' - к жидкости. Температуры ликвидуса Tliq и солидуса Tsol можно аппроксимировать линейными зависимостями

Tsol = as - a + bs , Tliq = al - a + bl ,

Tn -e где bs = bs =e, as = —---, Ul = —L0---, Tsg , Tlo - температуры солидуса и ликвидуса a0

при содержании углерода в стали a g , e - температура плавления (кристаллизации) чистого железа (т.е. для a = 0 ).

В случае плавления чистого железа изменение теплоемкости в окрестности температуры плавления описывается зависимостью, аналогичной (8). Для теплоемкости α-фазы справедливо такое же выражение, включающее свои параметры.

Величины полуинтервала сглаживания и теплоту структурного фазового перехода у ^ а находим, аппроксимируя экспериментальные данные [34] по теплоемкостям в окрестности температуры e i . Имеем:

c _а = 0 , 447 ,    c _Y = 0 , 608 ,    c_L = 0 , 825 Дж/(г.К);   р _s = 7 , 87 ,   p _L = 7 , 61    г/см³;    T_{s g} = 1643 ,

T_{l 0} = 1763 , e = 1810 , e 1 = 1042 К; Q = 247 , 1 Дж/г, a ₀ = 0,8 % .

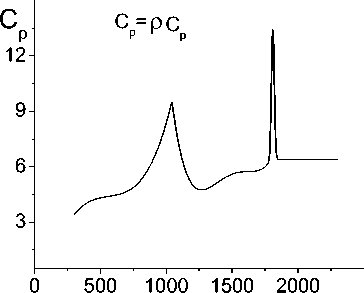
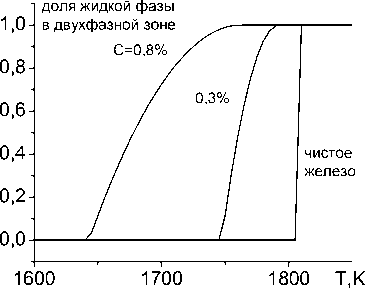
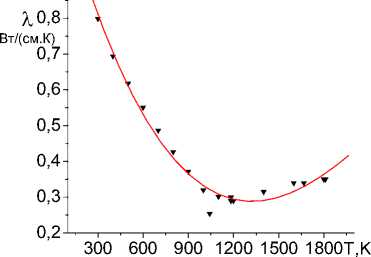
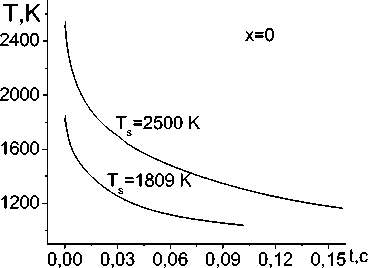
В некоторых случаях вместо (20) – (22) удобнее использовать аппроксимацию данных эксперимента [34,35] по теплоемкости чистого железа в виде c = -0,422 + 0,005 • T - 8,651-10-6 • T2 + 5,159-10-9 T3, T

c = 115,636 - 0,312 - T + 3,158-10 ^-4- T²-1,409-10^-7- T³+ 2,342-10^-11- T⁴, T >e1.

Зависимость теплоемкости от температуры без учета процессов в двухфазной зоне (включая окрестность точки плавления железа), основанная на аппроксимации экспериментальных данных и использовании 5 -образной функции в окрестности точки плавления, показана на рис. 10.

Рис. 10. Зависимость теплоемкости от температуры

Рис. 11. Доля жидкой фазы в двухфазной зоне в зависимости от температуры

Расчеты показали, что в области фазового перехода (плавления) теплоемкость в приближении двухфазной зоны меняется слабо. Зависимость доли жидкой фазы от температуры представлена на рис. 11

Экспериментальные данные по теплопроводности сталей с содержанием углерода до 0,8 % (рис. 12) можно описать единой зависимостью [31] (Вт/см²)

Х = 1,222 - 0,0016 • T - 8,3617•Ю^-7T²-1,1399 •Ю^-10T³.

Величина коэффициента диффузии углерода, естественно зависит от температуры и концентрации. В расчетах использованы следующие зависимости

D = ПDl +(1 -n)Ds ,     (25)

где

Ds =‘

' D_а,     T<91;

_DY, 91 < T< Tliq.

Рис. 12. Теплопроводность чистого железа

Коэффициенты диффузии в твердых фазах зависят от температуры по закону Аррениуса

D_а = 0,02 • exp(- 84219/ RT),

D_Y =[0,04 + 0,08a]• exp(-131356/RT) см²/с. (19)

Коэффициент диффузии углерода в жидком железе D_L , входящий в (25), в общем случае не описывается аррениусовской зависимостью. В [36] наиболее надежной считают зависимость вида

Dl =(0,84 + 0,26 • a)-10^-4см²/с,

справедливую для содержания углерода до 2,4 %.

Начальное распределение температуры аппроксимировано функцией вида f⁽x, y) = Tmax^exp^(- «• x²)• ^exP^(- Y • y).

Приведем лишь некоторые результаты исследования модели.

Очевидно, что температура наплавленной области постепенно уменьшается (рис. 13, нижняя кривая) вследствие прогрева подложки по механизму теплопроводности.

Распределение концентрации углерода имеет аналогичный вид, но глубина его проникновения незначительна (составляет несколько микрон). Это проиллюстрировано на рис. 14, где представлено распределение концентрации вдоль оси симметрии.

Рис. 13. Зависимость температуры поверхности от времени

Рис. 14. Распределение концентрации углерода в поверхностном слое t=1–0,00025; 2–0,0015; 3–0,00525; 4–0,07525; 5–5,0 с

Вследствие уменьшения температуры к моменту времени 0,007 с диффузия существенно замедляется и в дальнейшем происходит весьма слабое изменение размеров диффузионной зоны за время остывания подложки.

Интересно отметить, что вследствие зависимости температур ликвидуса и солидуса от концентрации углерода кристаллизация раньше начинается с поверхности, чему способствует теплоотдача, хотя и в меньшей степени.

Увеличение температуры расплавленной области в начальный момент времени приводит к более значительному прогреву подложки (верхняя кривая на рис. 14), более широкой диффузионной зоне, следствием чего, очевидно, будет более плавное изменение свойств в окрестности границы раздела материалов в результате обработки.

Вообще говоря, для описания процессов поверхностной обработки существует целый ряд более простых моделей, включающих в себя много качественных эффектов. В общем случае диффузионные явления, реализующиеся в технологических процессах в неравновесных условиях, следует изучать с учетом разнообразных перекрестных явлений.

Механические напряжения в зоне обработки

Вопрос об оценке механических напряжений в зоне обработки является весьма актуальным. Известные в механике подходы к оценке остаточных напряжений, вообще говоря, не дают представления о том, с какими необратимыми процессами они связаны. На практике же важно знать, как изменяются напряжения в зоне обработки при изменении технологических параметров, состава обрабатываемых слоев и сопутствующих физико-химических превращений. В этом случае плодотворным оказывается путь, основанный на термодинамике необратимых процессов, вернее, ее обобщении на деформируемые среды с химическими превращениями и диффузией. Подробно обобщение модели механики с использованием идей термодинамики описано, например, в [37, 38]. Здесь ограничимся простым примером.

Механическое поведение плоского образца (с покрытием или без него), который подвергается обработке источником энергии, движущимся вдоль поверхности в направлении одной из осей, можно описать в рамках представления об обобщенном плоском напряженном состоянии [39, 40].

Тогда для пластины, изображенной на рис. 3, при условии, что ширина сканирования равна ширине образца, имеют место соотношения:

G zz = G zx = G zy = 0 , CT XX =G XX (x, y ) , G yy =G yy (x, y ) .

Учитывая, что скорость распространения тепла при теплопроводности и скорость движения источника по поверхности много меньше скорости распространения механических возмущений, для оценки компонент тензора напряжений в первом приближении можем использовать идеи, описанные в [40] для задач термоупругости. Тогда для того, чтобы найти с_xx и сyy, нам потребуется решить задачу о равновесии при заданном распределении температуры T(x, t). Поскольку поле температуры при условии h_x = H_x не зависит от координаты y, можно предположить, что от координаты y не зависят и компоненты тензоров напряжений и деформаций.

Тогда для решения задачи о равновесии можно воспользоваться условиями совместности и условиями равенства нулю суммарных сил и суммарных моментов по контуру пластины. В чистом виде этот путь приемлем, когда не достигается температура плавления.

Именно такой способ оценки напряжений в диффузионной зоне использован в [41,42].

Более строгая постановка задачи для условий, проиллюстрированных на рис. 3, может быть сформулирована в рамках теории термоупругости для пластин с учетом возникающих прогибов и моментов. Но это выходит за рамки настоящей работы.

Заключение

Заметим, что все описанные в статье модели исследованы численно. Методы численного решения имеют свои особенности, описать которые в рамках этой статьи не представляется возможным Основная проблема – в разномасштабности физических процессов, учитываемых в моделях. Так, коэффициенты диффузии и температуропроводности для твердых сред отличаются на несколько порядков. Это приводит к тому, что характерные размеры зоны прогрева и диффузионной зоны существенно различны, особенно если принять во внимание аррениусовскую зависимость коэффициента диффузии от температуры. На порядки могут отличаться и парциальные коэффициенты диффузии в многокомпонентных системах. В свою очередь, области влияния чисто температурных напряжений и напряжений, возникающих в диффузионной зоне, также различны. Все это приводит к необходимости разработки специальных численных алгоритмов. Вариант алгоритма для неизотермических задач диффузии предложен, например, в [43]. Другая трудность в численном исследовании связана с тем, что в случае воздействия концентрированных источников энергии области, занимаемые разными фазами и обладающие различными теплофизическими и реологическими свойствами, существенно различаются по размерам. Основные физико-химические изменения происходят в области, много меньшей размеров всего образца. Это опять приводит к поиску специальных методов решения, что представляет собой отдельную нетривиальную задачу.