Моделирование фокусировки фемтосекундного импульса эллипсоидом, параболоидом, сферой и полусферой

В настоящее время лазеры ультракоротких импульсов получили огромное развитие. Разработаны и продемонстрированы методы генерации импульсов с длительностью менее 5 фс [1, 2]. Максимальная мощность фемтосекундных импульсов на данный момент может превышать 1 ПВт, а интенсивность при фокусировке пучка достигает 1021 Вт/см2 [3]. Уникальные характеристики ультракоротких импульсов обуславливают их широкое применение в фундаментальной науке, технике и медицине. Огромные интенсивности в сфокусированных пучках и связанные с нею напряжённости электрических и магнитных полей дают возможность изучать процессы взаимодействия света с веществом в режимах, прежде недоступных экспериментаторам. В химии и фотобиологии удаётся проследить ход самых быстрых химических реакций. Фемтосекундные импульсы нашли широкое применение в волоконной оптике [4] и в фемтосекундной и электронной микроскопии [5,6]. Высокая концентрация энергии при фокусировании пучков фемтосекундных лазеров открывает новый путь в прецизионной микрообработке материалов [7, 8], а в медицине обеспечивает возможность проведения тонких операций в офтальмологии и нейрохирургии [9].

Ввиду широкого применения ультракоротких импульсов в различных областях науки и техники множество работ посвящено способам их пространственно-временного преобразования и фокусировке [10, 11]. При моделировании процесса распространения ультракоротких импульсов необходимо использовать методы, учитывающие не только пространственную, но и частотную дисперсию материала [12 – 15]. Однако во многих случаях этими требованиями пренебрегают, так как применение таких методов значительно усложняет процедуру расчёта и увеличивает время работы программы.

Данная работа посвящена моделированию фокусировки фемтосекундного оптического импульса микролинзами с различными поверхностями второго порядка (сфера, полусфера, эллипсоид и параболоид).

Для учёта зависимости диэлектрической проницаемости от частоты излучения применялась модель Селлмейера. Было рассчитано среднеквадратическое отклонение результатов моделирования с помощью метода, не учитывающего зависимость диэлектрической проницаемости от частоты, от результатов, учитывающих такую зависимость. Расчёты проводились FDTD-методом, реализованным в программе FullWAVE.

1.    Параметры моделирования

Рассмотрим несколько фокусирующих микролинз, поверхности которых описываются вращением кривых второго порядка. Будем предполагать, что все линзы изготовлены из кварцевого стекла с показателем преломления n ₁ = 1,5.

На рис. 1 и 2 показаны сфера и полусфера, описываемые уравнением сферы с радиусом r = 1 мкм:

x ² + у ² + z ² = r 2 ,                                    (1)

где x , y , z – пространственные переменные.

В оптике известно свойство параболоида вращения собирать пучок лучей, параллельный главной оси в точку фокуса [16]. На этом свойстве основаны параболические антенны, телескопы-рефлекторы, прожекторы, автомобильные фары [17].

На рис. 3 представлена микролинза, поверхность которой описывается уравнением эллиптического параболоида вращения:

x ² y ²

”⁺< = z , a ² b ²

где a=b= 2,1 - коэффициенты парабол, а x е [-1,1] и у е[-1,1], чтобы образовывать на плоской грани круг радиуса r=1 мкм.

Известно также, что эллиптические микролинзы способны фокусировать излучение в одном из своих фокусов [16]. Используя формулы Френеля и правила геометрической оптики, можно рассчитать параметры эллипсоидальной линзы, которая будет фокусировать на плоскую грань параллельный пучок лу- чей, распространяющихся параллельно оптической оси (оси вращения эллипсоида).

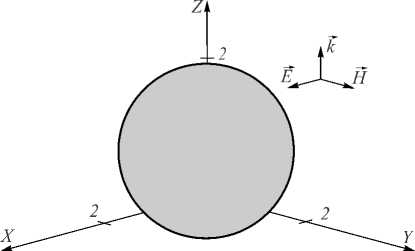
Рис. 1. Микросфера с радиусом 1 мкм

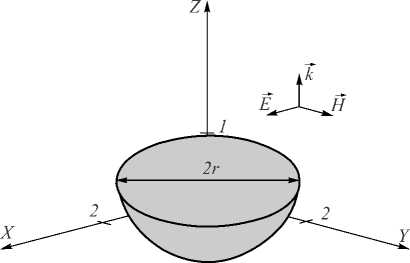
Рис. 2. Полусфера с радиусом 1 мкм

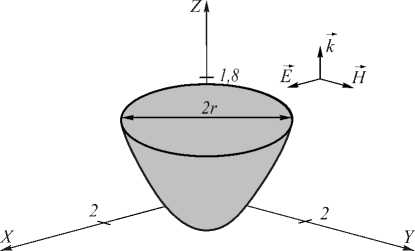
Рис. 3. Микропараболоид с радиусом 1 мкм

Поверхность данной микролинзы будет задаваться уравнением эллипсоида:

22 x 2    y

+ d2 e2

⁺ T ⁼1,

где d ² = e ²

22                        2

C A ₂ C A        n ₂

1 A , f = /        \2 , A = I I , С

1 - A (1 - A)2 l П )

свободная константа, n 1 – показатель преломления материала элемента, n 2 – показатель преломления среды. Выберем параметры линзы так, чтобы сечение на выходе было кругом с радиусом r = 1 мкм. Пусть средой является воздух ( n ₂ = 1), а линза изготовлена из кварцевого стекла ( n 1 = 1,5), как упоминалось ранее, тогда d ² = e ² = 1, f ² = 1,8. На рис. 4 представлена рассчитанная линза.

Для учёта зависимости диэлектрической проницаемости от частоты излучения воспользуемся моделью Селлмейера [18]:

e ⁽ % ) ^ ■ £— m ^X

^^^^^^e

A m X ²

^ m + i X8 Sm ’

где ε ∞ – диэлектрическая проницаемость на высоких частотах; λ – длина волны, мкм; λ m – резонансная длина волны, мкм; A m – величина резонанса; δ Sm – коэффициент демпфирования, мкм. Параметры модели для кварцевого стекла представлены в Таблице 1[18].

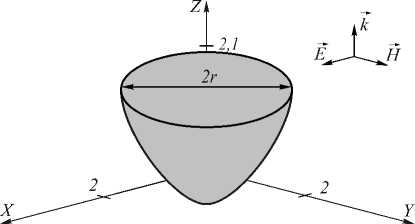
Рис. 4. Микроэллипсоид с радиусом 1 мкм

Таблица 1. Параметры модели Селлмейера для кварцевого стекла

m	A m	λ m	δ Sm
1	0,69616630	0,068404300	0
2	0,40794260	0,11624140	0
3	0,89747940	9,8961610	0
ε∞ = 1

Для моделирования без учёта дисперсии использовалось значение ε = 2,25, соответствующее общепринятому значению коэффициента преломления кварцевого стекла ( n ₁ = 1,5).

На выпуклую поверхность линзы падает короткий модулированный гауссов импульс с плоским фронтом и равномерной интенсивностью вида:

X

X exp ^-

t- 0,5 • c • t_s ?

td

I 2n ] sin| —T |, l X )

где a = P = 1,6 мкм - размер стороны квадрата, ограничивающего плоскую волну в начальной плоскости; τ = сt , мкм; с – скорость света, мкм/с; t – время, с; t s – длительность импульса, с; t d – ширина импульса, мкм. Длина волны импульса равна 0,532 мкм. Плоскость поляризации импульса совпадает с плоскостью XZ (отлична от нуля только компонента E x ).

Далее с помощью FDTD-метода моделируется прохождение через различные микролинзы двух фемтосекундных импульсов (5) длительностью 1,24 и 2,98 фс, а также постоянного излучения (CW). Моделирование производилось при следующих расстояниях между узлами сетки отсчётов: h x = 0,02 мкм, h y = 0,02 мкм, h z = 0,02 мкм, h τ = 0,01 мкм. На рис. 5 показано распределение интенсивности вдоль оптической оси входящих импульсов в свободном пространстве (до линзы). На рис. 6 показано временное распределение интенсивности входящих импульсов и соответствующие им спектры.

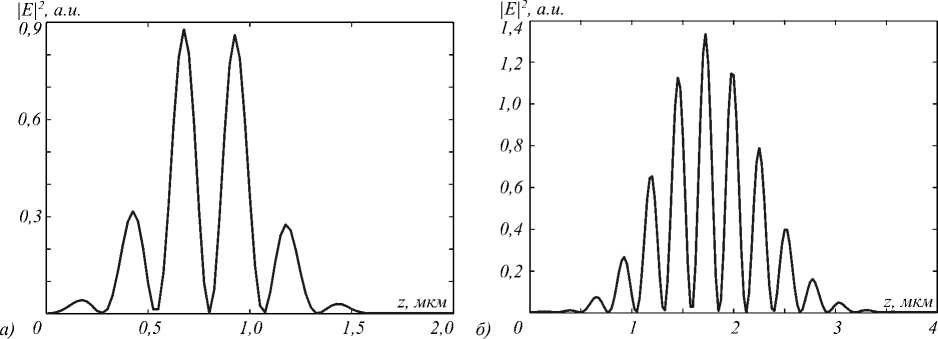
Рис.5. Распределение интенсивности (в произвольных единицах) вдоль оси z для входящего импульса длительностью: а) 1,24 фс; б) 2,98 фс

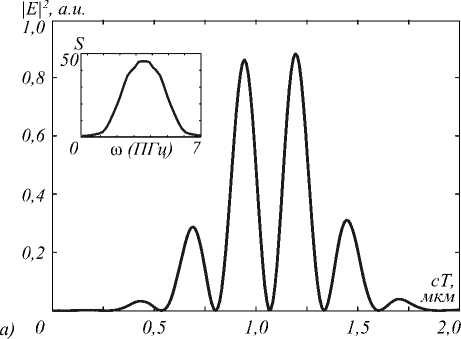
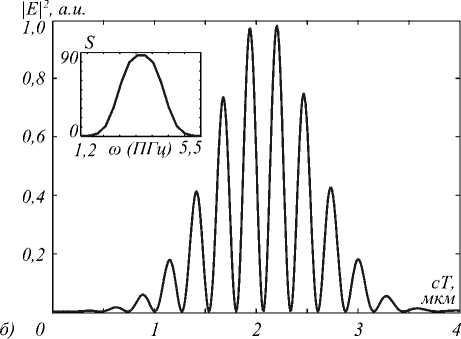
Рис.6. Временное распределение интенсивности в точке (0, 0, 0,2) и спектр для входящего импульса длительностью: 1,24 фс (а); 2,98 фс (б)

2.    Результаты моделирования

В ходе моделирования были рассчитаны расстояния, на которых происходила фокусировка импульсов (точка максимальной интенсивности). В Таблице 2 представлены соответствующие расстояния от выходной плоскости (для сферы – от точки на оптической оси) элемента до точки фокусировки.

Таблица 2. Расстояние от выходной плоскости микролинзы до плоскости фокусировки

	z f , мкм (1,24 фс)	z f , мкм (2,98 фс)	z f , мкм ( CW )
Сфера
£ = const	0	0	0
£(%)	0	0	–
Полусф		ера
£ = const	0,8	0,8	0,85
£(%)	0,8	0,8	–
Параболоид
£ = const	0	0	0,05
£(%)	0,1	0,1	–
Эллипсоид
£ = const	0,1	0,1	0,1
£(%)	0,1	0,1	–

На рис. 7 представлены распределения интенсивности импульса в момент фокусировки для каждой из вышеописанных микролинз. Выходные плоскости микролинз обозначены вертикальной линией.

В Таблицах 3–5 приведены размеры фокусного пятна по полуспаду интенсивности FHWM и глубина фокуса по полуспаду интенсивности DOF.

Из Таблиц 3–5 видно, что минимальное значение диаметра фокусного пятна по полуспаду интенсивности равно (0,42 ± 0,04) % (для любого излучения, сфокусированного сферой), а максимальная глубина фокуса (1,08 ± 0,04) % (для CW-волны, сфокусированной полусферой).

Рассчитаем коэффициент фокусировки по следующей формуле:

I kf = , (6)

Iin где kf – коэффициент фокусировки; If – величина максимальной интенсивности сфокусированного излучения, a.u. – произвольные единицы; Iin – величина максимальной интенсивности падающего излучения, a.u.

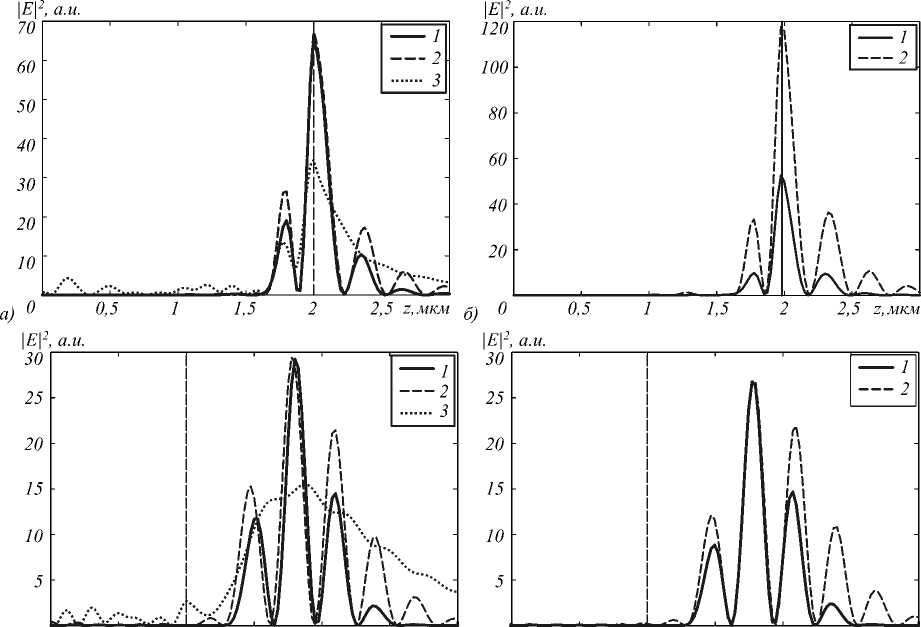
в) 0       0,5       1      1,5      2     2,5 г.мкм г) 0       0,5       1      1,5      2     2,5 z.mkm

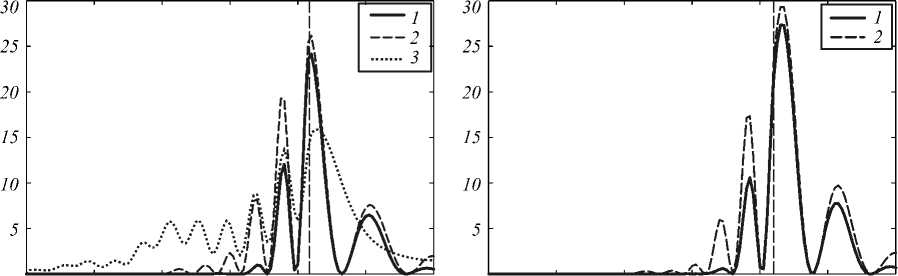
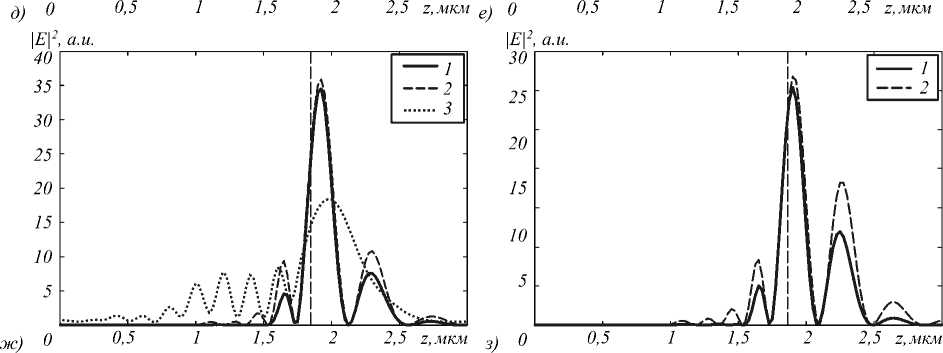
Рис. 7. Распределение интенсивности вдоль оптической оси для импульсов длительностью 1,24 фс (линия 1) и 2,98 фс (линия 2) и непрерывной волны (линия 3) в момент фокусировки: сфера ( е = const) (а); сфера ( е(Х) (б); полусфера ( е = const) (в); полусфера ( е(Х) (г); параболоид ( е = const) (д); параболоид ( е(Х) (е); эллипсоид ( е = const) (ж); эллипсоид ( е(Х) ) (з)

Таблица 3. Диаметр фокусного пятна по полуспаду интенсивности FHWM вдоль x (вдоль линии начальной поляризации)

	d x , λ (1,24 фс)	d x , λ (2,98 фс)	d x , λ (CW)
Сфера
£ = const	0,52	0,52	0,71
£(%)	0,61	0,52	-
Полусфера
£ = const	0,7	0,7	0,61
£(%)	0,7	0,7	-
Параболоид
£ = const	0,61	0,61	0,61
£(%)	0,52	0,61	-
Эллипсоид
£ = const	0,61	0,61	0,89
£(%)	0,61	0,61	-

Таблица 4. Диаметр фокусного пятна по полуспаду интенсивности FHWM вдоль y, которая перпендикулярна начальной плоскости поляризации

	d y , λ (1,24 фс)	d y , λ (2,98 фс)	d y , λ (CW)
Сфера
£ = const	0,42	0,4	0,42
£(%)	0,42	0,42	-
Полусфера
£ = const	0,61	0,7	0,71
£(%)	0,7	0,7	-
Параболоид
£ = const	0,42	0,42	0,42
£(%)	0,42	0,52	-
Эллипсоид
£ = const	0,52	0,52	0,52
£(%)	0,52	0,52	-

Таблица 5. Глубина фокуса по полуспаду интенсивности DOF вдоль z

	d z , λ (1,24 фс)	d z , λ (2,98 фс)	d z , λ (CW)
Сфера
£ = const	0,1	0,1	0,2
£(%)	0,15	0,18	-
Полусфера
£ = const	0,13	0,43	1,08
£(%)	0,35	0,65	-
Параболоид
£ = const	0,08	0,08	0,3
£(%)	0,15	0,15	-
Эллипсоид
£ = const	0,18	0,18	0,43
£(%)	0,15	0,48	-

Рассчитаем коэффициент пространственного уширения по следующей формуле:

k = dout e in

где k e – коэффициент пространственного уширения; d_in – длина входящего импульса по полуспаду интенсивности, мкм; d_out – длина выходящего импульса по полуспаду интенсивности, мкм.

Рассчитаем коэффициент временного уширения по следующей формуле:

kt = —, (8) tin где kt – коэффициент временного уширения; tin – длительность входящего импульса по полуспаду интенсивности, фс; tout – длительность выходящего импульса по полуспаду интенсивности, фс.

В Таблицах 6–8 приведены коэффициенты фокусировки пространственного и временного уширения.

Из Таблиц 6–8 видно, что максимальное значение коэффициента фокусировки равно 86,76 (для импульса длительностью 2,98 фс, сфокусированного сферой), хотя в остальных случаях более короткий импульс фокусируется лучше более длинного. Минимальные значения коэффициента пространственного и временного уширения равны соответственно 1,03 (для импульса длительностью 2,98 фс, сфокусированного эллипсоидом) и 1 (для любого импульса, сфокусированного сферой).

Таблица 8. Коэффициент временного уширения

1	k e (1,24 фс)	k e (2,98 фс)
Сфера
£ = const	1,46	1,24

Таблица 6. Коэффициент фокусировки

	k f (1,24 фс)	k f (2,98 фс)	k f (CW)
Сфера
£ = const	74,70	50,6	18,14
£(%)	56,63	86,76	-
Полусфера
£ = const	33,36	21,64	7,7
£(%)	30,07	20,12	-
Параболоид
£ = const	27,62	19,66	8,02
£(%)	28,23	20,25	-
Эллипсоид
£ = const	38,78	26,32	9, 33
£(%)	34,75	23,86	-

Таблица 7. Коэффициент пространственного уширения

	k e ( 1,24 фс)	k e (2,98 фс)
Сфера
£ = const	1,64	2,4
£(X)	1,71	1,97
Полусфера
£ = const	2,71	1,31
£(X)	2,79	1,34
Параболоид
£ = const	1,86	1,29
£(X)	1,86	1,29
Эллипсоид
£ = const	1,71	1,06
£(%)	1,64	1,03

E(X)	1	1
Полусфера
£ = const	1,49	1,24
£(%)	1,49	1,24
Параболоид
£ = const	1,51	1,25
£(%)	1,51	1,25
Эллипсоид
£ = const	1,49	1,24
£(%)	1,51	1,24

Рассчитаем коэффициент сужения спектра по следующей формуле:

k ™

^A® in

A® out ’

где k _ω – коэффициент сужения спектра; Δω _in – ширина спектра входящего излучения, ПГц; Δω _out – ширина спектра выходящего излучения, ПГц.

Таблица 9. Коэффициент сужения спектра

	k ω (1,24 фс)	k ω (2,98 фс)
Сфера
£ = const	1,56	1,42
£(%)	1,66	1,18
Полусфера
£ = const	1,18	1,07
£(%)	1,19	1,13
Параболоид
£ = const	1,13	1,05
£(%)	1,12	1,05
Эллипсоид
£ = const	1,74	1,6
£(%)	2,02	1,02

Из Таблиц 8 и 9 видно, что из-за продольной дифракции в пространстве все импульсы при распространении уширяются и, соответственно, их спектр сужается. При этом чем короче входящий импульс (а соответственно, шире спектр), тем больше коэффициент сужения.

Также были проведены исследования среднеквадратического (СКО) и максимального отклонений решений, полученных с учётом и без учёта зависимости диэлектрической проницаемости от частоты. Сравнение решений производилось в области фокусного пятна на момент фокусировки. Таким образом, СКО характеризует отклонение полученных решений в целом, в то время как максимальное отклонение может быть полезно для учёта пределов прочности оптических элементов для острой фокусировки излучения на элемент. В Таблице 9 приведены значения СКО отклонения η s и погрешности в равномерной норме η u .

Из Таблицы 10 видно, что СКО результатов моделирования с учётом и без учёта частотной дисперсии составляет от 3% до 30%. При этом стоит отметить, что погрешность в равномерной норме может дости- гать 46%. Максимальная СКО наблюдается при фокусировке сферой более длительного импульса. Причём чем короче входящий импульс, тем выше среднеквадратическое отклонение результатов моделирования (исключение составляют результаты, полученные для сферы). Это можно объяснить тем, что чем короче импульс, тем шире его спектр (Таблица 10), а значит, зависимость диэлектрической проницаемости сильнее влияет на результат. На рис. 8 представлена зависимость диэлектрической проницаемости от длины волны (вертикальные линии ограничивают область рабочих длин волн), а в Таблице 11 – границы спектра.

Таблица 10. Погрешности, возникающие при расчёте сфокусированных импульсов, если не учитывать частотную дисперсию элементов микрооптики

	η s , %	η u , %
Сфера
1,24 фс	15,57	32,33
2,98 фс	28,79	45,62
Полусфера
1,24 фс	4,41	7,7
2,98 фс	4,08	8,35
Параболоид
1,24 фс	2,66	4,38
2,98 фс	2,68	5, 36
Эллипсоид
1,24 фс	5	14
2,98 фс	4,6	14,59

Таблица 11. Границы спектра используемых импульсов

Длительность импульса	λ 1 , мкм	λ 2 , мкм
1,24 фс	0,374	0,833
2,98 фс	0,441	0,617

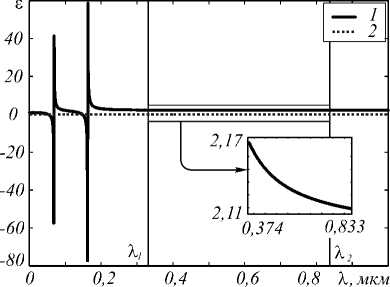
Рис. 8. Зависимость действительной (1) и мнимой (2) компонент диэлектрической проницаемости от длины волны

Заключение

В работе проведено моделирование FDTD-методом фокусировки двух фемтосекундных лазерных импульсов разной длительности с помощью четырёх микролинз (сфера, полусфера, параболоид, эллипсоид) с эквивалентными параметрами и с учётом частотной дисперсии вещества.

Получены следующие результаты.

• 1)    Ширина фокусного пятна по полуспаду интенсивности в плоскости, перпендикулярной плоскости поляризации, не зависит от длительности импульса и от дисперсии вещества. Сфера и параболоид формируют одинаковые и меньшие фокусные пятна ((0,42 ± 0,04)λ), чем эллипсоид ((0,52 ± 0,04)λ) и полусфера ((0,70 ± 0,04)λ).

• 2)    Ширина фокусного пятна по полуспаду интенсивности в плоскости, параллельной плоскости поляризации, также не зависит от длительности импульса и дисперсии вещества. Сфера формирует меньшее фокусное пятно ((0,52 ± 0,04)λ), чем параболоид ((0,61 ± 0,04)λ), и эллипсоид ((0,61 ± 0,04)λ), и полусфера ((0,70 ± 0,04)λ). Заметим, что полусфера с числовой апертурой NA =0,7 формирует круглое фокусное пятно с диаметром (0,70 ± 0,04)λ, что согласуется с дифракционным пределом 0,51λ/ NA =0,71λ.

• 3)    Глубина фокуса для полусферы и эллипсоида пропорционально зависит от длительности импульса и почти не зависит от длительности импульса для сферы и параболоида.

• 4)    Интенсивность в фокусе (и отношение интенсивности в фокусе к интенсивности падающего света) больше для более короткого импульса при фокусировке полусферой, параболоидом и эллипсоидом. И наоборот, при фокусировке микросферой интенсивность в фокусе больше для более длительного импульса.

• 5)    Пространственное и временное уширение импульса на выходе из оптического элемента к импульсу на входе оказывается больше для более короткого импульса при фокусировке полусферой, параболоидом и эллипсоидом. И наоборот, при фокусировке сферой пространственное уширение больше для менее короткого импульса, а временного уширения для обоих импульсов нет.

• 6)    Несмотря на слабую зависимость дисперсионной кривой для кварца от длины волны в области видимого спектра (рис. 9), результаты фокусировки коротких импульсов микросферой могут приводить к относительной ошибке в 15–28 %, если не учитывать частотную дисперсию вещества. А при расчёте фокусировки фемтосекундных импульсов с длиной волны 532 нм с помощью кварцевых полусферы (NA=0,7), параболоида или эллипсоида зависимостью дисперсии вещества от частоты можно пренебречь, так как её неучёт приводит к ошибке в 3–5%.

Работа выполнена при поддержке гранта Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и грантов РФФИ (12-07-00269, 13-0797008).