Моделирование фокусировки линейно-поляризованного света с помощью субволнового бинарного аксикона

Фокусировка света в ближней зоне с помощью элементов микрооптики с субволновыми неоднородностями интенсивно изучается, так как субволновое фокусное пятно может использоваться в нанолитографии, микроскопии ближнего поля и оптической микроманипуляции. Фокусное пятно, сформированное вблизи поверхности раздела сред, имеет несколько преимуществ перед острой фокусировкой в дальней зоне (в фокусе высокоапертурного объектива). Во-первых, из-за наличия в ближней зоне затухающих поверхностных волн можно сформировать фокусное пятно много меньше длины волны. Во-вторых, это фокусное пятно будет меньше в n раз (n – показатель преломления фокусирующего элемента), чем фокусное пятно в дальней зоне. В-третьих, интенсивность в фокусе будет в n2 раз больше, чем интенсивность в вакууме. И, в-четвёртых, в ближней зоне субволнового оптического элемента будут присутствовать, кроме затухающих волн, и распространяющиеся волны (нулевой порядок дифракции), которые могут достичь наблюдателя в дальней зоне. В [1,2] описаны реальные отражательные сканирующие микроскопы ближнего поля, в которых используются оптические элементы, фокусирующие вблизи своей поверхности. Примеров недавних работ, в которых изучается субволновая фокусировка лазерного света, множество. Например, в [3] экспериментально изучается фокусировка света с помощью кольцевой структуры (3 кольца с числовой апертурой NA = 0,91), выполненной в плёнке золота, толщиной 100 нм, напылённой на торец одномодового волокна диаметром 2 мкм (длина волны 808 нм). Эта структура формировала на расстоянии 1,2 мкм эллиптическое фокусное пятно с диаметрами по главным осям эллипса 0,42λ и 0,52λ. Заметим, что эффективность такой фокусировки низкая (5%). В [4] численно показано, что специально подобранные 9 нанощелей в плёнке золота действуют как цилиндрическая линза и формируют на расстоянии 0,5λ поперечный фокусный отрезок шириной FWHM = 0,22λ (λ = 633 нм). В [5] с помощью 2 сквозных и 2 несквозных нанощелей в плёнке серебра толщиной 200 нм также сформирован поперечный фокусный отрезок длиной около 1 мкм и шириной FWHM = 0,29λ (расчёт) и FWHM = 0,34λ (эксперимент) на расстоянии 0,3λ от плёнки.

Экспериментально бинарный микроаксикон исследовался в [6] с помощью микроскопа ближнего поля. Было показано, что на расстоянии 1 мкм от аксикона, освещённого линейно-поляризованным лазерным светом, формировалось почти круглое фокусное пятно с диаметром FWHM=0,58λ. Если учесть, что числовая апертура этого аксикона была равна NA =0,67 (период – 800 нм, длина волны – 532 нм), то диаметр этого пучка (FWHM = 0,39λ / NA ) будет меньше дифракционного предела (FWHM=0,51λ / NA ). В [7] моделировались бинарные аксикон и биаксикон (аксикон со сбоем фазы по диаметру) с NA = 1 (период T равен λ = 10,6 мкм). Было показано, что вблизи биаксикона при линейной поляризации формируется круглое пятно с диаметром FWHM=0,32λ и площадью HMA=0,08λ². С учётом показателя преломления материала биаксикона ( n =2,4) диаметр и площадь пятна будут иметь следующие значения: FWHM=0,76λ /n и HMA=0,46λ²/ n ². Данный результат получен для дальнего ИК-диапазона, который используется обычно в лазерных технологиях, а получить его для видимого диапазона не удалось. Так, в [8] моделирование бинарного биаксикона с NA от 0,97 до 1,01 (рис. 3 б и табл. 1) показало, что на расстояниях, равных 0,6λ и λ (λ =532 нм), не возникает круглого фокусного пятна и диаметр вдоль поляризации равен FWHM=0,34λ (боковые лепестки составляют 75%). В [8] также экспериментально исследовались бинарные аксикон и биак-сикон с T =500 нм ( NA = 1,06). Для аксикона были получены эллиптические световые пятна на расстоянии 100 нм (FWHM 0,40λ × 0,54λ) и 650 нм (FWHM 0,48λ × 0,52λ). С учётом числовой апертуры эти фокусные пятна больше, чем полученные в [6] (FWHM = 0,39λ / NA ). Кроме того, в [8] так и не удалось получить круглое световое пятно с помощью биакси-кона (получено пятно в виде участка дуги).

В данной работе методом разностного решения уравнений Максвелла (FDTD-методом) показано, что при освещении линейно-поляризованным гауссовым лазерным пучком (λ =532 нм) стеклянного бинарного аксикона с периодом 0,98λ в непосредственной близи от поверхности аксикона на оптической оси формируется эллиптическое фокусное пятно. Диаметры фокусного пятна по полуспаду интенсивности (FWHM) по главным осям равны 0,26λ и 0,61λ. Площадь фокусного пятна по полуспаду интенсивности (HMA) равна 0,125λ2, что меньше, чем можно получить в фокусе зонной пластинки [9] или в фокусе параболического зеркала [10] для радиально-поляризованного света и с приемлемым уровнем боковых лепестков. Глубина фокуса по полуспаду интенсивности (DOF) равна 0,4λ, максимальная интенсивность в фокусе в 45 раз больше, чем максимальная интенсивность падающего света, а боковые лепестки составляют 30% от максимального значения интенсивности. Это минимальное фокусное пятно, которое можно сформировать с помощью бинарного аксикона с таким уровнем боковых лепестков. Если для данного случая рассчитать не интенсивность, а поток энергии (модуль проекции на оптическую ось вектора Умова–Пойнтинга), то вместо эллиптического фокусного пятна будет круглое с диаметром немного большим, чем минимальный диаметр эллиптического пятна.

Результаты моделирования

Моделировалось прохождение линейно-поляризованного гауссова пучка с длиной волны λ = 532 нм и радиусом ω =7λ через бинарный микро-аксикон с радиусом R = 8 мкм, показателем преломления материала n = 1,52 и высотой рельефа h =532 нм. Подложка считалась бесконечной, и поэтому не учитывалось френелевское отражение (около 4%) от её гладкой поверхности (этой поверхности просто нет в расчётной схеме). Источник излучения (перетяжка гауссова пучка) находился на расстоянии 0,5 мкм от ближайшей точки рельефа поверхности аксикона.

Моделирование проводилось BOR–FDTD методом [11], шаг сетки по пространству – λ /50, по времени – λ /100c, где с – скорость света в вакууме. Рассматривались аксиконы с периодами от T =500 нм до T =700 нм. При T > λ фокусное пятно (максимальная интенсивность на оптической оси) формируется на некотором расстоянии от ступенчатой поверхности акси-кона. Например, при T =700 нм – на расстоянии f =3λ, при T =650 нм – на расстоянии f =2,5λ. При дальнейшем уменьшении периода аксикона T фокус приближается к поверхности и при T = λ достигает ступенчатой поверхности аксикона (поверхности центрального цилиндрического выступа аксикона диаметром T). При дальнейшем уменьшении периода аксикона максимум интенсивности на оптической оси возникает внутри бинарного аксикона, а за поверхностью аксикона в свободном пространстве осевая интенсивность монотонно спадает. Это согласуется со скалярной теорией, в которой бинарный аксикон рассматривается как кольцевая дифракционная решётка, числовая апертура которой рассчитывается по формуле решётки NA=sin θ = λ /T. Из этой формулы следует, что при T < λ угол дифракции θ будет больше 90 градусов, то есть фокус на оптической оси будет формироваться внутри аксикона. При этом (T < λ) в приложениях можно использовать осевую интенсивность сразу за поверхностью аксикона, так как вблизи поверхности интенсивность достигает относительно большой величины по сравнению с интенсивностью падающего излучения. Например, интенсивность в фокусе при T =700 нм равна 15 относительным единицам, а интенсивность вблизи поверхности аксикона при T =510 нм равна 60 относительным единицам, то есть в 60 раз больше, чем интенсивность падающего света. Недостатком фокусного пятна для аксикона с периодом T =510 нм является то, что боковые лепестки достигают 50% от максимального значения интенсивности и не позволяют использовать фокусное пятно в приложениях. Из всех рассмотренных примеров оптимальными параметрами обладало фокусное пятно для ак-сикона с периодом T =520 нм. На рис. 1а показано осевое распределение интенсивности для бинарного акси-кона с периодом T =520 нм. На рис. 1б показан его увеличенный фрагмент. Заштрихованная область на рис. 1б соответствует области внутри аксикона. Видно, что максимум интенсивности на оси находится внутри аксикона, а за аксиконом интенсивность спадает монотонно и имеет глубину фокуса по полуспаду интенсивности (считая от поверхности аксикона) DOF=0,4λ.

На рис. 2 показаны поперечные сечения интенсивности «фокуса» в свободном пространстве в непосредственной близости от поверхности аксикона. На рис. 2 а показано центральное сечение по оси, перпендикулярной плоскости поляризации падающего света, а на рис. 2 б – центральное сечение интенсивности в фокусе по оси, параллельной плоскости поляризации света. Видно, что в фокусе сформировался эллипс, меньший диаметр которого по полуспаду интенсивности равен FWHM=0,26λ, а больший диаметр равен FWHM=0,61λ. Эти значения рассчитаны с точностью ±0,01λ. Боковые лепестки картины дифракции на рис. 2 а составляют 30% от максимального значения интенсивности. Максимальная интенсивность в фокусе в 45 раз превышает интенсивность падающего света. Это наименьшее фокусное пятно, которое можно получить для линейно-поляризованного света с помощью стеклянного бинарного микроаксикона с боковыми лепестками меньшими 50%. У аксиконов с периодом 510 нм и 500 нм фокусные пятна меньше, чем у аксикона с периодом 520 нм (табл. 1), но боковые лепестки вокруг центрального фокуса превышают 50%.

Фокусное пятно на рис. 2 имеет эллиптическую форму, и его площадь по полуспаду интенсивности равна HMA=0,125λ². Значение HMA вычислялось как площадь эллипса ( πab/4 ) с диаметрами по главным осям ( a и b ), взятыми из двух последних столбцов табл. 1. Это значение (HMA=0,125λ²) меньше, чем площадь минимального круглого пятна, предсказанного теоретически для зонной пластинки (HMA=0,154λ²) в [9] и экспериментально полученного с помощью параболического зеркала (HMA=0,134λ²) в [10] при фокусировке радиально-поляризованного лазерного света.

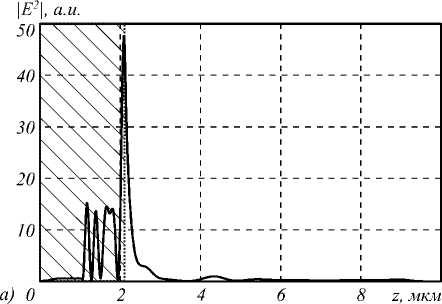
Рис. 1. Распределение интенсивности вдоль оптической оси аксикона с периодом T = 520 нм (а), увеличенный фрагмент этой кривой (заштрихованная область соответствует области внутри аксикона) (б)

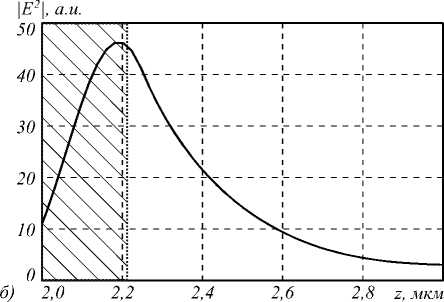
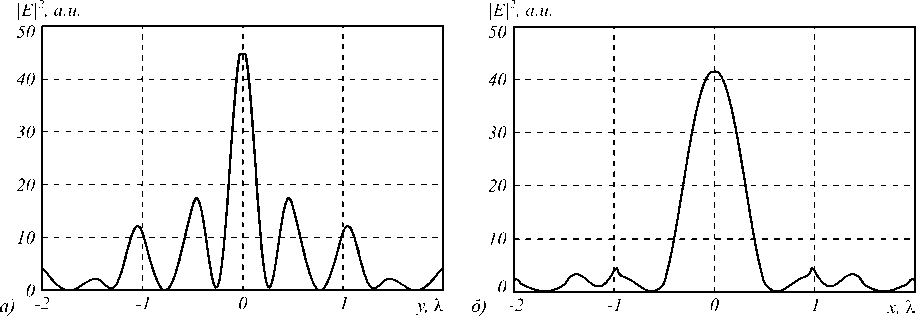
Рис. 2. Распределение интенсивности в плоскости (а) перпендикулярной и (б) параллельной к направлению поляризации непосредственно за границей рельефа аксикона

Таблица 1. Значения диаметров фокусного пятна по полуспаду интенсивности FWHM, рассчитанных для аксиконов с разными периодами T для длины волны λ = 532 нм

Период аксикона T, нм	Интенсивность на оси z в плоскости фокуса, a.u.	Диаметры фокусного пятна
		вдоль оси y , перпендикулярной плоскости поляризации FWHM y , λ	вдоль оси x , параллельной плоскости поляризации FWHM x , λ
700	15	0,48	0,73
600	20	0,39	0,79
590	17	0,37	0,81
580	18	0,36	0,85
570	21	0,35	0,86
560	21	0,35	0,85
550	15	0,36	0,87
540*	7	0,32	0,82
532*	30	0,28	0,73
530*	25	0,29	0,75
520*	45	0,26	0,61
510*	60	0,26	0,52
500*	35	0,24	0,56

* – фокус рассчитан непосредственно за границей рельефа аксикона, т.к. максимальное значение интенсивности находится внутри аксикона.

Из табл. 1, в частности, видно, что с ростом периода аксикона (и ростом расстояния, на котором формируется фокус) степень эллиптичности фокусного пятна уменьшается. Так, при T =700 нм отношение главных осей фокусного пятна равно 0,66, а при T =530 нм это отношение равно 0,39.

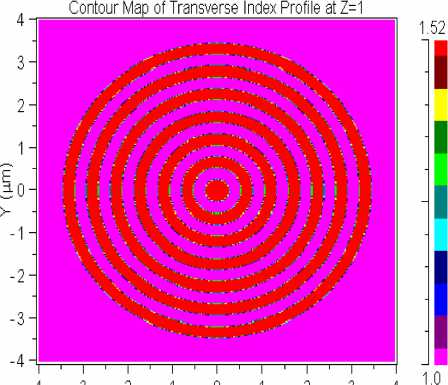
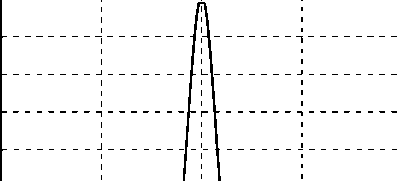
Для проверки правильности предыдущих расчётов было проведено сравнение результатов фокусировки линейно-поляризованного гауссова пучка бинарным аксиконом (рис. 3), полученных с помощью разных программ. На рис. 4 приведены сечения интенсивности фокусного пятна поперёк плоскости поляризации для аксикона с периодом T = λ (рис. 3), рассчитанные с помощью BOR-FDTD метода (рис. 4 а ) и FDTD метода в декартовых координатах, реализованного с помощью программы FullWAVE (рис. 4 б ). У обоих сечений фокусного пятна на рис. 4 диаметр по полуспаду интенсивности равен FWHM y = 0,28λ. Заметим, что на рис. 4 а и 4 б разные нормировки, поэтому и разные числовые значения интенсивности.

Параметры моделирования в FullWAVE: шаг сетки по пространству – 0,028 мкм = λ /19, по времени – 0,011 мкм/ c = λ /48 c , где c – скорость света в вакууме. Плоскость поляризации совпадает с плоскостью XZ .

■                X(nm)                "

Рис. 3. Расположение бинарного микроаксикона с периодом T = λ в расчётном поле (кольца имеют показатель преломления 1,52, а фон имеет показатель преломления 1)

\E\2, a.u.

а) -2           -1           0           1 y,X

\E\2, a.u.

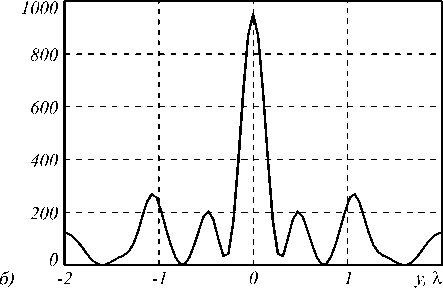
Рис. 4. Распределение интенсивности в плоскости, перпендикулярной к направлению поляризации, непосредственно за границей рельефа аксикона с периодом T = 532 нм, рассчитанное с помощью

BOR-FDTD метода (а) и с помощью FullWAVE (б)

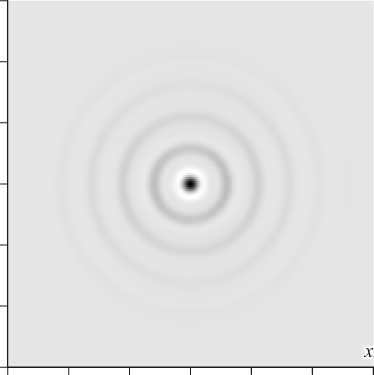
Интересно заметить, что при расчёте не интенсивности (плотность световой энергии), а потока световой энергии (модуль проекции на оптическую ось вектора Умова–Пойнтинга) вместо эллиптического фокусного пятна возникает круглое пятно с диаметром немного большим, чем меньший диаметр эллиптического фокусного пятна интенсивности. На рис. 5а показана двумерная картина интенсивности (в полутонах серого, рассчитанная с помощью FullWAVE) вблизи бинарного аксикона с периодом T = λ (рис. 3), а на рис. 5б показана картина потока световой энергии в той же плоскости.

y/X A

0 -■■

-2

• -4-

• x/X

• -6 -|-----------1-----------1-----------1-----------1-----------11—>^

• а)    -6     -4     -2      0      2      46

y!X^x

6 T

-2

-4

• б)    -6      -4      -2      0      2       4       6

Рис. 5. Распределение интенсивности (плотности энергии) (а) и потока энергии (модуля проекции на оптическую ось вектора Умова–Пойнтинга) (б) вблизи поверхности (на расстоянии λ/20) бинарного микроаксикона с периодом T = λ

Из рис. 5 видно, что поток энергии формирует круглый фокус с диаметром по полуспаду равным FWHM=0,36λ, в то время как интенсивность формирует эллиптический фокус с диаметрами по декартовым осям FWHM x =0,75λ и FWHM y =0,30λ. Это объясняется тем, что продольная составляющая электрического поля не даёт вклада в продольную составляющую вектора Умова–Пойнтинга. Продольная составляющая вектора электрического поля возникает в плоскости поляризации XZ при схождении лучей в фокус. В перпендикулярной плоскости YZ при схождении лучей в фокус продольная составляющая вектора электрического поля не возникает.

|£|J, а. и.

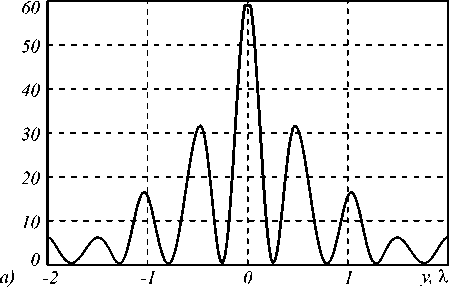
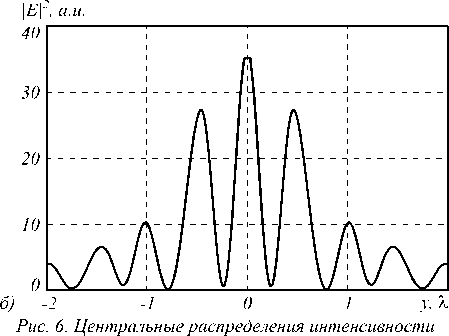
вдоль оси, перпендикулярной плоскости поляризации, рассчитанные сразу за поверхностью аксиконов с периодами T = 510 нм (а) и Т = 500 нм (б)

На рис. 6 показаны центральные сечения интенсивности вдоль оси Y , перпендикулярной плоскости поляризации, рассчитанные вблизи поверхности бинарных аксиконов с периодами меньшими, чем у ак-сикона на рис. 3: T =510 нм (рис. 6 а ) и Т =500 нм (рис. 6 б ).

Полная ширина по полуспаду интенсивности центрального лепестка в обоих случаях равна, соответственно, FWHM _y = 0,26λ и FWHM _y = 0,24λ. Хотя площади этих двух эллиптических фокусных пятен почти равны HMA=0,106λ² и меньше, чем у фокусного пятна на рис. 2 HMA=0,125λ² , уровень боковых лепестков у них неприемлемо высокий: 50% (рис. 6 а ) и 70% (рис. 6 б ).

Интересно заметить, что субволновый аксикон формирует фокусное пятно, по параметрам сравнимое с характеристиками интерференционной картины, формируемой волноводной дифракционной решёткой с затухающими порядками [12]. В [12] период картины меньше длины волны в 3-4 раза (на рис. 6 а FWHM _y = λ /3,8), интенсивность в максимуме в 100 раз больше интенсивности падающего света (на рис. 6 а интенсивность в 60 раз больше), максимальный контраст интерференционной картины равен 0,6 (на рис. 6 а интенсивность спадает до нуля – контраст единичный).

Заключение

В работе получен следующий результат. Методом разностного решения уравнений Максвелла показано, что при освещении линейно-поляризованным гауссовым лазерным пучком стеклянного бинарного аксикона с субволновым периодом (период равен 0,98 длины волны) в непосредственной близи от поверхности аксикона на оптической оси формируется в поперечном сечении эллиптическое фокусное пятно с размерами по полуспаду интенсивности по декартовым осям 0,26λ и 0,61λ (площадь пятна 0,125λ2, λ – длина волны); глубина фокуса 0,4λ; максимальная интенсивность в фокусе в 45 раз превосходит максимальную интенсивность падающего света; боковые лепестки, окружающие фокус, составляют 30% от его максимального значения. Площадь этого пятна меньше, чем в [9, 10]. Это минимальное фокусное пятно, которое можно сформировать с помощью бинарного аксикона с таким уровнем боковых лепестков . Если для данного случая рассчитать не интенсивность, а поток энергии (модуль проекции на оптическую ось вектора Умова–Пойнтинга), то вместо эллиптического фокусного пятна будет круглое фокусное пятно с диаметром немного большим, чем минимальный диаметр эллиптического пятна.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и молодого кандидата наук (МК-3912.2012.2) и гранта РФФИ (12-07-00269).