Моделирование фокусировки жесткого рентгеновского излучения последовательностью цилиндрических отверстий в алмазной плёнке

В сентябре 2017 вступил в строй новый Европейский рентгеновский лазер на свободных электронах (XFEL, Гамбург), который генерирует рентгеновское электромагнитное излучение высокой интенсивности, мощность которого (1020 Вт/см2 для рентгена с энергией 9,9 кэВ) превышает мощность рентгеновского излучения, получаемого на синхротронах [1]. Поэтому интерес к использованию компонент рентгеновской оптики в таких мегаустановках в последнее время возрос [2, 3]. В [2] с помощью 20 последовательных микролинз в бериллии сфокусировали рентгеновское излучение (8,2 кэВ) на расстоянии 250 мм в фокусное пятно с диаметром FWHM = 150 нм (число Штраля – 0,8). В [3] когерентное рентгеновское излучение (10 кэВ) с помощью двух эллиптических отражающих зеркал, работающих на полном внешнем отражении, было с эффективностью 100% сфокусировано на расстоянии 1,5 м в пятно с размерами 0,95×1,20 мкм.

Одним из перспективных материалов для создания рефракционных и дифракционных компонент рентгеновской оптики является алмаз. У него самое большое отличие показателя преломления от единицы: δ = n – 1 = 7,3×10^-6 (для жесткого рентгена 10 кэВ). Эта величина для алюминия равна 5,46×10^-6 и для кремния 4,84×10^-6. Это напрямую связано с высокой плотностью алмаза 3,52 г/см³. Алмаз слабо поглощает жесткое рентгеновское излучение. Если кварц толщиной 2 мм поглощает 95 % рентгеновского излучения (15 кэВ), то алмаз – только 41 %. Кроме того, алмаз обладает рекордно высокой теплопроводностью 20–22 Вт/см ⋅ K, что делает его исключительно перспективным материалом для транспортировки мощных рентгеновских пучков, например, от источников синхротронного излучения.

Поэтому компоненты рентгеновской оптики на алмазе привлекают большое внимание исследователей. В [4] фемтосекундный импульс рентгеновского лазера (8 кэВ) с помощью зонной пластинки, изготовленной из алмазной мембраны, диаметром 500 мкм с крайней зоной 100 нм и глубиной рельефа 2,1 мкм, с эффективностью 2 % сфокусировали в пятно диаметром FWHM = 320 нм. Зонная пластинка хотя и формирует наноразмерное фокусное пятно, но обладает низкой дифракционной эффективностью (несколько процентов). Повысить эффективность зонных пластинок можно с использованием участков рельефа, работающих в высших порядках дифракции [5]. Но еще более эффективно использовать одну или несколько последовательных рефракционных микролинз. Можно также использовать эффект полного внешнего отражения. Например, в [6] экспериментально показано, что кристаллический алмаз может отражать 100 % (полное внешнее отражение) жесткого рентгеновского излучения (от 10 кэВ до 25 кэВ) [6]. Современный обзор по рентгеновской кристаллической алмазной оптике можно найти в [7]. Но при отражении жесткого рентгеновского излучения высокие требования предъявляются к минимизации уровня шероховатости поверхности (даже при скользящем падении). При фокусировке рентгеновского излучения на пропускание требования к шероховатости существенно меньшие. Так, шероховатость поверхности линзы в несколько нанометров, хотя и гораздо больше длины волны жесткого рентгеновского излучения (0,15 нм), но в задержку излучения по фазе дает несущественный вклад из-за малой величины разности в показателе преломления алмаза и вакуума δ = n – 1 = 7,3×10-6. Поэтому рефракционные микролинзы в кристаллическом алмазе и поликристаллических пленках активно исследуются. В [8] исследуется рефракционная параболическая микролинза в кристаллическом алмазе: радиус у вершины параболы – 100 мкм, перетяжка (самое узкое место линзы) – 50 мкм, шероховатость – 1 мкм, фокусное расстояние – 13,3 м, и размеры фокусного пятна для длины волны 13,6 кэВ равны FWHMx = 183 мкм и FWHMy = 86 мкм. В [9] те же ав- торы провели численное сравнительное исследование рентгеновской микролинзы из алмаза и бериллия и выяснили, что алмазная линза имеет в 8–10 раз меньший температурный коэффициент расширения. В [10] на подложке с рельефом из кремния по технологии CVD (chemiсal vapor deposition) были сформированы последовательно расположенные микроотверстия (параболические микролинзы) с апертурой 300 мкм и радиусом при вершине параболы 60 мкм. Толщина алмазной пленки была равна 40 мкм. Набор таких микролинз для рентгена с квантами энергии в 12 кэВ имел фокусное расстояние 560 см и формировал фокус в виде отрезка с меньшей стороной, равной по полуспаду интенсивности FWHM = 1,6 мкм. В [11] с помощью абляции материала фемтосекундным импульсом в слое поликристаллического алмаза (толщина 600 мкм), полученного по технологии CVD, были сформированы последовательно расположенные планарные микролинзы (6 линз) диаметром больше 200 мкм, с помощью которых рентгеновское излучение (11 кэВ) на расстоянии 1,42 м было сфокусировано в отрезок с меньшей шириной FWHM=2,8 мкм. Причем интенсивность в фокусе в 40 превышала входную интенсивность.

Из этого краткого обзора видно, что с помощью набора планарных микролинз (микроотверстий в алмазной пленке или слое), полученных по технологии литографии [10] или абляции [11], получаются сходные результаты фокусировки: FWHM = 1,6 мкм [10] и FWHM=2,8 мкм [11]. Хотя размеры фокуса, полученные с помощью 20 последовательных линз в пленке бериллия, были на порядок меньше: FWHM = 150 нм [2]. Возникает вопрос: как от числа микроотверстий в пленке и от их размеров зависят расстояние до фокуса и его размеры?

В данной работе с помощью программы BeamProp (фирмы RSoft) и программы расчета интеграла Рэлея– Зоммерфельда моделируется фокусировка жесткого рентгеновского излучения (9,25 кэВ) через последовательность круглых микроотверстий в алмазной пленке. Получены зависимости фокусного расстояния, эффективности фокусировки, размеров фокусного пятна и максимальной интенсивности в фокусе от числа микроотверстий. Показано, что с помощью всего 20 отверстий можно сфокусировать рентгеновское излучение с длиной волны 1,34 А на расстоянии 1,5 см от отверстий в отрезок шириной 200 нм. Этот результат согласуется в результатом работы [2]. Для существенного ускорения расчетов был применен простой, но эффективный метод: так как все линзы одинаковые, то прохождение излучения через последующие линзы заменяется умножением на известную функцию.

Прохождение рентгеновского излучения через круглое цилиндрическое отверстие

Рентгеновское излучение с длиной волны λ = 1,34 A (9,25 кэВ) проходит в алмазной пленке толщиной 2 мкм, в которой выполнено одно отверстие с диаметром D = 10 мкм, и показателем преломления внутри n = 1.

Показатель преломления алмаза для рентгеновского излучения выберем в виде [4] n =1–7,3×10^–6+3×10^-9 i . При выбранных показателе преломления и длине волны разность в набеге фазы в π между воздухом и материалом

можно получить при прохождении излучения через материал толщиной 9,17 мкм. Поэтому диаметр отверстия на рис. 1 выбран равным 10 мкм.

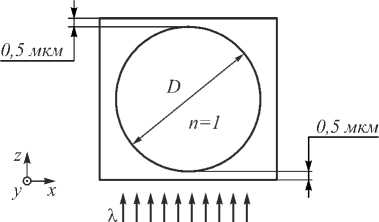
Рис. 1. Схема рассматриваемой задачи: круглое отверстие в алмазной плёнке диаметром D = 10 мкм

Расчет прохождения излучения через отверстие проводился с помощью BeamProp. В этом программном пакете используется параксиальное решение уравнения Гельмгольца для монохроматической волны:

д2ф д 2ф д2ф

2 + 2 + 2 + k ° n ( x , У , z ) Ф = °, д x д у д z

где к ° = 2 п / % - волновое число в вакууме, n ( x, у, z ) -комплексный показатель преломления, заданный на всей области расчета. Это уравнение не учитывает

переотражения излучения назад и резонансы в тонких пленках, однако в данной работе эти эффекты несущественны. Так как искомое поле можно разложить

на медленно меняющуюся комплексную амплитуду u ( x, y, z ), описывающую огибающую поля, и быструю

экспоненту:

ф ( x , у , z ) = u ( x , у , z ) e i ° ⁿ * z ,

где n * – базовый показатель преломления в однородной среде, характеризующий точность огибающей, то подставляя (2) в (1), получим следующее приближение:

д u д z

- i

2 k ₀ n _*

Гд ² u д ² u

( l x ? ⁺ly ? ⁺

( к °2 n ²

- к °2 n * ) u

Это основное уравнение, которое и решается в программном пакете BeamPROP с помощью разностной схемы Кранка–Николсона.

Время расчета составило приблизительно 2,5 часа. Параметры расчета: сетка вдоль осей X , Y , Z была соответственно λ, 200λ, 10λ (0,134 нм, 26,8 нм, 1,34 нм), выходное поле имело размеры 12,5×2,2 мкм (9702×83 пикселей).

После прохождения через цилиндр излучение распространялось в свободном пространстве. Распростра-

нение рентгеновского излучения в вакууме рассчитывалось с помощью интеграла Рэлея–Зоммерфельда (примерно 5 минут). Тот же результат можно получить с помощью преобразования Френеля, выбор Рэлея–Зом-мерфельда обусловлен наличием ПО для его расчета.

На рис. 2 по горизонтали отложены сантиметры, а по вертикали – интенсивность в произвольных единицах. Из рис. 2 видно, что имеют место несколько локальных максимумов интенсивности. Интенсивность в последнем максимуме (будем называть его фокусом) всего на 8,2 % превышает интенсивность падающего поля (прошедшего через цилиндр). Это объясняется большой расходимостью пучка вдоль оси Y из-за того, что алмазная плёнка имеет толщину 2 мкм.

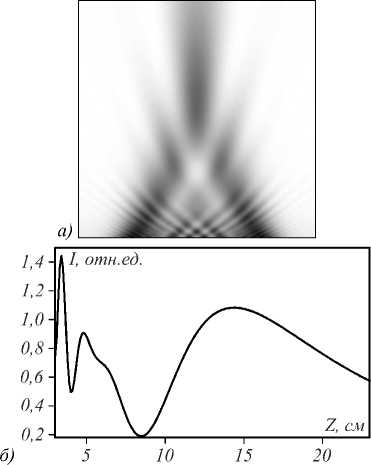
Рис. 2. Интенсивность излучения (негатив) в плоскости XZ (Y = 0) после прохождения через один цилиндр (рис. 1) и сечение вдоль продольной оси Z через центр пучка X = 0.

Поле получено в координатах X ∈ (–6 мкм; 6 мкм),

Z ∈ (3 см; 23 см). Последний максимум наблюдается на расстоянии Z = 14,4 см

Дифракционная эффективность фокусировки по уровню 1/2 составляет 33,7 %, а по уровню 1/10 – 60,1 %. Размеры фокусного пятна по полуспаду интенсивности на рис. 3 а равны FWHMy = 8,55 мкм и FWHMx=1,53 мкм.

Для увеличения эффективности фокусировки мы увеличили толщину алмазного волновода до 10 мкм, чтобы он был равен диаметру отверстия.

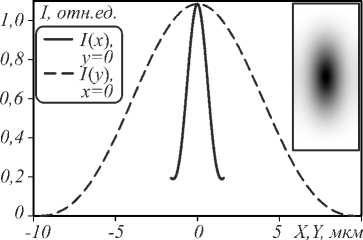
Рис. 3. Интенсивность излучения в фокусном пятне и его сечения по осям. Размер кадра – 2,84×18,7 мкм

На рис. 4 показан результат моделирования: по горизонтальной оси – сантиметры, по вертикальной – отношение интенсивностей на выходе и входе. Интенсивность в фокусе, который теперь наблюдается на расстоянии Z = 19,4835 см, в 8,52 раза превосходит интенсивность прошедшего отверстие пучка. Эффективность фокусировки по уровню 1/2 – 39,5 %, по уровню 1/10 – 86,5 %. И размеры фокусного пятна равны FWHMx = 6,29 мкм и FWHMy = 1,95 мкм.

4 г о б)

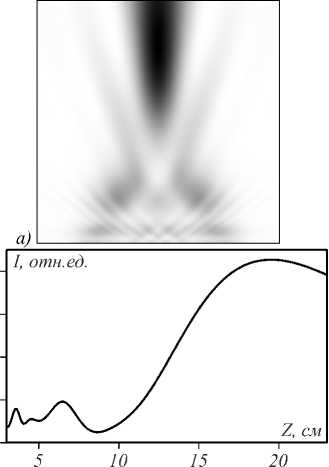
Рис. 4. Интенсивность излучения (негатив) в плоскости XZ (Y = 0) после прохождения через один цилиндр (рис. 1) с толщиной плёнки 10 мкм (а), сечение вдоль оси Z через центр пучка X = 0. Поле получено в координатах X∈(–6 мкм; 6 мкм), Z∈(3 см; 23 см)

Прохождение рентгеновского излучения через две цилиндрические линзы

Далее были рассмотрены две последовательные одинаковые линзы (рис. 5). Общая длина линзы составила 22 мкм, диаметр каждой линзы D = 10 мкм. Толщина алмазной пленки – 2 мкм. Прохождение рентгеновского излучения через обе линзы рассчитывалось с помощью программы BeamPROP (фирмы RSoft), время расчета – около 7 часов.

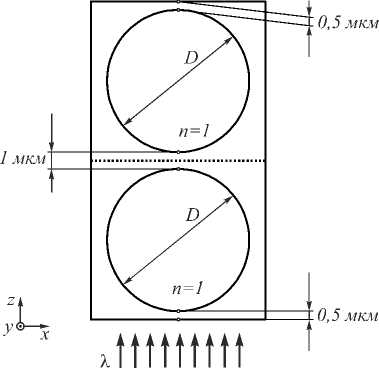
Рис. 5. Схема двух цилиндрических линз. Падающая волна плоская

На рис. 6 представлено распределение интенсивности рентгеновского излучения в плоскости XZ. Фо- кусное расстояние уменьшилось в 1,58 раза. Размеры фокусного пятна тоже уменьшились (так как увеличилась числовая апертура): FWHMx=5,48 мкм и FWHMy=0,945 мкм (рис. 7). Максимум интенсивности в фокусе в 2,695 раза превышает интенсивность на входе.

О

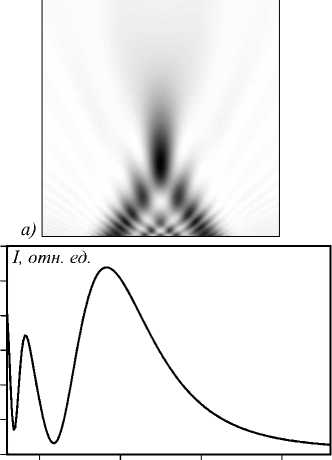
б)      5       10       15      20 Z.cm

Рис. 6. Распределение интенсивности после двух цилиндрических линз в плоскости XZ (Y = 0). Максимум наблюдается в точке Z = 91,306 мм

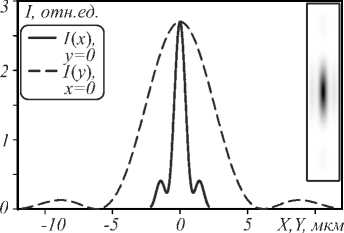
Рис. 7. Распределение интенсивности на расстоянии Z = 91,306 мм (в фокусе)

Усовершенствованный метод расчета

Так как оптическая система представляет собой последовательный набор одинаковых отверстий, то возникает желание заменить расчет прохождения излучения через последовательность линз на умножение (столько раз, сколько линз) поля, прошедшего первую линзу, самого на себя.

Эта идея была проверена на фокусировке рентгеновского излучения последовательностью из 10 отверстий. Рассчитывалось прохождение рентгеновского излучения через 10 линз, как на рис. 1 (время расчёта – примерно сутки), после чего с помощью интеграла Рэлея–Зоммерфельда считалось распределение интенсивности в фокусном пятне и вдоль оптической оси. Также рассчитывалось прохождение излучения через первую цилиндрическую линзу (3 часа), после чего прошедшее поле умножалось само на себя 9 раз

(несколько минут). Далее так же рассчитывалось поле на оси и в фокусной плоскости. Сравнение результатов расчета можно видеть на рис. 8.

Непрерывный график получен с помощью эконо- мичного по времени алгоритма умножения поля самого на себя, прерывистая линия – расчет в BeamPROP прохождения излучения через 10 линз. Из рис. 8 видно, что графики почти совпадают. Несовпадение графиков вызвано неточностью расположения двух начальных полей в 0,5 отсчета. Графики для поперечного распределения интенсивности (и размеры фокусных пятен) полностью совпадают (до 5 значащих цифр). Предложенный метод позволяет почти в 10 раз (если линз 10) уменьшить время расчета.

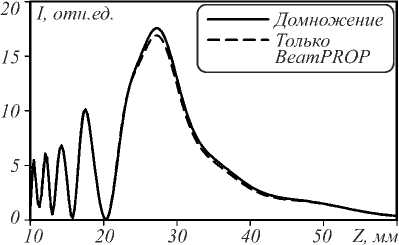
Рис. 8. Распределение интенсивности вдоль оптической оси для случая фокусировки рентгеновского излучения последовательностью из 10 круглых отверстий диаметром 10 мкм

Зависимость фокусного расстояния от количества линз

Предложенный метод позволил получить зависимости эффективности, фокусного расстояния, интенсивности в фокусе и размеров фокуса от числа линз в последовательности. Распределение интенсивности вдоль оптической оси в случае последовательности из 9 линз показано на рис. 9. Видно, что фокус в данном случае имеет увеличенную глубину (около 5 мм) и находится на расстоянии примерно 30 мм от последовательности линз. Отметим, что интенсивность в фокусе в 14 раз превышает входную интенсивность

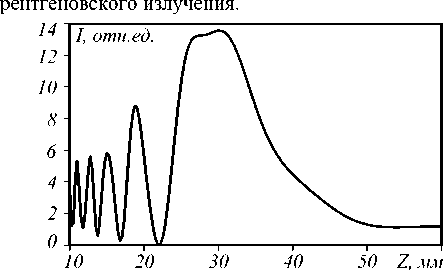
Рис. 9. Распределение интенсивности на оптической оси для случая фокусировки рентгеновского излучения 9 цилиндрическими линзами, стоящими подряд

На рис. 10 показаны результаты расчета для последовательности из нескольких линз с параметрами, как на рис. 1.

Из рис. 10 видно, что эффективность фокусировки даже при 20 последовательных отверстиях (длина последовательности из 20 линз 220 мкм) больше 35 %, а фокусное расстояние уменьшается в 10 раз по сравнению с 1 отверстием и равно 15 мм.

Эффективность Г], %      Фокусное расстояние / ж

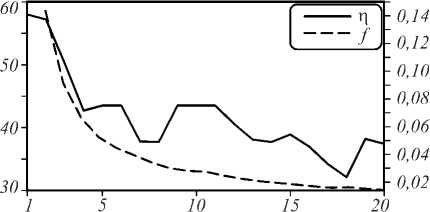
Количество линз N

Рис. 10. Зависимость эффективности фокусировки по уровню 0,1 от максимума интенсивности и ширины фокусного пятна по полуспаду интенсивности от количества последовательных отверстий

На рис. 11 показаны зависимости размера фокусного пятна вдоль поперечной оси X и относительной интенсивности в фокусе от числа последовательных отверстий. Из рис. 11 видно, что размер фокусного пятна уменьшается с 1,5 мкм до 200 нм (для 20 линз), а максимальная интенсивность в фокусе растет и для 20 отверстий в 45 раз превышает интенсивность на входе.

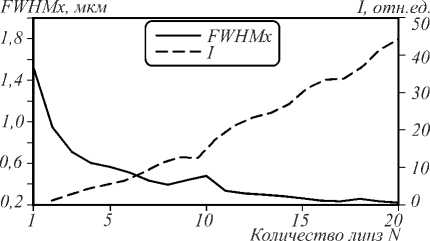
Рис. 11. Зависимость ширины по полуспаду интенсивности фокусного пятна вдоль оси X и относительной интенсивности в максимуме фокусного пятна от количества цилиндрических линз

Заключение

В работе получены следующие численные результаты. При строгом расчете прохождения жесткого рентгеновского излучения с длиной волны в несколько ангстрем через компоненты микрооптики с размерами в десятки и сотни микрон требуются трехмерные сетки из огромного числа отсчетов (1015). Это приводит к тому, что на современных персональных компьютерах одна задача решается несколько дней. Поэтому любые усовершенствования, приводящие к экономии времени, позволяют увеличить число решенных задач. Так как в данной работе рассматривается прохождение рентгеновского излучения через последовательность одинаковых микролинз, то оказалось, что, рассчитав точно прохождение излучения только через первую линзу, выходное поле можно далее умножать само на себя столько раз, сколько линз в последовательности. Это сокращает время расчета в число раз, равное числу линз в последовательности. Это было проверено численно (рис. 8). Такое усовершенствование позволило получить кривые изменения фокусного расстояния, размеров фокусного пятна, максимальной интенсивности в фокусе и дифракционной эффективности фокусировки. Было получено, что с помощью всего 20 отверстий можно сфокусировать рентгеновское излучение с длиной волны 1,34 А на расстоянии 1,5 см от отверстий в отрезок шириной 200 нм. Этот результат согласуется c результатом работы [2]. Чтобы уменьшить степень эллиптичности фокусного пятна, надо увеличить толщину пленки, чтобы размер отверстия был примерно равен толщине пленки. Например, при фокусировке одним отверстием с диаметром 10 мкм в алмазной пленке толщиной 2 мкм размеры фокуса равны 8,5×1,5 мкм, а при увеличении толщины пленки до 10 мкм вытянутость эллиптического фокуса уменьшается в 2 раза: размеры фокуса – 6,29×1,95 мкм.

Работа выполнена в рамках Программы повышения конкурентоспособности Самарского национального исследовательского университета имени академика С.П. Королева по проекту РНФ №14-22-00243.