Моделирование формирования ближнего порядка в процессе аморфного затвердевания металла

Потенциальная энергия системы определяется следующим выражением [2]:

Uij=∑Fi(ρi)+1∑Vij(rij),(2)

i2 где Vij (rij ) – парный межатомный потенциал (чаще всего просто отталкивающий), который является функцией расстояния rij между атомами i и j ; Fi - функция электронной плотности ρi , создаваемой в точке нахождения атома i всеми остальными атомами системы.

Электронная плотность около атома i определяется следующим образом:

ρi = ∑ρaj(rij), j≠i где ρaj(r) – электронная плотность атома j .

Уравнения движения решаются при периодических граничных условиях. Начальные координаты располагаются в узлах решетки. Значения v ^α _i ( t ₀ ) ≠ 0 задаются лишь для нескольких частиц, затем делается 10–100 шагов с большим τ . Обычно этого достаточно, чтобы все v_i ^α ( t ₀ + n τ ) , где n – число шагов, были не равны нулю. Координаты частиц x_i ^α ( t ₀ + n τ ) при этом также «перемешиваются», образуя почти случайное распределение [3].

Причиной затруднения перегруппировок атомов являются квантовые запреты, действие которых моделируется введением фиктивной поправки F ст к взаимодействиям [1]. Доля влияния каждого атома j на стабилизирующую поправку F ст ⁱ данного атома i убывает по мере роста расстояния r ij , пропорционально r ij^m , но не слишком быстро. Чтобы эффективно стабилизировать структуру, добавляемые силы должны быть достаточно дальнодействующими в том смысле, что интенсивность притяжения данного атома i к своему узлу должна определяться средним упорядочением, или уклонением δ _cp весьма большого числа окружающих атомов, чтобы поправки F ст и энергетические барьеры, препятствующие перегруппировки нескольких атомов, мало зависели от положения самих перегруппировывающихся атомов. В противном случае небольшие по энергии силы F ст легко преодолевались бы тепловыми флуктуациями в небольших объемах. Радиус дальнодействия сил F ст нужно принять примерно 1 микрон и больше. Отсюда m =4.

В [1] записан следующий гипотетический потенциал стабилизирующей поправки к обычным взаимодействиям:

2 πδ k sin

F ст =           ^d ,                                                      (3)

δ c ^- p ³(0,2 d -δ cp )

где Fст – величина силы притяжения рассматриваемого атома к «своему» узлу, d – период решетки, R - радиус дальнодействия силы Fст, 5 cp, 5i - среднее и индивидуальное отклонение частиц от «своих» узлов.

У 5,г,-3

ii

5 cp

' (суммирование в области r <  R ).

У у i

Доля а «вымороженных» атомов определяется следующей формулой а n

v

b

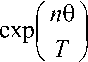
- ¹

где 0  - характеристическая температура, b - нормировочный множитель, определяемый из условия равенства 1 (или 100 %) суммы У аn долей всех уровней.

Для анализа структурных изменений будут проводиться исследование поведения парных радиальных функций распределения.

N ( r ) =

g (/ r _i

^- r j /) = g ( ^r ) =

V dN ( r )

N 4 n r ² dr

N

I — I yN (r)

V N 1^   I

– среднее число частиц, разделенное расстоянием r .

Результаты вычислений

Был рассмотрен процесс кристаллизации кластера Ni. Кластер выдерживался при температуре 1800 ºК (что выше его температуры плавления) длительное время – 200ps (1×10⁵ Δ t , где Δ t =2 fs представляло время 1 МД шага), с целью полного разрушения дальнего порядка. Далее в процессе моделирования температура системы ступенчато понижалась на 250 ºК. При каждой фиксированной температуре кластер выдерживался 0,4 ns (2×10⁵ Δ t ).

Для вычисления сил межатомного взаимодействия используется модель Клери и Розато [4]. В этой модели потенциальная энергия системы вычисляется по следующему выражению:

E = У i

^“

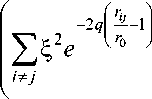
) ²

+ -

У Ae

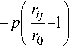
i * j

где А – энергия связи, константы p и q определяются по экспериментальным значениям периода решетки и упругих констант, ^ - кинетическая энергия электронов, перемещающихся в зоне проводимости.

Значения этих параметров для Ni:

А=0,1368 eV, ^ =1,756 eV, p=10, q=2,7, r0 =0,352 нм.

На основе полученных данных были построены функции радиального распределения для различных значений температуры.

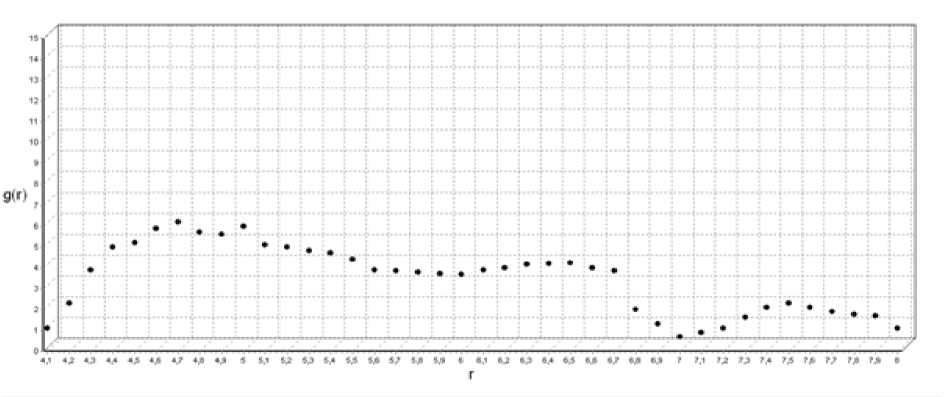
Рис. 1. Функция радиального распределения для T=1800 ºK

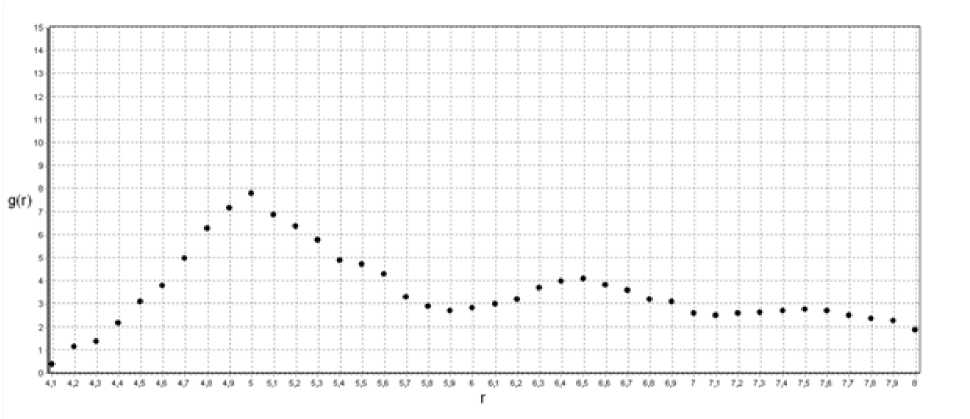
Рис.2. Функция радиального распределения для Т=1300 ºК

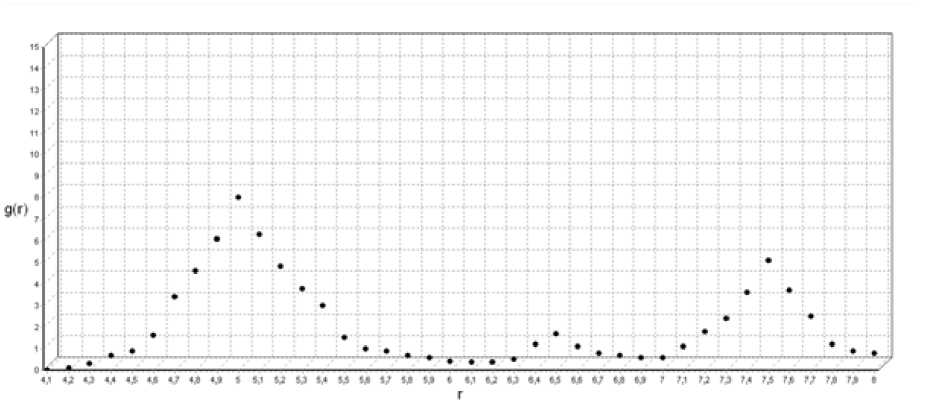
Рис. 3. Функция радиального распределения для Т=800 ºК

При температуре 1800 ºК (рис. 1) кластер находится в аморфном состоянии, так как у функции радиального распределения нет четко выраженных пиков, что свидетельствует об отсутствии дальнего порядка в расположении атомов.

При температуре 1300 ºК (рис. 2)кластер сильно флуктирует, но у функции радиального распределения появляется первый пик, что свидетельствует о начале процесса установления ближнего порядка в первой координационной сфере.

При температуре 800 ºК (рис. 3) первый пик функции радиального распределения увеличивается по высоте и сужается, что свидетельствует о том, что в первой координационной сфере появился объем, в котором наблюдается ближний порядок в расположении атомов. Второй ярко выраженный пик функции радиального распределения соответствует второй координационной сфере, в которой также появляется объем с повышенной упорядоченностью во взаимном расположении атомов.

Для аморфных структур в [5] предложено оценивать переход в твердое состояние по коэффициенту самодиффузии. Этот коэффициент определяется по тангенсу угла наклона кривой зависимости среднего квадрата смещения частиц от времени:

N 2

R^R 2 \ = i £k< t ) - x - (0)] . (7) \ i = 1

Таким образом, производная по времени от этой функции определяет коэффициент самодиффузии, температура, вблизи которой резко уменьшается коэффициент самодиффузии считается температурой перехода в аморфное состояние. В этом случае считается, что для частицы в твердом состоянии средний квадрат смещения вначале растет до определенного значения, равного амплитуде колебаний, и дальше со временем не меняется, а для диффундирующих частиц (в жидком состоянии) эта величина все время растет.

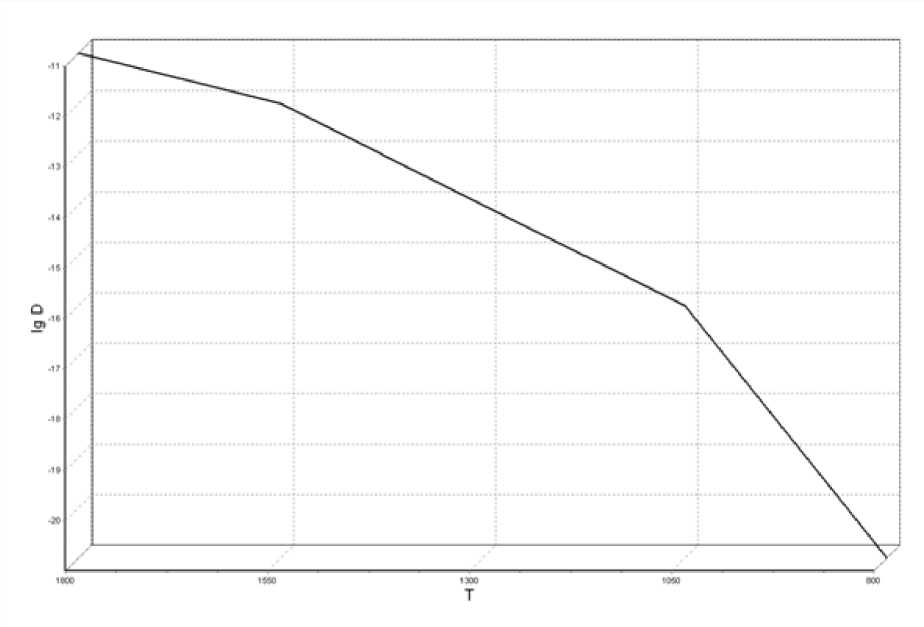
Рис. 4. Температурная зависимость коэффициента самодиффузии

На рис. 4 приведена температурная зависимость коэффициента самодифузии. При температуре 800 ºК коэффициент диффузии понижается на 5 порядков, температурная зависимость коэффициента диффузии претерпевает скачок, что свидетельствует об изменении фазового состояния системы.

В работе была рассмотрена задача описания процесса аморфного затвердевания с целью определения условий перехода между различными структурными состояниями. Приведена общая постановка задачи, рассмотрен процесс затвердевания кластера Ni. На основе полученных данных были построены функции радиального распределения. Как видно из анализа функций радиального распределения, в кластере существуют объемы с повышенной упорядоченностью во взаимном расположении атомов. Причем эти объемы оказываются относительно устойчивыми во времени. Также был вычислен коэффициент диффузии, с помощью которого можно обнаружить изменение фазового состояния системы.

Работа выполнена при поддержке гранта CRDF Y3–EP–09–09 Американского фонда гражданских исследований