Моделирование формирования изображения зонной пластинки в рентгеновском излучении

Использование мягкого и жёсткого рентгеновского излучения в оптических системах позволяет получать высокое разрешение в задачах микроскопии [1]. Короткая длина волны рентгеновского излучения по сравнению с видимым светом накладывает более жёсткие условия на расчёт и изготовление оптики – линз Френеля, зонных пластинок, дифракционных решёток [2-4].

Зонные пластинки (ЗП) являются одним из самых простых элементов для фокусирования когерентного рентгеновского излучения [4-7]. Теория их расчёта известна давно [8], однако интерес представляет также и моделирование распространения света через рассчитанную зонную пластинку. В [9] описываются результаты эксперимента с использованием составной ЗП, формирующей изображение в первом и третьем прошедших порядках. Однако в данных работах не проводилось численное моделирование прохождения излучения через ЗП. Основной проблемой для расчёта дифракции рентгеновского излучения на ЗП является вычислительная сложность задачи, обусловленная малой длиной волны излучения. Длина волны рентгеновского диапазона составляет обычно доли нанометра, поэтому необходимо использовать сетку отсчётов с разбиением в несколько тысяч или десятков тысяч отсчётов по линейным координатам, что требует значительных временных затрат для моделирования на компьютере.

В работе впервые приводятся результаты моделирования формирования изображения в когерентном и частично когерентном рентгеновском излучении, проведённого в Суперкомпьютерном центре «Сергей Королёв» (СГАУ). В рамках скалярной теории дифракции произведено компьютерное моделирование формирования изображения с помощью зонной пластинки в жёстком рентгеновском излучении. При этом параметры зонной пластинки, формирующей изображение в компьютерном эксперименте, соответствуют пара-

метрам реально созданной зонной пластинки. Это позволит в дальнейшем сравнить результаты компьютерного моделирования и физического эксперимента. Рассматриваемая оптическая схема в этой работе близка к реальной схеме будущего эксперимента. С целью уменьшения размеров оптической схемы в работе моделируется формирование несфокусированного изображения. Моделируется формирование изображения в частично-когерентном излучении, которое близко к излучению рентгеновских трубок. Для проверки правильности расчётов приводится сравнение численного моделирования получения увеличенного в 1160 раз изображения дифракционных решёток с периодом 50 и 100 нм с результатами эксперимента с аналогичными параметрами, описанного в [9].

Моделирование

Моделирование распространения излучения проводилось в электромагнитном приближении. Использование геометрооптического приближения (на-

пример, реализованного в коммерческом программном пакете TracePro) для моделирования формирования изображения невозможно, так как ЗП состоит

из плоско-параллельных участков, которые не изменяют ход лучей. А также при лучевом приближении не учитывается набег фазы на ступеньках ЗП и час-

тичная когерентность падающего пучка.

Выбор метода численного моделирования распространения рентгеновского излучения приведён в [10]. Из [10] следует, что для моделирования распространения излучения через ЗП целесообразно использовать программное обеспечение BeamProp (фирма-разработчик RSoft Design Group), для расчёта распространения излучения в свободном пространстве – интеграл Рэлея-Зоммерфельда. В BeamProp реализовано решение уравнения Гельмгольца (Beam Propagation Method) в приближении медленно меняющейся амплитуды поля:

d u d z

i 2 k ₀ n

| 3 2 u d ² u

( 3^2 + 3/+

( k 0 - k 02 n ² ) u

где k ₀ = 2 π/λ – волновое число, n – показатель преломления вещества, u – комплексная амплитуда рентгеновского излучения, ( x , y ) – поперечные координаты, z – продольная координата. Приближение медленно меняющейся амплитуды поля хорошо подходит для расчёта рентгеновских дифракционных элементов, поскольку действительная часть показателя преломления для рентгеновского излучения имеет порядок 1 - 10 ^{- 4}...1 - 10 ^{- 8} , а мнимая – 10 ^{- 5}...10 ^{- 8} [11].

Для построения изображения с помощью рентгеновского излучения с длиной волны λ = 0,229 нм была изготовлена ЗП радиусом 100 мкм с фокусным расстоянием 25 см, ширина крайних зон 286 нм [12]. Такое фокусное расстояние было выбрано, исходя из критерия возможности изготовления ЗП на литографическом оборудовании. ЗП была выполнена на мембране из нитрида кремния толщиной 200 нм в слое серебра толщиной 900 нм, глубина рельефа была ограничена производственными возможностями и составила 460 нм. Показатель преломления материала дифракционного рельефа зонной пластинки равен n = 1 - 6,8 ⋅ 10 ^{- 5} + 6,8 ⋅ 10 ^{- 6} i . Моделирование показало, что эффективность фокусировки излучения такой зонной пластинкой составляет 4,25% по полуспаду интенсивности в случае плоской падающей волны.

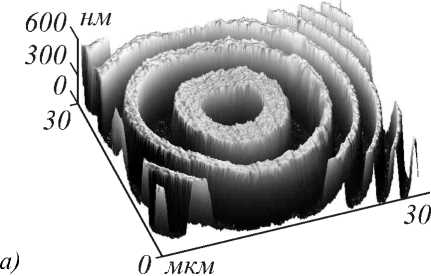
На рис. 1 представлен рельеф зонной пластинки, полученный сканирующим зондовым микроскопом Solver-Pro M (NT-MDT, Зеленоград).

Высота, нм 600 500

б)

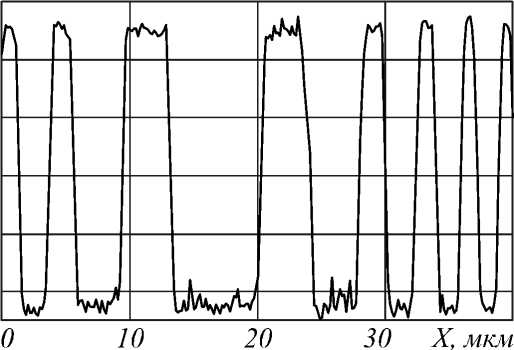
Рис. 1. Рельеф центральной части зонной пластинки [11]: восстановленное трехмёрное изображение (а), его профиль (б)

Расчёт распространения рентгеновского излучения через зонную пластинку производился комбинированным методом. Расчёт в свободном пространстве до ЗП производился с помощью интеграла Рэлея-Зоммерфельда в Суперкомпьютерном центре «Сергей Королёв» (использовалось 800 процессоров Intel Xeon 5593 2,93 ГГц).

Расчёт прохождения света через зонную пластинку производился программой BeamProp, и дальнейший расчёт прохождения излучения в свободном пространстве после ЗП производился тоже с помощью интеграла Рэлея-Зоммерфельда. Использовалась сетка 1547×1547 отсчётов (расстояние между отсчётами 0,13 мкм), всё поле имело размер 201×201 мкм. Заметим, что, хотя разбиение сетки отсчётов может показаться слишком грубым (567λ между отсчётами), это не влияет на правильность результатов, так как фаза в падающем поле не изменяется более чем на 2π между отсчётами.

На рис. 2 представлен профиль фазы комплексной амплитуды рентгеновского излучения в плоскости объекта-транспаранта. Видно, что фаза поля внутри изображаемого объекта хорошо прописывается.

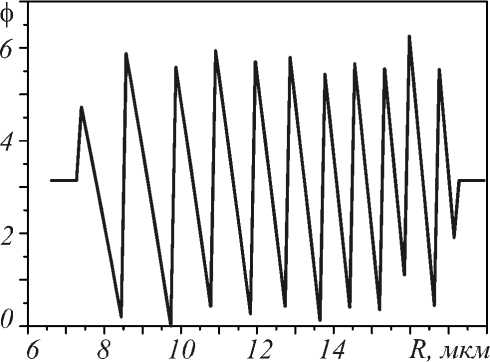
Рис. 2. Профиль фазы φ внутри изображаемого объекта

На рис. 3 представлена оптическая схема рассматриваемой задачи.

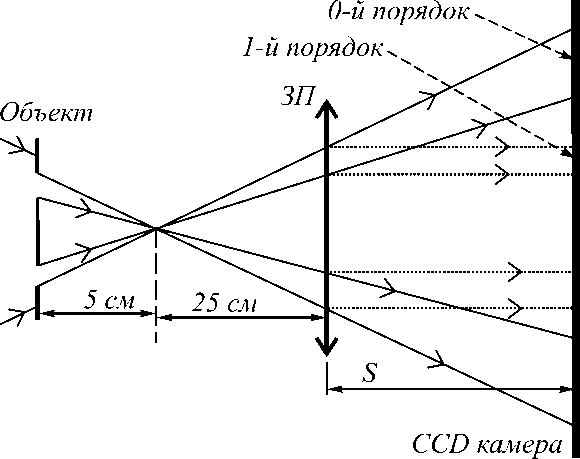
Рис. 3. Оптическая схема для построения изображения с помощью ЗП

Объект был освещён сходящимся рентгеновским пучком. Сходящийся пучок рентгеновского излучения можно сформировать, например, с помощью капиллярной линзы Кумахова [13, 14]. В качестве объектов для изображения были взяты две квадратные диафрагмы со стороной 10 мкм и расстоянием между ними 15 мкм. Таким образом, размер пятикратно увеличенного изображения составил 175 мкм. Так как ЗП имеет эффективность всего несколько процентов, в плоскость наблюдения попадёт как расходящийся падающий пучок (нулевой порядок), так и параллельный пу- чок после зонной пластинки (первый порядок). На рис. 4 представлена рассчитанная интенсивность излучения для расстояния S =25 см и S =50 см.

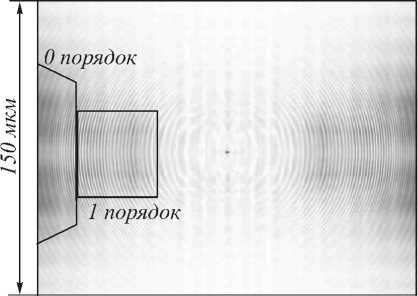
На рис. 4 а в плоскости действительного изображения не видно квадратных диафрагм из-за наложения падающего пучка на изображение расходящегося пучка. На рис. 4 б расходящийся пучок уже не попадает на изображение двух квадратных диафрагм и их отчётливо видно. Заметим, что на рис. 4 а , б всё поле интенсивности (201×201 мкм) промодулирова-но концентрическими полосами от ЗП, которые объясняются тем, что ЗП не только фазовый объект, но и амплитудный из-за частичного поглощения рентгеновского излучения в ЗП.

200 мкм

• а)

  

  200 мкм

  Рис. 4. Увеличенное в 5 раз изображение двух квадратных диафрагм на расстоянии S = 25 см (а) и S = 50 см (б) (негатив)

  
  

• б)

Для представленной на рис. 3 оптической схемы расстояние от ЗП до плоскости сфокусированного изображения равно 150 см. Рентгеновское излучение с данной длиной волны имеет сильное затухание в воздухе (затухание вдвое примерно на расстоянии 30 см), однако использование чувствительной камеры позволяет получать изображения на таком расстоянии. На рис. 5 представлено изображение двух квадратных диафрагм на расстоянии S = 150 см. Видно, что в плоскости сфокусированного изображения объекты имеют чёткие края.

Для корректной работы ЗП необходимо использовать когерентное излучение. Ограниченная поперечная когерентность отрицательно влияет на сформированное изображение. На рис. 6 приведены изображения квадратных диафрагм на расстоянии S = 50 см при пятне когерентности диаметром 20 мкм, 10 мкм, 5 мкм и 3 мкм. Размер пятна когерентности менялся в плоскости изображаемых диафрагм.

а)

б)

в)

г)

Рис. 6. Изображения квадратных апертур (негатив), полученные с помощью ЗП при частично когерентном излучении с пятном когерентности: 20 мкм (а), 10 мкм (б), 5 мкм (в), 3 мкм (г). Ширина изображений также, как и на рис. 3, равна 200 мкм, высота 130 мкм, расстояние до плоскости наблюдения S=50 см

50 мкм

Рис. 5. Увеличенное в 5 раз изображение двух квадратных диафрагм на расстоянии S = 150 см (негатив)

На рис. 6 видно, что при пятне когерентности с размером, сопоставимым с размером диафрагмы и менее, появляется тенденция к ухудшению качества изображения. Эта тенденция проявляется при формировании несфокусированного изображения объектов. Формирование несфокусированного изображения рассматривалось с целью уменьшения размеров оптической схемы.

Для проверки правильности расчётов результаты моделирования были сравнены с экспериментом из работы [9]. В [9] были получены увеличенные изображения в мягком рентгеновском излучении субмикронных дифракционных решёток с размером линий 25 и 30 нм. В данной работе был произведён расчёт ЗП с такими же параметрами, как в [9]: радиус ЗП – 30 мкм, ширина крайней зоны – 50 нм, фокусное расстояние зонной пластинки – 900 мкм, длина волны рентгеновского излучения λ = 3,37 нм, расчётное увеличение изображения – 1160 раз (расстояние между изображаемым объектом и ЗП составляло 900,7758 мкм, между ЗП и плоскостью наблюдения – 1,044983 м). Авторами в [9] с помощью такой ЗП были получены изображения линий дифракционной решётки, то есть были разрешены структуры периодом 100 нм и более, но не были разрешены структуры с периодом 50-60 нм (рис. 7).

Рис. 7. Экспериментальные изображения дифракционных решёток с шириной линии 25 и 30 нм, полученные в [9].

В области (б) представлено изображение дифракционных решёток, полученное с помощью описанной выше ЗП. Изображение в области (а) более высокого разрешения тех же частей дифракционных решёток получено с использованием другой более высокоразрешающей ЗП

На рис. 8 показан внешний вид изображаемого объекта для проведения сравнительного модели- рования.

Рис. 8. Амплитудный объект, состоящий из решёток с периодом 50 нм (а) и 100 нм (б)

Изображаемая дифракционная решётка состоит из двух частей, ширина линий в области ( а ) составляет 25 нм, ширина линий в области ( б ) – 50 нм. Для моделирования была взята сетка размером 2400×2400 отсчётов, размер отсчёта был равен 25 нм. В плоскости изображаемого объекта дискретизация сетки отсчётов была улучшена в 10 раз, то есть размер отсчёта составлял 2,5 нм. Для моделирования было использовано 640 процессоров суперкомпьютерного центра «Сергей Королёв», время моделирования приблизительно 1,5 часа.

На рис. 9 показано распределение интенсивности когерентного рентгеновского излучения в плоскости наблюдения после прохождения через элемент, изображённый на рис. 8 (негатив).

Интенсивность, отн. ед.

1,0

0,8

0,6

0,4

0,2

О

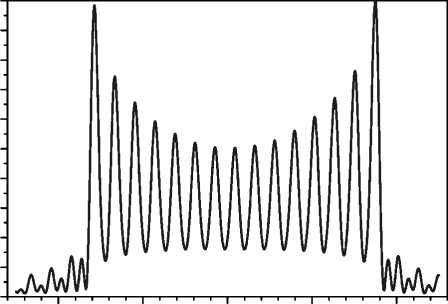
б)       -1000   -500     0     500 R, мкм

Рис. 9. Распределение интенсивности (негатив) в плоскости наблюдения (а) и сечение по вертикальной светлой линии (б)

На рис. 9 видно, что линии дифракционной решётки в области ( б ) с периодом 100 нм разрешились удовлетворительно, в то время как линии в области ( а ) с периодом 50 нм не разрешились, что согласуется с экспериментальным результатом из [9]. Период линий в области ( б ) в плоскости изображения составляет примерно 116 мкм, что соответствует увеличению 1160 раз исходного изображаемого объекта, изображены все 15 линий решётки.

Заключение

В работе продемонстрировано формирование увеличенного изображения в сходящемся пучке рентгеновского излучения с помощью ЗП, которая была экспериментально изготовлена в [9, 11]. Как показало моделирование, при данной оптической схеме увеличение составляет 5 раз. Для получения изображения источника (квадратных апертур) камеру необходимо располагать на некотором отдалении S от зонной пластинки, чтобы прямое излучение от источника разошлось за пределы области диаметром ЗП (200 мкм). Это обусловлено тем, что эффективность фокусировки света зонной пластинкой составляет всего 4%.

Моделирование показало, что при частично когерентном источнике излучения пятно когерентности должно быть сопоставимо с размером изображаемых объектов (или более).

Моделирование эксперимента по изображению дифракционных решёток, описанного в [9], показало, чтодифракционная решётка с периодом 100 нм разрешилась с высоким контрастом (более 0,5) ЗП с шириной крайней зоны 50 нм.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), грантов Президента РФ поддержки ведущих научных школ (НШ-7414.2010.9), молодого кандидата наук (МК-64571.2010.2), молодого доктора наук (МД-8026.2010.2).