Моделирование формирования кластерных групп углерода в плазме электродугового разряда

Получение углеродных наноструктур (УНС) обладающих уникальными механическими и электрическими свойствами, является перспективных направлений развития современной науки. Использование их, например, в качестве добавок в полимерные смолы, позволяет создавать полимерные нанокомпозиты, обладающие новым или улучшенным комплексом свойств [1] .

Промышленное производство УНС (фуллеренов, нанотрубок, нановолокон) сдерживает низкая производительность и высокая стоимость существующих технологий синтеза, обусловленные недостаточностью изученности особенностей процесса их образования.

На сегодняшний момент нет единого мнения о модели формирования УНС.

Понимание механизма образования кластерных групп углерода формирующих объемные УНС позволит исследователям целенаправленно создавать и варьировать способами и условиями получения различных типов наноструктур и их производных, что позволит значительно повысить эффективность существующих технологий синтеза.

В основном применяемые в промышленности технологии синтеза УНС предполагают использование различных методов термического испарения атомарного графита энергетическим потоком или разложение углеродосодержащих газов с последующим осаждение формируемых

структур на охлаждаемую поверхность [2] . Во всех технологиях происходит термическое разрушение структуры исходного материала с последующим образованием и ростом многоатомных кластеров углерода с различными типами связей, которые и формируют объемные УНС.

Одним из наиболее распространенных методов синтеза УНС является метод термического испарения графита плазмой дугового разряда в среде буферного газа [3] . Данный метод позволяет вовлекать в технологический процесс значительные объемы сырья и отличается высокой скоростью протекания и качеством конечного продукта.

Изучение отдельных физико-химических процессов, протекающих при горении дуги, охватывает исследование электрических, тепловых, диффузионных, газодинамических и плазменных явлений. Каждое из этих явлений достаточно подробно изучено и описано, однако в реальном процессе дугового синтеза УНС происходит одновременно множество взаимодействующих явлений с определенными особенностями, разделить которые зачастую невозможно, поэтому использовать существующие математические модели для описания движения и взаимодействия частиц в плазме невозможно.

Для описания поведения низкотемпературной плазмы существует также разные подходы к её математическому моделированию: одночастичное приближение, метод молекулярной динамики, магнитогидродинамическое, кинетическое описание, метод Монте-Карло, шредингеровские модели [4] . Перечисленные подходы отличаются степенью детализации компонентов плазмы, вычислительными затратами и возможностью учета необходимых особенностей рассматриваемого процесса.

Наибольший интерес для моделирования динамики плазмы применительно к электродуго-вому синтезу, представляют инструментальные средства кинетической теории на основе уравнения Больцмана. Использование функций распределения заряженных частиц по координатам и импульсам позволяет учитывать разнообразие происходящих процессов в плазме и снизить вычислительную сложность моделирования.

• 1.1    Постановка задачи

Целью данной работы является разработка математической модели процессов синтеза различных УНС в плазме электродугового разряда, позволяющей описывать механизм образования и рост углеродных кластерных групп с различными типами связей (С–С, С =С (С2) и С =С–С (С3)), которые являются основой построения объемных наноструктур. При этом необходимо учитывать все основные факторы процессов синтеза, влияющих на движение и столкновения частиц в межэлектродном пространстве. В модели должны учитываться парные упругие и неупругие столкновения различных частиц многокомпонентной плазмы.

1.1.1    Математическая модель движения и взаимодействия частиц в плазме

В основу предлагаемой математической модели описывающей движения частиц многокомпонентной плазме с учетом взаимодействий между ними, положена система уравнений Больцмана [5] для каждого вида частиц, дополненная условием парных столкновений между частицами:

dfa+S dfa - a (E+1[S, Ь ]) da =f dt     dr   ma С dS   9t

, (1)

СТ

где fα, fα′ –функции распределения компонент плазмы до и после столкновения (α: e – электрон, h – ион буферного газа (Не), с – ион углерода); r - координаты частицы; qa, ma - заряд и масса частицы.

Допуская, что столкновения в плазме дугового разряда происходят между электронами, ионами буферного газа и частицами углерода интегралы парных столкновений запишутся в виде:

f^  = I   jj ( fa fв" faf_B )I* S - ' S' Idad5^', (2)

∂t СТ β=e,c,hV     β β где S, S' - скорости частиц до и после столкновения; dσ= 4R1R2cosθdΩ – дифференциальное эффективное сечение рассеяния частиц R1 и R2 в телесный угол dΩ ; θ – угол между скоростью сталкивающихся частиц и линией движения.

Система уравнения (1) с целью нахождения параметров электромагнитного поля дополняется системой уравнений Максвелла описывающих самосогласованное поле [6] .

В качестве функции описывающей распределение частиц по скоростям в плазме, задается распределение Максвелла. Начальные и граничные условия представлены в работе [7] .

Использование в уравнении (1) интеграла столкновений (2) вызывает значительные сложности в явном решении данной задачи. Поэтому интеграл столкновений (2) можно представить в виде уравнения Фоккера–Планка, записанного для рассматриваемого примера в виде:

∂ ^{f α} = ¹ ∂ ²    f ∆∂ ϑ ∆∂ ϑ   -

∂ t _СТ 2 ∂ ϑ _r ∂ ϑ _v ^{α rv α} -∂ ϑ ∂ ( f α ∆∂ ϑ r α ) ,

где ∂ϑr , ∂ϑv – компоненты скорости частиц в декартовых координатах.

При расчете средних значений прироста в единицу времени компонент скорости α частицы (Aд O_r ) и^Aд O_r Aд O_v ^ делается предполо-

где G _a , C _a , R _a - матрицы безразмерных коэф

жение, что изменения в скорости есть результат взаимодействий двух частиц, их столкновений, во время которых пространственные корреляционные эффекты не имеютзначения. Поэтому выражения для ^Aд O_r ) и ^Aд O_r Aд O_v ^ можно

фициентов размерностью (3^Х1); K _a - параметрический коэффициент.

Итоговая система уравнений (1) описыва-

ющих кинетику движения заряженных частиц в трехкомпонентной плазме дугового разряда с учетом интеграла столкновений (7) в безраз-

мерном виде примет вид:

представить в виде:

{A69r X = Z Jfb (o’)d^J^(u,Q)uAdQ, k=e, с, h

{A69 _r AдO _v }_a = Z J fb O', ) d o , J ^ ( u ) u Ao , AдO _v d Q , k = e , с , h

ˆ

L_ + д t

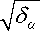
дf a ₊ Z a р

1 E д r   2s _a

дf a do ,

где u = I O r - O r |; O r , O , - скорости частиц до

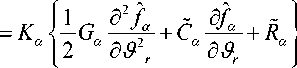
где 5_a , £_a - безразмерные коэффициенты.

и после столкновения.

Переход к декартовой системе координат с единичными векторами, позволяет вычислить изменения относительной скорости в локальной системе для всех столкновений с помощью

Используя метод расщепления. конечная система уравнений разбивается на две вспомо-

интегрирования по углам рассеяния.

Пренебрегая слабой зависимостью от u , получаем:

<^oa. и fb wml -° (^>.

b = e , i , h                                         ^dO r

₂                                (5)

(AdO AdO =Г„ (—g^-), r va     ^Odo doj где Z – коэффициент кратности заряда; Га - коэффициент связанности.

Подставляя в уравнение (3) уравнения (5) получаем уравнение Фоккера-Планка для произвольной функции распределения компонент плазмы α :

±^df a ) = 1 d 2 f f ⁹ 2 § « ) г a (a t) СТ 2 ao r ao v ( ^J“ ao r ao v J

гательных задачи: одна определяет перенос частиц, вторая столкновение заряженных частиц, которые решаются последовательно.

Наличие большого количества частиц (10¹⁵ ÷ 10¹⁷ штук) каждой компоненты плазмы, участвующих в расчете на каждом временном шаге, вызывает необходимость использования для численного решения системы уравнений Больцмана–Максвелла метода «крупных частиц» [8] , позволяющего снизить объем вычислений и требования к компьютерным ресурсам, за счет уменьшения количества однотипных частиц в расчете, путем их группировки до обоснованного уровня в макрочастицы не влияющей на точность расчетов.

Для выполнения численных расчетов по построенной модели, была использована технологий параллельных вычислений на СРU и GPU [9] . Использование технологии GPU

позволило выполнить вычисления неспециали-

—

h a = Z b

,

m a + m b

f b

mb

I o _a — o ;|

do ; ,

g a = ZJ f b o « — o ; | do ; ,

b

где m _α, m_b – массы двух сталкивающихся частиц a и b .

Уравнение (6) можно записать в виде тензоров. Расписывая ковариантные тензорные производные и опуская промежуточные преобразования перехода к декартовой системе координат получим конечное уравнение интеграла столкновений в безразмерном виде:

ˆ

(^ f TJ

V J ст

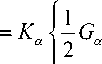
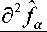
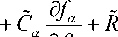
a

^ (7)

зированных потоков на аппаратно-программном комплексе CUDA (Compute Unified Device Architecture) с применением технологии nVidiа CUDA [10] . Данная технология позволяет использовать графические процессоры для вычислений общего назначения на одном ПК, что значительно повышает эффективность обработки больших объемов данных без использования суперЭВМ или вычислительных кластеров.

Для решения задачи поиска столкновений частиц был разработан специальный алгоритм, заключающийся в проверке факта пересечения траекторий объектов в пространстве.

1.2 Результаты исследований

В процессе моделирования определялись зоны и состояния удовлетворяющее пространственным и энергетическим условиям вероятного формирования кластерных групп углерода со связями типов С 2 и С 3 , нарастание которых образует линейные углеродные цепочки замыкающиеся

в моноциклические кольца (пентагоны и гексагоны) формирующие выпуклые структуры углерода (фуллерены, нанотрубки) как в плазме, так и на катоде.

Для проведения исследований по модели были выбраны два основных режима синтеза УНС: режим образования катодного депозита с максимальным содержанием нанотрубок (режим «Нанотрубки»)(сила тока дуги 150 А) и режим с максимальным входом фуллеренов осаждающихся на стенки камеры в виде сажи (сила тока 350А)(режим «Фуллерены»). Остальные параметры расчета: межэлектродное расстояние 1 мм, диаметр электродов 12 мм, напряжение между электродами 25 В, давление буферного газа гелия в камере синтеза 400 Торр.

Для подтверждения адекватности модели, была выполнена аналогичная серия экспериментов на лабораторной установке синтеза УНС с автоматизированной системой управления процессом, позволяющей поддерживать постоянные технологические параметры синтеза. Результаты экспериментальных исследований и численных расчетов осаждения частиц углерода на катод в виде депозитного осадка по разработанной модели, при одних и параметрах процесса синтеза представлены на рисунке 1.

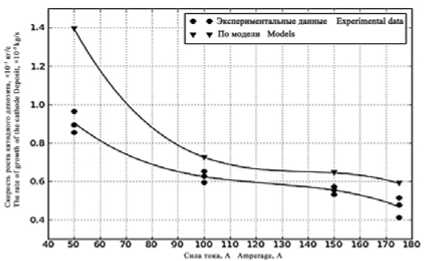
Рисунок 1. Экспериментальные и расчетные значения скорости роста катодного депозита в зависимости от силы тока Figure 1. Experimental and calculated values of the cathode Deposit growth rate depending on the current strength

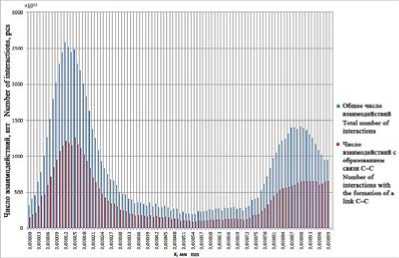
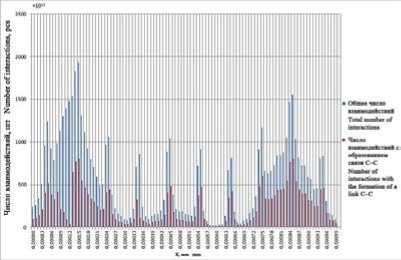
Результаты расчета количественных характеристик общих парных взаимодействий ионов углерода с образованием устойчивых линейных связей С2 и С3 в плазме межэлектродного пространства представлены на рисунках 2–4. Временной интервал выполненных расчетов составляет 360 нс.

Общее количество столкновений частиц определяется концентрацией частиц, их скоростью, размером и оказывает непосредственное влияние на образование кластеров. Соотношение числа столкновений с образованием связей к общему числу столкновений в исследованных условиях изменяется не значительно.

Анализ выполненных численных расчетов по модели показывает, что формирование кластерных групп углерода С 2 и С 3 в процессе электродугового синтеза в рассматриваемых режимах происходит во всем межэлектродном пространстве с различной интенсивностью.

Это объясняется различными параметрами электромагнитных полей ускоряющих частицы, температурой плазмы и различными начальными скоростями частиц. Наибольшее количество взаимодействий частиц углерода и соответственно образование устойчивых связей происходит в первой и последней четверти межэлектродного пространства.

На начальном этапе имеется наибольшее количество частиц с относительно невысокой скоростью. И большое количество частиц дает большое число столкновений, часть из которых приводит к образованию устойчивых связей и укрупнению частиц. При движении частицы увеличиваются в размерах за счет образования связей при столкновениях с другими частицами, разгоняются под воздействием электрического поля, но общее количество частиц уменьшается. Количество частиц уменьшается, уменьшается их концентрация, что ведет к уменьшению общего числа столкновений и образованию кластеров. Далее образовавшиеся кластеры разгоняются электромагнитным полем, что приводит к увеличению общего числа столкновений в прикатодной области, а, следовательно, и количества образующихся связей.

(a)                                                                     (b)

Рисунок 2. Общее число парных столкновений ионов углерода в плазме и образование связей С–С, в режимах синтеза «Нанотрубки»(a) и «Фуллерены»(b)

Figure 2. Total number of paired collisions of carbon ions in plasma and formation of bonds С–С, in the modes of synthesis of «Nanotubes»(a) and «Buckyballs»(b)

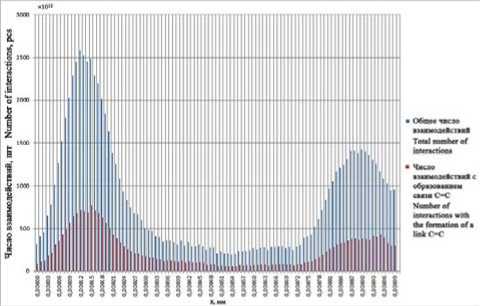
(a)

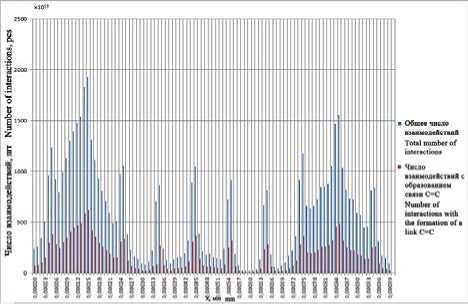
(b)

Рисунок 3. Общее число парных столкновений ионов углерода в плазме и образование связей С = С, в режимах синтеза «Нанотрубки» (a) и «Фуллерены» (b)

Figure 3. Total number of paired collisions of carbon ions in plasma and formation of bonds С = С, in the modes of synthesis of «Nanotubes» (a) and «Buckyballs» (b)

(a)

(b)

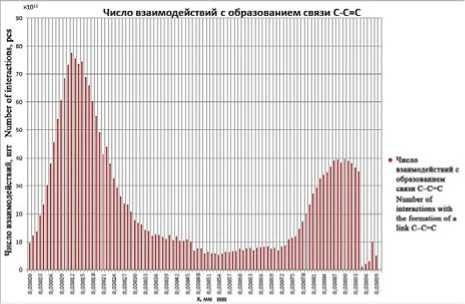
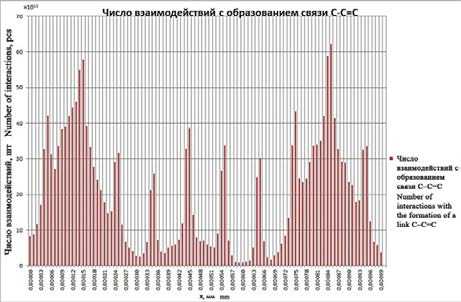
Рисунок 4. Образование связей С =С-С в режимах синтеза «Нанотрубки»(a) и «Фуллерены»(b)

Figure 4. The formation of bonds C =C-C modes of the synthesis of «Nanotubes»(a) and «Buckyballs»(b)

На количество и характер взаимодействий ионов углерода в плазме непосредственное влияние оказывает сила тока дуги, которая определяет в плазме параметры электромагнитного и температурногополей действующих на частицы. Количество образуемых в плазме кластерных групп углерода С3 по сравнению с С 2 существенно меньше, что объясняется недостаточностью суммарной кинетической энергией взаимодействующих частиц для активации химической связи.

Промежуточные пики столкновений, полученные в режиме«Фуллерены» объясняется дискретностью представления испарения графита с анода при численных расчетах. Однако расчеты показывают, что в данном режиме образование связей между атомами углерода идет более интенсивно идет по всей длине межэлектродного пространства, что приводит к синтезу фуллеренов в плазме, без осаждения на катод.

Таким образом, разработанная модель позволяет моделировать формирование углеродных наноструктур в плазме электродугового разряда с учетом их особенностей синтеза.

Выводы

Предложенная методика моделирования движения и взаимодействия заряженных частиц в многокомпонентной плазме электродугового разряда на основе системы уравнений Больцмана-Максвелла, с учетом парных упругих и неупругих взаимодействий между частицами позволяет учитывать процессы, протекающие в плазме и рассчитывать параметры образующихся межатомных связей.

Выполнены исследования на основе полученной модели количества парных столкновений ионов углерода в плазме с образование ковалентных связей типа С–С, С =С и С =С–С в различных режимах синтеза, что позволило сделать вывод, что образование кластеров в плазме происходит во всем межэлектродном пространстве с различной интенсивностью и зависит от параметров процесса. Разработанная математическая модель может быть использована при расчете параметров технологического процесса синтеза углеродных наноструктур, а также управлении процессом.