Моделирование генерации оптических вихрей с помощью спиральной зонной пластинки из серебра

С момента появления в оптике понятия орбитального углового момента (ОУМ) прошло более 25 лет [1], но до сих пор вихревые лазерные пучки, несущие ОУМ, не потеряли своей актуальности. Большое количество современных работ посвящены изучению оптических вихрей [2–4]. Интерес к подобного рода пучкам связан с большим количеством различных приложений, где они могут быть использованы. Оптические вихри, у которых в процессе распространения в свободном пространстве поперечное распределение интенсивности светового поля вращается вокруг оптической оси, широко используются в микроскопии в ходе измерения положения и ориентации молекул [5], в зондировании атмосферы и беспроводных коммуникационных системах [6], подводных системах передачи информации [7], а также в фиксации магнитных полей [8].

Для генерации оптических вихрей разрабатываются специальные оптические элементы [9–19]. Исследование и экспериментальная демонстрация генерации трехмерных объемных оптических вихрей на основе взаимодействия света с высокоэффективной диэлектрической метаповерхностью представлены в [9]. Несколько оптических вихрей с топологическими зарядами 2, 4, 6 формируются в различных порядках дифракции нанопластинки из аморфного кремния (коэффициент преломления n = 3,9231 + i 0,1306 для длины волны 780 нм) с размерами 410×175×466 нм и периодом 600 нм. Серия фазовых элементов Панчаратнам– Берри разработана в [10] для создания идеальных вихревых и векторных пучков. Векторные пучки на длине волны 633 нм с топологическими зарядами 1, 2, 3 и кольцевой структурой, диаметр которой не зависит от топологического заряда, формируются спиральной зонной пластинкой (СЗП), аксиконом и зонной пла-

6179-2018-42-6-977-984.

стиной (ЗП). Размер элементов был 6 мм, а фокусное расстояние линз составило 200 мм. С помощью FDTD-метода показано, что спиральная металинза из аморфного кремния с единичным топологическим зарядом и числовой апертурой (NA= 1) может остро сфокусировать оптический вихрь [11]. Дифракционный элемент для генерации оптических вихрей, основанный на фазовой модификации радиального смещения зон, был представлен в [12]. Роль так называемого параметра сдвига была также исследована, и в результате показано, что он является параметром регулирования размера вихря. Все результаты были проверены экспериментально, и продемонстрирована высокая степень соответствия теоретических и экспериментальных данных. В [13] рассматриваются децентрированные фазовые СЗП с дробным топологическим зарядом. В [14] показано, что использование СЗП с дробным топологическим зарядом и контроль начальной ее ориентации позволяет разрушить симметрию процесса фокусировки и получить ориентационно-селективные анизотропные вихревые фокусы. Численные результаты показывают, что бинарная структура элемента дает дополнительные высокоуровневые фокусы на оптической оси, а интенсивность в фокусе зависит от топологического заряда. В [15] теоретически и экспериментально исследуется спиральная фазово смещенная ЗП, позволяющая генерировать различные оптические вихри с заданным топологическим зарядом. Показано, что количество спиральных рукавов, также и спиральная кривизна импульса, зависят от параметра сдвига СЗП. Кроме того, показано, что до и после плоскости фокусировки формируются вихри с разными топологическими зарядами, при этом топологический заряд оптического вихря до фокуса постепенно трансформируется, чтобы образовать новый оптический вихрь после фокуса. В [16] теоретически и численно исследуются пространственно-временные характеристики ультракоротких оптических вихрей, такие как распределения интенсивности, фазы, ОУМ и потока энергии. Ультракороткий вихревой импульс формируется с помощью спиральной ЗП с набором отверстий, которая была исследована с использованием интерферометрической системы Маха–Цендера. В [17] на базе СЗП и дифракционных структур с синусоидальной функцией пропускания области зон был спроектирован оптический элемент, который имеет возможность формировать однофокусную фазовую сингулярность.

В данной статье рассматривается генерация оптических вихрей с помощью амплитудной СЗП в тонкой серебряной пленке, напылённой на кварцевое стекло. Моделирование проводилось FDTD-методом с учетом зависимости диэлектрической проницаемости от частоты ((FD)2TD-методом), который реализован в пакете FullWAVE (RSoft). В качестве падающего излучения рассматривался Гауссов пучок с круговой поляризацией и длиной волны λ = 532 нм. Для подробного изучения процесса генерации рассматривалась левая и правая круговая поляризация. В ходе моделирования были рассчитаны распределения фазы и амплитуды для каждой компоненты напряженности электрического поля, а также распределение интенсивности. Кроме того, рассматривалось распределение вектора Умова–Поинтинга, который показал наличие обратного потока энергии в области фокуса.

Формирование оптического вихря фазовой СЗП

Хорошо известно, что СЗП могут быть использованы для генерации и фокусировки оптических вихрей. Функция пропуская бинарной СЗП может быть записана следующим образом:

T ( r , 3 ) = sgn I cos

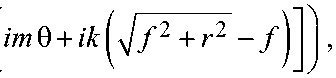
где sgn x =(1, x >0; –1, x <0), r и θ – полярные координаты, k – волновое число, f – фокусное расстояние. Рис. 1 демонстрирует бинарный шаблон рассматриваемой СЗП ( а ) и оптическую схему численного моделирования ( б ). Радиус элемента был выбран равным 4 мкм, а фокальное расстояние равно длине волны падающего излучения X = 532 нм. Топологический заряд СЗП составил m =2.

Гауссов пучок с круговой поляризацией, длиной волны 532 нм и радиусом перетяжки 3 мкм был выбран в качестве падающего излучения. Оба типа круговой поляризации: левая (ЛКП) и правая (ПКП) – использовались в ходе данного исследования. Для расчета пространственного распределения интенсивности входного излучения с требуемой поляризацией использовался MATLAB. 2D-проекция интенсивности падающего излучения на шаблон оптического элемента представлена на рис. 1 б .

Фазовая СЗП, выполненная из кварцевого стекла, высота рельефа h = X = 532 нм, рассматривалась как эталонный образец для сравнения. Для кварцевого стекла использовалась модель дисперсии Селлмейера [18]. Параметры модели были взяты из работы [18].

у, мкм

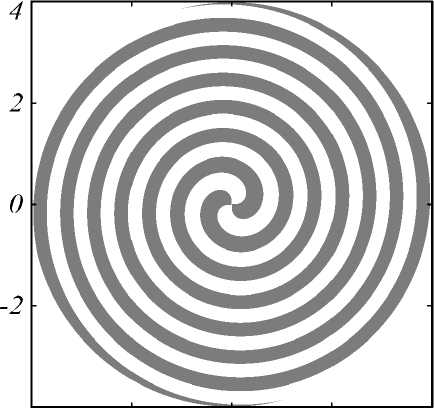
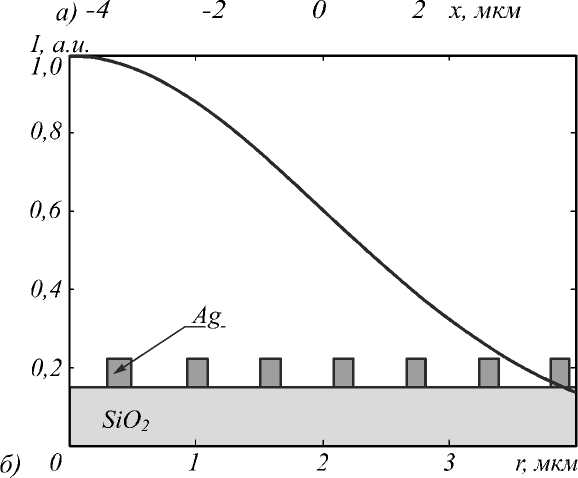
Рис. 1. Шаблон СЗП в поперечной (а) и продольной (б) плоскостях. Черная линия отображает распределение интенсивности в падающем излучении

Моделирование проводилось с помощью (FD)²TD-метода, реализованного в пакете FullWAVE (RSoft). При расчетах использовались следующие параметры сетки: шаги по поперечным и продольной координатам составили 15 нм и 7 нм соответственно. Шаг по псевдовремени c Δ t был выбран равным 5 нм в соответствии с условием Куранта. Данные шаги гарантируют сходимость численного метода, а их дальнейшее измельчение не приводит к значительным изменениям в результатах моделирования (стандартное отклонение 0,001%).

Для более детального исследования полученных результатов для каждой компоненты электрического поля, формируемого в фокальной плоскости элемента в момент времени cT = 19,82 мкм, с помощью MATLAB были расcчитаны амплитуда и фаза, распределения которых представлены на рис. 2–4.

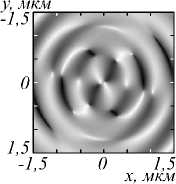
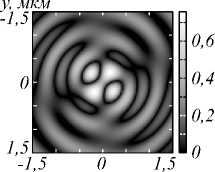
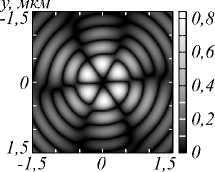
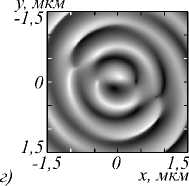
Из рис. 2 –4 видно, что СЗП с m = 2 формирует оптический вихрь со сложным топологическим зарядом: поперечные компоненты ( E x и E y ) имеют топологический заряд m = 2, в то время как продольная компонента ( E z ) имеет m = 3 для ЛКП и m = 1 для ПКП. Разница в топологических зарядах может быть объяснена тем фактом, что направления закрутки спирали СЗП и колебаний падающего излучения совпадают в случае КПК и противоположны друг другу в случае ЛКП [11].

б)

V. МК.М "-L5V7

1,5 V . . ___,___ ,___ZJ . -1,5       0       1,5

г)                   -Y, ЛПСМ

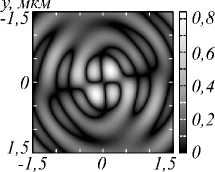
Рис. 2. Распределение амплитуды (а, в) и фазы (б, г) для компоненты Ex электрического поля, сформированного в фокальной плоскости (f = 532 нм) фазовой СЗП в ходе распространения Гауссова пучка с ЛКП (а, б) и ПКП (в, г)

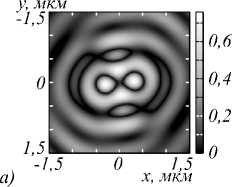
Рис. 3. Распределение амплитуды (а, в) и фазы (б, г) для компоненты Ey электрического поля, сформированного в фокальной плоскости (f = 532 нм) фазовой СЗП

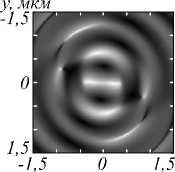
в ходе распространения Гауссова пучка с ЛКП (а, б) и ПКП (в, г)

б)

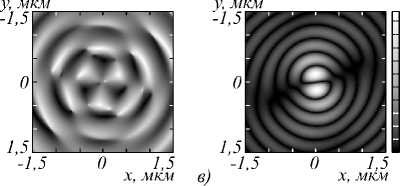
Рис. 4. Распределение амплитуды (а, в) и фазы (б, г) для компоненты Ez электрического поля, сформированного в фокальной плоскости (f = 532 нм) фазовой СЗП в ходе распространения Гауссова пучка с ЛКП (а, б) и ПКП (в, г)

1.0

0,8

0,6

0,4

0,2 О

Формирование оптического вихря амплитудной СЗП

В [20] показано, что амплитудная ЗП может формировать аналогичные дифракционные картины, что и фазовая ЗП. Основное различие между полученными распределениями заключается в величине максимальной интенсивности. Однако для получения подобных результатов необходимо подобрать высоту металлического рельефа. Так, в [21] показано, что серебряная ЗП с выстой рельефа 100 нм дает наиболее подходящее фокальное пятно.

В данной работе также была проведена серия численных экспериментов для выбора оптимальной высоты рельефа для серебряной СЗП. Для описания зависимости диэлектрической проницаемости от высоты использовалась модель Друде–Лоренца с параметрами из [22]. Параметром для оценки качества результата работы СЗП выступала максимальная интенсивность. Результаты численного моделирования представлены в табл. 1.

Из табл. 1 видно, что высота рельефа в 20 нм слишком мала и является достаточно прозрачной для падающего излучения, поэтому не может сфокусировать его. В то же время высота в 200 нм достаточно велика и приводит к большим потерям в энергии светового пучка. Таким образом, из табл. 1 видно, что высота рельефа h = 100 нм позволяет получить в фокусе максимальную интенсивность, которая лишь в два раза меньше максимальной интенсивности, формируемой фазовой СЗП. Результаты, представленные в табл. 1, согласуются с выводами, полученными в [21]. Таким образом, в данной работе высота серебряной пленки для изготовления рельефа была выбрана равной 100 нм для достижения аналогичных результатов, как и в случае фазовой СЗП. Кроме того, стоит отметить, что изготовление амплитудной СЗП представляется более легкой задачей, нежели травление фазовой СЗП с высотой рельефа 532 нм.

Табл 1. Результаты моделирования для амплитудной СЗП

h , нм	Imax , a.u.
	ЛКП	ПКП
20	3,1195	3,3831
100	4,1740	5,2285
200	3,7346	4,7452

Рис. 5– 7 показывают распределение амплитуды и фазы элемента оптического вихря в фокальной плоскости в момент псевдовремени cT = 19,82 мкм.

:. мкм

Рис. 5 – 7 демонстрируют аналогичные результаты для амплитудных и фазовых распределений формируемых оптических вихрей, что подтверждает возможность использования серебряной СЗП для их генерации. Стоит отметить: несмотря на то, что в работе не проводилось подробное исследование плазмонных эффектов, из полученных

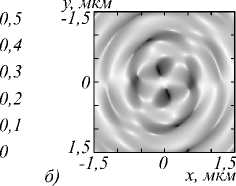
результатов моделирования видно, что они не имеют большого влияния на процесс формирования оптических вихрей, как это было показано и для ЗП с m = 0 [11].

На рис. 8 представлено двумерное распределение интенсивности поля в фокальной плоскости, а на рис. 9 их сечения по осям X и Y.

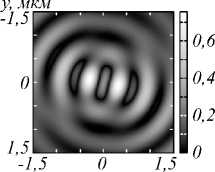
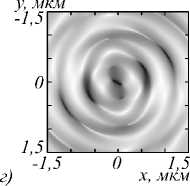
Рис. 5. Распределение амплитуды (а, в) и фазы (б, г) для компоненты E x электрического поля, сформированного в фокальной плоскости (f = 532 нм) амплитудной СЗП (рис. 1) в ходе распространения Гауссова пучка с ЛКП (а, б) и ПКП (в, г)

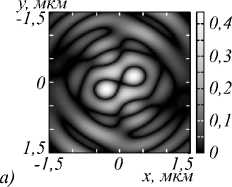
Рис. 6. Распределение амплитуды (а,в) и фазы (б,г) для компоненты E y электрического поля, сформированного в фокальной плоскости (f = 532 нм) амплитудной СЗП (рис. 1) в ходе распространения Гауссова пучка с ЛКП (а, б) и ПКП (в, г)

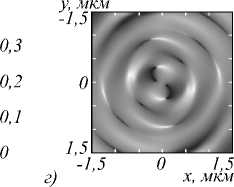
-1.5       0      1,5             -1,5       0      1,5    , -1,5       0       1,5             -1,5       0      1,5

а)              х, мкм       б)              х, мкм в)              х, мкм       г)              X, мкм

Рис. 7. Распределение амплитуды (а, в) и фазы (б, г) для компоненты E z электрического поля, сформированного в фокальной плоскости (f = 532 нм) амплитудной СЗП (рис. 1) в ходе распространения Гауссова пучка с ЛКП (а, б) и ПКП (в, г)

У

О

-2

-4

а)     -4        -2        0         2         4

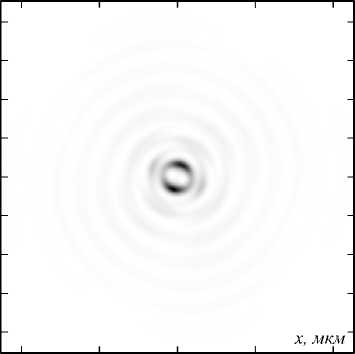
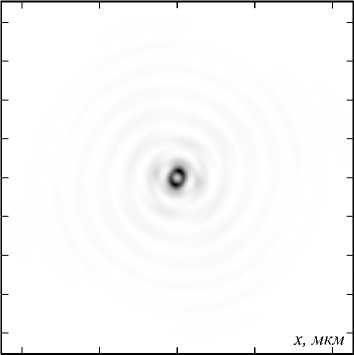
Рис. 8. Распределение интенсивности в фокальной плоскости амплитудной СЗП (рис. 1) для Гауссова пучка с ЛКП (а) и ПКП (б)

мкм

О

-2

-4

О

б)     -4        -2        0         2         4

Из рис. 8 видно, что в фокусе формируется кольцо, максимальная интенсивность которого в 6 раз превосходит интенсивность падающего излучения. Однако стоит отметить, что кольцо имеет не совсем правильную форму: образуются утолщения в подобластях кольца под углом – 45 ° от оси Y. Также стоит заметить, что кольцо для пучка с ЛКП шире, чем для пучка с ПКП. Из рис. 9 видно, что ширина и радиусы световых колец равны 0,495 мкм и 0,361 мкм для ЛКП и 0,270 мкм и 0,165 мкм для

ПКП. В центре эллиптических колец наблюдается минимум.

Формирование обратного потока

В работе [24] рассматривалось поведение продольной компоненты вектора Умова– Поинтинга Sz в ходе фокусировки оптического вихря с помощью СЗП с топологическими зарядами m = ± 1 и m = ± 2. В данной работе также было проведено подобное исследование. На рис. 10 представлены итоги моделирования.

а)

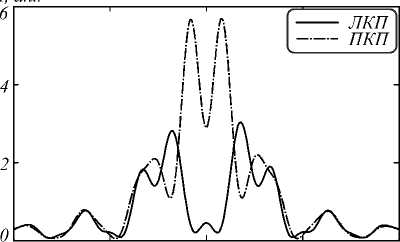
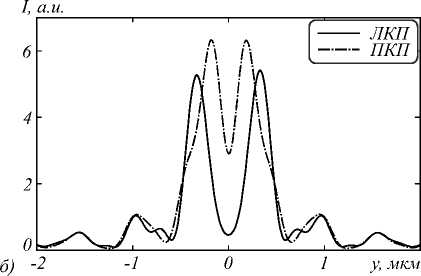
Рис. 9. Сечение интенсивности поля в фокусе амплитудной СЗП (рис. 1) при y = 0 (а) и x = 0 (б)

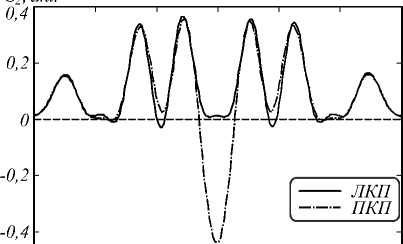
.Y, .МКМ

а)

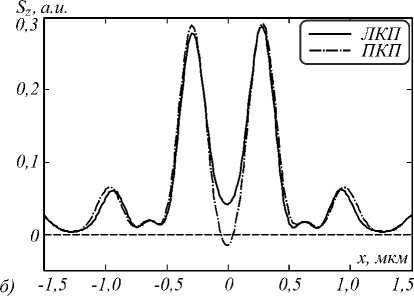
Рис. 10. Распределение продольной компоненты Умова – Поинтинга S z в фокальной плоскости для фазовой (а) и амплитудной (б) СЗП

Из рис. 10 видно, что величина обратного потока в случае серебряной СЗП значительно ниже, вплоть до полного его исчезновения для ЛКП. При этом качественно распределение продольной компоненты вектора Умова–Поинтинга Sz также претерпевает определенные изменения, а именно уменьшаются боковые лепестки.

Стоит отметить, что продольную компоненту вектора Умова–Поинтинга формируют поперечные распределения напряженности электрического и магнитного полей:

S z = Re [ E x H *y - E y H * ] . (2)

Таким образом, можно говорить о вихре второго порядка, формируемом в потоке энергии вдоль оси распространения излучения.

Заключение

В данной статье рассматривается генерация оптических вихрей с помощью амплитудной СЗП в тонкой серебряной пленке, напыленной на кварцевое стекло. Моделирование проводилось с помощью (FD)2TD-метода, который реализован в пакете FullWAVE (RSoft). В качестве падающего излучения рассматривались Гауссовы импульсы с ЛКП и ПКП, длина волны импульсов была равна длине волны зеленого лазера λ =532 нм.

В ходе анализа результатов моделирования были рассчитаны распределения фазы и амплитуды для каждой компоненты напряженности электрического поля. Было показано, что амплитудная СЗП позволяет генерировать оптические вихри, максимальная интенсивность которых в фокальной плоскости в 6 раз превышает интенсивность падающего излучения. При этом амплитудные СЗП в отличие от фазовых СЗП легче в изготовлении в связи с тем, что высота рельефа амплитудной СЗП составляет 100 нм. В работе также анализировалась продольная компонента вектора Умова – Поинтинга, которая показала наличие обратного потока энергии в области фокуса. При этом в случае использования амплитудной СЗП величина обратного потока много меньше, чем для фазовой СЗП.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Формирование оптического вихря фазовой СЗП», Российского фонда фундаментальных исследований (грант 18-07-01122, 18-07-01380) в части «Формирование оптического вихря амплитудной СЗП» и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Формирование обратного потока».