Моделирование геоэкологического риска

В опросы оценки геоэкологического риска и уровня геоэкологической безопасности на различных территориях приобрели в настоящее время статус актуальнейшей проблемы, так как инженерная геология вплотную занялась изучением динамических геологических систем в их взаимодействии со строительными системами [1, 2]. Устойчивость таких систем, их надежность и, в конечном итоге, безопасность для человека определяется механизмами взаимодействия системы с геологической средой [2 - 7]. Исследования последних лет показали, что на человека и техническое состояние разного рода сооружений в подавляющем большинстве случаев оказывают влияние аномальные деформации земной поверхности, выражающиеся в таких явлениях, как карстово-деформационные процессы, просадочно-обвальные явления, оползни, нарушенность геологической среды [4 - 6, 8 – 10].

В ряде работ авторами предложен и рассмотрен аналитический метод восстановления полей тектонических напряжений на основе анализа аномального гравитационного поля в изостатической редукции, позволяющий строить прогнозные карты потенциального геодинамического и, соответственно, геоэкологического риска с вероятностью до 0,75 для весьма протяженных территорий [12].

• ¹    – Российский новый университет, г. Москва, проректор,

• ²    – Академия ФСИН России, г. Рязань, доцент.

Имея подобные прогнозные карты, можно достаточно эффективно проводить выявление зон геоэкологического риска и выполнять оценку уровня геоэкологической безопасности на интересующей территории по отношению к такому виду «медленных» катастроф, как карстово-деформационные процессы, криповые подвижки, оседания земной поверхности в региональном масштабе [9, 11, 12].

В настоящей работе основной акцент сделан авторами на оценке комплексного геоэкологического риска ландшафтно-территориального комплекса Байкальского региона, рекреационная и хозяйственная инфраструктура которого активно развивается в последние годы.

Методика вероятностного подхода к оценке геоэкологического риска

На основании методики [12] выполнены оценки степени геоэкологического риска для территорий различного масштабного уровня, таких как Рязанская область, Республика Беларусь, отдельные участки центральной части Восточно-Европейской платформы [12], а также для локальных строительных объектов [13]. Все указанные территории относятся к областям платформенного типа, на которых диа-

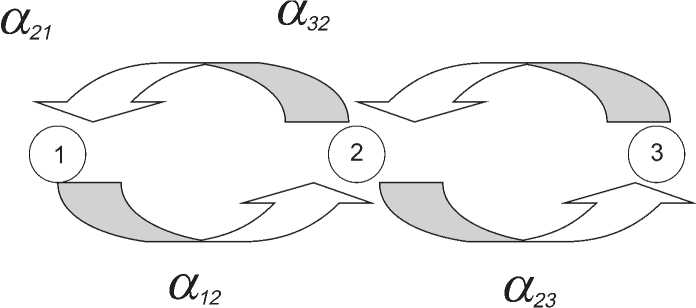
Рис. 1. Схема взаимопереходов системы ландшафтно-территориального комплекса по геоэкологическим состояниям 1, 2, 3.

пазон величин плотности потенциальной энергии деформируемых пород геосреды E_ρ не столь значителен (порядка 0 – 20 Дж/(м ³ ×год).

Вместе с тем достаточно хорошо известно, что территория, непосредственно прилегающая к озеру Байкал, да и сама акватория озера являются в высокой степени сейсмически активными зонами [6, 14, 15]. Поэтому, если при оценке степени геоэкологического риска Байкальского региона следовать методике, используемой авторами для платформенных территорий, то можно получить неоднозначные, а, скорее всего, и недостоверные результаты. Необходим новый подход, который позволит оценить степень геоэкологического риска не только на платформенных территориях, но и в орогенных областях, и, в частности, в Байкальском регионе в целом.

Для оценки степени геоэкологического риска ландшафтнотерриториального комплекса (ЛТК) Байкальского региона авторами предлагается использовать следующую математическую модель.

Предположим, что последовательность геоэкологических состояний исследуемой системы ЛТК представляет собой поток однородных событий, который удовлетворяет условиям независимости, однородности и ординарности, т.е. представляет собой так называемый простейший поток. Действительно, учитывая геологический генезис геоэкологических рисков, возникающих на какой-либо территории, в первом приближении вполне можно допустить, что число событий (проявлений опасных геодинамичес-ких процессов незначительных энергетических классов, а именно такие и рассматриваются) в каждом из двух произвольно взятых, одинаковых по длительности и следующих друг за другом временных интервалов [a, b] и [c, d] не зависят друг от друга.

Из той же геологической природы рассматриваемых геоэкологических рисков следует, что вероятность реализации подобных опасностей в течение временного интервала [a, b] совпадает с вероятностью реализации этих опасностей в течение временного интервала [c, d], что, фактически означает соблюдение условия однородности.

Далее, если за один и тот же бесконечно малый промежу- ток времени, т.е. практически одновременно, реализуются две геоэкологические опасности геологической обусловленности, то в геофизическом смысле энергетически они рассматриваются как одно событие, т.е. выполняется и условие ординарности.

Обозначим через P_k(t) вероятность того, что в течение некоторого промежутка времени длительности t к процессу реализации различных геоэкологических состояний рассматриваемой территории будут предъявлены k требований (различных геодинамических процессов). В силу указанных нами выше условий эта вероятность не зависит ни от выбора системы отсчета, ни от предыстории самой системы. Поэтому условия, определяющие простейший поток в приложении к нашей задаче, позволяют однозначно построить формулы для определения вероятностей P_k(t) .

Из теории вероятностей известно, что вероятность P_k(t) при любом k ≥ 0 может быть найдена из соотношения вида:

Pk(t) = aT e '                    (1)k!

Выражение (1) является решением системы дифференциальных уравнений:

P ‘ t ) = ^{-a P} o ⁽ t \                          (2)

_ P/( t) = -aPk (t) + apk-1( t), где α = P’0 (0), , k = 1, 2, … . .

Определим теперь набор геоэкологических состояний для исследуемой территории Байкальского региона.

Состоянием 1 назовем такое состояние системы ЛТК, при котором процессы, генерируемые комплексом геоэкологических опасностей различного происхождения, не переводят систему ЛТК в другое состояние, отличное от состояния 1, т.е. состояние системы флуктуирует около текущего на данный момент времени состояния (система находится в квазиравновесном состоянии).

Состоянием 2 будем называть состояние системы ЛТК, при котором те же самые процессы переводят систему в состояние, после которого возможно либо возвращение к состоянию, имевшемуся до реализации указанных процессов, либо система остается в новом квазиравновесном состоянии, либо переходит в новое состояние, отличное по своим энергетическим характеристикам от квазирав-новесного.

Состоянием 3 назовем состояние системы ЛТК, при котором процессы либо переводят систему в состояние, имевшееся до протекания в ней этих процессов, либо «удерживают» ее в квазиравновесном состоянии.

Чтобы составить систему уравнений для искомых вероятностей P₁(t), P₂(t), P₃(t), соответствующих состояниям 1, 2, 3, необходимо определить интенсивности процессов α _i j и α j _i (где i = 1, 2, 3; j = 1, 2, 3), которые физически представляют собой следующие величины.

Величина α _i j – это сумма энергетических параметров процессов, протекающих в системе, окончание которых приводит к непосредственному переходу системы из состояния i в состояние j , т.е. i —— j .

Величина α j _i – это сумма энергетических параметров, окончание которых приводит систему к непосредственному переходу j —— i .

Построение вероятностной модели

Итак, мы предположили, что P1(t), P2(t), P3(t) – вероятности нахождения системы ЛТК в геоэкологических состояниях 1, 2, 3. В таком случае интенсивности αij и αji будут определяться в соответствии со следующей схемой (рис. 1). Тогда изменения указанных вероятностей с учетом всего выше- изложенного будут описываться следующей системой дифференциальных уравнений:

P ( t ) = " « 12 ^P1⁽ t ) + ^a 21 ^P 2⁽ t ),

’ P ( t ) = a i2 P ( t ) -(a 21 + a 23 ) P 2 ( t ) + а з2 P 3 ( t ),         (3)

P ^ ( t ) = a ₂₃ P ₂ ( t ) - a ₃₂ P ₃ ( t ).

Знак «–» в уравнениях системы (3) указывает на то, что интенсивность, перед которой стоит этот знак, уменьшает вероятность нахождения ЛТК в состоянии i , знак «+» – наоборот, увеличивает вероятность нахождения системы в состоянии i .

Представим систему (3) в виде характеристического уравнения:

- X ³ + BX ² + CX = 0 ,                      (4)

где    B = -(a12 + a 21 + a 32 + a 23),C  a12a 21 - a12(a 32 + a 21 + a 23)-a 21аз2.

Корнями характеристического уравнения (4) являются следующие значения параметра λ :

. n . 5 + 7F + 4C

Л, — U, Az. —.

• 1          -2

. _S-VS²+4C

Найдем компоненты собственных векторов V ₁ , V ₂ , V ₃ , соответствующих значениям параметров λ₁, λ ₂, λ₃ .

Количественное распределение землетрясений по энергетическим классам

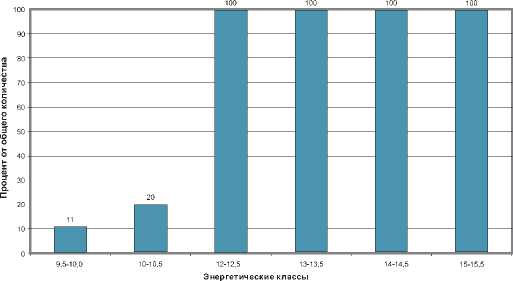
Рис. 5. Количественное распределение землетрясений энергетических классов К = 9,0 ÷ 11,5, попавших в зоны вероятностного проявления геодинамических подвижек относительной количественной энергетической величины 0,1 – 0,4

Количественное распределение землетрясений по энергетическим классам

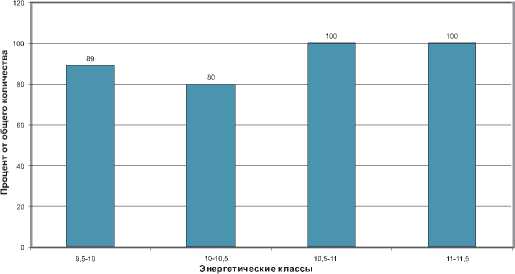
Рис. 6. Количественное распределение землетрясений энергетических классов К = 9,5 ÷ 15,5, попавших в зоны повышенного комплексного геоэкологического риска относительной количественной энергетической величины 0,4 – 0,7

1. Для λ = λ₁ собственный вектор V ₁ :

V1 {а 2га

32; а12а

' 23 j -

2. Для λ = λ ₂ собственный вектор V ₂ :

V2{а21а32; (а12 + Х)а32; (а12 + а21 + а23 + Х2)Х2 + а12а23}. (6)

Далее, предположим, что в некоторый условный начальный (нейтральный) момент времени t = 0 система (ЛТК) находится в состоянии 2, т.е. это событие является достоверным, а события, соответствующие состояниям 1 и 3, являются невозможными, т.е. P₁(t) = P₃(t) = 0; P₂(t) = 1.

Тогда, следуя работе [12], получим соотношения для определения коэффициентов C ₁ , C ₂ и C ₃ :

3.Для λ = λ ₃ собственный вектор V ₃ :

V{а21аз2; (а^ + Х^а32; (а12 + а21 + а23 + Х3)Х3 + а12а23}.(7)

Как показано в работе [12], общее решение исходной системы дифференциальных уравнений представляется в следующем виде:

C —

⁽ a 21 a 33

- a 23 a 31 ⁾⁽ a i2 a 33

_ ^a 13 a 31 ^{- a} 11 a 33

C 2 —               C1 ;

a 12 a 33 ^- a 13 a 32

C3 —--(a 31C1 + a 32 C2).

a 33

a 33 ⁽ a 12 a 33 - a 13 a 32 )

- ai3a32) + (a22a33 - a23a32)(a13a31

; ^a 11 a 33 )

Основные результаты

P₁( t ) — а ₂₁ а ₃₂ C ₁ + а ₂₁ а ₃₂ C ₂ e ^x t + а ₂₁ а ₃₂ C ₃ e ^ t ;

■ P ₂ ( t ) — а ₁₂ а ₃₂ C ₁ + ( а ₁₂ + Х ₂) а ₃₂ C ₂ e ^x + ( а ₁₂ + Х ₃) а ₃₂ C ₃ e ^x ;

Х t

Д( t ) — а 12 а 23 C 1 + [( а 12 + а 21 + а 23 + Х 2 ) Х 2 + а 12 а 23 ] C 2 e ^x 2 + [( а 12 + а 21 + а 23 + Х } ) Х + а^а 23 ] C 3 e -

По рассчитанным таким образом полям данных для всей (8) территории Байкальского региона были построены результативные карты пространственного распределения вероятностей проявления геодинамических подвижек, оползневых и просадочных явлений, а также комплексного геоэкологического риска.

Так, например, на рис. 2 представлена карта-схема пространственно-вероятностного распределения комплек-

Таблица 1. Характеристика землетрясений, произошедших в Байкальском регионе в 2008 г., по зонам геоэкологического риска (по состоянию на 01.09.2008 г.)

№	и я S с и rv В < Н ч & м У к m	Зоны вероятностного проявления геодинамических подвижек				Зоны повышенного комплексного геоэкологического риска		« су S и к К Л и & к S © Н К У g S S < У Й < П5  и 2 <у И S к со  X  Н  су £ ° S у о и и
		Относительная количественная энергетическая характеристика зоны
		0 - 0,1		0,1 - 0,4		0,4 - 0,7
		Кол-во	Доля от общего кол-ва	Кол-во	Доля от общего кол-ва	Кол-во	Доля от общего кол-ва
1.	9,5 – 10,0	25	54%	16	35%	5	11%	46
2.	10,0 – 10,5	5	50%	3	30%	2	20%	10
3.	10,5 – 11,0	3	75%	1	25%	-	-	4
4.	11,0 – 11,5	1	50%	1	50%	-	-	2
5.	12,0 – 12,5	-	-	-	-	1	100%	1
6.	13,0 – 13,5	-	-	-	-	1	100%	1
7.	14,0 – 14,5	-	-	-	-	1	100%	1
8.	15,0 – 15,5	-	-	-	-	1	100%	1

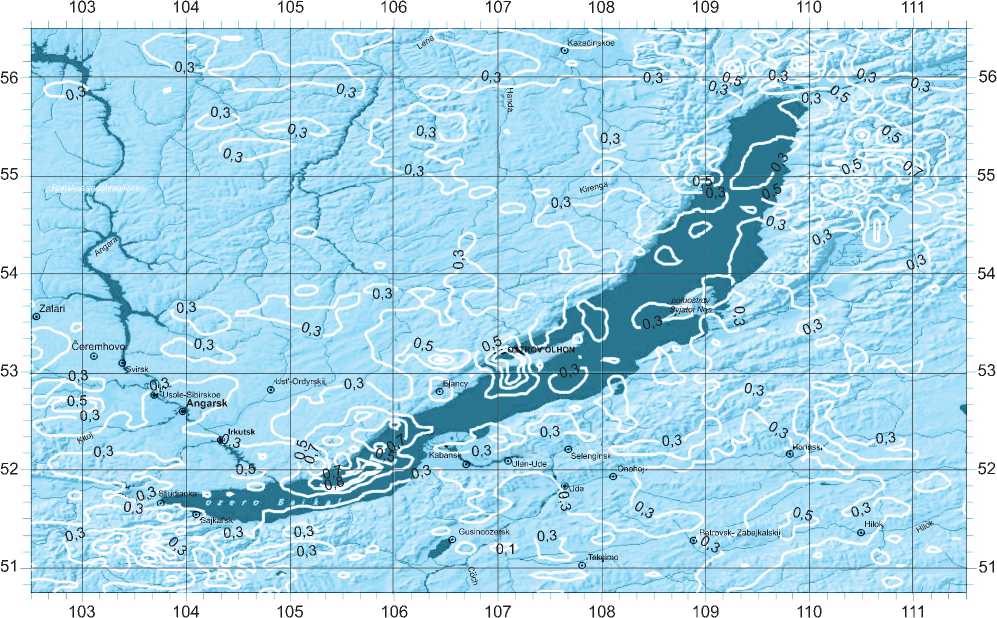
Рис. 2. Карта-схема пространственно-вероятностного распределения комплексного геоэкологического риска для территории Байкальского региона. По горизонтальным осям указана долгота (в градусах), по вертикальным осям – широта (в градусах)

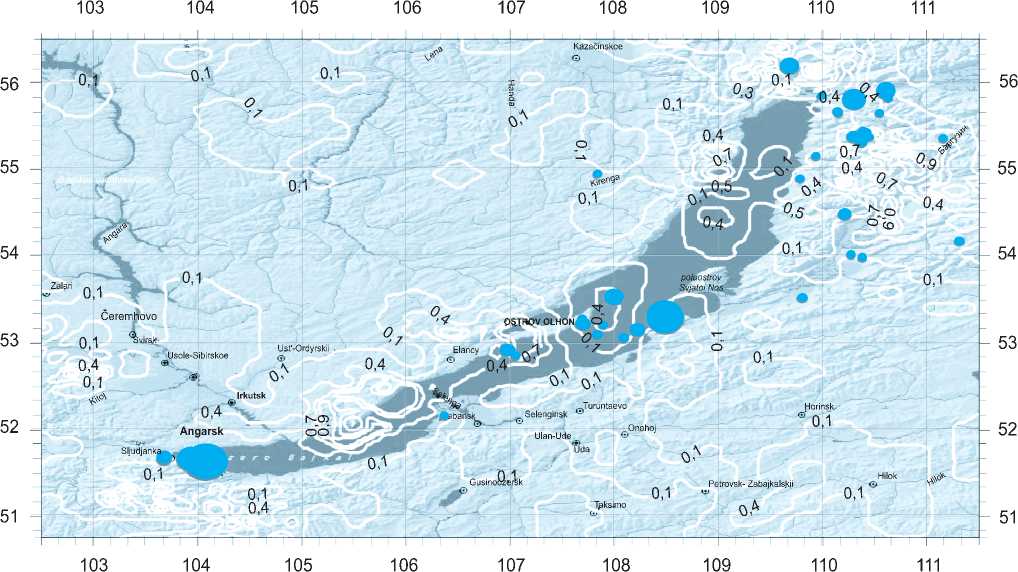
Рис. 3. Карта-схема пространственно-вероятностного распределения геодинамических криповых подвижек для территории Байкальского региона с эпицентрами произошедших в 2008 г. землетрясений (по состоянию на 01.09.2008). По горизонтальным осям указана долгота (в градусах), по вертикальным осям – широта (в градусах)

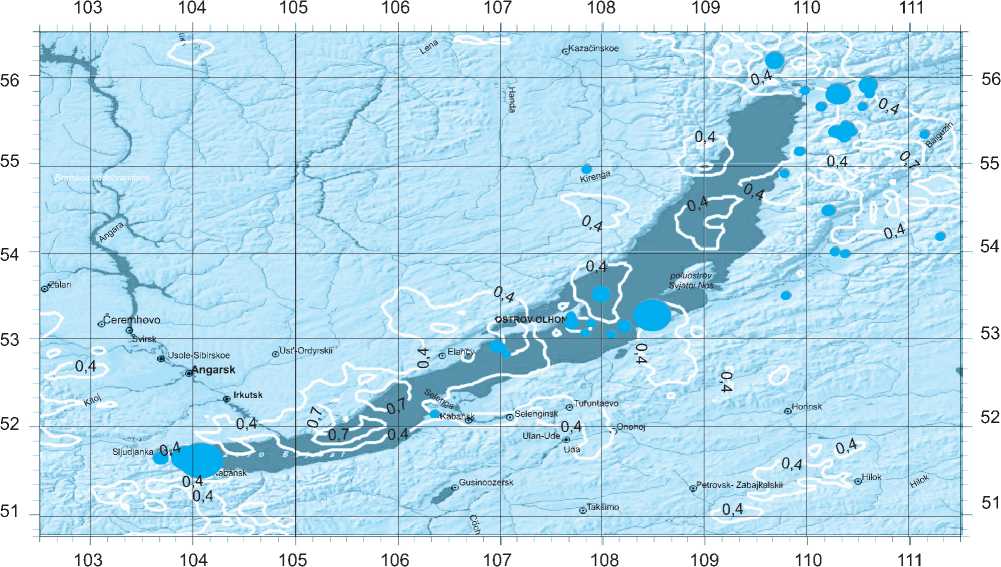
Рис. 4. Карта-схема пространственно-вероятностного распределения комплексного геоэкологического риска для территории Байкальского региона с эпицентрами произошедших в 2008 г. землетрясений (по состоянию на 01.09.2008). По горизонтальным осям указана долгота (в градусах), по вертикальным осям – широта (в градусах)

сного геоэкологического риска для территории Байкальского региона.

На представленной карте-схеме изолинии вероятностей построены с неравномерным шагом значений. Это обусловлено необходимостью сделать карту-схему одновременно и информативной, и наглядной, и удобно читаемой. Что же касается диапазонов значений вероятностей и сопоставляемой с ними степенью риска, то здесь необходимо отметить следующее.

Области, оконтуренные изолиниями со значением вероятности 0,3, полагаем считать зонами латентно-потенциального риска; изолиниями со значением 0,5 – зонами умеренного риска; 0,7 – зонами повышенного риска; 0,8 – зонами чрезвычайной опасности ( рис. 2 ). Такая градация диапазонов значений вероятности и сопоставимой с ними степенью риска является условно-общей, и при оценке опасности для различных объектов, скажем, для атомных станций, туристско-рекреационных комплексов или лесных массивов, она должна существенно варьировать по степени тяжести.

Также авторами была выполнена оценка количественного распределения землетрясений, произошедших в Байкальском регионе в 2008 г. (по состоянию на 01.09.2008 г.) по зонам геоэкологического риска ( табл. 1, рис. 3 – 6 ).

Заключение

Итак, рассмотренный нами подход, основанный на представлении возможных геоэкологических состояний ландшафтно-территориального комплекса как простейшего потока событий с последующим построением математической модели, позволяет оценивать пространственно-вероятностные распределения опасностей, исходящих от геологической составляющей окружающей среды.

Анализ результатов исследований, представленных в табл. 1 и на рис. 3 – 6 , позволяет сделать следующие важные выводы.

• 1.    Для прогнозирования пространственного распределения возможных землетрясений энергетических классов 9,0 – 11,5, т.е. с магнитудой от 2,5 до 4,0 в орогенных областях наиболее оптимальным является выполнение таких оценок на основе выявления зон возможных геодинамических криповых подвижек; величина относительной количественной энергетической характеристики таких зон при этом должна принадлежать диапазону от 0,1 до 0,4.

• 2.    Прогнозирование пространственного распределения возможных крупных сейсмических событий, таких, как тектонические землетрясения энергетических классов

  
  
  

• 3.    При этом наибольшее внимание следует обращать на те участки оцениваемой территории, где наиболее высока градиентность вертикальных и горизонтальных смещений, возникающих в геологической среде верхних частей

12,0 – 15,0 и выше (т.е. с магнитудой от 5,0 и выше), на наш взгляд, необходимо производить на основе выявления зон повышенного комплексного геоэкологического риска, т.е. такого геоэкологического риска, в котором структурно учитывается не только вероятности возникновения геодинамических криповых подвижек, но и проявления таких опасных экзогенных процессов, как карст, проседания, оползни, обвалы.

земной коры. Количественно такие зоны повышенного комплексного геоэкологического риска, по результатам выполненных исследований, следует оценивать в относительных количественных энергетических единицах как величину, принадлежащую интервалу от 0,4 до 0,7.

Авторы также полагают, что в подобный подход в методическом плане для орогенных областей является достаточно действенным, и при его дальнейшем применении к ряду других подобных областей позволит выработать единую эффективную методику вероятностного прогнозирования пространственно-временного распределения сейсмических событий различных энергетических классов■