Моделирование гибкости нанокомпозитных трубопроводов

O ne of the main problems in maintaining the operability of technological pipeline systems is the corrosion of steel pipes. The most promising solution to this problem is the transition to non-metallic pipelines, for example, composite systems [1, 2, 3]. Currently, more than 200 thousand tons of pipes from composite materials (CM) are produced in the world [4]. Fiberglass pipes [5, 6, 7] are widely used, made on horizontal and radial cross winding machines using wet impregnation of glass-filled fiber with an epoxy binder [8].

The most common is the manufacture of composite pipes by the method of continuous winding of glass fiber on a stepwise moving mandrel [9] – the so-called «walking» mandrel. One of the available machine options is the regulation of the direction of glass-laying on the surface of the mandrel [10]. The winding path is determined by the angle of reinforcement φ. It is the angle between the direction of glass roving laying and the pipeline axis that largely determines the main characteristics of the strength and reliability of the composite pipe [11].

MAIN PART

The relevance of the task

The use of composite pipelines with a curved axis of laying is accompanied by the most complex technological strength modes. During their production, an inhomogeneous structure is formed with variable reinforcement angles φ (the angle between the tangent to the reinforcement path and the axial direction of the pipe). Pipeline zones in the area of rotation angles, as a rule, experience the greatest longitudinal and ring forces. With sufficient flexibility of the material, the probability of the manifestation of the Karman effect (flattening of the cross section during bending) is highest [12, 13]. The authors of [14] showed that the quality of installation and further operation of a composite pipe under variable temperature conditions largely depends on its rigidity. Increasing the flexibility of the pipe will ensure the reliability and durability of the pipeline system, even under conditions of accidental shock loads [15].

The work is devoted to modeling the coefficient of change in the flexibility of the pipeline depending on

Table 1

Initial values for the coefficient of increase in pipe flexibility k

№	Reinforcement angle, φ, o	Bend angle, Ф, o	Flexibility factor, k , r.u.
	Х 1	Х 2	Y
1	55	180	1.39
2	65	180	1.27
3	75	180	1.23
4	85	180	1.21
5	0	180	2.97
6	55	135	1.36
7	65	135	1.26
8	75	135	1.22
9	85	135	1.20
10	0	135	2.91
11	55	90	1.30
12	65	90	1.22
13	75	90	1.19
14	85	90	1.17
15	0	90	2.67
16	55	45	1.19
17	65	45	1.17
18	75	45	1.16
19	85	45	1.16
20	0	45	2.08

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

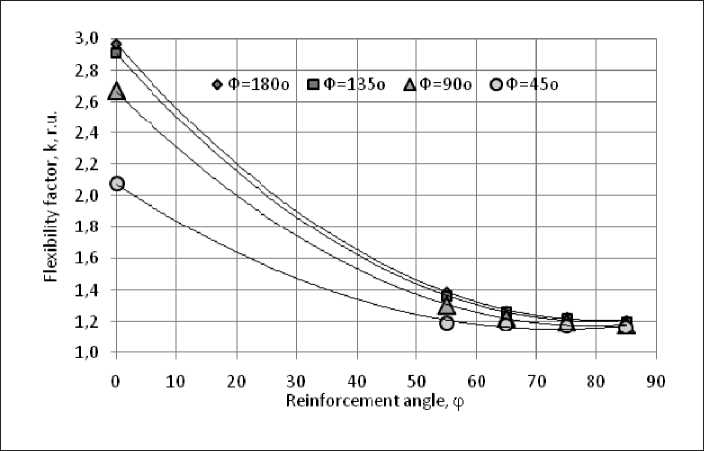
Fig. 1. The relationship of the coefficient of change in the flexibility of the KM pipe with reinforcement angles φ and bending Ф of the pipeline

the bending angles of its axis Ф and the angle of reinforcement φ [16]. The object of modeling is a pivotally supported curvilinear pipe made of Kevlar 49/PR-286 composite material with a diameter of 167 mm and a wall thickness h = 4.2 mm. The number of layers is 6 [17].

Initial data for model development

The initial data for modeling the behavior of the coefficient of change in flexibility k were the results of the finite element method [18, 19] for calculating the strength characteristics of a curved pipe made of Kevlar-286 composite material (Table 1, Fig. 1).

An analysis of the source data showed that in the full range of variation of the reinforcement angle φ from 0о to 85о, the studied dependence is non-linearly monotonically decreasing for any curvature of the pipeline F.

Settlement part

Depending on the range of values of the angle of reinforcement φ, we selected modeling methods.

Modeling in the range of φ∈[55о; 85о]

In the range of reinforcement angles from 55о to 85о, the dynamics of the coefficient of increase in pipe flexibility is almost linear (the average deviation does not exceed 5%). In addition, glass roving winding machines, used in practice, provide reinforcement angles in precisely this range [20]. This allows you to use a technically un- complicated method for developing a multi-parameter linear regression model.

The main goal of multiple regression is to build a model with a large number of factors, while determining their combined effect on the modeled indicator. The implementation of the method in matrix form involves several consecutive steps.

Step 1. Formation of source data matrices for modeling:

X – matrix of influencing parameters – φ and Ф – taking into account the accepted number of influencing parameters.

Y is the matrix of the desired function k is the coefficient of variation of the flexibility of the composite pipeline.

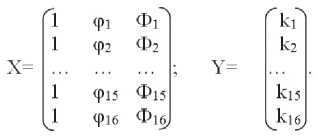
Matrices are formed on the basis of the initial data of Table 1.

Step 2. Formation of the transposed matrix Хт.

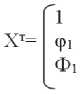
i ... i i "

ф2 ... ф15  ф16

Фг ... Ф15 Ф16

Step 3. After a series of transformations of the original matrices, a vector of estimates of the coefficients of the regression equation is obtained:

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

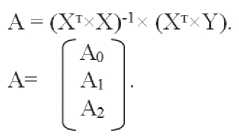
Range modeling at φ∈[55о; 85о]

Expanding the range of variation of reinforcement angles in the manufacture of composite pipelines is a very promising direction. At φ → 0^о, the coefficient of flexibility of the pipe increases significantly, which helps to increase the reliability and performance of a curved composite pipe [21]. To take into account the nonlinearity of the relationship between the coefficient of change in the flexibility of the pipeline with φ and Ф, the transition to asymptotic variables seems optimal [22]. The authors of [22] showed that asymptotic variables can reliably develop a model of a function that is characterized by a tendency to some asymptotes at the boundaries of the considered range of values.

To pass to asymptotic variables, use the model function:

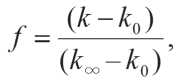
where k0 = k(Ф) at φ = φmin = 0о, k∞ = k(Ф) at φ = φmax = 85о, for which φmin и φmax defined in Table 1. One-parameter regression equations fork0 and k∞ set by least squares method.

The main property of the model function f is that for any values of the angle of curvature Ф f = 0 at φ = φ_min, and f = 1 at φ = φ_max.

The regression equation for f is established by its values by numerical simulation at values of the reinforcement angle φ in the rangefrom 0о to 85о.

Analysis of the resultsRange simulation results at φ∈[55о; 85о]

As a result of the implementation of the matrix method for finding the coefficients in the multiple linear regression equation, the components of the vector of estimates of the coefficients of the equation were determined (table 2).

The result of the implementation of the multiple regression method under the condition φ ∈ [55^о; 85^о], the type of dependence of the coefficient of flexibility of the pipeline depending on the angle of reinforcement

Table 2

Coefficients of the linear equation of multiple regression to determine the coefficient of change in the flexibility of the composite pipeline

№	Influence factor in the equation	Coefficient designation	The value of the coefficient of the regression equation
1	Free ratio	А 0	1.426
2	Reinforcement angle	А 1	–0.00405
3	Pipeline angle of curvature	А 2	0.000789

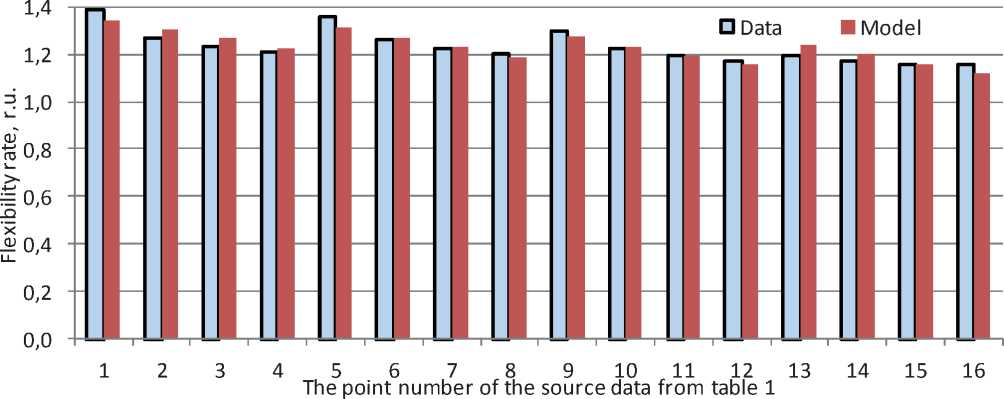
Fig. 2. Assessment of the reliability of the simulation results of the range φ ∈ [55^o; 85^o]

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

φ and the angle of curvature of the axis of the pipeline Ф was established:

k (φ, Ф) = 1,426–0,00405×φ+0,000789×Ф.

The adequacy of the obtained results was assessed by comparing the initial data of the values of the coefficient of flexibility increase of the composite pipeline with model values (Fig. 2).

A quantitative assessment of the quality of the resulting multiple regression equation showed that the modeling error at the points of the source data varies from 0,2% to 4%, averaging 1,9% for the sample.

Range simulation results at φ∈[0о; 85о]

As shown in [22], the efficient use of asymptotic coordinates is possible for functions of a certain type. In particular, the direct application of asymptotic coordinates is inadmissible if F → ∞ is at least on one edge of the interval under study. In our case, k → ∞ for φ → 0 (Fig. 1).

This situation, according to the recommendations of the authors [23], is allowed by the transformation of the initial data of the form:

к = 1/ k.

The conversion results are given in Table 3.

The stages of the sequential implementation of the transition of the original function to asymptotic coordinates are shown in Fig. 3.

Taking into account the obtained analytical expression for the model function f, the dependence of the coefficient of increase in the flexibility of the composite pipe on the reinforcement angle φ and the pipe curvature angle Ф was identified:

k(φ, Ф) = 0,777Ф0,265[(0,002+0,0218φ–0,00012φ2)× ×(0,757Ф0,233–1)+1]–1, where φ,o – composite pipe reinforcement angle;

Ф,o – pipeline axis curvature.

Table 3

Initial values for the coefficient of increase in pipe flexibility in converted format, к

к	Ф = 180о	Ф = 135о	Ф = 90о	Ф = 45о
φ = 0o	0.337	0.344	0.375	0.481
φ = 55o	0.719	0.735	0.769	0.840
φ = 65o	0.787	0.794	0.820	0.847
φ = 75o	0.813	0.820	0.840	0.855
φ = 85o	0.826	0.833	0.855	0.862

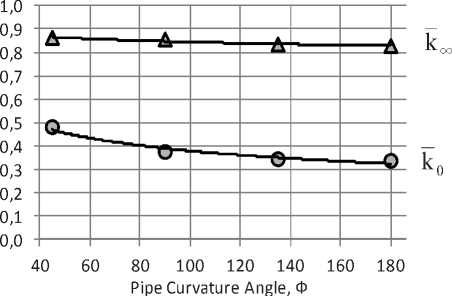
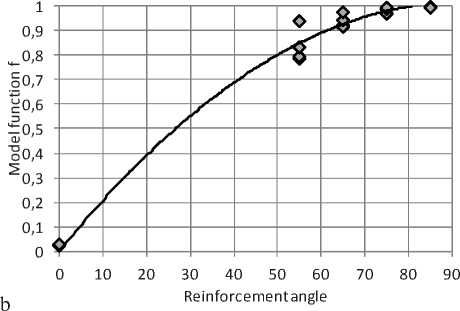
Fig. 3. Stages of the implementation of the asymptotic coordinate method: а – boundary functions k₀ and k _∞ ; b – model function

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

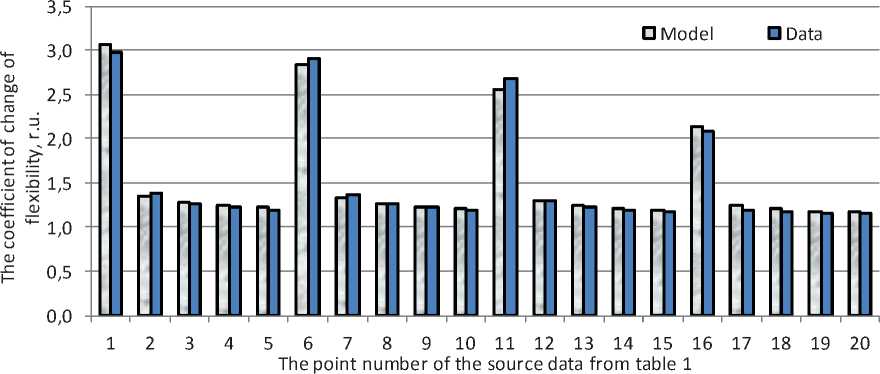
Fig. 4. Assessment of the reliability of the simulation results φ ∈ [0^o; 85^o]

The adequacy of the obtained results was assessed by comparing the initial data of the values of the coefficient of flexibility increase of the composite pipeline with model values (Fig. 4).

A quantitative assessment of the adequacy of the obtained multiple regression equation showed that the modeling error at the points of the source data varies from 0.2% to 5%, averaging 2% on the sample.

CONCLUSION

• 1.    It is shown that an increase in the flexibility of the composite pipeline contributes to ease of installation and increases the reliability of the operation of the oil pipeline system.

• 2.    It was found that the flexibility of the KM pipe increases with decreasing reinforcement angle. With a decrease in the angle of reinforcement from 85^o to 55^o, the dynamics of the coefficient of flexibility increase is almost linear. With a further decrease in the angle of reinforcement up to 0^o, the intensity of the increase in the flexibility coefficient of the composite pipe gradually increases.

• 3.    Developed regression equations to determine the coefficient of increase in the flexibility of the KM pipe depending on the angle of reinforcement and the angle of curvature of the pipeline: Non-linear model for φ ∈ [0^o; 85^o] and the linear model for φ ∈ [55^o; 85^o]. The average error of the models does not exceed 2%.

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

ВВЕДЕНИЕ

О дной из основных проблем поддержания работоспособности технологических трубопроводных систем является коррозия стальных труб. Наиболее перспективным решением этой проблемы представляется переход на неметаллические трубопроводы, например, композитные системы [1, 2, 3]. В настоящее время в мире производится более 200 тысяч тонн труб из композитных материалов (КМ) [4]. Широко применяются стеклопластиковые трубы [5, 6, 7], изготовленные на станках горизонтальной и радиально-перекрестной намотки по технологии мокрой пропитки стеклонаполненного волокна эпоксидным связующим [8].

Наиболее распространено изготовление композитных труб способом непрерывной намотки стекловолокна на ступенчато движущуюся оправку [9] – так называемая «шагающая» оправка. Одной из доступных опций станков является регулирование направления укладки стеклоровинга на поверхности оправки [10]. Траектория намотки определяется углом армирования φ. Именно угол между направлением укладки стеклоровинга и осью трубопровода во многом определяет основные характеристики прочности и надежности композитной трубы [11].

ОСНОВНАЯ ЧАСТЬ

Актуальность задачи

Использование композитных трубопроводов с криволинейной осью укладки сопровождается наиболее сложными технологическими прочностными режимами. При их производстве формируется неоднородная структура с переменными углами армирования φ (угол между касательной траектории армирования и осевым направлением трубы). Зоны трубопроводов в области углов поворота, как правило, испытывают наибольшие продольные и кольцевые напряжения. При достаточной гибкости материала вероятность проявления эффекта Кармана (сплющивания поперечного сечения при изгибе) наиболее высока [12, 13]. Авторами [14] показано,

Таблица 1

Исходные значения коэффициента увеличения гибкости трубы k

№ п/п	Угол армирования, φ, о	Угол изгиба оси, Ф, о	Коэффициент увеличения гибкости, k , о.е.
	Х 1	Х 2	Y
1	55	180	1,39
2	65	180	1,27
3	75	180	1,23
4	85	180	1,21
5	0	180	2,97
6	55	135	1,36
7	65	135	1,26
8	75	135	1,22
9	85	135	1,20
10	0	135	2,91
11	55	90	1,30
12	65	90	1,22
13	75	90	1,19
14	85	90	1,17
15	0	90	2,67
16	55	45	1,19
17	65	45	1,17
18	75	45	1,16
19	85	45	1,16
20	0	45	2,08

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

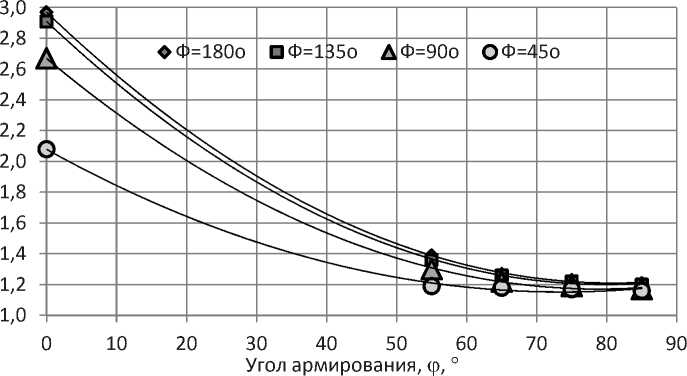
Рис.1. Взаимосвязь коэффициента изменения гибкости КМ-трубы с углами армирования φ и изгиба Ф трубопровода

что качество монтажа и дальнейшей эксплуатации композитной трубы в переменных температурных условиях во многом зависит от ее жесткости. Повышение гибкости трубы позволит обеспечить надежность и долговечность трубопроводной системы даже в условиях случайных ударных нагрузок [15].

Работа посвящена моделированию коэффициента изменения гибкости трубопровода в зависимости от углов изгиба его оси Ф и угла армирования φ [16]. Объектом моделирования является шарнирно-опертый криволинейный трубопровод из композитного материала Kevlar49/PR-286 диаметром 167 мм и толщиной стенки h = 4,2 мм. Количество слоев – 6 [17].

Исходные данные для разработки модели

Исходными данными для моделирования поведения коэффициента изменения гибкости k послужили результаты реализации метода конечных элементов [18, 19] для расчета характеристик прочности криволинейного трубопровода из композитного материала Kevlar49/PR-286 (табл. 1, рис. 1).

Анализ исходных данных показал, что в полном диапазоне изменения угла армирования φ от 0о до 85о изучаемая зависимость является нелинейной монотонно убывающей для любой кривизны трубопровода Ф.

Расчетная часть

В зависимости от диапазона значений угла армирования φ нами были подобраны методы моделирования.

Моделирование в диапазоне φ∈[55о; 85о]

В диапазоне значений углов армирования от 55о до 85одинамика коэффициента увеличения гибкости трубы является практически линейной (среднее отклонение не превышает 5%). Кроме того, применяемые на практике машины намотки стекло-ровинга обеспечивают углы армирования именно в таком диапазоне [20]. Это позволяет использовать несложный технический метод разработки многопараметрической линейной регрессионной модели.

Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом совокупное их воздействие на моделируемый показатель. Реализация метода в матричном виде подразумевает несколько последовательных шагов.

Шаг 1. Формирование матриц исходных данных для моделирования:

Х – матрица влияющих параметров –φ и Ф – с учетом принятого количества влияющих параметров.

Y – матрица искомой функции k – коэффициента изменения гибкости композитного трубопровода.

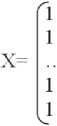
ф1 фГ ф2 Фг ф15 Ф15

ф16 ф|6

^кГ к2

кк5

<_ki6

Матрицы сформированы на основе исходных данных табл. 1.

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

Шаг 2. Формирование транспонированной матрицы Хт.

"1

Ф1

Ф1

1 ... 1       1

ф2 ... ф15 ф1б

Ф2 ... Ф]5 Ф16

Шаг 3. После ряда преобразований исходных матриц получен вектор оценок коэффициентов уравнения регрессии:

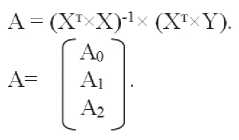
Моделирование в диапазоне φ∈[0о; 85о]

Расширение диапазона вариации углов армирования при изготовлении композитных трубопроводов является весьма перспективным направлением. При φ → 0о коэффициент гибкости трубы значительно возрастает, что способствует повышению надежности и работоспособности криволинейной композитной трубы [21]. Для учета нелинейности функции взаимосвязи коэффициента изменения гибкости трубопровода с φ и Ф оптимальным представляется переход к асимптотическим переменным [22]. Авторами [22] показано, что асимптотические переменные позволяют достоверно разрабатывать модель функции, которая характеризуется стремлением к некоторым асимптотам на границах рассматриваемого диапазона значений.

Для перехода к асимптотическим переменным используют модельную функцию:

где k0 = k(Ф) при φ = φmin = 0о, k∞ = k(Ф) при φ = φmax = 85о, для которых φmin и φmax определены по табл. 1. Однопараметрические уравнения регрессии для k0 и k∞ установлены методом наименьших квадратов.

Главное свойство модельной функции f состоит в том, что при любых значениях угла кривизны Ф f = 0 при φ = φ_min, и f = 1 при φ = φ_max.

Таблица 2

Коэффициенты линейного уравнения множественной регрессии для определения коэффициента изменения гибкости композитного трубопровода

№ п/п	Влияющий фактор в уравнении	Обозначение коэффициента	Значение коэффициента уравнения регрессии
1	Свободный коэффициент	А 0	1,426
2	Угол армирования	А 1	–0,00405
3	Угол кривизны трубопровода	А 2	0,000789

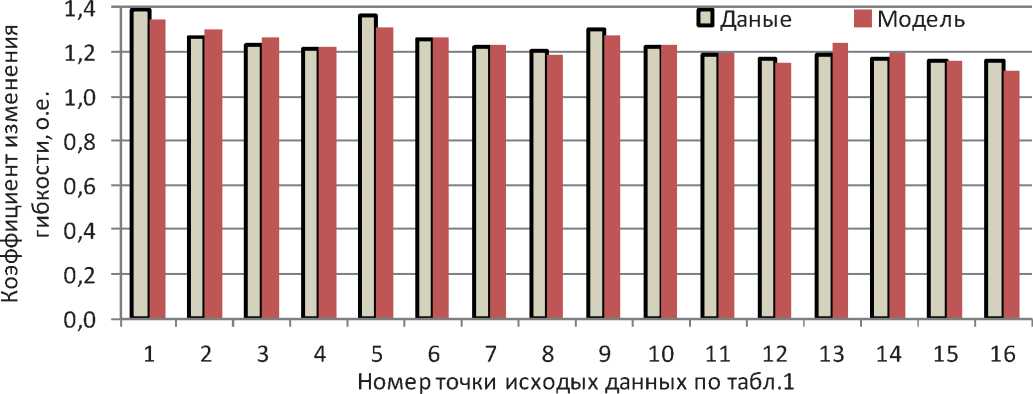
Рис. 2. Оценка достоверности результатов моделирования в диапазоне φ ∈ [55^о; 85^о]

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

Уравнение регрессии для функции f устанавливают по ее значениям численным моделированием при значениях угла армирования φ в диапазоне от 0о до 85о.

Анализ полученных результатовРезультаты моделирования в диапазоне φ∈[55о; 85о]

В результате реализации матричного способа нахождения коэффициентов в уравнении множественной линейной регрессии были определены компоненты вектора оценок коэффициентов уравнения (табл. 2).

В результате реализации метода множественной регрессии при условии φ ∈ [55^о; 85^о] был установлен вид зависимости коэффициента изменения гибкости трубопровода в зависимости от угла армирования φ и угла кривизны оси трубопровода Ф:

k (φ, Ф) = 1,426–0,00405×φ+0,000789×Ф.

Оценка адекватности полученных результатов выполнена сравнением исходных данных значений коэффициента увеличения гибкости композитного трубопровода с модельными величинами (рис. 2).

Количественная оценка качества полученного уравнения множественной регрессии показала, что ошибка моделирования по точкам исходных данных изменяется от 0,2% до 4%, составляя в среднем по выборке 1,9%.

Результаты моделирования в диапазоне φ∈[0о; 85о]

Как показано в [22], эффективное использование асимптотических координат возможно для функций определенного типа. В частности, недопустимо прямое применение асимптотических координат, если F → ∞ хотя бы на одном краю исследуемого интервала. В нашем случае k → ∞ при φ → 0.

Эта ситуация по рекомендациям авторов [23] разрешается преобразованием исходных данных вида:

к = 1/ k.

Результаты преобразования приведены в табл. 3.

Таблица 3

Исходные значения коэффициента увеличения гибкости трубы в преобразованном формате, к

к	Ф = 180о	Ф = 135о	Ф = 90о	Ф = 45о
φ = 0o	0,337	0,344	0,375	0,481
φ = 55o	0,719	0,735	0,769	0,840
φ = 65o	0,787	0,794	0,820	0,847
φ = 75o	0,813	0,820	0,840	0,855
φ = 85o	0,826	0,833	0,855	0,862

а

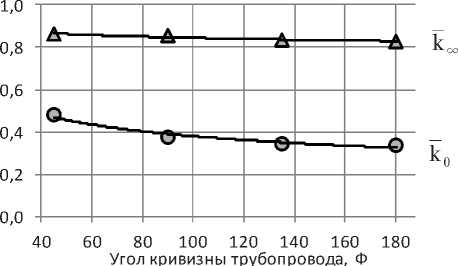
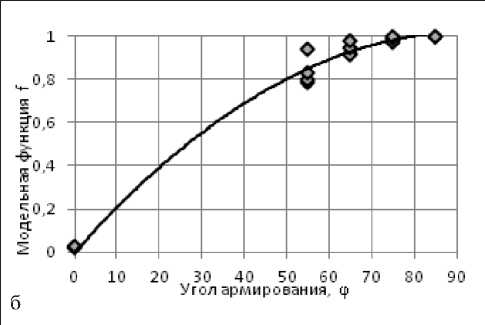
Рис. 3. Этапы реализации метода асимптотических координат: а – граничные функции k₀ и k _∞ ; б – модельная функция

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ

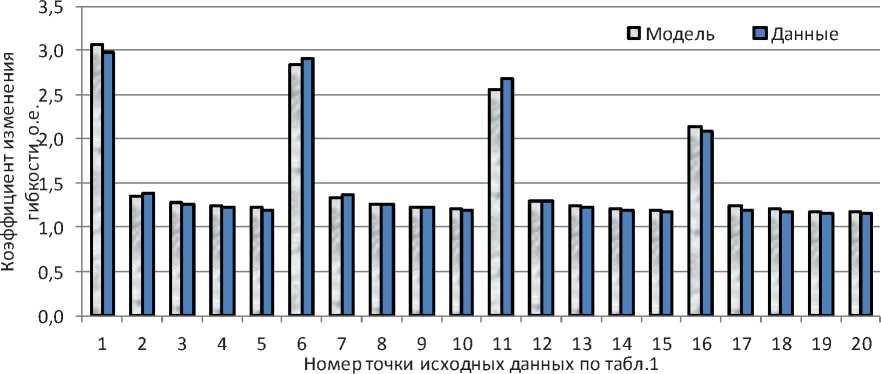
Рис. 4. Оценка достоверности результатов моделирования в диапазоне φ ∈ [0^o; 85^o]

Этапы последовательной реализации перехода исходной функции к асимптотическим координатам показаны на рис. 3.

С учетом полученного аналитического выражения для модельной функции f была идентифицирована зависимость коэффициента увеличения гибкости композитной трубы от угла армирования φ и угла кривизны трубы Ф:

k(φ, Ф) = 0,777Ф0,265[(0,002+0,0218φ–0,00012φ2)× ×(0,757Ф0,233–1)+1]–1, где φо – угол армирования композитного трубопровода;

Фо – угол кривизны оси трубопровода.

Оценка адекватности полученных результатов выполнена сравнением исходных данных значений коэффициента увеличения гибкости композитного трубопровода с модельными величинами (рис. 4).

Количественная оценка адекватности полученного уравнения множественной регрессии показала, что ошибка моделирования по точкам исходных данных изменяется от 0,2 до 5%, составляя в среднем по выборке 2%.

ЗАКЛЮЧЕНИЕ

• 1.    Показано, что увеличение гибкости композитного трубопровода способствует удобству монтажа и повышению надежности эксплуатации нефтепроводной системы.

• 2.    Установлено, что гибкость КМ-трубы возрастает с уменьшением угла армирования. При снижении угла армирования от 85^о до 55^о динамика коэффициента увеличения гибкости практически линейна. При дальнейшем снижении угла армирования вплоть до 0^о интенсивность увеличения коэффициента гибкости композитной трубы постепенно возрастает.

• 3.    Разработаны уравнения регрессии для определения коэффициента увеличения гибкости КМ-трубы в зависимости от угла армирования и угла кривизны трубопровода: нелинейная модель для φ ∈ [0^о; 85^о] и линейная модель для φ ∈ [55^о; 85^о]. В среднем, ошибка моделей не превышает 2%.

RESEARCH OF NANOMATERIALS PROPERTIES • ИССЛЕДОВАНИЕ СВОЙСТВ НАНОМАТЕРИАЛОВ