Моделирование гибридной системы, состоящей из фотоэлектрического преобразователя солнечной энергии и водонагревательного устройства

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 621.382.8                                       

Гибридные системы, представляющие собой комбинацию фотоэлектрических и тепловых устройств преобразования солнечной энергии, были часто на пике внимания в последние годы. Предлагалось множество вариантов таких систем. Довольно эффективная система представляет собой комбинацию фотоэлектрического преобразователя солнечной энергии и коллектора для подогрева воды. Сравнение с общеизвестными нагревательными устройствами для воды, эта гибридная система обладает рядом преимуществ, среди которых меньшие габариты, более низкая рабочая температура теплоносителя, значительное повышение КПД системы, причем здесь одновременно происходит выработка электроэнергии и подогрев воды для отопления. Если же провести сравнение с другими системами, комбинирующими фотоэлектрический модуль и устройство для подогрева воды, то данная система обладает более простой конструкцией, что значительно снижает производственные затраты и поддержание системы в рабочем состоянии. Рабочие характеристики подобной гибридной системы изучались экспериментально [1–3], были проведены исследования численными методами [4–6], однако, все предложенные исследования были посвящены анализу работы системы в стационарном случае. Необходимость такого подхода была обусловлена тем, что работа системы сильно зависит от погодных условий, что приводило к тому, что работа системы рассматривалась пошагово, для разных погодных условий, и каждый шаг был стационарен.

Однако, надо понимать, что работа такой гибридной системы — фотоэлектрический модуль и водонагревающий коллектор — это работа динамической системы. Необходимо постоянно учитывать, что внешние факторы, такие как солнечная энергия и ветры, это факторы постоянно изменяющиеся. Даже работа частей конструкции, таких как циркуляционные насосы, из-за внешних факторов постоянно изменяется. Моделирование динамических систем — это очень затратный, с точки зрения использования машинного времени, подход. Однако при современном развитии информационных технологий эта проблема решается довольно успешно.

В работах [7–9] показано, что разбиение процесса работы гибридной установки на участки стационарного режима, часто не дают даже приблизительных результатов, если внешние факторы – солнечное освещение, дующие в данной местности ветры — быстро меняются. Это, в первую очередь, обусловлено значительной инертностью фотоэлектрического модуля — его время отклика на изменение внешних условий становится довольно значительным. Время отклика фотоэлектрического модуля, как дают оценки, находится в пределах одной минуты, что довольно много для быстро изменяющихся внешних условий [10–12].

Всеобъемлющий анализ теплового режима работы отдельных компонентов гибридной системы, постоянный контроль системы управления гибридного комплекса — это то, что в первую очередь требует динамической модели.

В работах [13–15] рассмотрены несколько численных моделей динамического характера, причем одна из них представляет собой трехмерную модель. Модель позволяет сделать довольно точную оценку выходной тепловой мощности гибрида — фотоэлектрического преобразователя и теплового устройства нагрева воды. Конструкция съема тепла основывалась на однотрубной змеевидной системе. Предложенная трехмерная модель оказалась невероятно громоздкой, что привело к большим затратам машинного времени на обработку результатов моделирования. Так на час работы гибридной системы в реальном режиме требовалось не меньше трех часов работы трехмерной модели. Это привело к тому, что предложенная модель не нашла практического применения.

Целью данной статьи является рассмотрение динамической тепловой модели гибридной системы — фотоэлектрический преобразователь и устройство нагрева воды, которая может быть применима для практического анализа подобной гибридной системы. Предлагаемая модель позволяет проводить оценку мгновенных характеристик гибридной системы, определять в любой момент времени производительность системы, состояние ее компонентов и, в конечном счете, при определенных условиях осуществлять всеобъемлющий тепловой расчет гибридной системы.

Математическая модель гибридной системы — фотоэлектрический преобразователь солнечной энергии + водонагревательное устройство

Передняя часть гибридной системы на основе фотоэлектрического преобразователя энергии и водонагревателя, также поперечное сечение одной трубы с водой, размещенной между двумя средними частями пластин поглотителя показаны на Рисунке. На Рисунке видно, что фронтальная крышка из стекла и фотоэлектрическая пластина разделены воздушным зазором.

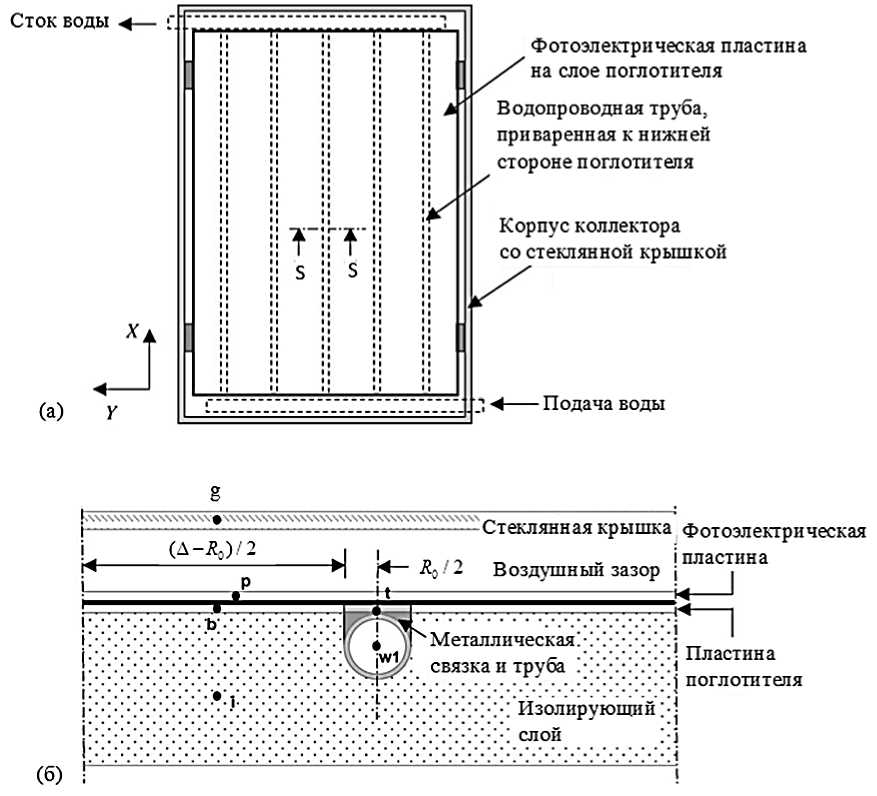
Рисунок. Гибридная система на основе фотоэлектрического преобразователя энергии и водонагревателя

Фотоэлектрическая пластина крепится к адсорбирующей пластине с помощью тонкого слоя клея, который практически не поглощает тепло. При этом адсорбирующие пластины образуют ребра водяных труб, формирующих теплообменник. Ребра теплообменника расположены на равных расстояниях друг от друга вдоль всей панели.

Адсорбирующая пластина и водяные трубы жестко скреплены с помощью сварки. Два общих коллектора, расположенные на двух концах — вверху и снизу — обеспечивают сбалансированный поток воды во всех трубах и, как следствие, среднее расстояние между трубами таково, что практически полностью отсутствует переток тепла от одной трубы к другой. Края и нижняя поверхность панели хорошо теплоизолированы. Компактность и тонкость конструкции панели приводит к потерям поглощенной солнечной энергии в окружающую среду в основном через переднюю и заднюю поверхности панели, причем потери по краям совсем незначительны, особенно для панелей больших размеров.

Анализ гибридной системы в динамическом режиме обычно осуществляется посредством решения равновесных уравнений для переходной энергии для различных компонентов гибридной системы. При использовании метода конечных разностей рассматриваемый объем [16–18] создается посредством задания условных границ, ограничивающих реальное пространство, в котором действуют законы сохранения физики (в частности, баланса массы и энергии). Эта рассматриваемая область представляет собой узел в моделируемой сети. Для данной гибридной системы важным исходным условием является предположение о достаточной однородности свойств материала и физических размеров в каждой составляющей части панели. Такие характеристики, как расход воды и температурный режим во всех параллельных трубках, обычно рассматривают как одинаковые. Общая тепловая картина всей совокупности труб выводится из анализа теплопередачи в непосредственной близости от одиночной водопроводной трубы, как в разрезе S–S на Рисунке (б).

В случае небольшой области размещения труб потери на краях области могут быть поглощены потерями за счет подобранной областью размещения труб. Собирательный теплообмен, направленный вдоль течения воды (направление X) создает градиент со знаком плюс для температуры во всех частях гибридной системы. Данный температурный градиент рассматривают независимо от изменения температуры в поперечном направлении (направление Y). Из сказанного следует, что энергетический обмен между различными частями гибридной системы можно рассматривать, учитывая их средние температуры.

Описанная выше гибридная система может быть разбита на семь блоков, а математически ее можно представить с помощью системы уравнений в матричном виде, описывающих балансы массового расхода и энергии на данный мгновенный момент времени в каждом из рассматриваемых блоков. Первый блок обозначен на Рисунке (б) буквой g, и он представляет собой стеклянную крышку. Второй блок p – это фотоэлектрический блок. Блок номер три, обозначенный буквой b, ограничивает область расположения тонкой поглощающей пластины. Следующие области t — область соединения из металла между пластиной и трубкой, i —слой изоляции, а w1 — вода, текущая в трубе. Один блок, обозначенный w2, не показан на Рисунке. Этот блок ограничивает область выходящей воды.

Из данного блока исходит информация о состоянии выходящей воды, которая поступает в блок, расположенный ниже по течению, что позволяет более точно проводить анализ задержек в передаче энергии и массы. Причины потери энергии при отражении от стеклянной крышки имеют, по крайней мере, два объяснения. Для стеклянной крышки значения его коэффициентов пропускания α , отражения β и коэффициента поглощения τ , который необходимо учитывать как при отражении, так и поглощении, рассчитываются с помощью методов прокладки путей прохождения лучей [19–21].

Обозначим поток солнечной энергии, падающий на поверхность стеклянной крышки через Ф. Энергия солнечного излучения, поглощаемая поверхностью стекла ежесекундно, определяется следующим соотношением:

W c =Фт _с =Ф (1 - a a ).

здесь а — коэффициент пропускания стеклянной крышки, в котором учитываются потери энергии только за счет поглощения. Если ввести углы падения и преломления падающего луча ^ и ^ соответственно, то, согласно закона Бугера-Ламберта-Бера, получаем:

а = e - Kl c /cos ^ 2 = exp

- Kl c

^^ sin² ^^Л , I^-        )

здесь K — коэффициент экстинкции, а B — показатель преломления материала стеклянной крышки, l — толщина стеклянной крышки.

Стеклянная крышка накапливает энергию солнечного излучения W . Кроме того накопление энергии происходит также за счет теплообмена с окружающим воздухом с температурой Т посредством конвективного теплообмена, теплообмена с окружающей средой в длинноволновом диапазоне теплового излучения, с фотоэлектрической пластиной, находящейся при температуре Т_ф , через замкнутый воздушный зазор посредством комбинированного действия двух явлений — конвекции и излучения. Учитывая все сказанное выше, можно рассчитать коэффициенты теплопередачи на внешней поверхности в следующем виде:

(3) конв       в     ,

³ изл = ^(Т Конв + Т Изл ^)(Т_Кон_в + Т изл ) .

Здесь v_s — скорость ветра, заданная в м/с; а — постоянная Стефана-Больцмана; Т и ^_с — абсолютная температура и коэффициент излучательной способности рассматриваемого слоя. Если в , в , 0_вн — коэффициенты, задающие угол обзора поверхности стеклянной крышки относительно неба, земли и окружающей среды, то:

т 1 = в т_н 4 + в т 4 + в т 4 . изл      н н      с с      вн вн

Анализ результатов исследований показал, что температура внешнего фона практически не отражается на работе гибридной системы, комбинирующей фотоэлектрический преобразователь солнечной энергии водонагревательного устройства. Полученные результаты показывают, что при температуре воздуха 20 °С изменение Т от 0 до 20 °С приводит к изменению электрического и теплового прироста менее чем на 1,5%. Следовательно, для практического применения в зданиях Т можно принять таким же, как Т . Коэффициент теплопередачи внутренней поверхности можно задать следующим соотношением:

^ сп

= ( 3 )   + ( 3  )

изл сп       конв сп

а (Т с + Т^Т + Т п ) ₊ NvA

— +--1

l в

Здесь d и l соответственно теплопроводность и толщина рассматриваемых слоев. В работе [22–24] представлено соотношение, связывающее числа Нуссельта и Релея при наличии естественной конвекции между плоскими пластинами, расположенными параллельно. Тепло, которое поглощает пластина фотоэлектрического устройства, определяется следующим соотношением:

W n = Ф ( ^т , ) - Е п . (7)

здесь ZT ) — эффективная поглощающая способность пластины фотоэлектрического устройства, значение которой имеет вид:

( Zt „ ) =

ζ в ζ п τ п

1 - О - Тп )М

здесь ζ — коэффициент пропускания стекла, учитывающий только потери при отражении, а µ — коэффициент отражения стекла при условии диффузного падающего излучения. Возможна ситуация, когда часть излучения достигает пластины с поглощающим слоем. Такое возможно, если пластина фотоэлектрического устройства частично прозрачна х. В этом случае уравнения должны быть изменены, для учета процесса деления энергии излучения, поглощенной пластиной. Если возникает необходимость в дополнительном остеклении, то и в этом случае необходимо учесть, что энергия, поглощаемая пластиной, перераспределяется. В этом случае в модели появляется дополнительный блок, учитывающий этот фактор. Мощность постоянного тока Е , генерируемая гибридной системой, сильно зависит эффективности работы солнечного элемента η которая, в свою очередь, зависит от температуры окружающей среды. Если ψ — отношение площади элемента солнечной батареи к площади апертуры, то:

Еп = Φψсηэ

и

П э = П эт [1 - ^ эт ^(Тп ^- Т эт ^)]

здесь η КПД эталонной ячейки при эталонной рабочей температуре Т , а ω — температурный коэффициент.

Тепловой поток, перемещающийся от пластины фотоэлектронного преобразователя солнечной энергии к месту расположения металлического соединения трубы, проходит двумя различными путями: (а) через клеевой слой, затем вдоль поглощающей пластины и (б) вдоль пластины фотоэлектронного преобразователя солнечной энергии, затем через клеевой слой непосредственно к месту соединения труб. Вода в трубе отбирает тепло от соединительной системы посредством теплопроводности и конвекции. Принимая во внимание, что теплопроводность определяется проводимостью металлического соединения, получаем для теплопроводности следующее соотношение:

δ соед =

σd соед соед

l соед

здесь σ — теплопроводность металлического соединения, l — среднее значение толщины металлического крепления трубы, d — ширина металлического крепления трубы. Расчет конвективного теплообмена k можно провести, используя уравнение Диттуса-Белтера для полностью развитого турбулентного течения [25–27]:

Nv_д = 0,023 Q e °_д8 Pr^0,4 .

здесь N — число труб, v _д — скорость воды в трубах, О — тепловое сопротивление, Pr — число Прандтля. Для полностью развитого ламинарного течения:

к_Ко_Нв = 4,364

конв

d внутр

здесь d _внутр — внутренний диаметр трубы, 8_К0Н „ — коэффициент теплопроводности при конвекции. Средний коэффициент конвективной теплоотдачи при более точном расчете учитывает входные эффекты и режимы совместного действия вынужденной и естественной конвекций. Расчеты показывают, что:

--------- —--1--

3 В 3 nd L 3 L вт вт      конв    вн       соед здесь 3т — коэффициент теплопередачи воды в трубе, Вет— площадь внутреннего сечения трубы, L — длина трубы. Тепловой КПД гибридной системы — фотоэлектрический преобразователь солнечной энергии + водонагревательное устройство — определяется отношением тепловой мощности P , которую несет вода на выходе устройства, к соответствующему излучению Ф, приходящемуся на площадь сечения трубы В:

PТ

Ф а электрический КПД:

ЕР

Ф

Выводы

Разработана математическая динамическая тепловая модель гибридной системы – фотоэлектрический преобразователь и устройство нагрева воды, которая может быть применима для практического анализа подобной гибридной системы. Предлагаемая модель позволяет проводить оценку мгновенных характеристик гибридной системы, определять в любой момент времени производительность системы, состояние ее компонентов и, в конечном счете, при определенных условиях осуществлять всеобъемлющий тепловой расчет гибридной системы. Получены соотношения, позволяющие оценить тепловой и электрический КПД гибридной системы.