Моделирование гиперспектрометра на спектральных фильтрах с линейно-изменяющимися параметрами

В настоящее время одним из важных и приоритетных направлений развития средств и методов дистанционного зондирования земной поверхности является разработка и применение видеоспектрометров . До появления видеоспектрометров спектры отражения и излучения поверхности Земли мало использовались в качестве идентификационных признаков, хотя изучались десятки лет и были хорошо известны [1–4]. Это было связано с тем, что авиационные спектрометры имели низкое геометрическое разрешение, давали информацию только вдоль линии полёта и позволяли судить о спектральных свойствах лишь достаточно протяжённых объектов . В видеоспектрометрах реализуются принципы новой научной дисциплины – изображающей спектроскопии, когда помимо геометрических используются спектральные характеристики объектов. Появление видеоспектрометров связано с развитием новых технологий: с разработкой матричных приёмников, а также с появлением полихроматоров, обладающих высоким спектральным разрешением. В состав видеоспектрометров входят две системы. Во-первых, оптическая система, которая делит регистрируемую область пространства на набор смежных точек, и, во-вторых, изображающий спектрометр , который разлагает состав принятого электромагнитного излучения на набор ограниченных спектральных полос. В результате видеоспектральной съёмки формируется многомерное пространственно-спектральное изображение, в котором каждый элементарный участок изображения, «пиксел», характеризуется собственным спектром. Такое изображение носит название «куба» информации, два измерения которого соответствуют пространственному изображению местности на плоскости, а третье – характеризует спектральные свойства изображения. Спектральное разрешение современных видеоспектрометров достигает 1,8–2,0 нм и обеспечивает построение спектральных характеристик подстилающей поверхности, определяемой мгновенным полем зрения прибора (для авиационных видеоспектрометров – около 1 мрад [5, 6]).

По способу реализации пространственного разрешения известные гиперспектрометры могут быть разделены на следующие типы:

– pushbroom – сканирование по пространству происходит с помощью одноразмерного мгновенного поля зрения, которое перемещается только в одном направлении, обычно вдоль траектории носителя;

– framing – гиперспектрометры этого типа используют двухразмерное мгновенное поле зрения, которое сохраняется фиксированным (за счёт тангажного отслеживания) в течение процедуры сбора данных;

– windowing – новый класс гиперспектрометров, в которых двухразмерное мгновенное поле зрения движется непрерывным образом вдоль траектории носителя.

Для решения конкретных задач используются гиперспектрометры различных типов – дисперсионные, интерференционные и фильтровые. Большое количество задач может быть решено с помощью стандартных дисперсионных гиперспектрометров. В работах [7–10] представлено подробное описание компактного изображающего спектрометра (compact imaging spectrometer, COMIS), используемого в корейском микроспутнике STSAT3. Вес микроспутника составляет 150 кг при габаритах 85×82×100 см. Спутник помимо спектрометра также несёт многофункциональную систему инфракрасного наблюдения MIRIS (Multi-purpose InfraRed Imaging System), предназначенную для съёмки Галактики в ИК-диапазоне. В работах [5–33] приведены различные оптические схемы гиперспектрометров, используемые для зондирования Земли.

В качестве диспергирующего элемента в спектрометре может использоваться как призма, так и дифракционная решётка. Преимуществом дифракционной решётки по сравнению с призмой является компактность. Изображающие спектрометры, содержащие в качестве диспергирующего элемента дифракционную решётку, как правило, основаны на конфигурации Оффнера или конфигурации Дайсона. Ниже рассмотрены несколько примеров компактных спектрометров с дифракционными решётками, ориентированных на решение задач гиперспектрального анализа земной поверхности.

Однако, если задача выходит за рамки обычных исследований, требуется более высокое спектральное разрешение – используются интерференционные методы. При этом преимущества сканирующих Фурье-спектрометров зачастую оказываются избыточными и трудно реализуемыми, особенно в коротковолновой части спектра. Самым распространённым типом являются статические Фурье-спектрометры [33], построенные по схеме интерферометра Саньяка [33], на основе призмы-склейки (или поляризационного типа).

Оптические схемы спектрометров на фильтрах приведены в работе [33]. Преимущество спектрометров на фильтрах состоит в простоте и надёжности конструкции. Однако гиперспектрометры содержат в конструкции фильтры с изменяемыми по апертуре спектральными характеристиками [34–37].

Для того, чтобы сформировать гиперспектральный куб [2, 3], изображения, полученные с помощью гиперспектральной аппаратуры, необходимо подвергнуть процедурам обработки, фильтрации. Для этого необходимо знание аппаратных функций различного уровня, в частности, функции рассеяния точки. В случае гиперспектральной аппаратуры c дисперсионным элементом в виде решётки или призмы точка на изображении превращается в линию, каждая точка которой содержит информацию о спектральной характеристике. Обычно гиперспектрометр состоит из двух частей: телескопа и собственно гиперспектрального блока.

В случае гиперспектрометра на фильтрах каждая точка изображения проходит множество светофильтров. Для того, чтобы восстановить гиперспектральное изображение, требуется найти функцию рассеяния точки для каждого спектрального фильтра. Для этого необходимо разработать методы моделирования фильтрового гиперспектрометра. Методы моделирования телескопической части изложены в работе [38]. Предметом данной работы является моделирование гиперспектрального блока.

движении прибор фиксирует изменение интенсивности на приёмной фотоматрице. Это изменение связано с тем, что изображение точки проходит через спектральные фильтры с различными спектральными характери- стиками.

Пусть спектральный фильтр имеет функцию пропускания т ( £ , ю ), где параметр £ - параметр идентичности спектрального фильтра. Этот параметр зависит от координаты точки на фильтре £ ( x ). В качестве параметра £ будем использовать значение частоты света (длины волны), при котором пропускание спектрального фильтра имеет максимальное значение.

Количество энергии, падающее на регистратор в точке с координатой x , равно

Ф(^( x )) = J0”T(^( x ),ю) g (ю) d®.                (1)

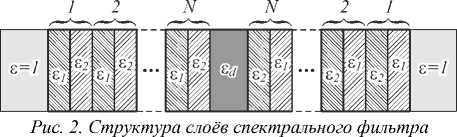
В качестве фильтра будем использовать слоистую структуру, состоящую из решётки Брэгга, представляющую систему слоёв с диэлектрической проницаемостью £ i , £ 2 . В середине этой структуры находится диэлектрический слой с показателем преломления £ 0 . Коэффициент пропускания зависит от толщины этого дефекта.

Фильтр с линейно-изменяющимися параметрами представляет собой вышеописанную слоистую структуру, у которой толщина дефекта изменяется от точки к точке. В результате получается, что частота, на которой наблюдается максимум пропускания, также зависит от точки на апертуре фильтра.

Следует отметить: так как в окрестности фотоматрицы формируется изображение точки, это означает, что на фильтр с линейно-изменяющимися параметрами падает сфокусированный сферический пучок. При прохождении светофильтра характерные размеры фокального пятна изменяются. Это приводит к ухудшению разрешающей способности фильтрового гиперспектрометра по сравнению с оптической схемой для панхромного наблюдения.

В качестве функции пропускания фильтра обычно используется Лоренцева или Гауссова форма.

Лоренцева форма для функции пропускания имеет вид [39]

т ( ^,% ) = a

f ²

(ХЧ) ² + f²

.

В простейшем случае параметры a, f не зависят от £, а параметр £ зависит от координаты по линейному закону

^ = ^ 0 + ^ x .                      (3)

Это справедливо для фильтра с линейно-изменяющимися параметрами. В общем случае зависимость коэффициента пропускания от координаты имеет вид

T ( x ,Х ) = a ( x )

f2 (x)         .

(Х-£( x ))2 + f2 (x)

Гауссова форма в простейшем случае имеет вид [39]

т(5,Х) = a exp

Г (е-м2J 2o2V 7

.

В простейшем случае (по аналогии с Лоренцевой кривой) параметр 5 зависит от координаты по линейному закону.

В общем случае функция спектрального пропускания имеет вид

т(5А) = a (5) exp

Г (5-X)2) V 2^2 (5) j

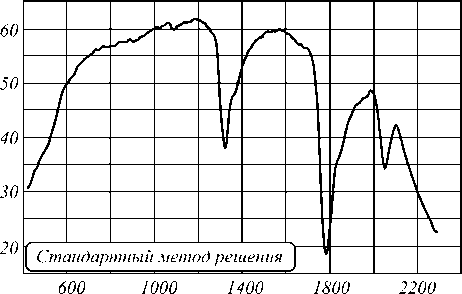
На рис. 1 приведены результаты восстановления спектральной характеристики. Восстановление проводилось с помощью решения интегрального уравнения (1).

Методы решения интегрального уравнения, используемые для решения, описаны в Приложении А и Приложении Б. Приведённые результаты были получены с помощью очень узкополосного фильтра с линейно изменяющимися параметрами. В этом случае погрешность восстановления спектральной характеристики не превышает 1 %. Исходная функция, изображённая на рис. 1 а , в , представляет собой сигнал, полученный с помощью фильтрового гиперспектрометра. График, показанный на рис. 1 б, г , представляет собой спектральную характеристику, восстановленную с помощью решения интегрального уравнения. Небольшое различие в этих графиках обусловлено узкой спектральной характеристикой используемого фильтра. При увеличении ширины пропускания фильтра графики начинают отличаться друг от друга.

(						V	w
							V
								"Г
	[ Исходная функция ]

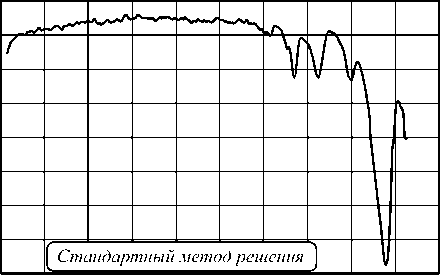
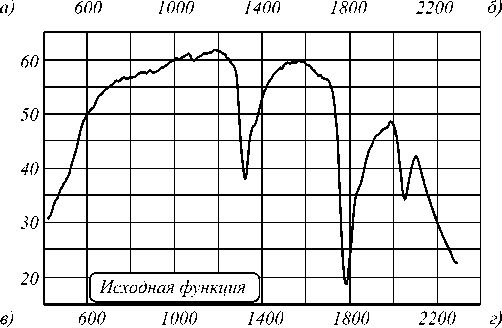
Рис. 1. Результаты восстановления спектральной характеристики

600      1000     1400     1800     2200

2. Решение задачи о прохождении электромагнитных волн через слоистые структуры на основе разложения по каноническим бездифракционным ТМ- и ТЕ-поляризованным пучкам

Во многих оптических приложениях необходимо решать задачу прохождения бездифракционной волны через металлический или диэлектрический слой. Бездифракционные (самовоспроизводящиеся) волновые пучки обладают общим интересным свойством: при распространении в свободном пространстве у них изменяется только фаза, но не изменяется распределение комплексной амплитуды. Некоторые безди-фракционные пучки обладают ещё одним замечательным свойством: они представляются в виде

функции с разделяющимися переменными. Будем называть бездифракционные пучки с разделяющимися переменными каноническими бездифракционными пучками. В общем виде бездифракционные пучки имеют следующий вид

W = w ( x 1 , x ² ) exp Г ik Y x 3 ] ,                           (7)

W

TM

^Y e i

V г e 2 j

exp Г ik Y x 3 ] ,

W =

TE

^- e- 2

Y e 1

exp Г ik Y x ³ ^ ,

Y - постоянная распространения бездифракционного пучка, £ - диэлектрическая проницаемость.

где e =

Г dF3J 5x1

ЦV ОX J

' A. ( ^a 1 ^a 2 )' ^ B 0 [^^a 1 ^a 2

= 4П J (Y(e0 ’a) Qa-a21

X E ₀ V y 1 , y ² J exp ( — ik a y ) d² y .

e ₂

f г; xv л gL g"■x

- v g F

V g 11 d x ¹ J

где функции F 3 удовлетворяют уравнению Гельмгольца

A F 3 + k ² Г e-y ² J F 3 = 0 ,

e - диэлектрическая проницаемость среды, g_ik - компоненты метрического тензора в криволинейной системе координат x ¹ , x ² , x ³ – криволинейные координаты.

Пучки W TM называются пучками поперечно-магнитного типа. Они не имеют продольной составляющей магнитного поля. Пучки W TE называются пучками поперечно-электрического типа. Они не имеют продольной составляющей электрического поля.

Рассмотрим разложение результирующего поля в виде суперпозиции бездифракционных ТМ- и ТЕ-поляризованных пучков. Формальная теория представления решения системы уравнений Максвелла в виде суперпозиции бездифракционных пучков изложена в Приложении В. В однородной среде выраже-

ние для пучков имеет вид:

w TM

' Y ( ^e 0 ^,a ) e a 1 a ₂1

j

V

^e o e a ₁ a ₂2

exp Г ik Г y ( e ₀ ,a ) x ³

Г

—j

J

где

w

TE

-p ea! a- 2

J

V Y ( ^e 0 ,^a ) e aa - 1 J

exp Г ik Г y ( e ₀ ,a ) x ³

^e 0

a -

a - .

Рассмотрим только компоненты электрического

поля

^E V ^x 1 , ^{x 2} , ^x 3 ^J = J ( Y ( ^e 0 ^,a ) Q _ai a - 1 , ^— Q a,a - 2 ) ^X

f A ( ^a 1 ^a 2 ) ^J X

^B0 [ ^a 1 ^a 2 ]

^J J

При x ³=0

exp Г ik V a x + 7^ ,a ) x ³ J J d² a .

) — 1

X

Далее после прохождения слоистой среды компо-

ненты электрического поля имеют вид

' A ( ^a 1 ^a 2 ) J =^Г T_T m    0 ^J [ A 0 ( ^a 1 ^a 2 )'

B Г a 1 a 2 J   V 0 T_Te J[ B 0 Г a 1 a 2 J ,

' A ( ^a 1 ^a 2 )' B Г a 1 a 2 J

= ^ ^{J T} ( Y^(e 0 ’^{a) Q} “ - a ₂1

— 1

^{— Q} a,a ₂2 ) ^X

X E ₀ Г y 1 , y ² J exp ( — ik a y ) d² y .

Объединяя формулы, получаем выражение для

компонент электрического поля после прохождения слоистой структуры

^{E Г x} 1 , ^{x 2} , ^{x 3 J} = ^J ( Y ( ^e 0 ^,a ) Q _a , a ₂1 , ^— Q _a , a ₂2 ) ^X

ГA (a1a2 )'

B Г a 1 a 2 J

V ^{V        J} J

exp Г ik Г a x + Y ( e ₀ ,a ) x ³ J J d² a .

Приведённая формула в дальнейшем будет ис-

пользована для моделирования пятна рассеяния точки при прохождении спектрального фильтра.

• 3.    Расчёт коэффициента отражения и пропускания на квазипериодической системе диэлектрической системы слоёв

• 3.1.    Решение в однородной среде

В данном разделе рассмотрено распространение волны в структуре, представляющей систему слоёв с диэлектрическими проницаемости e 1 , e ₂ и толщинами d 1 , d 2 соответственно. В середине структуры находится дефект, представляющий собой слой с диэлектрической проницаемостью e ₀ и толщиной d ₀. Первый и последний слои имеют диэлектрическую проницаемость e 1 . Непосредственно к дефекту прилегает слой с диэлектрической проницаемостью e 2 .

Для случая плоских волн базовые методы изложены в работах [39–41]. В данной работе приведены методы, инвариантные к выбору бездифракционных пучков.

В случае ТМ-поляризации решение системы уравнений Максвелла представляется в виде

^E 0 ^Г x ¹, x ^{2 J} = J ( y ( ^e 0 ^,a ) Q _a 1 a ₂1 , ^— Q a , a ₂2 ) ^X

' A ( ^a 1 ^a 2 )' B 0 V ^a 1 ^a 2 J

exp ( ik a x ) d² a ,

W =

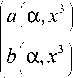
e a 1

e a 2

J

( Y ( ^e 0 ^,a ) ^Q a , a ₂1

—

^Q aa ₂2 )

'A. (a1a2 )'

^B 0 V ^a 1 ^a 2 ^J

= T" ^{J E} 0 ^Г y *’ y² 4 n ^V

exp ( — ik a y ) d a 1 a ₂.

Получаем коэффициенты разложения по

ТЕ- и

ТМ-волнам

В дальнейшем для базисных векторов в декартовой системе координат будем обозначать e ^1 = e _{a 1}, e _a , _{a 2}2 = e _{a 2}. Индекс a= ( a 1 ,a ₂). Для цилиндрической системы координат a = ( a, m ), где m - число, входящее в exp ( im ф ), которое определяет угловую зависимость базисных функций от угловой переменной.

Подставляя это представление в уравнения Максвелла, получаем, что уравнение для функций

a ( a, x 3 ), b ( a, x 3 ) в однородной среде с диэлектриче-

ской проницаемостью ε имеет вид i_ d [a {x3 J] = _ Г0 e-1y2 (E,a)Va {x3У k dxb[x3 J,    Vг       0 jbГx3 J,

где y ( e ₀ ,a ) = ^ e ₀ -a 2 -a 2 .

Решение в однородной среде с диэлектрической проницаемостью ε имеет вид

Г a I x31

= G ( e,a ) U Г e, a, x 0 , x₁ , x ³

( + J c¹

c ^{_ _}

V 1 J

,

Г ^J a «I v b Г x3 Jy

где F 2 =

= G ( e ₂ ,a ) U Г e ₂ ,a, x 1 , x ₂ , x ³ J F 2 ,

l f ’ I f ^_

V^J J

.

Условие непрерывности требует непрерывности при x ³= x 1

G ( E i ,a ) U ( E i ,a, x о , x i , x i ) F = = G ( e ₂ ,a ) U ( e ₂ ,a, x 1 , x 2 , x 1 ) F 2 .

Здесь x ³ – текущая координата вдоль периодиче-

V V J J

G ( E i ,a ) = ( g i ( E_pa ) g 2 ( E i ,a ) ) ,

,       Г y(e,«) J     ,       Г-y(e,«) J g 1 (E,a) = l           I, g2 (E,a) = l             I,

V E J            V E J

U Г E,a, x 0 , x₁ , x ³ J =

ской структуры, x i – координата начала или конца ди-

электрического слоя.

Условие сшивки между вторым и третьим слоем

имеет вид

G ( e ₂ ,a ) U ( e ₂ ,a, x 1 , x 2 , x 2 ) F 2 = = G ( E 1 ,a ) U ( e, a, x 2 , x 3 , x 2 ) F ₃.

exp V ik y ( e, a ) V x ³ - x 0

J

По аналогии условие сшивки между нечётным и чётным слоем имеет вид

V

exp Г - ik y ( e,« ) Г x ³

.

^x 1 ] ] ]

В случае ТЕ-поляризации решение системы урав-

^{G (e} i , ^{a) U (e} i , ^a, ^x 2 n - 2 , ^x 2 n - 1 , ^x 2 n - 1 ) ^F 2 n - 1 = ^{G (e} 2 ,^{a) U (e} 2 ,^a, ^x 2 n - 1 , ^x 2 n , ^x 2 n - 1 ) ^F 2 n .

нений Максвелла представляется в виде

Условие сшивки между чётным и нечётным слоем

W =

_ a I a, x

Г

Уравнение для функций a m (α, x ³), b m (α, x ³)

родной среде имеет вид

i d Г aГ x 3 JJ = _ Г   о k dx3 b[x3 J " VY2 (E,a)

Г ^J a ( x )

_V ^{b Г x 3 J} _y

в одно-

имеет вид

G ^(e 2 , ^a) U ^(e 2 , ^a, x 2 n - 1 , x 2 n , x 2 n ) F 2 n =

= ^G ( ^E 1 , ^a ) ^U ( ^E 1 , ^a, ^x 2 n , ^x 2 n + 1 , ^x 2 n ) ^F 2 n + 1 ,

где x n – координата границ слоёв. Первая граница, непосредственно прилегающая к внешней среде, имеет координату x ₀.

Эти выражения можно представить в виде

A 1 F 2 n - 1 = B 1 F 2 n ,                                     (37)

Решение в однородной среде с диэлектрической проницаемостью ε имеет вид, аналогичный виду для

ТМ-поляризации. Однако матрица G (ε₁,α) имеет вид

G ( E i ,a ) = ( g i ( E i ,a ) g 2 ( E i ,a ) ) ,

Г y(e,«) J            Г-Y(E,a) J gi(E,a) = l 1 7 I, g2(E,a) = l     1 7 I.       (28)

VEJ VEJ

C1F2 n = D1F2 n+1.(38)

Связь между коэффициентами в двух нечётных слоях имеет вид

F2 n+1 = Q1F2 n-1,(39)

Q1 = U1R1, R1 = В- A1, U1 = Df1 C1.(40)

Связь между нечётным и чётным слоем имеет вид

F2 n+2 = R1F2 n+1.(41)

3.2. Сшивка решений на промежуточных слоях

до дефекта

Рассмотрим теперь распространение света в слоистой среде, состоящей из двух периодически повторяющихся слоёв с диэлектрическими проницаемостями ε 1 , ε 2 .

Решение в среде с показателем преломления ε 1

имеет вид

г ^J a x v b V x3 Jy

= G ( E_pa ) U Г E ₁ ,a, x 0 , x ₁ , x ³ J F₁ ,

где G ( E i ,a ) = ( g 1 ( E 1 ,a ) g 2 ( E 1 ,a ) ) , F =

l^r ] . f _

V^J 1 J

Используя полученные соотношения, получаем связь между коэффициентами в первом слое и слоем с нечётным и чётным индексом

F2 N+1 = Q1NF1,

F2 N+2 = R1Q1NF1.(43)

Матрицу Q 1 можно представить в виде

Q1 = P-1Q1 dP,(44)

где Q _{1 d} – диагональная матрица

F2N+1 = Q1NF1, F2N+2 = R1 (P-1QNP) F1.(45)

Решение во втором слое имеет вид

Диагональная матрица Q ₁ ^N _d имеет вид:

N ^ 1   ⁰

¹ d ” о %₂ .

V 2 J

Собственные числа λ1, λ2 являются решением уравнения

det ( Q 1 -X I ) = 0 .

где G ( е ₂ ,а ) = ( g 1 ( е ₂ ,а ) g ₂ ( е ₂ ,а ) ) , В 1 =

Решение во втором слое имеет вид

( + )

5 ^-

V 1 J

.

Ниже будет показано, что собственные числа можно найти, если известна дисперсионная зависимость.

3.3. Расчёт прохождения через периодическую слоистую структуру с использованием дисперсионной зависимости

В случае периодической структуры уравнение непрерывности при x ³= x ₁ имеет вид

G (^ а ) U ( г_ра, x о , X i , x ) F i = = G ( e ₂ ,а ) U ( £ 2 ,а, x 1 , x ₂ , x 1 ) F 2 .

С другой стороны, для разрешённой длины волны

связь между второй и нулевой границей имеет вид

G ( e ₂ ,а ) U ( £ 2 ,а, x 1 , x ₂ , x ₂ ) F 2 =

= exp ( ik d d ) G ( £ 1 ,а ) U ( £ 1 ,а, x ₀ , x 1 , x ₀ ) F ,

k_d – определяет моду, которая распространяется внутри периодической структуры, -п / d <  k_d < п / d , где d = d ₁+ d ₂ – период периодической структуры.

Эти уравнения можно переписать в виде

A 1 F = B 1 F 2 , C 1 F 2 = exp ( ik d d ) D 1 F 1 ,             (50)

F 2 = B ^- A 1 F 1 , C 1 F 2 = exp ( ik d d ) D 1 F 1 .            (51)

Исключаем F 2 , получаем систему однородных уравнений

( D 1 ^{- 1} C 1 B 1 ^{- 1} A 1 - exp ( ik d d ) I ) F 1 = 0.                 (52)

Для существования ненулевого решения необходимо, чтобы выполнялось условие det (Q1 - exp (ikdd) I) = 0,                        (53)

где

Q 1 = D - C 1 B - A .

Это условие представляет собой уравнение для определения дисперсионной зависимости X = X ( k_d ), где k_d е [ -л/ d , п/ d ] . Учитывая этот факт, матрица

Q ₁ ^N _d имеет вид

_qn = [ exp ( ik d d )        ⁰      )

^{1 d}   V 0       exp ( - ik d d ) J

Действительные значения k d соответствуют зоне пропускания, мнимые значения – запрещённой зоне.

3.4. Сшивка решений после дефекта

Рассмотрим теперь распространение света в слоистой среде, состоящей из двух периодически повторяющихся слоёв с диэлектрическими проницаемо-стями £ 2 , £ 1 . Слой, непосредственно прилегающий к дефекту, имеет координату y ₀.

Решение в среде с диэлектрической проницаемо-

стью £ 2 имеет вид

= G ( £ 2 ,а ) U ( £ 2 ,а, у 0 , У 1 , у ³ ] В ,

( a (у )

V

где В ₂ =

= G ( е ₂ ,а ) U ( £ ] ,а, У 1 , у 2 , у ³ ] В 2 ,

^J J

( +^

⁵ 2

5 ^- ,

.

Условие непрерывности требует непрерывности при y ³= y 1

G ( £ 2 ,а ) U ( E 2 ,а, у 0 , у 1 , у 1 ) В 1 = = G ( е ₂ , а ) U ( е ₂ , а, у 1 , у 2 , у 1 ) В 2 .

Условие сшивки между вторым и третьим слоем имеет вид

G ( е ₂ ,а ) U ( е ₂ ,а, у 1 , у 2 , у 2 ) В 2 = = G ( е ₂ ,а ) U ( е ₂ ,а, у ₂ , у ₃ , у ₂ ) В ₃.

По аналогии условие сшивки между нечётным и чётным слоем имеет вид

G ( ^£ 2 , ^а) U ^(e 2 , ^а, ^у 2 n - 2 , ^у 2 n - 1 ^у 2 n _ ₃ ) ^В 2 n _ ₃ = G ( ^£ 1 , ^а) U ( ^£ 1 , ^а, ^у 2 n - 1 , ^у 2 n , ^у 2 n - 1 ) ^В 2 n .

Условие сшивки между чётным и нечётным слоем имеет вид

G ( ^£ 1 , ^а) U ( ^£ 1 , ^а, ^у 2 n - 1 , ^у 2 n , ^у 2 n ) ^В 2 n

= G ( ^£ 2 , ^а ) ^{U (£} 2 , ^а, ^у 2 n , ^у 2 n + 1 , ^у 2 n ) ^В 2 n + 1 ^.

Эти выражения можно представить в виде

A 2 В 2 n - 1 = В 2 В 2 n ,                                     (63)

Г V = П V

2 2 n ⁼ 2 2 n + 1 .

Связь между коэффициентами в двух нечётных слоях имеет вид

В 2 n + 1 = Q 2 В 2 n - 1 ,                                         (65)

Q, = UR , U, = D, ¹ C, , R = В ,¹ A .

2     22    2     2   2    2     2 2

Связь между нечётным и чётным слоем имеет вид

^В 2 n + 2    R 2 ^В 2 n + 1 .

Используя полученные соотношения, получаем связь между коэффициентами в первом слое и слоем с нечётным и чётным индексом

В 2 N + 1 = Q 2 В 1 , В 2 N + 2 = R 2 Q 2 В 1 .                   (67)

3.5. Сшивка решения в области дефекта

Решение на последнем слое перед дефектом

= G ( £ 2 ,а ) U [ £ 2 ,а, x 2 n - 1

x ³

, ^x 2 N , ^x J¹ 2 N .

Решение внутри дефекта имеет вид

^G ( ^£ 0 ,^а ) ^U V ^£ 0 , ^а, ^x 2 N , ^у 0 , ^x J ^D .

Решение на первом слое после дефекта

= G ( e ₂ ,a ) U I £ 2 ,a, y 0 , y 1 , x ³ 0 S 1 .

Сшивка решений при x _{2 N} имеет вид

G ( £ 2 ,

a) U (£2 ’ a, x2N-1

’ ^x 2 N

’ ^x 2 N

) F2 N =

= G(£0,a)U(£0,a, x2N, y0,x2N)D.

Сшивка при y 0 имеет вид

G (£o, a) U (£o , a, x2n , y0, y0 ) D = G (£2 ,a) U (£2 ,a, y 0, y1, y 0) S1.

Полученные уравнения можно записать в виде

AF 2 n = D ,                                 (73)

C 0 D = D 0 S 1 ,                                  (74)

s 1 = Q 0 F 2 n , Q 0 = и 0 R 0 , и 0 = d 0 ^{- 1} c 0 , R 0 = в 0 ^{- 1} A .

3.6. Сшивка на первом и последнем слое для ТМ-поляризации

Выражение для поля со стороны падающего пучка

w

TM

' ^e a l 0

0 OfY(£,a)

I

e 7

a 2 J

£

exp I ik Y I x ³ - x ₀ 00 -

T

TM

I _ ea1

I

⁰ 7

e a 2 J

Y(£,a)£(£,a)

¹ e a l

I ⁰

e a 2

M TM ^S 2 N ’ J

M TM   ^{G (£} 2 ’^a ) ^{U (£} 2 ’^a’ y 2 N - l ’ y 2 N ’ y 2 N ) ^.

Решая полученную систему из трёх последних уравнений, находим выражение для коэффициентов отражения и пропускания для ТМ-поляризации

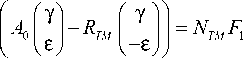
I y(£’«) 0

T v ’ = M

TM I             I TM 2 N .

I £(£,a) J

Связь коэффициентов на первом и последнем слое до дефекта имеет вид

F 2 N = R l Q l ^{N - l} F l .                                   (86)

Связь коэффициентов на первом и последнем слое после дефекта имеет аналогичный вид

S 2 N = R 2 Q 2 ^{N - l} S l .                                   (87)

Связь между S ₁ и F _{2 N} имеет вид

-R

TM

e a , I 0

0 JIY(£,a) ea2 1 -£

x ³ - x ₀

.

^S l = ^Q 0 F 2 N .

Решение в первом слое имеет вид

В результате получаем замкнутую систему уравнений для определения коэффициентов отражения и пропускания диэлектрической структуры. В Приложении Г приведён пример расчёта всех матриц для

w = " TM

f0 a I x J e a l

b | x J e a 2 ₇

e ₁

e 2 J

a ( x ³

. 0

случая нормального падения волны на структуру, имеющую на центральной длине волны пропускание, равное единице.

I I J J

где выражение для a ( x ³) , b ( x ³)

I < 1

a I x ³

. 0

= G ( e, a ) U | £,a, x ₀ , x 1 , x ³ 0 F 1 .

I I J J

Условие непрерывности при x ³ = x ₀ имеет вид

' eal s 0

= I e a '

Y

e

'a 2 J

£

Y

R ‘ rtm I

I -£

3.7. Сшивка решения на первом и последнем слое для ТЕ-поляризации

Выражение для поля со стороны падающего пучка

I

W TE = ^B 0

+ R_Tr

TE

—j

" e a 2 0

0 I al J

x 0 ⁰⁰

x

+

I

^- e a 2

⁰ 1 a l J

I exp I - ik Y I x

-

I

TV TM

e a 2 J

N F,

TM 1 ,

Решение в первом слое имеет вид

= G (e1, a) U (£pa, x0, x1, x0).

Поле на выходе имеет вид

W = T " TM   t™

I_ ea1

I ⁰

Y Y

e о a 2 J

£

(•7a / 3 exp I ik Y I y

Поле в последнем слое

w

TM

( <31

a I y J e a l

b | у J e a 2

J

^{e a 1}

_i 0

e о a 2 7

где

^{G (£} ' ,^{a) U} I ^£ ' ,^a, y 2 N - ' , y 2 N , y J ^S 2 N .

w =

TE =

I0

^- a I ^x 0 ^e a 2

I bIx3 0eal J

^I I - e _{a 2}

I _I 0

e 1

a l J

где выражение для a ( x ³) , b ( x ³)

a f y 3

I

. 0

J

Условие непрерывности тангенциальных компо-

нент при y _{2 N}

I0 a ( x )

. b I ^{x 3} 0,

G ( £,a ) U I £,a, x ₀ , x , , x ³ 0 F .

Условие непрерывности при x ³ = x ₀

I

^I I - e _{a 2}

I

^I I - e _{a 2}

e a l J

e a l 7 1

B 0

N F

TE 1 ,

Nte = G(£',a)U(£',a,x0,x,,x0).

Поле на выходе имеет вид

TE

= т

TE

- e a 2

e a l

- y 2 N JJ .

Поле в последнем слое

рез спектральный фильтр (рис. 2) со следующими параметрами: 8 _l = 2,25 , 8 2 = 6,25 , 8 d = l, d _l =% ₀/6, d ₂ = 0,l % ₀, d ₂ = 0,5 X 0 , X ₀ = I mkm .

где

w =

TE

(                1

a ( У J e a l

^Ь l У ³ J e “ 2 ,

( a lУ

. J

. b l y ³1

(eal l 0

e a 2

G ( ⁸ l ,^a) U 1 ⁸ l ,^a, ^y 2 N - 1 , ^y 2 N , ^y J ^S 2 N .

Условие непрерывности при y _{2 N}

(

T

TE

e a 2

⁰ ( ¹ J = e a l e a l J lYJ l 0

e a 2

J

^MTE^S 2 N ,

J

^MTE   ^{G (8}p^a ) ^{U (8} l ,^a, y 2 N - l , y 2 N , y 2 N ) ^.

Решая полученную систему из трёх последних уравнений, находим выражение для коэффициентов отражения и пропускания для ТЕ-поляризации

( l JB0I I + R-l YJ '

- ( l J | = TV F

¹ TE I       II T'TE l ,

' YJJ

(l J-M

T TE I I = ^Mte^S 2 N .

l YJ

Связь коэффициентов на первом и последнем слое до дефекта имеет вид

F 2 N = R l Q N ^{- l} F l ,

S 2 N = R 2 Q 2 N ^{- l} S l .                                 (l0l)

Связь между S ₁ и F _{2 N} имеет вид

S l = Q 0 F 2 N .                                    (l02)

В результате получаем замкнутую систему уравнений для определения коэффициентов отражения и пропускания диэлектрической структуры.

4. Прохождение сферической волны через спектральный фильтр

Рассмотрим прохождение немонохроматической сферической волны через спектральный фильтр. Рассмотрим случай, когда спектральный фильтр расположен в области изображения объекта, который в нашем случае представляет точку, излучающую немонохроматический пучок. В этом случае фильтр расположен в окрестности фокуса сферического пучка. Для расчётов будем использовать локальное приближение, которое заключается в том, что характеристики спектрального фильтра слабо изменяются в окрестности пятна рассеяния. Это позволяет нам свести решение задачи о прохождении сферической волны через фильтр с линейно-изменяющимися параметрами к задаче о дифракции сферической волны на ква-зипериодической системе слоёв, которая была рассмотрена выше.

В качестве примера рассмотрим прохождение Гауссова пучка со сферическим волновым фронтом че-

На рис. 3 показаны графики пропускания такой структуры в зависимости от длины волны падающего нормально излучения при различном количестве слоёв N в периодической структуре.

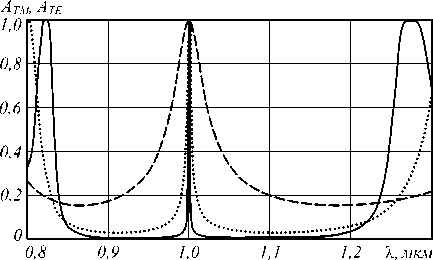
Рис. 3. Зависимость коэффициента пропускания спектрального фильтра от длины волны при N=3 (пунктирная линия), N=5 (точечная линия), N=7 (сплошная линия)

Очевидно, что с увеличением числа слоёв запрещённая зона вокруг базовой длины волны X ₀ = l мкм становится более выраженной, хотя размер её уменьшается. Также зависимость коэффициента пропускания в области базовой длины волны с увеличением N приближается к виду 5 ( X - X ₀): отношение ширины центрального пика по полуспаду от максимума к базовой длине волны равна 0,058 при N =3; 0,0068 при N =5; 0,0009 при N =7.

Если излучение будет падать на спектральный фильтр под углом к оптической оси, то пик пропускания будет смещаться. Причём смещение для TE- и ТМ-поляризации будет различным. На рис. 4 показаны графики пропускания рассматриваемой структуры ( N =7) в зависимости от длины волны для излучения, падающего под углом 23,6 ° . Хорошо видно, что происходит значительное смещение центрального пика, а также различие картины для TE- и ТМ-поляризации.

Данный факт свидетельствует о том, что при использовании спектрального фильтра в короткофокусной оптической системе (лучи идут под большими углами к оптической оси), будет происходить искажение пятна рассеяния и, соответственно, изображения.

На рис. 5, 6 показаны результаты дифракции Гауссова пучка с различной числовой апертурой в свободном пространстве и с использованием спектрального фильтра. Обозначим через т отношение максимального значения в фокусе для свободного пространства к максимальному значению с использованием фильтра.

Также будем учитывать соответствующие отношения размеров фокального пятна п .

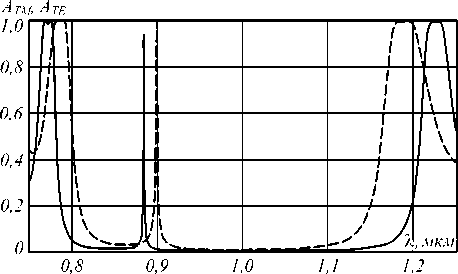
Рис. 4. Зависимость коэффициента пропускания спектрального фильтра от длины волны при N = 7 для излучения, падающего под углом 23,6° при TE-(пунктирная линия) и ТМ- (сплошная линия) поляризации

спектральным фильтром с линейно-изменяющимися параметрами. В дальнейшем теория, приведённая в данной работе, будет использована для расчётов характеристик гиперспектрометров, используемых для дистанционного зондирования Земли.

Работа выполнена при поддержке Министерства образования и науки РФ и грантов РФФИ №14-07-97008 и 13-07-12181.

Приложение А. Решение интегрального уравнения с использованием регуляризации Тихонова

Пусть интегральное уравнение имеет вид

F ( z ) = [ T ( z ,to ) g ( to ) d to .

a

Функционал невязки имеет вид e= (d ([bT(z,to)g(to)dto-F(z))2dz +

(А1)

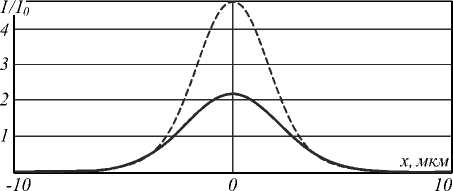
Рис. 5. Распределение в плоскости фокуса для NA=0,8 в свободном пространстве (пунктирная линия) и при использовании спектрального фильтра (сплошная линия)

+4 q о ( to ) g ² ( to ) + q 1 ( to ) V

^d g ^(to) Y" d to I

7 J

(А2)

d to ,

где ц , q ₀ ( to ) , q 1 ( to ) - положительно определённые весовые функции, которые приводят к регуляризации решения.

Запишем этот функционал в конечных разностях. Функционал в этом случае превращается в функцию

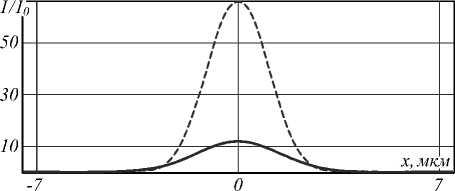
Рис. 6. Распределение в плоскости фокуса для NA=0,18 в свободном пространстве (пунктирная линия) и при использовании спектрального фильтра (сплошная линия)

M-1 V N-1

e=ElE T (zp ,toi Jg (to i )Ato-F (zpJIx p=0 V i=0

( N—I x l E T (zp,tokJ g (to k )Ato-F (zpJIAz+

V k=0

N - 1

+цЕ q 0 (toi) g2 (toi )Ato+ i=0

+ц Е »(» , ) ( 5 ^^ . +^ J a_m .

1 "0       V Ato J

(А3)

На рис. 5 числовая апертура равна NA=0,8 ( т = 2,18; п =0,78), а на рис. 6 рассмотрена более острая фокусировкаNA = 0,18 ( т = 5,5; п =0,74).

Как видно из приведённых результатов, с увеличением числовой апертуры (остроты фокусировки) при использовании спектрального фильтра происходят всё большие потери энергии, связанные с блокировкой лучей, идущих под большими углами к оптической оси. Также наблюдается уширение размера фокального пятка по сравнению с фокусировкой в свободном пространстве.

Заметим, что потери энергии в данном случае являются более значительными, чем уширение фокаль-

zp ,toi - отсчёты по соответствующим переменным, Ato, Az - шаги дискретизации по соответствующим переменным. Полученное выражение можно переписать в виде е =

M - 1 ( N - 1                   V N - 1                   J

= E l E T i^p g‘ Ato- F^p E T kp g^k Ato- F p \ A z + (А4)

p = 0 V i = 0                      J V k = 0                       J

N - 1

(

+^ E q 0 V g i

i = 0

V

ного пятна.

Заключение

В работе получены результаты, позволяющие оценить возможность использования гиперспектрометра со

j 2 i

I _J + q ₁

^V g i ^{+ 1}

-

gi

_V Ato

J ² J

I I Ato .

^I I I

J J

Полученная функция зависит от отсчётов неизвестной функции. Для минимизации приравняем производные к нулю и получим систему линейных уравнений de

0.                                          (А5)

d g

Итого получаем систему линейных уравнений

N — 1 m — 1

£ l £ T sp T kp Дю I g^k —

^ k = 0 ^ p = 0              )

' M — 1

£ Ts-F p ДДю+

( p = 0

+ц ( q 'У + ( Дю ) 2 ( q s ^{— 1} g s — q s ^{— 1} g s ^{— 1}

(А6)

—I

■ qv ⁺ 1 + q s g s ) ) Д® = 0,

N — 1 A m - 1              A

£ £ TspTkpДю| gkДz — k=0 ^ p=0            )

k —k     — 2 k — — 1 _ k o s Jc k o s

• ^—Ц ( q 0 g ⁺ h ( q 1 g 5 k ⁺ q_xg 5 _k ^—

M — 1

• — q k ^—1 g^{k —} 1 5 k — qg ⁺¹5 k ) = £ T sp F p .

p = 0

Решая полученную систему уравнений,

(А7)

получаем

отсчёты функции, которая является решением интегрального уравнения.

Приложение Б. Решение интегрального уравнения с помощью аппроксимации линейными сплайнами

Разбиваем весь участок интегрирования на N участков. В этом случае точек интегрирования будет N + 1. На каждом из участков искомая функция представляется в виде линейного сплайна

f ( x ) = У . + y i ^{+ 1} y i ( x — X i ) .                         (Б1)

x i + 1 ^- x i

В результате интегральное уравнение превращается в функциональное уравнение вида.

N _x

F ( ^z ) = £J" ' T ( z , x ) f ( x ) dx .                 (Б2)

i = 1 x^x-

Подставим теперь к (x ) = У- + y+1 _ y" (x — xi).

x_{i + 1} - x_i

Если сетка равномерная, обозначим Д г = x i + 1 — x i :

fi ( x ) = У" + y i ⁺ 1 y i ( x — x ) . (Б3) A x

В результате для определения y i получается система линейных уравнений. Систему уравнений можно переписать в следующей форме

j = bj,(Б4)

где матричные элементы Aⁱ_j имеют вид

A^ = (Ax)—1/(Д T(zj, У + x1} (^ — У)dУ ,

Aj = (Ax ПЛ T (zj, y + x )(Ax — y)+_

(Б6)

⁺ T ( Z j , y ⁺ x i — 1 ) y ) d y ,

AN+1 =(AxH^ T(zj-,у + xn }у dу .(Б7)

Столбец правых частей имеет вид bj= F^zj-}.(Б8)

Решаем полученную систему линейных уравнений, получаем отсчёты функции, которая является

решением интегрального уравнения.

Приложение В. Формальное решение системы уравнений Максвелла в различных представлениях

При решении системы уравнений Максвелла воз-

никают трудности, связанные со сложным представлением решений. Часто полученные решения трудно

анализировать из-за отсутствия компактного представления. Известно, что удобная математическая запись полученных решений позволяет проанализировать свойства полученных решений. Наиболее ярким примером является использование тензорной записи для уравнений общей теории относительности, механики сплошной среды или операторная запись уравнений в квантовой механике и квантовой теории поля. Знаменитые диаграммы Фейнмана позволили решать сложные задачи в квантовой электродинамике. Компактная запись выражений уменьшает количество ошибок, возникающих при выводе математических формул. Систему уравнений Максвелла в произвольной системе координат можно записать в виде эволю-

ционного уравнения:

i d W Ax 1, x2, x3}} k       dx3

= uW A x 1 , x ², x ³}},

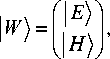
(В1)

где E – тангенциальные компоненты электрического поля, H – тангенциальные компоненты магнит-

ного поля.

Выберем в пространстве решений счётный (дискретный) базис; ( x ¹, x ²) – криволинейные координаты в плоскости, перпендикулярной оптической оси, x ³ – координата вдоль оптической оси. Обозначим базисные функции e „ _ms ( x 1 , x ²)}. Индексы n , m , s нумеруют базисные функции. Третий индекс обычно зависит от типа поляризации и направления распространения волны. Представим решение уравнения Максвелла в виде разложения по базису

| W A x ¹, x ², x ³)) = q^nms A x ³ )| e n _m s ( x 1 , x ²)).

(В2)

Набор функций q^nms ( x ³) будем называть решением в Q-представлении. Каждому абстрактному оператору в данном базисе можно сопоставить многомерную матрицу U_n^p_m^q_s^k

u \ e nms ( x 1 , x 2 )) = U m A x ³) | e -qk ( x ¹, x ²)) .             (В3)

Система уравнений Максвелла в Q-представлении записывается в виде

i d q m* ⁿ k d x³

_ TT^mns A ³ } pqk A ³ } ^U pqk ( x ) q ( x ) .

(В4)

В случае, когда набор базисных функций не является счётным, суммирование в формулах заменяется на интегрирование. В общем виде решение системы уравнений Максвелла можно представить в интегральном виде

W = Xj -T q ' ¹ ( x ³ JI e —— 2 S) d ® 1 d ® ² •              (В5)

s

Система уравнений Максвелла сводится к интегро-дифференциальному уравнению

—— 2 .

i- ^q^ = E E и k ( x ³ J q ^a “ ² k ( ^z ) d a d a • (В6) k d x       k

i d a k dx³ ₍ b'

a,a ₂ s '

! aa .

=к z

k

( 0

. з J A

( a ^m - ™ 2 ^k J

(В14)

Для дальнейших выкладок запишем оператор Гамильтона–Максвелла в виде

A

(В7)

Операторы A , B имеют вид

A = I X c ( £^{- 1} ( k ^{2 (}

- 1

л a “ 2 s _ "^Z1—— 2 k

^a 1 ^a 2 . ^u 01 — 2 k

где ( e “ - “ ^{2 -} s

B = ⁽ - 4 C (1) + £ ⁽ 0

( k 2          I- 1

(В8)

C ( г^{- 1}

( D 1 £^{- 1} D ₂ ; - D 1 £^{- 1} D 1 ; J

( D 2 ^ ¹ D 2 ; - D 2 ^ ¹ D 1 ;)

(В9)

где дифференциальные операторы D 1 , D 2 имеют вид D 1 = d / d x ¹, D ₂ = d / d x ², £ - распределение диэлек-

трической проницаемости.

В этом случае матричное дифференциальное уравнение разбивается на систему двух операторных дифференциальных уравнений с дифференциальными

матричными операторами, которые можно предста-

вить в виде матриц 2×2. Система уравнений имеет вид

i ^d E = AH LBHL k d x^{3 1} k d x³

= BE •

(В10)

Представим решение системы уравнений Максвелла в эволюционном виде линейной комбинации двумерных базисных векторов (ранее для описания использовались четырёхмерные вектора )

I E ) = £ Г a ““ 2 s I x ³JI e _aa Jd²a _-:           I ) ^a 1 ^a 2 - s/

s

I H = Ej b ""[ x ¹ )| e ,„- . ) da s

(В11)

где d² “ = d “ 1 d “ ₂.

Решение будем искать в представлении, в котором базисные вектора имеют вид

e_aa i = Q_aa , exp I ik I a x 1 + “ x 2 )l - “ 1 “ 2 i “ 1 “ 2 i                ( 1             2      ) 1

J

Q ^ = W Г a^1- Q ^ = W Г

( ^a 2 J                     (

W (“)ll = k'

(В12)

(В13)

Скалярное произведение базисных векторов представляется через сингулярную функцию Дирака

J e—i I e ““ 2 i ) $ ⁽® 1 ^a 1 -^— 2 “ 2 ) •

Подставляем это разложение в систему уравнений Максвелла, получаем систему обыкновенных интегро-дифференциальных уравнений

B “a ^s I x ³ J

( ш1ш2 k ()

/ aja2 - 8Д\

\^{e     Ae} m,— , k /-

“ aja2 - sj>\

\^e    Be — k /,

)

b ш , — k

d² “-

(В15)

I - вектор, сопряжённый к вектору | e _{a a},_v .

В результате решение системы уравнений Максвелла сводится к решению системы обыкновенных дифференциальных уравнений. В случае, если ди-

электрическая проницаемость среды не зависит от продольной координаты, система дифференциальных уравнений превращается в систему дифференциальных уравнений с постоянными коэффициентами.

Приложение Г. Алгоритм решения задачи прохождения через периодическую структуру с дефектом для ТМ-поляризации

Запишем явные выражения для матриц в случае ТМ-поляризации

A 1

B 1

C 1

D 1 =

T .

(. £

I ^£ 2

( ^£ 2

( ^Y 1 ₍ £ 1

^-Y 1 J ( exp ( ik Y 1 d 1 ) 0 J £ 1 ) (       0         1 ) ^-

^-Y 2 ll ¹         ,⁰ j,

£ 2 ) ( 0 exp ( ik у ₂ d ₂ ) )

-Y ₂ J ( exp ( ik Y ₂ d ₂ ) 0 J

£ 21     0        1 )^-

^-Y 1 ^{1       0}

£ 1 ) ( 0 exp ( ik Y 1 d 1 ) ) ,

Q 1 = и 1 R 1 ,

U 1 = D 1 ^{- 1} C 1 - R 1 = B 1 ^{- 1} A 1 ,

B 2 =

^Y 2

( £ 2

(

^Y 1

₍ £ 1

C 2 =

D 2

^Y 1

₍ £ 1

^Y 2

( ^£ 2

^-Y 2 J ( exp ( ik Y 2 d 2 )

£21     0

1          A

^-Y 1 ^{1       0}

£ 1 ) ( 0 exp ( ik Y 1 d 1 ) ) ,

^-Y 1 J ( exp ( ik Y 1 d 1 ) 0 J £ 1 1      0        1 ^{J -}

1           A

^-Y 2 ^{1       0}

£ 2 ) ( 0 exp ( ik y ₂ d ₂ ) ) ,

Q 2 = и 1 R 1 ,

U ₂ = D ₂ ^{- 1} C ₂ - R ₂ = B ₂ ^{- 1} A 2 .

Сшивка на дефекте имеет вид

A = ( Y 2 ^-Y 2 J ( exp ( ik Y 2 d 2 ) 0 J

^Л I £ 2 £ 2 ) (      0        1 ) ,

B 0 =

^Y 0

( ^£ 0

^-Y 0

£ _{0 )}

exp ( ik Y ₀ d )

(Г1)

(Г2)

(Г3)

(Г4)

(Г5)

(Г6)

C = 0	Y 0	"Y ° 1	। exp ( ik Y 0 d )	0 1
	e 0	e 0 1	к 0	1
Dn =	' Y 2	-Y2'	1 1           0
0	^ e 2	e 2 .	0 exp ( ik y 2 d 2 )

S = U 0 R 0 F 2 N , U 0 = D o - ¹ C 0 ’ R 0 = B 0 - 1 A o .

(Г7)

(Г8)

(Г9)

Сшивка на первом и последнем слое приводит к решению системы уравнений

Y Y I

A             = N F,

0*0 I    I T^VMM I      II r'TM¹ 1 ,

кe) к-e I)

T

TM

Y e

M TM S 2 N ’

N

TM

M TM

^Y . e 1 I Y i I e 1

^-Y 1 1        ⁰

e ] [ 0 exp ( ik Y d 1 ) ) ’

^-Y 1 । exp ( ik Y 1 d 1 )

e JI 0

(Г10)

(Г11)

(Г12)

(Г13)

Связь коэффициентов на первом и последнем слое

F2 n = RQN-1F1,(Г14)

^S 1 = ^U 0 ^R 0 ^F2 N ,

  _ p n^{N -1} e

S2N = R2Q2

(Г15)

(Г16)

Исключая ненужные переменные, получаем s2 n = R 2 Q2N-1u0 R 0 R1Q1N-1F1.(Г17)

Система уравнений для определения коэффициен- тов пропускания и отражения

I    y)Y))

I A0I I-RTmI    II = NtmF1,(Г e -e

Y

Ггм\ I = MtmR2Q2N-1U0R0R1Q1N-1F1.(Г19)

( e )

Эта система содержит четыре уравнения и четыре неизвестных.

Параметры для тестирования программы

4 n ₁ d ₁ 1 4 n ₂ d ₂ 1 2 n ₀ d 1

= ’^T = ’    = ,

λ 0 – длина волны, на которой должен быть максимум пропускания фильтра. В этом случае коэффициент пропускания равен 1.

Проверочный тест для вычисления коэффициентов отражения и пропускания

I R tm I²+ T Tm I²=KI²,

I R te Г + T te Г = B 0|².