Моделирование гиперспектрометра на спектральных фильтрах с линейно-изменяющимися параметрами с использованием векторных бесселевых пучков

До появления видеоспектрометров спектры отражения и излучения поверхности Земли мало использовались в качестве идентификационных признаков, хотя изучались десятки лет и были хорошо известны [1 –4]. Это было связано с тем, что авиационные спектрометры имели низкое геометрическое разрешение, давали информацию только вдоль линии полёта и позволяли судить о спектральных свойствах лишь достаточно протяжённых объектов. В результате видеоспектральной съёмки формируется многомерное пространственно-спектральное изображение, в котором каждый элементарный участок изображения – «пиксел» – характеризуется собственным спектром. Такое изображение носит название «куба» информации, два измерения которого соответствуют пространственному изображению местности на плоскости, а третье – характеризует спектральные свойства изображения. Спектральное разрешение современных видеоспектрометров достигает 1,8–2,0 нм и обеспечивает построение спектральных характеристик подстилающей поверхности, определяемой мгновенным полем зрения прибора (для авиационных видеоспектрометров – около 1 мрад [5, 6]).

Для решения конкретных задач используются гиперспектрометры различных типов – дисперсионные, интерференционные и фильтровые.

В данной работе рассмотрен гиперспектрометр, основанный на применении спектральных фильтров [7]. Гиперспектрометры содержат в конструкции фильтры с изменяемыми по апертуре спектральными характеристиками [8– 11].

В случае использования в гиперспектрометре фильтров каждая точка изображения проходит множество светофильтров. Для того чтобы восстановить гиперспектральное изображение, требуется найти функцию рассеяния точки для каждого спектрального фильтра. Для этого необходимо разработать методы моделирования фильтрового гиперспектрометра.

Предметом данной работы является моделирование гиперспектрального блока с использованием векторных Бесселевых пучков. Это позволяет ускорить время моделирования примерно на порядок.

1. Решение задачи о прохождении электромагнитных волн через слоистые структуры на основе разложения по каноническим бездифракционным ТМ- и ТЕ-поляризованным пучкам

Во многих оптических приложениях необходимо решать задачу прохождения бездифракционной волны через металлический или диэлектрический слой. Бездифракционные (самовоспроизводящиеся) волновые пучки обладают общим интересным свойством: при распространении в свободном пространстве у них изменяется только фаза, но не изменяется распределение комплексной амплитуды. Некоторые безди-фракционные пучки обладают ещё одним замечательным свойством: они представляются в виде функции с разделяющимися переменными. Будем называть без-дифракционные пучки с разделяющимися переменными каноническими бездифракционными пучками.

Система уравнений Максвелла в цилиндрических

координатах относительно поперечных компонент электрического и магнитного поля имеет вид:

i d w k d x³

= H W \ H =

¹ I B

A

где

A = -1 c ( e f x ¹11 -o, B = - -1 C ( 1 ) + e f x ¹1 o,      (2)

k ²                              k ^{2 v 7}     ^ ¹

C f e f x ¹ 11 =

o =

De ^f x ¹ 1 D 2 ;

e f x ¹ 1 D 2 D 2 ;

^- De ^f x ¹ 1 D 1 ^;

e f x ¹ 1 D 2 D 1 ; ^

f 0 1 1

I- 1 0 J ’

D i =

D 2 =

1 ' x x¹ d x¹

1 a x1 dx2’

=7⁺ D ,

e ^f x ^{1 7} = e ^{1 f} x ¹ 7 ,

где x 1 –радиальная координата, x 2 –угловая переменная.

В цилиндрических координатах бездифракцион-ные пучки имеют следующий вид

W ( xⁱ, x ², x ³ ) = w (.

x ¹, x ² ) exp f ik Y x ³ 7 ,

^

= Js ( Y ( e0 ,a) ei,a, m ( x1, x 2 ) , - e2>a> m (x1, x2) ) X 0m f A (a,m)7                 ;

x ,     ' exp l ik y e„,a x I d a .

2 B ₀ ( a , m ) 7     ^{2 ( 0} ’ ) ⁷

При x ³ =0:

W M ( x ⁱ, x ², x ³ ) =

Y e i, a , m ( x 1 , x 2 )

^e e 2,a,m ( x ⁱ, x 2 )

f

W E ( x ⁱ, x ², x ³ ) =

2 f

^- e 2, a , m ( x ⁱ, x ² ) Y e i. a , m ( x¹, x ² ) 7

3) exp I ik Y x I ,

3, exp I ik Y x I ,

^

= J S ( Y(e0,a) ei,a,m (x1, x2 ) , - e2,a,m (x*, x2 )) X 0m x I A3 (a, m) 7 da.

2 B ₀ ( a , m ) 7

^e i, a , m ( x ⁱ, x 2 ) =

2 x

f

e 2, a , m ( x ⁱ, x 2 ) =

exp ( imx ² ) ,

Далее, используя соотношение ортогональности для функций Бесселя, получаем коэффициенты раз ложения A0(a,m), B0(a,m) по ТЕ- и ТМ-волнам.

После прохождения слоистой среды компоненты электрического поля имеют вид:

im т f,~ _.i 7

1 Jm I k a n 2 x J x 2         7

J m ^{f k a} n 2 ^{x 1} 7 _ч о x    ^{2         7}

exp ( imx ² ) ,

'A (^a , m ) 7 = I T tm 0 V A , ( ^a , m )' B 2 a , m 7^J"2 0 T _TE 7 2 B 0 2 a , m 7,

где Y — постоянная распространения бездифракцион-

ного пучка, e - диэлектрическая проницаемость, J_m ( x ) – цилиндрические функции Бесселя, x ¹ , x ² , x ³ – цилиндрические координаты.

Пучки W TM называются пучками поперечно-магнитного типа. Они не имеют продольной составляющей магнитного поля. Пучки W TE называются пучками поперечно-электрического типа. Они не имеют продольной составляющей электрического поля.

Рассмотрим разложение результирующего поля в виде суперпозиции бездифракционных ТМ- и ТЕ-по-ляризованных пучков. Формальная теория представления решения системы уравнений Максвелла в виде суперпозиции бездифракционных пучков изложена в Приложениях A и B. В однородной среде выражение для пучков имеет вид:

W _TM ( x^T, x 2 , x ³ ) =

Объединяя формулы, получаем выражение для компонент электрического поля после прохождения слоистой структуры

E ^f x ^t , x ² , x ^{3 7} =

^

J s ( Y (^e 0 ^,a) ^e i, a , m ( x ¹, ^{x 2} ) , ^{- e} 2, a , m ( x ', x 2 ) ) ^{X        (i5)}

0 ^m

f A ( a , m ) _X

2 B ( a , m )

exp 2 ik Y ( e ₀ ,a ) x ³ 7 d a .

Приведённая формула в дальнейшем будет использована для моделирования пятна рассеяния точки при прохождении спектрального фильтра.

где

Y(e0,a) ei,a, m (x, x ) f ,              ,7

= i 1 2\     exp I ik f Y(e0,a) x II’ e0e2,a,m ( x, x)            1 277

WTE (x \ x 2, x3) = e0e2,a, m (x , x )    ] f ,             з (ii)

= ,       3       ( !       exp I i^{k f} Y ^(e 0 ^{,a) x} 7J ’

2Y(e0,a) ei,a,m (x,x )7     27

Y ( e 0 ,a ) = ^0 -a ² .

Рассмотрим только компоненты электрического поля

2. Расчёт коэффициента отражения и пропускания на квазипериодической системе диэлектрической системы слоёв

В данном разделе рассмотрено распространение волны в структуре, представляющей систему слоёв с диэлектрическими проницаемости e _t , e ₂ и толщинами d ₁, d ₂ соответственно. В середине структуры находится дефект, представляющий собой слой с диэлектрической проницаемостью e ₀ и толщиной d ₀. Первый и последний слои имеют диэлектрическую проницаемость e _i. Непосредственно к дефекту прилегает слой с диэлектрической проницаемостью e 2 .

Для случая плоских волн базовые методы изложены в работах [12– 14]. В данной работе приведены методы, инвариантные к выбору бездифракционных пучков. Однако, несмотря на этот факт, все формулы в данной работе будем приводить в цилиндрической системе координат.

Решение в однородной среде

В случае ТМ-поляризации решение системы уравнений Максвелла представляется в виде

W _TM ( x 1 , x ², x ³ ) =

a TM V ^a , x ^J e 1, a , m ( x , x ) ^b TM | “’ x 3 J e 2, a , m ( x 1 , x 2 ) ,

3. Прохождение векторной Бесселевой волны через спектральный фильтр

Рассмотрим прохождение векторной Бесселевой волны через спектральный фильтр, изображённый на рис. 1, со следующими параметрами: e 1 = 2,25; e ₂ = 6,25; e d = 1; d 1 = % ₀/6 - толщина слоя с e 1 ; d ₂ = 0,1 A o — толщина слоя с e ₂; d = 0,5 X q - толщина слоя с e d ; X q = 1 мкм.

Подставляя это свелла, получаем,

представление в уравнения Мак-что уравнение для функций

a _TM( a , x 3 ), b _TM( a , x 3 ) в однородной среде с диэлектрической проницаемостью ε имеет вид

i_ d | a _TM ( a, x ³) k d x ³ V b _TM ( a, x 3 )

I

^^^^^^e

V

0 e^{- 1} y ² ( e,a )Y a TM ( a, x 3 )'

I ^e где y ( e,a ) = TE

^^^^^^e

J V b TM ( a, x 3 ) f a 1 ² - a 2 .

Решение в однородной среде с проницаемостью ε имеет вид

диэлектрической

Увеличение числа периодов N , используемых в спектральном фильтре, приводит к сужению полосы пропускания длин волн. Как видно из рис. 2, с увеличением числа слоёв запрещённая зона вокруг базовой длины волны Х ₀ = 1 мкм становится более выраженной, и ширина полосы пропускания стремится к нулю.

I

. 3l)

a TM ^{( a} , x )

V ^b TM ^{( a} , x ^{3 )} J

= G ( e,a ) U V e,a, x 0 , x 1

, x ³

c

C ^-

V 1 J

,

G ( e,a ) = ( g i ( e,a ) g 2 ( e,a ) ) , f y ( e,a ) )            f-y ( e,a )

g 1 ( e,a ) = l          I, g 2 ( e,a ) = l

v e V             v e

U [ e,a, x ₀ , x 1 , x ³ ) =

,

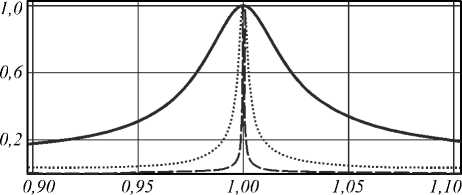
Рис. 2. Зависимость коэффициента пропускания спектрального фильтра от длины волны для нулевой частоты при N=3 (сплошная линия), N=5 (точечная линия), N=7 (пунктирная линия)

Если параметр в Бесселевом пучке, падающем на спектральный фильтр, будет возрастать, то пик пропускания будет смещаться. Причём смещение для TE-и ТМ-поляризации будет различным [15]. На рис. 3 показаны графики пропускания рассматриваемой структуры ( N =7) в зависимости от длины волны для

exp ^ ik y ( e, a ) ^ x ³ - x ₀

V

exp V - ik y ( e,a ) V x ³

^^^^^^e

.

V

В случае ТЕ-поляризации решение системы уравнений Максвелла представляется в виде

I

W _TE ( x 1 , x ², x ³ ) =

(        3 )                   1 ..2

a TE V ^a , x J e 2, a , m ( x , x )

)

bTM

( ^a , x 3 ) e 1, a , m ( x 1 , x 2 ) /

Уравнение для функций a m ( a , x 3 ), b_m ( a , x 3 ) в однородной среде имеет вид

i d [ a _TE ( a, x ³) J = _ef    0

k d x ³ V b _TE ( a, x 3 ) J     VY 2 (^e ,a )

¹ ) a TE ( a, x )

0I b ( a, x 3 )

/ V TE ' ’     ' V

. (21)

Решение в однородной среде с диэлектрической проницаемостью ε 1 имеет вид, аналогичный виду для

ТМ-поляризации. Однако матрица G (e 1 , a ) имеет вид

G ( e,a ) = ( g 1 ( e,a ) g 2 ( e,a ) ) ,

g_x ( e,a ) = I      ¹ I, g ₂ ( e,a ) = I 1 I .      (22)

V Y ( e,a ) J            V-Y ( e,a ) J

Полученные уравнения полностью совпадают с уравнениями в работе [15], поэтому для прохождения векторных Бесселевых мод через спектральный фильтр будем использовать алгоритм, приведённый в работе [15].

излучения, для Бесселевого пучка с числовой аперту-

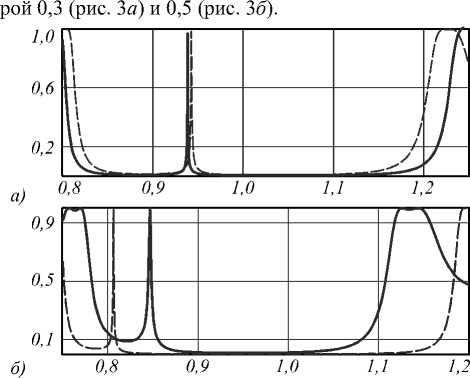
Рис. 3. Зависимость коэффициентов пропускания спектрального фильтра от длины волны для TE-(пунктирная линия) и ТМ- (сплошная линия) поляризации при числовой апертуре конической волны 0,3 (а) и 0,5 (б)

Хорошо видно, что происходит значительное смещение центрального пика, а также различие картины для TE- и ТМ-поляризации. Данный факт свидетельствует о том, что при использовании спектрального фильтра в короткофокусной оптической системе (лучи идут под большими углами к оптической оси) будет происходить искажение пятна рассеяния и, соответственно, изображения.

4. Фокусировка Гауссова пучка через спектральный фильтр

Рассмотрим прохождение линейно-поляризованного Гауссова пучка со сферическим волновым фронтом через спектральный фильтр. Рассмотрим случай, когда спектральный фильтр расположен в области изображения объекта, который в нашем случае представляет точку, излучающую немонохроматический пучок. В этом случае фильтр расположен в окрестности фокуса сферического пучка. Для расчётов будем использовать локальное приближение, которое заключается в том, что характеристики спектрального фильтра слабо изменяются в окрестности пятна рассеяния. Это позволяет нам свести решение задачи о прохождении Гауссова пучка со сферическим волновым фронтом через фильтр с линейно-изменяющимися параметрами к задаче о дифракции на квазипериодической системе слоёв, которая была рассмотрена разделе 2. Решение задачи будем проводить в цилиндрической системе координат, так как в случае центрированной оптической системы излучение, падающее на фильтр, легче представлять в виде векторных Бесселевых пучков, чем в виде суперпозиции плоских волн.

На рис. 4 и 5 показаны результаты моделирования фокусировки (квадрат модуля электрического поля) Гауссова пучка с базовой длиной волны Х 0 = 1 мкм радиусом 8 мкм с различной числовой апертурой в свободном пространстве и при наличии спектрального фильтра с N =7.

На рис. 4 показаны результаты моделирования для числовой апертуры NA=0,08: при наличии фильтра происходит уширение спектрального пятна в 1,8 раза и падение интенсивности в 18 раз. Такое падение интенсивности связано со смещением пропускаемой длины волны. На рис. 5 рассмотрена более острая фокусировка с числовой апертурой NA=0,4. В этом случае при наличии такого же фильтра происходит уширение спектрального пятна лишь в 2 раза, но падение интенсивности становится ещё большим.

Как видно из приведённых результатов, с увеличением числовой апертуры (остроты фокусировки) при использовании спектрального фильтра происходят всё большие потери энергии, связанные с блокировкой лучей, идущих под большими углами к оптической оси. Также наблюдается уширение размера фокального пятна по сравнению с фокусировкой в свободном пространстве.

Заметим, что потери энергии в данном случае являются более значительными, чем уширение фокального пятна. Полученные результаты аналогичны результатам, полученным в работе [15], где расчёт проводился с использованием разложения по плоским волнам. Это свидетельствует о правильности проведённых расчётов.

Заключение

В работе получены результаты моделирования, позволяющие оценить возможность использования гиперспектрометра со спектральным фильтром с линейно-изменяющимися параметрами. В дальнейшем теория, приведённая в данной работе, будет использована для расчётов характеристик гиперспектрометров, используемых для дистанционного зондирования Земли.

Работа выполнена за счёт гранта Российского научного фонда (РНФ) № 14-31-00014.

Рис. 4. Распределение интенсивности (негатив) в плоскости фокуса для NA=0,08 (радиус области 10 мкм): в свободном пространстве (а) и при наличии спектрального фильтра (б)

б)

Приложение A

Пусть имеются базисные вектора

e 1, a , m

СaJ, (k ar) a "r mJ. (kar)

V r 7

e 2, a , m

im

- — J. ( k a r ) Г d J, (k a r)

V     d r      J

. (A1)

Рис. 5. Распределение интенсивности (негатив)

б)

Докажем ортогональность базисных векторов первого типа e e1,a, me1,p, m^

-Г r C ■'      ■     / " + 4 J . ( к a r ) J . ( k e r ) 1 d r = (A ² )

J 0 V dr        dr      rJ

-        C 1d С dJm (k ar) 1 .2

= ^{- rJ}m ( ^k P ^r )       \ ^r ----5----- I T ^Jm ( ^{k a r} ) d r .

J0           V r dr V dr J rJ

Учитывая уравнение Бесселя,

в плоскости фокуса для NA=0,4 (радиус области 5 мкм): в свободном пространстве (а) и при наличии

спектрального фильтра (б)

1 d \ rdJ_m ( ar ) r d r I      d r

^- ^rJ™ ( ar ) = ^- a²J m ( ^ar ) .   (A3)

r ²

Получаем, что скалярное произведение двух базисных векторов равно

\e1,a,m e l,^,m /

”

= k² a ² J 0 rJ _m ( k P r ) J _m ( k a r ) d r = a5 ( P-a ) .

(A4)

Учитывая ортогональность функций Бесселя , по лучаем ортогональность базисных векторов .

Ортогональность базисных векторов второго типа доказывается аналогично.

Докажем также ортогональность векторов различ- ных типов

' 1,a, me2,в, m f ~ (im dJ (к “r)

= J „ rl--5-----Jm (k P r) + j о i r       dr im

■     ^J m ( ^k “ r )

r

d J m ( k P r ) L

-------------I d r d r J

(A5)

“ d

= f„ im 3"( ^J m ( ^k “ r ) ^J m ( ^k P r )) ^d r = 0.

J ⁰ d r

Приложение В

Разложение электрического поля по векторным Бесселевым пучкам описывается выражением:

^

E ( p , ф , z ) = ^ exp( im ф ) x m =-^

^

^;J( A “’ m e i,a, m ( p , ф ) ^{+ B} “’ m e 2,a, m ( p , ф ) ) ^exP ( ^ik Y ^{( a )} z ) ^d “ .

Коэффициенты разложения имеют вид:

(B1)

A a , m

B a , m

= k JI e 1’ “ ’ m ( P , ф ) Е ( Р , Ф ,0) ^ex P( - im ф ) р d p d Ф ,

a

= — JJ e ^{2, a} , ^m ( p , ф ) Е ( р , ф , 0) exp( - im ф ) р d p d ф ,

( E_ ( p , ф ,0) )

где E(P•Ф•0) = IEф(p,ф,0)J ’ e1,a,m (p, ф) = f dJm (k“r), -imJm (kar)I, I      d r          r e 2,a, m

'mJ. (k “r) ’ dJmIk“r> rd

.

Для линейно-поляризованного пучка m ( Ex (P, ф,0)cOS ф E(p, Ф,0) = l r

(- Ex ( p , ф ,0)sin ф

.

(B3)