Моделирование ГПУ-циркония методом молекулярной динамики

Атомная энергетика активно развивается в последние десятилетия. Совершенствование технологий, конструкции и безопасности ядерных реакторов необходимо для дальнейшего ее развития. Однако без глубокого и детального изучения взаимодействия излучения с веществом это невозможно. Данные исследования позволят не только расширить представления о физической природе процессов, происходящих в материалах под облучением, но и предоставит возможности использования новых материалов и методов при конструировании ядерных реакторов, а также модернизировать уже имеющиеся реакторные установки.

Развитие вычислительных средств в последние годы позволяет рассматривать компьютерное моделирование как наиболее удобный и перспективный метод исследовани й в области реакторного материаловедения [1]. Вычислительный эксперимент позволяет детально изучать различные процессы, происходящие в материалах под облучением, в то время как проведение натурных экспериментов зачастую затруднено, а в ряде случаев – невозможно. Компьютерное моделирование основывается на теоретических основах происходящих процессов и позволяет изучать не только равновесное положение, но и динамику протекающих таких процессов.

Одним из основных методов вычислительного эксперимента, позволяющих исследовать процессы на уровне отдельных атомов, является метод молекулярной динамики (МД). Этот метод основывается на решении уравнений механики Ньютона для совокупности взаимодействующих атомов, образующих модельный кристаллит.

Настоящая работа посвящена МД-моделиро-ванию ГПУ циркония. Цирконий обладает удачным сочетанием ядерно-физических характеристик и механических свойств и потому считается одним из наиболее перспективных конструкционных материалов ядерных энергетических установок. В настоящее время сплавы циркония широко используются для изготовления оболочек топливных стержней и элементов конструкции тепловыделяющих сборок реакторов с водой под давлением.

В работе приводятся результаты расчетов энергий формирования дефектов кристаллической структуры, оценивается пороговая энергия смещения, моделируются каскады атомных смещений и подсчитываются количества пар Френкеля, переживших рекомбинацию в каскаде («выжившие» дефекты). Полученные в ходе расчетов результаты сопоставляются с имеющимися в литературе данными.

МЕТОД МОДЕЛИРОВАНИЯ

Для циркония в данной работе используется многотельный потенциал, предложенный Мен-делевым и Акландом в работах [2, 3]. В работе [3] авторами предлагается несколько потенциалов. Обозначенный ими как потенциал #3 используется для ГПУ-Zr, который и рассматривается в данной работе. В литературе отмечается [4, 5, 6], что данный потенциал является наиболее совершенным и дающим хорошее согласие с экспериментальными данными. Использование потенциала, приведенного в работе [2] сделано с целью сопоставления различия результатов моделирования и возможного выявления особенностей или недостатков модернизированного потенциала по отношению к его более ранней версии. Оба являются потенциалами вида Финни-са-Синклера [7].

Для проведения дальнейших расчетов использовалась модель кристаллита ГПУ-Zr, а также периодические граничные условия. Построение модели осуществлялось с помощью трансляционной симметрии, задав изначально координаты базовых точек. В зависимости от температуры варьировались параметры решетки.

ЭНЕРГИЯ ФОРМИРОВАНИЯ ТОЧЕЧНЫХ ДЕФЕКТОВ

При воздействии различных факторов (например, нагрев, облучение и т.п.), в кристаллитах могут образовываться точечные дефекты (нарушение трансляционной симметрии кристалла): вакансии и собственные междоузельные атомы (СМА). Используя методы компьютерного моделирования можно добавить или убрать один из атомов. Реализовать такое на практике не представляется возможным, однако для исследовательских целей такой метод не только прост, но и достаточно информативен.

В таблице 1 приведены результаты вычислительных экспериментов, описанных в работах [2, 8, 9]. Рассмотренные конфигурации СМА в ГПУ решетке циркония показаны на рис. 1.

Отсутствие данных по той или иной конфигурации объясняется тем, что такая конфигурация неустойчива и при релаксации она переходит в другую рассматриваемую конфигурацию, что так же отмечалось в указанных выше работах

ПОРОГОВАЯ ЭНЕРГИЯ СМЕЩЕНИЯ

При взаимодействии с материалом происходят упругие и неупругие столкновения бомбардирующих частиц с атомами. В результате таких столкновений часть энергии излучения передается атомам, которые называются первично выбитыми атомами (ПВА). Если переданная энергия оказывается достаточно большой, атом может сместиться из своего узла кристаллической решетки и образовать пару Френкеля (вакансия – междоузельный атом). Минимальная кинетическая энергия, необходимая для образования устойчивой пары Френкеля, называется пороговой энергией смещения.

В кристаллите выбирается ПВА, которому сообщается определенная энергия и направление движения. Устойчивой парой Френкеля в рамках данной работы считалась такая пара, которая не прорекомбинировала в течение 10 пикосекунд. Расчет проводился для четырех изотропных случайных направлений на двух потенциалах [2, 3]. Как было сказано выше, из работы [3] брался потенциал для ГПУ-Zr (#3). Для каждого рассматриваемого направления ПВА строился кристаллит своих размеров для избегания «зацикливания» возмущений вследствие периодических граничных условий.

Таблица 1. Энергии формирования вакансии и различных конфигураций СМА в ГПУ решетке циркония, эВ

Конфигурация	[2]	[8]	[9]
Вакансия	1.786	-	-
BC	3.756	3.24	-
BS	3.760	3.53	3.60
BO	3.970	3.24	3.53
C	3.979	3.56	-
S	4.319	3.44	4.57

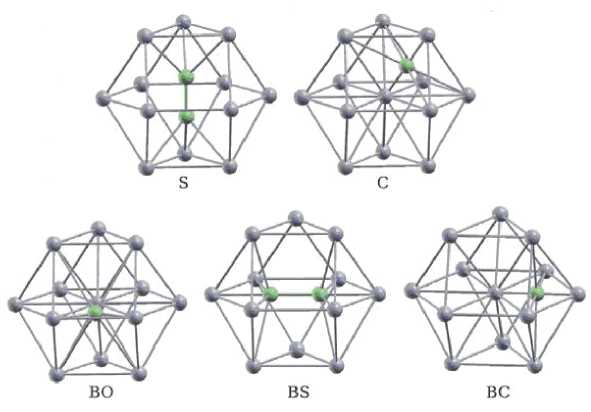
Рис. 1. Конфигурации собственного СМА в ГПУ решетке циркония

Количество атомов в кристаллите варьировалось от 12 до 24 тысяч в зависимости от условий вычислительного эксперимента.

Для нахождения пороговой энергии проводилась серия экспериментов с шаговым увеличением энергии ПВА на 1 эВ. Как только удавалось получить пару Френкеля, которая не прореком-бинировала в течение 10 пикосекунд, данная энергия ПВА фиксировалась. Ввиду того, что даже превысив пороговую энергию, можно получить ситуацию, где пара Френекеля прорекомбениро-вала быстрее, шаговый метод является более достоверным, исключая ошибку перескока. Резуль- таты моделирования приведены в табл. 2.

Пороговая энергия сильно зависит от выбранного кристаллографического направления, что определяется кристаллическим строением.

КАСКАДЫ СМЕЩЕНИЙ

При сообщении некоторому атому достаточно большой энергии инициируется каскад атомных смещений. Размер каскадной области определяется энергией ПВА. На рис. 2 представлен пример эволюции дефектной структуры кристаллита Zr при похождении каскада с энергией 5 кэВ.

Таблица 2. Пороговая энергия смещения

Направление ПВА	<0001>		< 1 2 10 >		< 1 1 00 >		< 0 1 10 >
Потенциал	[2]	[3]	[2]	[3]	[2]	[3]	[2]	[3]
Пороговая E, eV	50	63	34	34	65	77	119	124

Рис. 2. Эволюция дефектной структуры кристаллита при развитии каскада смещений: а – 0,09 ps; b – 0.26 пс; c – 0,65 пс; d – 3,85 пс; e – 7,52 пс; f – 44.84 пс Синие – вакансии, черные – междоузельные атомы

a)

b)

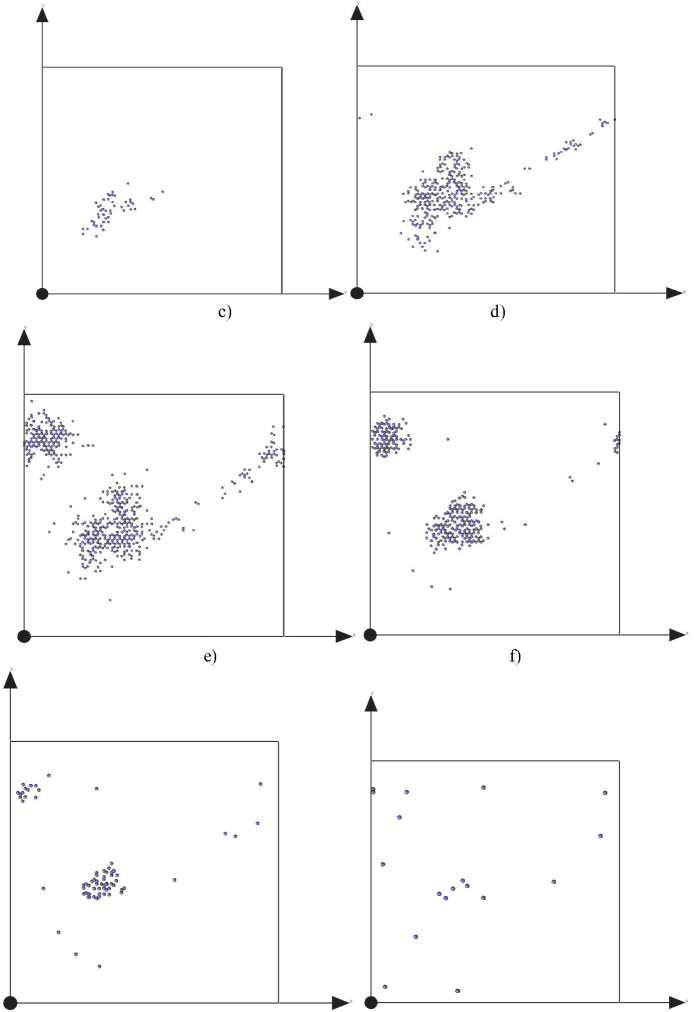
Пик каскада, завещающий так называемую баллистическую стадию, приходится на 0,65 пикосекунд. Миновав его, начинается процесс ре-комбенации точечных дефектов, по окончанию которого остается относительно небольшое количество дефектов («выжившие»дефекты).

В ходе экспериментов в данной работе использовались периодические граничные условия. Исходя из этого размеры кристаллита, а также энергия ПВА подбиралась так, чтобы не возник эффект наложения каскада на самого себя, что означало бы получение заведомо неверных данных.

Случайным образом определялось 8 направлений для ПВА. Расчет проводился для 1, 5, 10, 15 и 20 кэВ с размерами кристаллита ~100, 200, 300, 400, 500 тысяч атомов соответственно. Для расчета использовался потенциал из работы [3]. Результаты представлены в таблице 3, где ф и 0 это углы в сферической системе координат, определяющие направление движения ПВА: ф -угол, отсчитываемый от направления <1210 > в плоскости (0001), 0 - угол, отсчитываемый от направления <0001>, E – энергия ПВА, N – количество атомов Zr в модели кристаллита, t – моделируемое время каскада. Перед моделированием каскада кристалл релаксировали при тем- пературе 600 К и нулевом давлении в течение 10 пс. Указанные в табл. 3 и далее погрешности являются статистическими погрешностями, соответствующими одному стандартному отклонению для выборочного среднего (1 ^ ). Также был произведен расчет эффективности каскада по NRT-стандарту.

Также были проведены расчеты с помощью потенциала из работы [2] для энергий ПВА 15 и 20 кэВ соответственно при той же температуре. Полученные результаты представлены в табл. 4.

Полученные результаты показывают, что из общего числа атомных смещений от ПВА с энергией от 10 до 20 кэВ выживает 15-18% дефектов при работе с потенциалом [3] и 18-20% при использовании потенциала [2].

Изучения влияния температуры на количество выживших дефектов проводилось в работах [4, 10]. Отмечалось, что с ее ростом количество дефектов не изменялось в пределах погрешности. Проведенные исследования в рамках данной работы в диапазоне температур от 100 до 400 К согласуются с полученными ранее данными. Соответствующие результаты приведены в табл. 5. Для расчетов использовался потенциал из работы [3], и энергия ПВА 10 keV. В табл. 6 указаны

Таблица 3. Количество выживших дефектов

Направление	E = 1 keV N= 104832 t=23 ps	E = 5 keV N=209880 t=36 ps	E= 10keV N=296888 t=45 ps	E=15 keV N=405080 t=70 ps	E=20keV N=492800 t=88 ps
φ = 43.31 4 θ = 70.999	4	9	4	27	29
φ = 74.023 θ = 71.563	4	13	18	40	25
φ = 48.309 θ = 59.019	4	6	16	27	54
φ = 61.289 θ = 30.179	3	6	10	9	40
φ = 67.271 θ = 82.287	1	2	30	22	71
φ = 60.42 θ = 54.605	3	6	26	47	3
φ = 66.783 θ = 62.429	3	6	11	24	9
φ = 50.196 θ = 41.611	2	7	8	21	35
Среднее	3±0.378	6.875±1,109	15,375±3,179	27,125±4,147	33,25±7.898
ρ	0.3±0.038	0.138±0.022	0.154±0.032	0.181±0.028	0.166±0.039

Таблица 4. Количество выживших дефектов

Направление	E = 15 keV, N = 405080, t=70 ps	E = 20 keV, N = 492800, t = 88 ps
φ = 43.31 4 θ = 70.999	39	41
φ = 74.023 θ = 71.563	29	34
φ = 48.309 θ = 59.019	25	35
φ = 61.289 θ = 30.179	35	42
φ = 67.271 θ = 82.287	38	30
φ = 60.42 θ = 54.605	19	34
φ = 66.783 θ = 62.429	27	35
φ = 50.196 θ = 41.611	36	36
Среднее	31±2.514	35.875±1.381
ρ	0.207±0.017	0.179±0.007

Таблица 5. Количество выживших дефектов при различных температурах

Направление	T = 100 K	T = 200 K	T = 300 K	T = 400 K
φ = 43.314 θ = 70.999	29	26	17	20
φ = 74.023 θ = 71.563	24	26	14	15
φ = 48.309 θ = 59.019	29	19	12	12
φ = 61.289 θ = 30.179	10	14	18	22
φ = 67.271 θ = 82.287	17	16	22	10
φ = 60.42 θ = 54.605	14	8	23	14
φ = 66.783 θ = 62.429	21	9	13	13
φ = 50.196 θ = 41.611	19	23	19	25
Среднее	20.375±2.405	17.625±2.514	17.25±1.436	16.375±1.880
ρ	0.203 ± 0.024	0.176 ± 0.025	0.172 ± 0.014	0.164 ± 0.019

Таблица 6. Параметры решетки при различных температурах

Температура Параметры решетки a, A c, A 100 K 3.232 5.170 200 K 3.230 5.173 300 K 3.230 5.176 400 K 3.230 5.178 параметры решетки при различных температурах, которые использовались для построения соответствующих кристаллитов. Параметры решетки были рассчитаны для каждой из рассматриваемых температур методом молекулярной статики при нулевом давлении. Процент выживших дефектов не превысил 20%.

Стоит отметить, что количество выживших дефектов зависит от параметров решетки кристаллита, т.е. зависит от напряжений в кристал- ле. Это – отдельный результат, который представляет интерес дальнейшего изучения.

ЗАКЛЮЧЕНИЕ

Кратко сформулируем основные результаты работы.

В работе дан краткий обзор особенностей применения метода молекулярной динамики для моделирования радиационного кристаллических структур.

Путем компьютерного моделирования каскадов атомных смещений методом молекулярной динамики вычислены значения пороговых энергий смещения циркония для различных кристаллографических направлений вылета ПВА.

Получены данные о количестве выживших дефектов при использовании двух разных потенциалов [2, 3]. Результаты хорошо согласуются с проведенными ранее расчетами, однако установлено, что для больших энергий ПВА потенциал [3] дает больший разброс. Количество выживших дефектов при энергиях ПВА 10-20 кэВ не превышало 20%.

Отсутствие зависимости выживших дефектов от температуры подтверждается серией проведенных расчетов в диапазоне температур от 100 до 400 K и хорошо согласуется с данными других работ [4, 10].

В дальнейшем планируется провести расчетные исследования влияния элементов внутренней структуры (границы зерен, выделения 2-х фаз и т.п.) циркония и сплавов на его основе на особенности процесса радиационного повреждения.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг.