Моделирование гравитационного поля сложной конфигурации

Астероидная и кометная опасность является общепризнанной реальной угрозой космического пространства, которая требует постоянного внимания со стороны мировой общественности. В настоящий момент остро стоит проблема разработки методов мониторинга и противодействия потенциально опасным объектам. Для моделирования возможных схем исследования и уничтожения астероидной и кометной опасности, требуется решить задачу моделирования гравитационного поля объекта, которое часто имеет сложную конфигурацию.

В силу принципа аддитивности гравитационных сил в нерелятивистской небесной механике понятие гравитационного потенциала распространяется на дискретные точечные распределения тяготеющих масс. Элементарное для малого числа точечных масс определение потенциала трансформируется в серьезную математическую задачу для сложно организованных протяженных тел, примером которых могут служить планеты. Теорию гравитационного потенциала, история которой восходит к работам Ньютона, Клеро, Лапласа и Лежандра, следует рассматривать как один из наиболее разработанных и мощных разделов математической физики, тесно связанный с соответствующими разделами математического анализа, теории поля, функционального анализа и теории специальных функций.

гравитационного поля:

• -    моделирование потенциала астероида в сферических функциях, используемое для описания гравитационных полей планет;

• -    модель гравитационного поля, образованная суперпозицией гравитационных полей двух условных тел различной массы, вращающихся относительно общего барицентра:

  U ( % , У , z ) = G

  
  

mm

— + —

R i R 2

R i = V ⁽ % - % 1⁾² + ⁽ y - У 1⁾² + ^{( z} - ^z 1⁾² ,     ⁽²⁾

R 2 = V ⁽ % - % 2^{)2 + (} У ^- У 2^{)2 + ( Z - Z} 2⁾² , (3) где m^ m ₂ - массы условных притягивающих центров, %_z -, y_z -, z i - соответствующие координаты притягивающих центров, G - гравитационная постоянная. Для удобства анализа результатов, получаемых в рамках данной модели, перейдем от декартовой барицентрической системы координат к сферической барицентрической системе координат. В качестве фундаментальной плоскости сферической системы координат пусть выступает плоскость эклиптики. Формулы перехода определим следующим образом:

% = r • sin X- cos ф

• < y = r • sin X • sin ф (4) z = r • cos X ,

где X - зенитный угол, ф - азимутальный угол, r - расстояние от барицентра системы до заданной точки пространства.

В качестве объекта анализа выберем астероид Эрос (433), физические характеристики , которого представлены в табл. 1 [1].

Расстояние между условными притягивающими центрами, определяется исходя из периода вращения астероида, по формуле полученной [3, с.22]:

d = 3 1G ⁽ m , + m , ) , (5)

V to

Таблица 1. Физические характеристики астероида Эрос

Геометрические размеры, км	34,4x11,2x11,2
Средний диаметр, км	16,8
Масса, кг	6,69 - 10 15
Период вращения, ч	5,27

Таким образом, модель астероида в задаче представляет собой гравитационное поле двух условных притягивающих центров с массами: 4,356 ^. 10¹⁵ кг, 2,334 ^. 10¹⁵ кг и вращающихся вокруг барицентра с угловой скоростью 5,6 ^. 10^–4 рад/сек. Точные значения масс были выбраны исходя из геометрии формы астероида.

На рис. 1 представлен астероид Эрос [1] и линии уровня гравитационного потенциала пред- полученные в результате использования лагаемой модели.

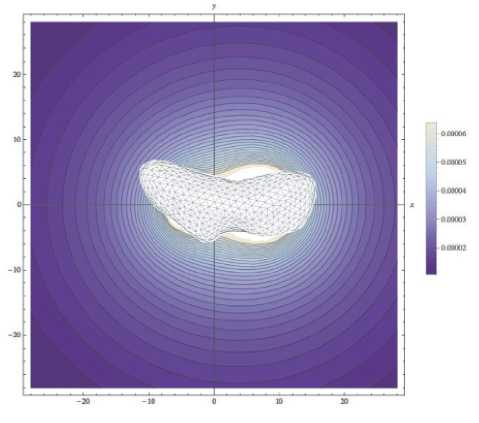
Рис. 1. Астероид EROS и линии уровня гравитационного потенциала, полученного в рамках предлагаемой модели

Для того, чтобы объективно исследовать точность предлагаемой математической модели, сравним ее с моделью гравитационного потенциала в сферических функциях, которая представлена в работе [2]. Определим выражение для гравитационного потенциала в сферических функциях:

Nn

= ^ 1 + УУ | a I r ^ ^ I r )

U r

I P” (sin ^ ) { c m cos m X + S_m sin m X } , (6)

где: r , Х , ф - сферические координаты точек;

• ц = GM -гравитационный параметр;

• a – средний радиус тела;

P _n ^m – присоединенные функции Лежандра степени n , порядка m ;

C m , S_m — сферические гармонические коэффициенты (определяются распределением масс астероида) [2], [4, с.36].

В случае когда определить сферические ко- эффициенты гравиметрическими методами затруднительно, согласно работе [2] предлагается определять сферические гармонические коэффициенты двумя методами: трех-координатным эллипсоидным приближением и методом многогранников. Ошибка при использовании трехкоординатного эллипсоидного метода составляет в среднем около 17,5%, но при расчёте коэффи- циентов методом многогранников погрешность снижается до 0,23% – рис. 2.

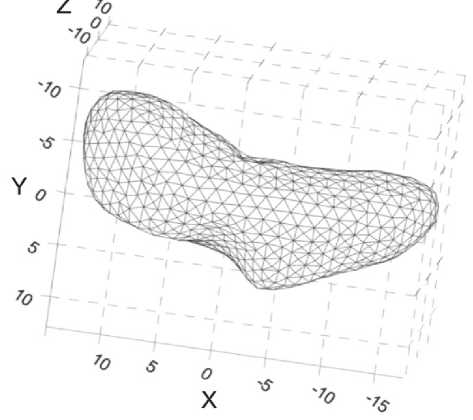
Рис. 2. Модель астероида Эрос (433), полученная при расчете сферических гармонических коэффициентов методом многогранников [2]

Проведем сравнительный анализ математических моделей гравитационного потенциала, полученного методом сферических функций и предлагаемым барицентрическим методом. Ограничимся четвертым порядком точности для зональных сферических функций и гармонических коэффициентов. На рис. 3 представлены кривые гравитационного потенциала, полученного в рамках предлагаемой модели и модели потенциала, полученного при его разложении по сферическим функциям при различных значениях аргументов. Таким образом, норма отклонения предлагаемой модели от модели потенциала в сферических функциях значительно уменьшается с увеличением расстояния от объекта моделирования, однако при этом, в зависимости от геометрии конкретного объекта, наблюдаются отклонения от реального гравитационного поля для различных значений углов широты и долготы.

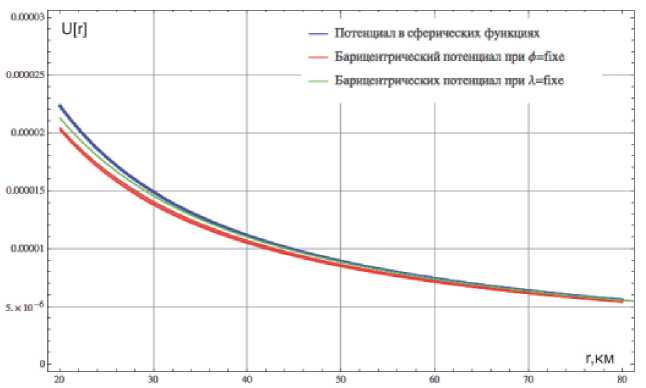
Рис. 3. Значения гравитационного потенциала при увеличении расстояния от барицентра до заданной точки для двух моделей потенциала

Из рис. 5 видно, что основное отклонение предлагаемой модели от модели гравитационного потенциала в сферических функциях наблюдается при предельных значениях широты ф е [0;2 п ] и среднем значении долготы Я е [0; п ] ; для прочих углов норма погрешности барицентрической модели минимальна. Таким образом, следует отметить, что сферические зональные функции создают более четкую картину в распределении потенциала в пространстве, что подтверждается более равномерным распределением значений потенциала (рис. 4). Однако расчетная максимальная погрешность в данном случае не превышает 10% (рис. 5). Очевидно, что при увеличении расстояния от барицентра системы до заданных точек пространства значение погрешности будет только уменьшаться.

Таким образом, исходя из полученных результатов, можно сделать вывод о том, что пред- лагаемая барицентрическая модель может быть использована при моделировании перелетов и маневров вблизи тел с гравитационным полем не сферической формы достаточно с высокой степенью точности. С увеличение расстояния модель все точнее отражает реальное положение вещей. Однако использование модели в каждом конкретном случает требует проведения дополнительных исследований, с целью выявить предельные отклонения от реальной картины гравитационного потенциала. Следует отметить, что полученная модель может применятся и при моделировании гравитационных полей космических объектов с более сложной геометрией, а количество притягивающих центров может варьироваться для обеспечения требуемой точности. Тогда задача моделирования перелета в гравитационном поле сложной конфигурации сводится к задаче перелета в системе n-тел.

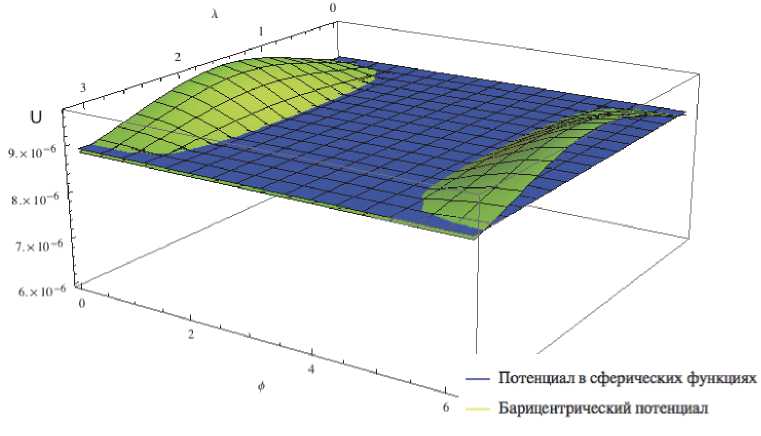
Рис. 4. Поверхности изменения гравитационного потенциала двух моделей при изменении значений широты и долготы при фиксированном значении расстояния от начала координат до заданной точки пространства ( r = 50 км)

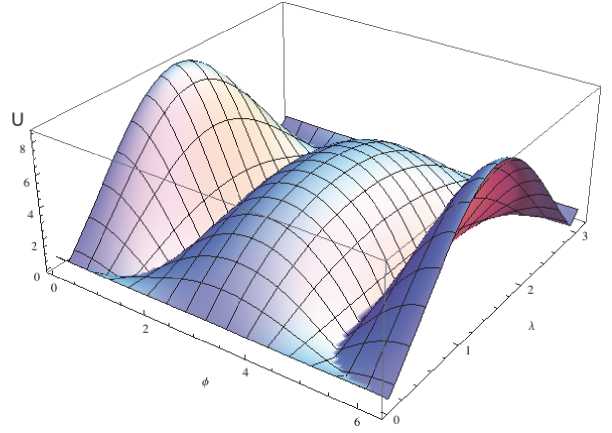
Рис. 5. Поверхность относительной погрешности для модели гравитационного потенциала с точечными притягивающими центрами (в %)