Моделирование химических реакций с использованием клеточных автоматов

Статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons «Attribution» («Атрибуция») 4.0 Всемирная (CC BY 4.0)

Множество физических и химических явлений принимают форму математических отношений. В физических системах взаимодействие параметров описывается с помощью математических уравнений, а в химических системах с использованием уравнений, которые задают взаимодействие ингредиентов и как они преобразуются при взаимодействии друг с другом.

Химической реакцией задается преобразование ингредиентов, а дифференциальные уравнения позволяют описать изменение объемов ингредиентов со временем в системе.

Использование клеточных автоматов позволяет смоделировать реальный химический процесс и пронаблюдать, как объем ингредиентов меняется со временем и на сколько это соотносится с результатами полученным при решении дифференциальных уравнений на концентрации ингредиентов.

В работе применяются следующие определения и обозначения.

• -    Агенты - исследуемые ингредиенты, занимающие ячейки на сетке.

• -    Ячейки - секции на сетке, в которых находятся агенты.

• -    Сетка - область, содержащая ячейки и агенты.

• -    Окрестность ячейки - область на сетке вокруг ячейки, которая изначально задается при моделирования клеточного автомата. Может задаваться по-разному окрестность фон Неймана, окрестность Мура).

• -    Правила - утверждения о действиях, которые будут предприняты агентами при определенных условия. Правила могут иметь вероятностную форму.

• -    Асинхронное применение правил - правила клеточных автоматов применяются к ячейкам в порядке с заданной изначально стратегией обновления клеток (случайный порядок, цикличный порядок и т. д.).

• -    Синхронное применение правил - заданные изначально правила для клеточного автомата одновременно применяются ко всем ячейкам на сетке.

• -    Гравитация - отношение между двумя агентами на сетке, по притяжению или отталкиванию.

• -    Движение на сетке - симуляция перемещения агента между ячейками на сетке. Перемещение достигается за счет исчезновения агента в одной ячейке и его появления в другой, соседней ячейке.

• -    Заглавными буквами обозначаются ингредиенты (A).

• -    Ингредиенты, заключенные в квадратные скобки, обозначают уровень концентрации вещества ([A] - концентрация A, то есть количество агентов в клеточном автомате со значением A).

• -    Клеточные автоматы в химии

Клеточные автоматы – это дискретные, агентно-ориентированные модели, которые могут быть использованы для симуляции сложных систем. Они состоят из: сетки ячеек, набора ингредиентов, называемых агентами, которые могут занимать ячейки, набора локальных правил, которые могут управлять поведением агентов, заданных начальных условий. Пример клеточного автомата на рис. 1.

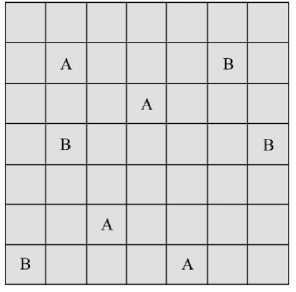
Рис. 1. Двумерный клеточный автомат с двумя агентами A и B

Особенностью клеточных автоматов является то, что не только агенты (ингредиенты) являются дискретными сущностями, но и пространство (ячейки) и время также являются дискретными, в противопоставление физическим моделям, использующим уравнения.

Сетки

Сетки могут быть одномерными, двумерными, трехмерными и так далее. Однако для визуализаций наиболее интересны двумерные и трехмерные сетки. Двумерные сетки классифицируются относительно замыканий границ: квадрат, цилиндр и тор. В квадрате ингредиенты встречают границы со всех сторон двумерной сетки. В цилиндре есть только верхняя и нижняя (левая и правая в зависимости от ориентации) границы. В торе границы не ограничивают движение агентов.

Клетки и ячейки

Клетки на сетке могут принимать различную форму: треугольные, квадратные, шестиугольные и другие. Каждая ячейка на сетке может существовать в различных, отличных друг от друга состояниях, что отождествляется с наличием ингредиента в ячейке.

Ячейка может быть пустой (нулевое состояние) или содержать определённый ингредиент (отличное от нуля состояние), представляя собой частицу, молекулу или изомер. Выбор формы ячейки зависит от сферы исследования. Все более популярными становятся ячейки, в которых каждая грань может взаимодействовать по своему собственному правилу. Такие ячейки называются неоднородными, пример таких ячеек можно увидеть на рис. 2.

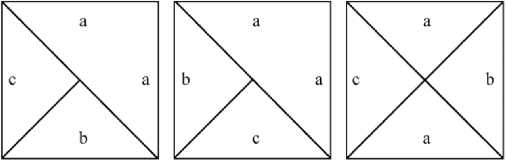
Рис. 2. Неоднородные ячейки клеточного автомата

Действия ингредиентов на сетке полагаются на правила, которые управляют их поведением при взаимодействии с ближайшими соседями.

Клетка и ее ближайшие соседи образуют окрестность клетки. Простейшей окрестностью клетки для двумерного автомата является окрестность Фон Неймана, пример на рис. 3. Другой распространённой окрестностью является окрестность Мура, которая также включает диагональные клетки, пример на рис. 4.

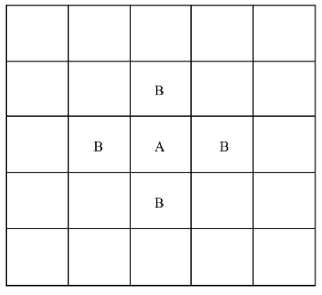
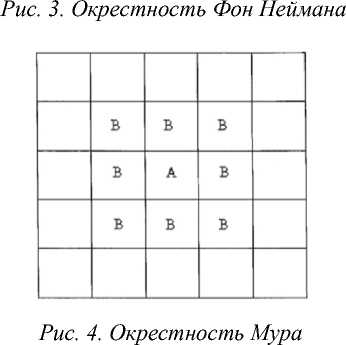
Правила

Несколько различных правил управляют поведением ингредиентов на сетке и, таким образом, последующей эволюцией клеточных систем [1]. Основными особенностями данных правил является то, что они:

• -    являются локальными;

• -    включают только сам ингредиент и возможно ингредиенты в его окрестности;

• -    единообразно применяются на протяжении всего исследования клеточного автомата;

• -    набор правил неизменен в течение работы клеточного автомата.

Правила движения

Динамика клеточных автоматов основывается на движении ингредиентов по сетке. Во время каждого шага по времени ингредиент имеет возможность переместиться вверх, вниз, влево или вправо в зависимости от установленных правил. При движении он может встречаться с другими ингредиентами и взаимодействовать с ними. В стохастических клеточных автоматах движение ингредиентов зависит от вероятностных правил перемещения ингредиента по сетке. P_m (A) определяет вероятность ингредиента A ячейки i перейти в одну из соседних незанятых другим ингредиентом ячеек j в окрестности ячейки i . Пример применения правила на рис. 5.

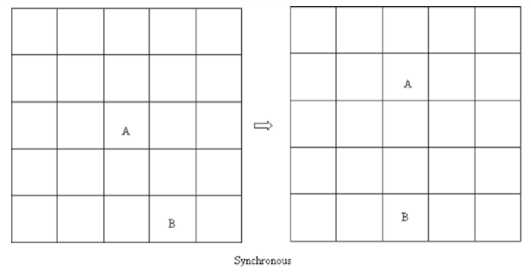
Рис. 5. Применение правила свободного движения

Правила соединения агентов

Определяет «склонность» движения ингредиента A к/от ингредиенту/а B , когда они разделены свободной ячейкой (ячейкой без ингредиента). Описывает притяжение или отталкивание ингредиентов между собой. Пример применения правила соединения на рис. 6.

• -    J - неотрицательное вещественное число.

• -    J = 1 вероятность движения в сторону B, как при его отсутствии.

• -    J >  вероятность движения в сторону B выше.

• -  0 <  J <  1 вероятность движения в сторону B ниже.

  

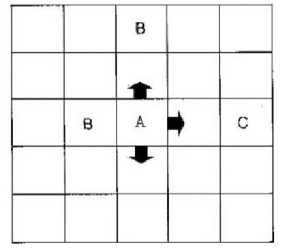
Рис. 6. Применение правила соединения. Ингредиент A может двигаться в три стороны в случае окрестности Фон Неймана

Правила разделения

Параметр Р ( ( Л В ) задает вероятность отделения ингредиента A от ингредиента B . Низкие значения вероятности означают сильную связность A и B , высокие значения - низкую связность. Если Р ( = 0, ингредиенты не разделяются друг с другом. Если Р ( = 1, у ингредиентов нет тенденции соединяться с друг другом.

Если молекула граничит с двумя молекулами и , то отделение устанавливается вероятностью Р((АВ ) * Р ( ( ЛС ) , если тремя, то вероятность пойти в соседнюю пустую клетку устанавливается Р ( ( ЛВ ) * Р ( (Л С ) * Р ( ( Л D ) . Если Л окружен четырьмя ингредиентами, то в случае окрестности Фон Неймана он не может двигаться. Пример применения правила разделения на рис. 7.

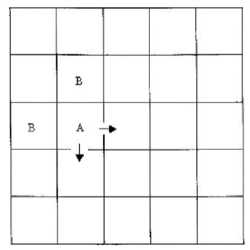
Рис. 7 Применение правила разделения агентов

Правила переходов

Задаются вероятностью перехода одного ингредиента в другой ингредиент P_t ( AB ) . То есть на каждой итерации работы клеточного автомата ингредиент A переходит в ингредиент В . При P_t ( AB ) =1, переход из A в В точно произойдёт. При P_t ( AB ) =0, переход из A в В не произойдёт никогда. Также на сетке могут устанавливаться более сложные переходы: P_t ( A + В → C + D ) =0․5, когда A и В встретятся на сетке (будут находиться в соседних клетках), они с заданной вероятностью перейдут в C и D .

Правила относительной гравитации

Параметр G_r ( AB ) в правиле перехода на цилиндрической сетке задает вероятность того, что если A находится над В , то A и В поменяются местами. Получится, что A со временем будет оседать вниз, а В подниматься вверх, то есть A соответствует более плотному материалу. Пример применения правила на рисунке 8.

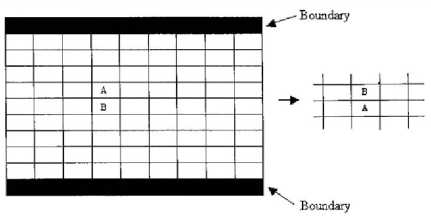
Рис. 8. Применение правила относительной гравитации

Правила абсолютной гравитации

Параметр G_a ( A ) показывает предпочтение движения в определенную сторону, например вниз, может обозначать тенденции движения для газов. При G_a ( A ) =0․2 ингредиенты A будут постепенно спускаться вниз.

Правила поворота ячеек

При использовании неоднородных ячеек следует учесть использование поворотов, так как это может повлиять на применение правил по граням. Чтобы достичь этого используются повороты на +90, -90, +180, -180 градусов во время каждой итерации. Только свободные ячейки поворачиваются, ячейки у которых в окрестности есть другие ингредиенты, не поворачиваются. Пример применения правила на рис. 9.

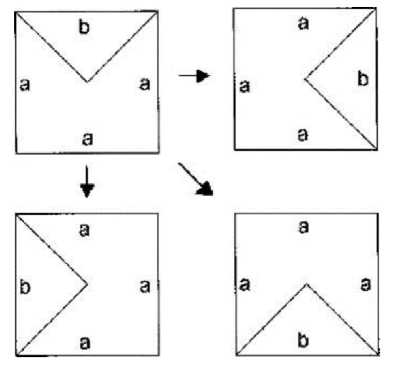
Рис. 9. Применение правила поворота неоднородных ячеек

Применение правил

Полная итерация клеточного автомата включает применение всех правил, которые возможно применить ко всем ингредиентам на сетке. Правила могут применяться синхронно и асинхронно. Синхронное применение правил может вызывать конфликты (например движение в одну клетку различных ингредиентов). В асинхронном применении ингредиенты выбираются в случайном порядке для применения правил.

Примеры: растворение, диффузия в воде, расслоение несмешивающихся жидкостей, кинетика возбужденных состояний атомов и молекул, энзимные реакции [2].

Химическая кинетика первого порядка

Многие естественные процессы такие как ядерный распад или мономолекулярные химические реакции являются представителями реакций первого порядка. Это значит, что такие процессы полагаются только на концентрацию веществ в первом порядке, то есть на преобразование самих ингредиентов. Клеточные автоматы для таких процессов принимают особенно простую форму. Правила движения ингредиентов в этом случае необязательны, достаточно использования правил переходов для самих ингредиентов.

Прототипом переходов первого порядка выступает распад А ^ В, то есть ингредиент А в каждую единицу времени переходит в В с вероятностью Р(АВ ) . При моделировании реакции с небольшим количеством А кривая концентрации довольно неровная и лишь примерно экспоненциальная, из-за случайных распадов, что является ожидаемым в столь ограниченной системе. Однако с повышением количества распадающихся ингредиентов кривая концентрации все ближе подходит к экспоненте, определяемой дифференциальным уравнением ^] = —/с[Л].

Если используется также правило перехода Р(В А) для перехода В ^ А, то моделируется обра тимая реакция вида А ^ В. В данном случае также ограниченные размеры системы вызывают замет- ные флуктуации значений концентрации ингредиентов на сетке (количество ячеек с ингредиентом)

_к _ P_t (А в) Pt (В А ) .

вокруг константы

Модели первого рода также могут использоваться для переходов вида

А ^ В ^ С ^ —. С понижением количества А повышается количество В, которое понижается из-за перехода в С.

Реакции параллельного распада также могут быть смоделированы. Особенно интересными случаями являются случаи обратимых реакций (А ^ В и А ^ С) и реакций параллельного распада на рис. 10.

А ^ В

с

Рис. 10. Реакция параллельного распада. Реакции могут быть обратимыми

Химическая кинетика второго порядка

Несколько исследовательских групп разработали модели клеточных автоматов для конкретных реакционно-диффузионных систем [3]. В частности реакция Белоусова-Жаботинского была рассмотрена в нескольких исследованиях [4]. Также внимание было направлено на более простую реакцию А + В с С [1]. Рассматриваются и реакции вида А + В с С + D. В данных реакциях, как реагирующие вещества, так и продукты реакции свободно перемещаются по сетке за счет правил перемещения Р_т . Когда ингредиенты А и В встречаются в соседних ячейках сетки, то происходит их переход в С и D с вероятностью, которая задается в Р_Г(АВ ) . Симуляция такой модели происходит на торе, изначально ингредиенты случайно распределяются по сетке.

Правило концентрации второго порядка для реакции А + В с С: -[^ = ЦЛ][В] сохраняется в симуляциях           с           использованием           клеточных           автоматов.

В реакциях второго порядка, как и в реакциях первого порядка могут применяться обратимые правила (А + В ^ С + D ).

Вычислительный эксперимент

Для моделирования рассматриваются следующие реакции первого порядка:

• 1.    А с В вероятность р1.

• 2.    А с В с С вероятности р1, р2.

• 3.    А ^ В вероятности р1, р2.

• 4.   В <- А с С вероятности р1, р2.

• 5.  В « А с С вероятности р1, р2, р3.

Программные продукты для моделирования клеточных автоматов на языке Python : Python cellular-automaton [5], Python CellPyLib [6], Python netomaton [7], Python CellPyLib 3 D with animation [8]. Расширение CellPyLib , которое позволяет моделировать трехмерные клеточные автоматы.

В данной статье для проведения экспериментов используется CellPyLib . Его основные возможности:

• -    Позволяет моделировать простейшие одномерные и двумерные клеточные автоматы.

• -    Сетка клеточного автомата описывается матрицей или массивом, сохраняется состояние сетки на каждом из шагов моделирования.

• -    Позволяет визуализировать клеточные автоматы.

• -    Правила для клеточных автоматов задаются функцией, которая передается в функцию эволюции.

• -    Позволяет задавать окрестность Мура и фон Неймана произвольного радиуса.

• -    Основным недостатком данного программного продукта является то, что он не предоставляет возможность изменения состояний других клеток, находящихся в окрестности, так как из функции возвращается новое состояние только для текущей клетки, а не обновляется вся окрестность. Это не позволяет моделировать правила движения. Отсутствует возможность моделирования асинхронных автоматов с заданием разных последовательностей обновления клеток на сетке, что является необходимым для моделирования хим. реакций второго порядка.

Результаты моделирования реакций

Первая реакция

Уравнение концентрации для Л и В принимают следующий вид: ^] = к [Л] . Решением данного уравнения является экспоненциальная функция, для [Л] и [В] значение к имеет противоположные знаки, в силу увеличения концентрации количества В и снижения концентрации количества Л . На графике изменения концентрации Л и В для смоделированного клеточного автомата принимают экспоненциальный вид. На рис. 11 изображена визуализация реакции, а на рис. 12 изменение концентраций ингредиентов при моделировании реакции.

А -> В, Р(АВ) = 0.1, 50 X 50, 50 iterations

О 10       20       30       40

Рис. 11. Визуализация реакции 1

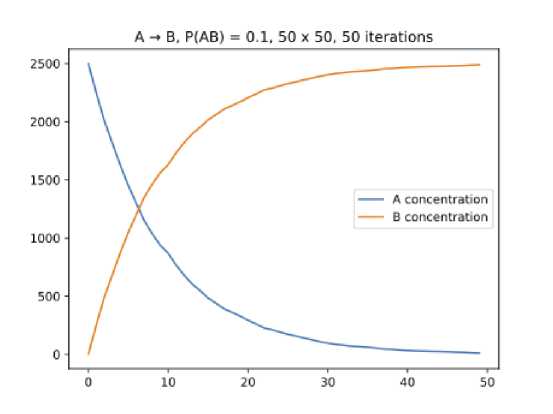
Рис. 12. График изменения концентраций ингредиентов в реакции 1

Вторая реакция

Реакции такого вида называются последовательными. На графике видно, что [ ] непрерывно снижается, значение [С] непрерывно повышается, а [В] достигает максимума и непрерывно снижается. На рис. 13 изображена визуализация реакции, а на рис. 14 изменение концентраций ингредиентов при моделировании реакции.

A - Б > С. Р(АВ) = 0.3, Р(ВС) = 0.2, 50 х 50, 50 iterations

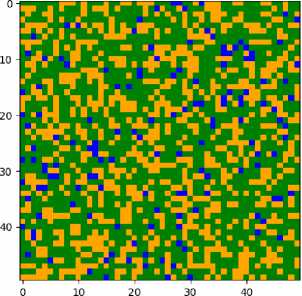
Рис. 13. Визуализация реакции 2

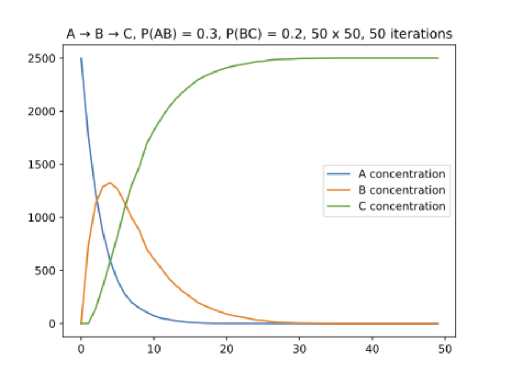
Рис. 14. График изменения концентраций ингредиентов в реакции 2

Третья реакция

Реакции такого рода называются обратимыми. В реакции такого вида А непрерывно переходит в В и В непрерывно переходит в А. Со временем значения концентраций становятся почти константа- ми, хотя маленькое количество ингредиентов продолжают непрерывно переходить друг в друга.

Равновесие концентраций определяется следующим образом: К =

[в] И

Pt (АВ )

. На графике можно Pt (ВА )

видеть, что на самых первых итерациях значения концентраций устанавливаются константами. Кон-

[В]     0.9

центрация ^

= 9. С увеличением объема ингредиентов флуктуации снижают свое зна-

чение, так как количества случайных реакций значительно ниже уже преобразовавшегося вещества. На рис. 15 изображена визуализация реакции, а на рис. 16 изменение концентраций ингредиентов при моделировании реакции.

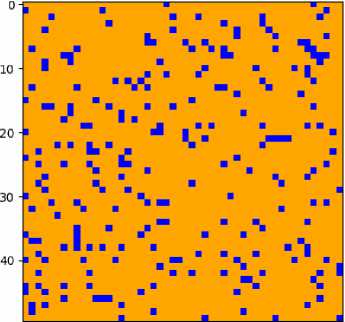
A « В, P(AB)=0.9, P(BA)=0.1, 50 x 50, 50 iterations

0        10       20       30       40

Рис. 15. Визуализация реакции 3

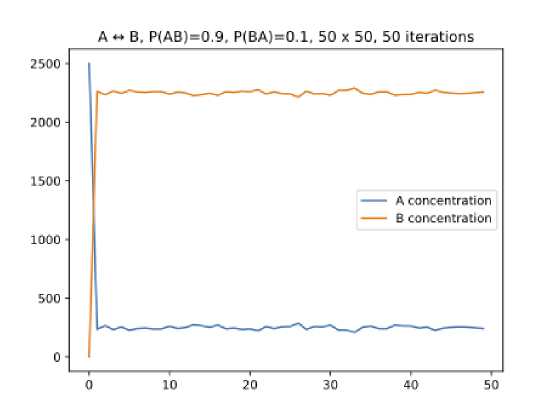
Рис. 16. График изменения концентраций ингредиентов в реакции 3

Четвертая реакция

Реакции такого вида называются параллельными, в них под-реакции "соревнуются" за то, чтобы произойти. Какая из реакций будет доминировать зависит от вероятностей переходов и как они соот- носятся друг с другом. На графике видно, что в данной реакции [Л] непрерывно падает, а значение

[В]     Р(АВ)    0.04

— = в(вс) = o~oi = 4. На рис 17 изображена визуализация реакции, а на рис. 18 изменение концен- траций ингредиентов при моделировании реакции.

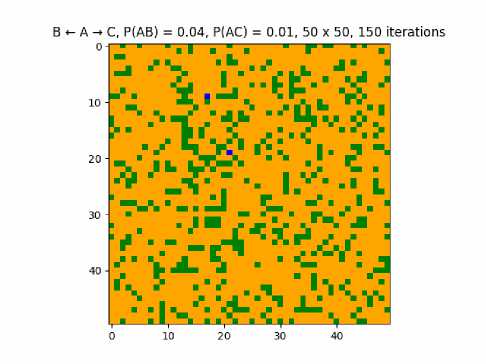
Рис. 17. Визуализация реакции 4

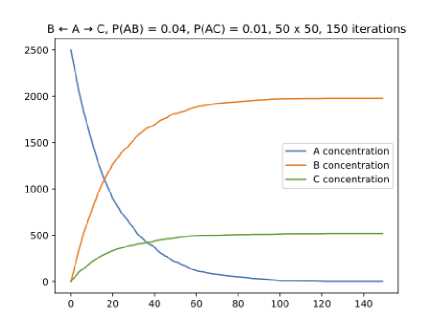
Рис. 18. График изменения концентраций ингредиентов в реакции 4

Пятая реакция

Для данной реакции уравнение концентрации принимает вид: ^] = /с3 [Л] « /с3/с (5Л)[5] , таким образом концентрация С сильно полагается на концентрацию S. На графике можно видеть, как концентрация С непрерывно увеличивается в силу того, что это конечное состояние в системе, а концентрации А и В непрерывно снижаются. При значительном превосходстве значений вероятности для реакции между А и В над переходом в С сначала достигается состояние пред-равновесия между А и В (если вероятности переходов между ними равны), но позже их концентрации непрерывно снижаются в силу появления все большего количества С. На рис. 19 изображена визуализация реакции, а на рис. 20 изменение концентраций ингредиентов при моделировании реакции.

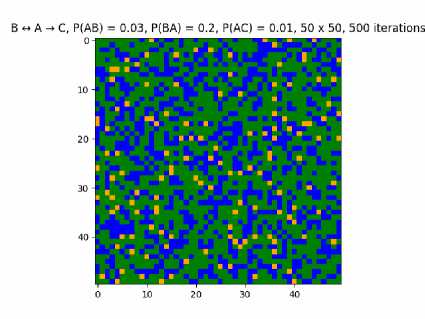
Рис. 19. Визуализация реакции 5

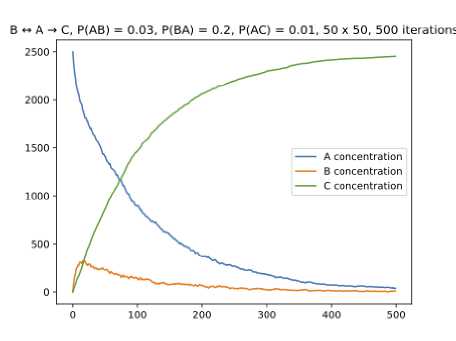
Рис. 20. График изменения концентраций ингредиентов в реакции 5

Заключение

В работе проведен анализ существующих методов моделирования химических реакций с использованием клеточных автоматов, выбраны химические реакции первого порядка для моделирования. Проведен анализ правил клеточных автоматов необходимых для программного моделирования выбранных химических реакций. С использованием языка Python и клеточных автоматов смоделированы химические реакции первого порядка. Визуализированы химические реакции первого порядка с отображением концентраций каждого из ингредиентов, участвующих в реакции. На основе данных, полученных на этапе моделирования, проведен анализ изменения концентрации ингредиентов, участвующих в реакции.