Моделирование и анализ распределения потенциала полевого эмиссионного катода на основе уравнений Лапласа и Пуассона
Автор: Чжоу Ф., Виноградова Е.М.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Физико-математические науки
Статья в выпуске: 12-3 (99), 2024 года.
Бесплатный доступ
В данной работе исследуется проблема распределения потенциала полевого эмиссионного катода с наконечной структурой, устанавливаются математические модели уравнений Лапласа и Пуассона, и модель решается методом разделения переменных. Результаты показывают влияние напряженности электрического поля и морфологии поверхности катода на распределение потенциала, что обеспечивает теоретическую основу для проектирования и оптимизации электронно-эмиссионной системы. Точность и достоверность модели проверены численным моделированием, что дает важные рекомендации по улучшению характеристик полевого эмиттера и оптимизации конструкции электрического поля.
Полевая электронная эмиссия, полевой эмиссионный катод, распределение потенциала, математическое моделирование, уравнение лапласа, уравнение пуассона, метод разделения переменных
Короткий адрес: https://sciup.org/170208580
IDR: 170208580 | DOI: 10.24412/2500-1000-2024-12-3-295-301
Текст научной статьи Моделирование и анализ распределения потенциала полевого эмиссионного катода на основе уравнений Лапласа и Пуассона
С непрерывным развитием современной науки и техники электронно-оптические системы находят все более широкое применение во многих областях, таких как высокоточные измерения, микро- и нанофабрикация и анализ поверхности. В этих приложениях технология электронной эмиссии играет решающую роль, особенно технология полевой электронной эмиссии в условиях высокой напряженности поля. Изучение физических механизмов и математическое моделирование не только углубляет понимание физических явлений, но и обеспечивает теоретическую поддержку для оптимизации конструкции соответствующих устройств.
Под полевой электронной эмиссией понимается явление потока электронов, испускаемого с поверхности проводника или жидкости под действием внешнего электрического поля высокой напряженности. Как один из основных компонентов электронно-оптической системы, форма и свойства материала катода для полевой эмиссии оказывают важное влияние на эффективность эмиссии и производительность системы. С помощью математического моделирования и численных расчетов
можно эффективно предсказать распределение потенциала и плотность тока в системе, чтобы обеспечить теоретическую основу для оптимизации конструкции.
Основной целью данного исследования является создание математической модели распределения потенциала для полевого эмиссионного катода с наконечной структурой и решение этой модели с использованием граничных условий. При этом используется метод разделения переменных, позволяющий преобразовать сложную краевую задачу в процесс решения в виде разложения по собственным функциям. Этот метод не только повышает эффективность решения задачи, но и может служить высокоточным ориентиром для последующего инженерного проектирования.
В данной работе представлена математическая модель, основанная на уравнениях Лапласа и Пуассона, процесс решения и его физическое значение, а также результаты численного моделирования и их прикладное значение.
-
2. Уравнение Лапласа
-
2.1. Математическая модель
-
) = 0 (1)
|
dU(x,y) _ dU(x,y) _ q dx X=X1 dx X=X2 dU(x,y) _ dU(x,y) _ q dx y=y1 dx y=y2 |
|
|
2.2. Решение |
AU = ~ + — =0 (4) dx2 dy2 U(x,y) = X(x)Y(y) * 0 (5) |
|
(4)(5)производное: |
Xy + xY = 0 (6) - = -=0 (7) X Y v 7 X = -a2 (8) Y = -P2 (9) a2 = —p2 (10) |
|
решить |
X + a 2 X = 0 (11) Y + p 2 Y = 0 (12) |
Характеристическое уравнение выводится следующим образом
X2 + α2 = 0(13)
X(x) = C1 cosαx + C2 sinα(14)
Y (y) = C3 cosβy + C4 sinβy(15)
U(x,y) = (C1 cosαx + C2 sinαx) · (C3 cosβy + C4 sinβy)(16)
потому что(1) - (2) = 0
X(x1) = 0 = C1 cosαx1 + C2 sinαx1
X(x1) = 0 = C1 cosαx2 + C2 sinαx2
Решено Лианли (17) (18)
cos ax1 + sin ax2 — cos ax2 sin ax1 = 0
ПП an =----
-
11 X 2 -X 1
Решено Лианли (10) (12)
zY ( y ) = с3еапУ — с4еапУ = shany = chany
Q — ПП pn = “ ~
y2-y1
X ( x ) = C 1 cos anx + C 1 sin anx = - sing x sin an(x — x 1 )
U (xy) = Z “=i sin a n (x - ^ 1 ) • (c 3 cos P y + C + sinpy]
потому что U ( x,y 1 ) = U ( x,y 2 ) = 0,Решено Лианли (20) (22)
Преобразование Фурье дает
U =V ” (a sh y ■ b shany-(y) )s i na (x — xy
UK^y) 2-in=1[ n shan(y2-(y1)) n shan(y2-(y1)y n 1
Uu = У “ (с^П^^^^
1(x, y) Zjn=1l n sh V n (y2-(y1)) n sh P n (y2- ( yiy)J n 1
c 12 ≤ min { c 1 , c 2 } ,
c 13 ≤ min { c 1 , c 3 } ,
c 23 ≤ min { c 2 , c 3 } , c 123 ≤ min { c 12 , c 23 , c 13} ,
где cK представляет собой стоимость коалиции для коалиции K. Эти параметры стоимости разработаны таким образом, чтобы затраты для любой коалиции не превышали ми-
3. Уравнение Пуассона математическая модель
нимальных затрат, с которыми сталкивается любой отдельный участник коалиции, тем самым снижая барьеры для формирования коалиции.
p(x, y) Av(x,y) = —±-^L £0
0 ≤ x ≤ a
0 ≤ y ≤ b
x0 - ε < x < x0 + ε x0 - ε < x < x0 + ε y0 - δ < y < y0 + δ
d2U d2U p(x,y)
dx2 + dy2 80
P(x,y){
X0 S 3.1. Решение ИтАрг2 Если е ^ 0,3 ^ О,^) $ Перенос из (12) дает Yn(y) = sin^y (29) U(x,y)=S“=i U^sin^y (30) В соответ ствии с граничными условиями для функции U получаем U"n(x)-^^un^=^v(x) I sin^ydy (31) 0 Jy-~8 (32) Для vn(x) э то будет иметь следующий вид U"n(x) -^U„M= 2g(cosn" 's) - cosn" ■ s)) (33) Получить U"n(x)-^^un{x) = ^ Я=1Ф1 Wsinl^ (34) Пусть vn(x ) заменяется на Un(x) = c1(x) ch^^x + c2(x)sh^x (35) Получить ci(x) = -^-sin^y (\i(X)sh^XdX + ci (36) 0 Z—ii=i 0 ci(x)= ^sin^V IX i(x)ch^xdx+ c2 (37) i=i 0 причина, о которой Un(x) = c^c^x+c^sb^x+^sm^ Y^sh^-x)^ (38) 0 i=i 0 Из vn(0) = vn(a) = 0 получаем с 2Sh2£a+JLy sin^sh^(a-x0yX°‘sb^-aU^O (39) пп£о / ii i xx--£ Следовательно ZN „ . . mi . ,пП, . ,пП X ’ 2T1 sm-^- yoi sh—(a—x0)sh—x 45 , nnVo X , nn , t----^^I^a----+ ^sm— ^ X pi(r^sh-(r—x)dr 1=1 1-1 Для x < x0 Un(x) = I N 1=1 „ mi пП, . пП 2ti sin-^-y0i sh—(a-x0)sh—x , пП nn£0sh—a Для x > x0 ZN mi ,пП, ,пПxX 2т1 sm-b Уо1 sh—(a-xo)sh—x 4Spj . nnv0 f ry ,nH , , ,. ----- ------“=77---------1--Sin---- (л (r) sh — (r — x) dr + _ nneoshmП■a nn£0 bJ0 rx= 45 • nTCVr\ I XXI пП X XI ^Sin—г I Pi(r')sh — (r—x')dr(42) Наконец, расширение потенциала имеет вид для x < x0 “"’■Д.,1 „ . . пи . , пП, , 2ti sin-Yy0i sh-(a-x0) n=1 nsh^a b sin—y. sh — x b 7 b Для x > x0 u""=Z_Z 2T1 sin-^-Уо1 sh—(xo) n=1 nsh^a b sin^y .shn.(a— x) 3.2. Картина эквипотенциалей Рис. 1. Poisson С помощью математического моделирования и решения проблемы распределения потенциала полевого эмиссионного катода с наконечной структурой в данной работе стоверность модели подтверждена численным моделированием, что обеспечивает теоретическую поддержку для оптимизации конструкции полевого эмиттера и улучшения эффективности эмиссии электронов. Будущие успешно построена теоретическая модель, основанная на уравнениях Лапласа и Пуассона, и решена задача распределения потенциала с использованием метода разделения переменных. Результаты показывают, что геометрия поверхности катода и напряженность элек- исследования могут расширить существующую модель, чтобы учесть более сложные физические эффекты, такие как изменение температуры и неоднородность материала, для более точного прогнозирования распределения потенциала и характеристик эмиссии в трического поля оказывают важное влияние на эффективность эмиссии электронов. До- практических приложениях.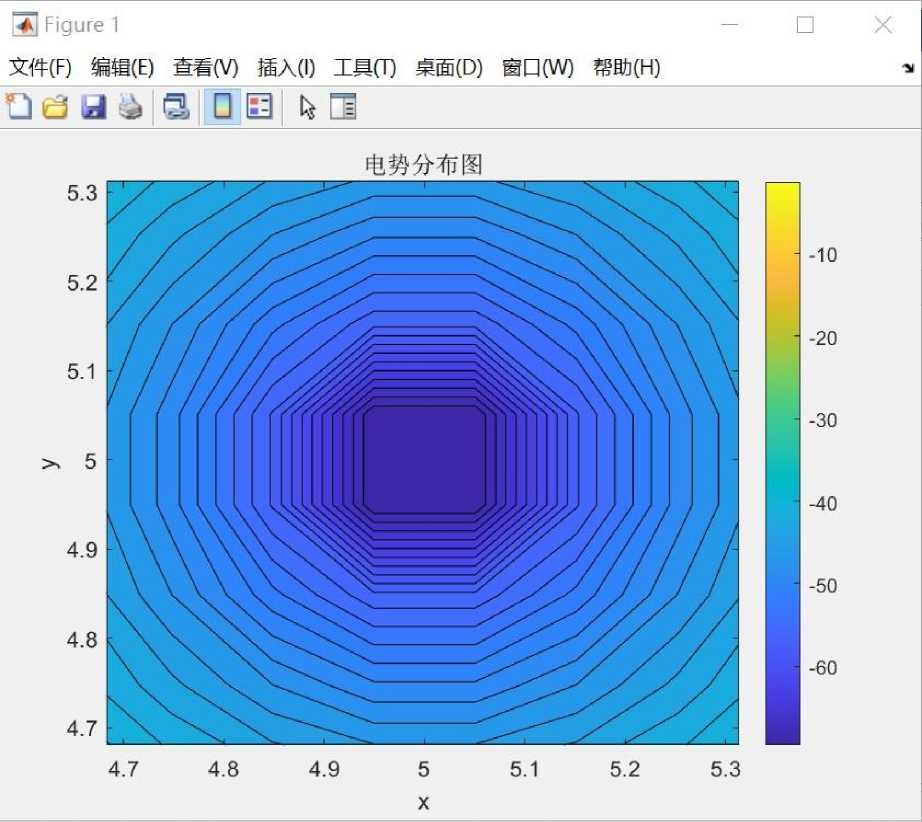
Заключение
Список литературы Моделирование и анализ распределения потенциала полевого эмиссионного катода на основе уравнений Лапласа и Пуассона
- Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1977.
- Миролюбов Н.Н., Костенко М.В., Левинштейн М.Л. Методы расчета электростатических полей. - М.: Высшая школа, 1963.
- Фурсей Г.Н. Автоэлектронная эмиссия // Соросовский образовательный журнал. - 2000. - Т. 6 (11). - С. 98-103.
- Виноградова Е.М. Математическое моделирование двумерной диодной системы с полевым эмиттером лезвийной формы / Е.М. Виноградова, Г.Г. Доронин, Н.В. Егоров // Журнал технической физики. - 2020. - Т. 90, № 4. - С. 540-543. DOI: 10.21883/JTF.2020.04.49075.140-19 EDN: EMQYDK
- Многослойные полевые эмиттеры, изготовленные из приведенных в контакт нанослоев гафния и платины / Г.Г. Соминский, В.Е. Сезонов, С.П. Тарадаев, С.Н. Вдовичев // Журнал технической физики. - 2019. - Т. 89, № 1. - С. 142-146. DOI: 10.21883/JTF.2019.01.46976.112-18 EDN: WCCVPY
- Многострийные кольцевые полевые эмиттеры с защитными металл-фуллереновыми покрытиями / Г.Г. Соминский, Т.А. Тумарева, Е.П. Тарадаев [и др.] // Журнал технической физики. - 2019. - Т. 89, № 2. - С. 302-305. DOI: 10.21883/JTF.2019.02.47086.124-18 EDN: ZGDJXV
- Фурсей Г. Полевая эмиссия в вакуумной микроэлектронике. - Шпрингер, 2005.
- Свонсон Л.В., Швинд Г.А. Рассеяние электронов, испускаемых полем. - Handbook of Charged Particle Optics, 2009.
- Модинос A. Полевая, термоионная и вторично-электронная эмиссионная спектроскопия. - Plenum Press, 1984.


