Моделирование и идентификация процесса охлаждения и затвердевания непрерывнолитых слябовых заготовок
Автор: Панферов В.И., Панферов С.В.
Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy
Рубрика: Металлургическая теплотехника и теплоэнергетика
Статья в выпуске: 1 т.24, 2024 года.
Бесплатный доступ
Введение. Рассматривается задача параметрической идентификации математической модели процесса охлаждения и затвердевания непрерывнолитых слябов в зоне вторичного охлаждения (ЗВО) машин непрерывного литья заготовок (МНЛЗ). Актуальность работы обуславливается прежде всего тем, что качество получаемого таким образом изделия в существенной мере зависит от режима работы ЗВО. Технологический процесс достаточно сложный, не полностью изученный и, как следствие, пока еще плохо управляемый. Цель исследования: разработать процедуру параметрической идентификации модели процесса охлаждения и затвердевания металла по данным доступных для непосредственного измерения величин.
Машина непрерывного литья заготовок, зона вторичного охлаждения, математическое моделирование, параметрическая идентификация модели, коэффициент теплоотдачи, метод наименьших модулей
Короткий адрес: https://sciup.org/147243231
IDR: 147243231 | УДК: 669.046:621.746.6.001.57 | DOI: 10.14529/met240108
Текст научной статьи Моделирование и идентификация процесса охлаждения и затвердевания непрерывнолитых слябовых заготовок
Постановка задачи
Качество слитков, получаемых на МНЛЗ, в значительной мере определяется рациональной организацией теплоотвода в зоне вторичного охлаждения (ЗВО). На практике режимы охлаждения заготовок обычно подбирают экспериментальным путем – посредством анализа качества литого металла для различных расходов охладителя по секциям ЗВО. Однако такой способ решения задачи является весьма трудоемким, поэтому представляется целесообразным применение математического моделирования для исследования и оптимизации режимов охлаждения заготовок.
Известно [1–7], что процесс охлаждения и затвердевания металла в ЗВО слябовых МНЛЗ удовлетворительно может быть описан с помощью математической модели следующей структуры:
сР?_7-(л?),0<х<1,т>0;(1)
r дт дх\ дх/
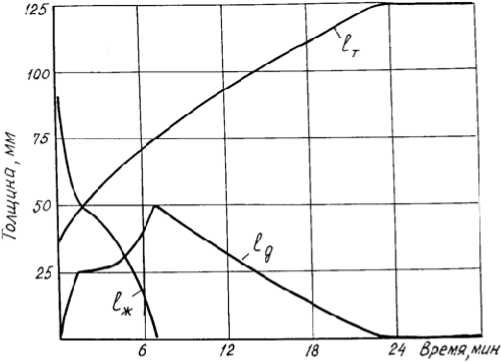
t(x, 0) = t0(x), 0 д^=0,т>0;(3) дх ^dt(l,T) _ {ГСс(т)+27314 _ Гс(;,т)+27314} + дх _ 0Ч. 100 J L 100 J } +a[tc(r) - t(l, t)], t > 0,(4) где с, р, Л - соответственно эффективная теплоемкость, плотность и коэффициент тепло- проводности, зависящие от температуры в данной точке х в данный момент времени т -t(x,T); t0(x) - заданная функция, описывающая температурное поле в заготовке после выхода из кристаллизатора; tc(T) - температура окружающей среды; и и а - параметры внешнего теплообмена; I - расчетное сечение слитка. В модели (1)–(4) используются известные [1–7] представления о двухфазной зоне слитка, согласно которым учет выделения теплоты кристаллизации сводится к соответствующему заданию зависимости эффективной теплоемкости от температуры. Данная величина рассчитывается по трехинтервальной формуле – соответственно для твердого и жидкого металла и двухфазной зоны заготовки. Границы двухфазной зоны слитка, отделяющей твердый металл от жидкой фазы, определяются по температурному полю заготовки – на границах должны достигаться температуры ликвидуса и солидуса соответственно. Расчет процесса охлаждения и затвердевания заготовок по модели (1)–(4) обеспечивает достаточную для практических целей точность, если удовлетворительно определены реальные значения параметров внешнего теплообмена и и а, т. е. решена задача параметрической идентификации [8–12]. Множество факторов технологического и конструктивного характера, влияющих на теплообмен в зоне, не позволяет параметры и и а вычислять только расчетным способом [5, 8–12]. Решение задачи параметрической идентификации Исходной информацией для идентификации математической модели являются уравнения (1)–(4) и результаты наблюдения за поведением входов и выходов объекта [13, 14]. В данном случае входом объекта является температура окружающей среды, в качестве выхода используются значения температуры поверхности сляба в разных точках технологической линии. Подчеркнем, что все эти величины определяются непосредственным измерением на объекте. Задачу идентификации сформулируем следующим образом: требуется определить такие значения параметров внешнего теплообмена, при которых критерий l=SMt 4Uy)-tP(Uy)|, (5) где tэ(/, ту), tр(/, ту) - соответственно экспериментальное и расчетное значения темпера- туры поверхности заготовки; ту - используемые в эксперименте моменты времени; п -число экспериментальных точек, принимает наименьшее из возможных значение. Как это следует из формулы (5), для настройки модели на «реальный процесс» применен метод наименьших модулей, характеризующийся значительно меньшей чувствительностью к выбросам экспериментальных данных по сравнению с методом наименьших квадратов. Задача параметрической идентификации модели (1)–(4) решалась с учетом следующих обстоятельств. Параметры внешнего теплообмена и и а имеют различные значения для разных секций ЗВО и определяются в основном расходом охладителя. При решении же задачи идентификации (параметрической настройки модели) возможны такие наборы экспериментальных данных, когда на каждую секцию ЗВО приходится хотя бы две точки измерения температуры поверхности и когда таких точек измерения нет. Предельный случай последней ситуации – когда измеряется температура поверхности металла только в пределах последней секции ЗВО. В случае наличия хотя бы двух точек измерения температуры поверхности сляба в границах каждой секции ЗВО решение задачи можно упростить, решая задачу самостоятельно для каждой секции и последовательно, переходя по секциям от начала к концу технологической линии, аналогично тому, как это делалось в работе [11]. Однако при таком подходе может получиться так, что будут определены только близкие к оптимальным значения параметров теплообмена, а не их оптимальные значения. Дело в том, что если на величину локальных разностей расчетной и экспериментальной температур поверхности заготовки для первой секции влияют значения параметров теплообмена только этой секции, то для последующих секций величина локальных разностей температур будет зависеть не только от выбора значений параметров теплообмена для этой секции, но и всех предыдущих секций. В последнем случае решение задачи идентификации существенно усложняется: задачу нужно решать сразу для всей ЗВО, при этом число отыскиваемых параметров может быть достаточно большим. Решение задачи первым методом будет полностью оправдано, если только удастся найти такие значения параметров теплообме- на, при которых локальные разности температур для каждой секции будут практически равны нулю. В этом случае мы действительно будем находиться в точке глобального минимума критерия идентификации. Отметим, что опыт решения таких задач [11] показал, что данное условие, как правило, выполняется, поэтому решение задачи идентификации для всей ЗВО в целом заменяли решением отдельных, более простых задач идентификации для каждого участка постоянства параметров внешнего теплообмена, таковым считалась отдельная секция ЗВО. Конечно, при этом соответствующим образом организовали и экспериментальные замеры температур: если модель внешнего теплообмена задана в лучисто-конвективной форме, то в границах каждой секции температура поверхности должна быть измерена не менее чем в двух точках [15]. Получающееся существенное упрощение частных задач обусловлено меньшей размерностью вектора искомых параметров внешнего теплообмена. При этом частные задачи решали последовательно по участкам, перемещаясь от начала к концу ЗВО. Для случая лучисто-конвективной модели внешнего теплообмена задачу идентификации решали с помощью программы, реализующей метод покоординатного спуска, получающиеся при этом задачи одномерной минимизации решали с помощью подпрограммы, использующей метод золотого сечения. Причем для численного интегрирования уравнений (1)–(4) применяли неявную конечно-разностную схему, которую решали методом прогонки [16, 17]. Изменение численных значений с, р, Л в зависимости от температуры для твердого металла рассчитывали по аппроксимирующим уравнениям работы [18], в других случаях использовали данные работ [19, 20]. Эффективную теплоемкость двухфазной зоны оценивали по способу Ю.А. Самойловича [1, 2], при этом теплоту затвердевания сталей задавали согласно данным [19]. Причем с целью упрощения вычислений при расчете температурного поля на текущем временном интервале значения с, р,Л определяли по температурам на предыдущем временном слое. Погрешность вычислений от этого, как это хорошо известно, будет незначительной. Температуры ликвидуса и солидуса, указывающие границы двухфазной зоны слитка, вычисляли по эмпирическим уравнениям работы [20]. Результаты исследования В расчетах температурное поле заготовки после выхода из кристаллизатора сначала, следуя известным литературным рекомендациям, описывали уравнением t0(x) = tn + (£ж -£пИ1-|), (6) где £п - температура поверхности слитка после выхода из кристаллизатора; £ж - температура жидкого металла в кристаллизаторе. Однако, как показал опыт моделирования, данное уравнение не приемлемо для описания начального температурного поля сляба в зоне вторичного охлаждения, в этом случае толщина твердой корочки металла получается существенно завышенной. В самом деле, пусть £п = 1200 °С, £ж = 1500 °С, а температура ликвидуса равна 1500 °С, тогда границу х жидкой фазы следует отыскивать из неравенства 1200+ (1550- 1200) 41-^) > 1500. (7) Решая это неравенство, получим х<^, (8) что не соответствует практическим данным. Далее начальное температурное поле заготовки пытались описывать квадратичным полиномом вида t0(x) = а + Ьх + сх2. (9) При этом толщину затвердевшего металла вычисляли по соотношению к • ^т^р [3], где к - коэффициент затвердевания, а ткр -время прохождения металлом кристаллизатора: ткр = /кр/тр. Здесь /кр - высота кристаллизатора, тр - скорость разливки, также при этом считалось, что температура затвердевшего металла на границе с двухфазной зоной равна температуре солидуса. Однако в этом случае вершина параболы располагается в промежуточной точке между центром и поверхностью заготовки (якобы промежуточные точки имеют более высокую температуру, чем центр), что тоже противоречит фактическим данным. Следовательно, и такой подход не приемлем для описания начального температурного поля сляба. Установили, что реальное начальное температурное поле заготовки удовлетворительно описывается с помощью следующего соотношения: t0(%)4 ( a + b • (% t , если % ж кр - k ■ ^т^ ), если l> % > k • ^тКр, здесь параметры a и b вычисляются из условия, что на поверхности заготовки наблюдается температура tп, а температура твердого металла на границе с двухфазной зоной равна температуре солидуса. В результате большого количества расчетов было установлено, что рассматриваемая задача идентификации решается устойчиво и практически с любой наперед заданной точностью. При этом увеличение числа точек измерения существенно повышает помехоустойчивость решения. Если внешний теплообмен описать только в конвективной форме, используя понятие так называемого суммарного коэффициента теплоотдачи [1, 2], то в этом случае критерий идентификации (5) будет зависеть только от одного параметра – упомянутого суммарного коэффициента теплоотдачи. Для отыскания оптимального значения этого коэффициента можно ис- пользовать любой одномерный метод минимизации, причем для реализации изложенного способа идентификации в пределах каждой расчетной зоны достаточно иметь только одну экспериментальную точку [15]. Нами для этого случая разработана и апробирована программа, использующая метод золотого сечения. Распространенным методом определения суммарного коэффициента теплоотдачи является способ, основанный на тепловом расчете количества испарившейся воды. Однако процедура определения численного значения коэффициента испарения является весьма приближенной, вследствие этого точность отыскания параметра теплообмена данным способом не может быть высокой. Рассмотренный метод позволяет значительно точнее решать данную задачу. На рис. 1 представлены рассчитанные по настроенной модели кривые изменения во Рис. 1. Графики изменения температуры поверхности и центра заготовки Fig. 1. Graphs of changes in temperature of the surface and center of the workpiece Рис. 2. Кривые изменения толщины жидкой, двухфазной и твердой фаз заготовки Fig. 2. Curves of changes in the thickness of the liquid, two-phase and solid phases of the workpiece времени температур центра t(0, т) и поверхности заготовки t(l, т), а на рис. 2 - толщины жидкой 1ж, двухфазной 1д и твердой фаз 1т сляба из стали марки 17ГС для зоны вторичного охлаждения MНЛЗ кислородно-конвертерного цеха (ККЦ) ПАО «ММК». Здесь ур = 0,5 м/мин; 1кр = 1,1 м; tж = 1531 °С; tn = 1204 °С; l = 0,125 м. Как это нетрудно заметить, характер изменения кривых вполне соответствует практическим данным. Найденные в процессе идентификации численные значения суммарного коэффициента теплоотдачи соответственно для секций 1–7-й зон вторичного охлаждения составили: 520,2; 618,6; 281,2; 203,7; 181,0; 170,8; 138,2 Вт/(м2 • К). Большее значение коэффициента внешнего теплообмена для второй секции, чем для первой, объясняется большим расходом охладителя на данную секцию. Выводы Разработанная математическая модель позволила изучить существующие режимы охлаждения металла в зоне вторичного охлаждения МНЛЗ ККЦ ПАО «ММК», в частности, установлена необходимость определенной корректировки расходов охладителя вдоль технологической линии.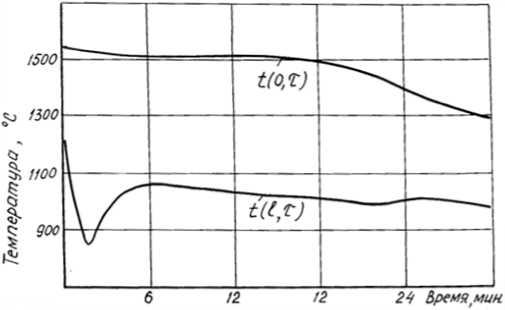
Список литературы Моделирование и идентификация процесса охлаждения и затвердевания непрерывнолитых слябовых заготовок
- Тепловые процессы при непрерывном литье стали / Ю.А. Самойлович, С.А. Крулевицкий, В.А. Горяинов, З.К. Кабаков. М.: Металлургия, 1982. 152 с.
- Лисиенко В.Г., Самойлович Ю.А. Теплотехнические основы технологии и конструирования машин непрерывного литья заготовок. Красноярск: Изд-во Краснояр. ун-та, 1986. 121 с.
- Цаплин А.И., Никулин И.Л. Моделирование теплофизических процессов и объектов в металлургии: учеб. пособие. Пермь: Изд-во ПГТУ, 2011. 299 с.
- Лукин С.В. Теплотехническое обоснование методов контроля и управления режимами охлаждения слитка на МНЛЗ: автореф. дис. … канд. техн. наук. Череповец: Череповецкий гос. ун-т, 1998. 24 с.
- Вдовин К.Н., Панферов В.И., Горосткин С.В. Идентификация математической модели процесса охлаждения и затвердевания непрерывнолитых слябовых заготовок // Известия вузов. Черная металлургия. 1998. № 8. С. 58–60.
- Бирюков А.Б., Иванова А.А. Современные подходы к эффективному управлению теплотехническими процессами в зоне вторичного охлаждения МНЛЗ // Черная металлургия. Бюллетень научно-технической и экономической информации. 2015. № 3. С. 46–52.
- Бирюков А.Б., Иванова А.А. Современные подходы к математическому моделированию теплотехнических процессов в литейно-прокатных модулях на участке МНЛЗ – Нагревательное устройство // Бюл. НТИ «Черная металлургия». 2015. № 7. С. 50–55.
- Ткаченко В.Н., Иванова А.А., Василян Г.Р. Идентификация параметров внешнего теплообмена в зоне вторичного охлаждения МНЛЗ // Вестник Национального технического университета «Харковский политехнический институт». Тематический выпуск: Информатика и моделирование. 2007. № 39. С. 168–177.
- Ткаченко В.Н., Иванова А.А., Шуба О.В. Методы и алгоритмы идентификации параметров внешнего теплообмена процессов тепломассопереноса // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2008. Т. 8. Вып. 1. С. 58–64.
- Панферов В.И. Об одном решении задачи идентификации параметров моделей внешнего теплообмена металла в нагревательных печах // Известия вузов. Черная металлургия. 1988. № 1. С. 135–139.
- Панферов, В.И. Идентификация математической модели нагрева металла в печах // Известия вузов. Черная металлургия. 1990. № 9. С. 86–89.
- Бирюков А.Б. Совершенствование теплотехнических параметров систем производства непрерывнолитой заготовки и ее тепловой обработки. Донецк: Ноулидж (Донецкое отделение), 2013. 472 с.
- Растригин Л.А., Маджаров Н.Е. Введение в идентификацию объектов управления. М.: Энергия, 1977. 216 с.
- Растригин Л.А. Современные принципы управления сложными объектами. М.: Советское радио, 1980. 232 с.
- Вдовин К.Н., Горосткин С.В., Панферов В.И. Совершенствование работы зоны вторичного охлаждения машины непрерывного литья заготовок // Известия вузов. Черная металлургия. 1998. № 4. С. 50–54.
- Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло- и массообмена. М.: Наука, 1984. 286 с.
- Никитенко Н.И. Исследование нестационарных процессов тепло- и массообмена методом сеток. Киев: Наукова думка, 1971. 267 с.
- Маковский В.А., Лаврентик И.И. Алгоритмы управления нагревательными печами. М.: Металлургия, 1977. 183 с.
- Журавлев В.А., Китаев Е.М. Теплофизика формирования непрерывного слитка. М.: Металлургия, 1974. 216 с.
- Нисковских В.М., Карлинский С.Е., Беренов А.Д. Машины непрерывного литья слябовых заготовок. М.: Металлургия, 1991. 272 с.


