Моделирование и экспериментальное исследование упрочнения цилиндрических изделий методом совместного упругопластического деформирования растяжением и кручением

Для изделий, работающих в условиях периодически меняющихся нагрузок, крайне важными являются характеристики надёжности и долговечности. С целью повышения данных характеристик, прежде всего предела выносливости, применяют разнообразные методы упрочнения. Один из таких методов заключается в наведении в приповерхностной области длинномерного цилиндрического изделия благоприятных сжимающих остаточных напряжений за счет последовательного пластического деформирования сначала растяжением, а затем, при фиксации полученной при растяжении продольной деформации, кручением [1-5]. Данный способ упрочнения обладает рядом преимуществ, важнейшими из которых являются следующие:

– на стадии растяжения восстанавливается пространственная геометрия длинномерного цилиндрического изделия;

– достигается достаточно большая глубина залегания остаточных сжимающих напряжений, наведённых в процессе упрочнения (около 1/3 радиуса от поверхности), что является важным фактором при работе изделия в коррозионной среде;

– устраняются пики остаточных напряжений, достигается достаточно равномерное распределение напряжений по длине изделия.

Существующие режимы упрочнения включают стадии растяжения, возможной частичной разгрузки после растяжения, фиксации достигнутой линейной деформации ε на постоянном уровне и последующего однократного кручения.

Цель настоящего исследования: изучение и обоснование преимуществ применения принципиально новых режимов упрочнения, при которых после стадии растяжения и фиксации достигнутой линейной деформации осуществляется кручение со сменами направления закручивания (знакопеременное кручение).

На первом этапе изучались качественные зависимости между напряжениями и деформациями при напряженном состоянии, характерном для процесса упрочнения. Для этого построена математическая модель совместного упругопластического деформирования растяжением и кручением тонкостенного трубчатого образца, основные положения которой рассмотрены в [6]. Определяющие уравнения модели, основанной на классической теории течения, включают ряд функций. Параметры данных функций, а также такие механические характеристики материала, как условный предел текучести σ 02 , модули Юнга E и сдвига G – являются входными параметрами модели. С целью определения данных входных параметров и подтверждения основных положений модели были проведены исследования в Центре экспериментальной механики ПНИПУ (ПГТУ) на универсальной двухосевой сервогид-равлической испытательной системе Instron

8850. Эксперименты выполнялись на тонкостенных трубчатых образцах с наружным диаметром 12 мм и толщиной стенки 1 мм, у которых напряженное состояние в их рабочей части можно считать практически однородным. Исследовались стали, применяемые для изготовления нефтенасосных штанг. Подробно результаты испытаний на растяжение, чистый сдвиг и совместное растяжение и кручение рассмотрены в [7, 8].

Параметрами модели деформирования тонкостенного трубчатого образца на выходе являются величины напряжений и деформаций, а именно: нормальное напряжение ст ; касательное напряжение т , полная линейная деформация г , а также её составляющие - упругая e e и пластическая e p ; полная угловая деформация у , а также её составляющие - упругая y e и пластическая y p . Модель показывает достаточно точное соответствие результатам экспериментов на стадиях, представляющих интерес для упрочнения изделия. На основе полученной модели деформирования тонкостенного трубчатого образца построена математическая модель упрочнения совместным упругопластическим деформированием растяжением и кручением стержня сплошного круглого сечения. Данная модель позволяет оценить распределение по поперечному сечению изделия остаточных нормальных и касательных напряжений, наведённых в процессе упрочнения.

Основные положения принятой модели:

• 1.    Стержень сплошного круглого сечения разбивается на n тонкостенных цилиндров со средним радиусом R i и толщиной стенки δ i , где δ i <<  R i . Деформирование каждого такого цилиндра в отдельности описывается моделью тонкостенного трубчатого образца, рассмотренной в [6].

• 2.    Принимаются гипотезы плоских сечений и прямых радиусов. Вследствие этого все тонкостенные цилиндры получают одинаковые общие продольные деформации, а угловые деформации связаны между собой линейной зависимостью:

• 3.    Величины продольных сил ( N ) и крутящих моментов ( M ) в процессе нагружения определяются соотношениями:

R

£ i = const ,       Y =       • Y max ,

^R max             (1)

где γ max – угловая деформация наружного цилиндра, R max – средний радиус наружного цилиндра.

N = 2 ( 2 • n • R,- 5_r c i )

i

M = 2 ( 2 • n • ( R i ) 2 • 5 i • T i )

i                                            (2)

остаются остаточные деформации и остаточные напряжения. В соответствии с теоремой о разгрузке [9] величины остаточных деформаций ( ε os , γ os ) определяются как разности между деформациями, возникающими при нагружении, и уменьшениями деформаций при разгрузке и в конечном итоге приводятся к следующим выражениям:

2 ( R i- bf £ pi )         2 ( R i- 5г Y pi )

• ^£ os =                 , ^Y os =

• 5.    По найденным значениям остаточных деформаций вычисляются значения остаточных напряжений:

2(Ri-5,)         Л R2_1

i                   2-^ 5

i V Rm ax   )(3)

• ^c osi = E • ( £ os ^{- £} pi )

^Ri       1

• ^T osi    G I Y os q       Y pi I ,

• V     R m ax      )                 (4)

где σ osi и τ osi – остаточные нормальные и касательные напряжения в i -том цилиндре.

Пошаговый процесс определения всех параметров, в т.ч. включающий конечноразностное решение уравнений модели тонкостенного трубчатого образца, реализован на компьютере. Параметрами на выходе модели упрочнения стержня круглого сечения являются: продольная сила N , кН; крутящий момент , ,                                                                _Y max ^{1 1}

M , Н-м; угол закручивания ф, рад И = r I , где l V         '’max )

– длина рабочей части изделия); остаточные нормальные напряжения ст _os , МПа; остаточные касательные напряжения т _os , МПа. Для проверки адекватности модели проведены испытания на образцах круглого сечения с диаметром рабочей части 10 мм и длиной рабочей части 40 мм. Эксперименты выполнялись на универсальной двухосевой сервогидравлической испытательной системе Instron 8850. На рис. 1 представлено сравнение теоретических и экспериментальных зависимостей при одном из исследуемых режимов упрочнения. На рис. 2 представлено распределение согласно модели остаточных напряжений по радиусу поперечного сечения образца, наведённых при данном режиме упрочнения. При этом входными параметрами модели, за исключением размеров рабочей части изделия, являются те же, что и для модели деформирования тонкостенного образца, определённые ранее для исследуемых сталей в результате экспериментов. Достаточно точное соответствие теоретических и экспериментальных зависимостей на рис. 1, в том числе и на частично оставленной третьей стадии кручения, подтверждает адекватность модели.

Испытания при других значениях предварительного нормального напряжения растяжения и амплитуды стадий кручения также подтверждают адекватность модели на стадиях растяжения, возможной частичной разгрузки после растяжения и последующих двух полных и третьей частичной стадиях кручения.

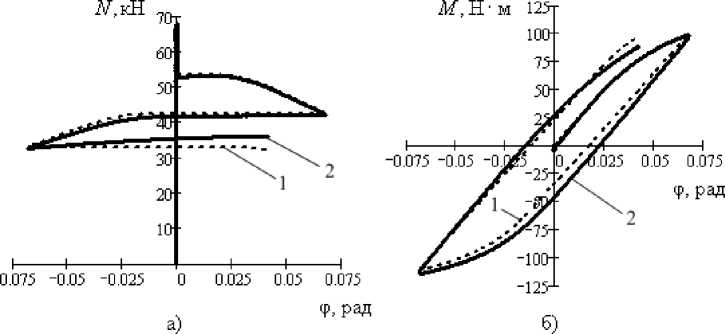
Рис. 1. Графики зависимостей: а) продольной силы, б) крутящего момента от угла закручивания при упрочнении образца круглого сечения из стали 15Х2ГМФ в последовательности: растяжение до σ 02 , разгрузка до σ = 0,8·σ 02 , фиксация достигнутой деформации ε на постоянном уровне, кручение образца до φ = φ а (φ а = 0,068 рад), кручение в противоположную сторону до φ = – φ a , кручение в первоначальном направлении до φ = 0,042 рад. 1 – теоретические графики, 2 – экспериментальные графики

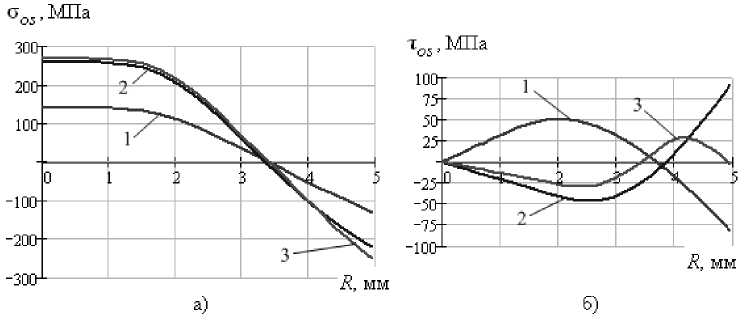
Рис. 2. Распределение остаточных нормальных (а) и остаточных касательных (б) напряжений по радиусу поперечного сечения образца из стали 15Х2ГМФ после: 1 – первой, 2 – второй и 3 – третьей стадии кручения при упрочнении в последовательности: растяжение до σ 02 , разгрузка до σ = 0,8·σ 02 , фиксация достигнутой деформации ε на постоянном уровне, кручение образца до φ = φ а (φ а = 0,068 рад), кручение в противоположную сторону до φ = – φ a , кручение в первоначальном направлении до φ = 0,042 рад.

На рис. 2а можно видеть, что после каждой из стадий кручения постепенно увеличивается по абсолютному значению величина остаточных сжимающих напряжений в приповерхностной области, но в то же время возрастает и величина остаточных растягивающих напряжений в середине сечения. Глубина залегания остаточных сжимающих напряжений составляет около 1/3 радиуса от поверхности. Частичная третья стадия кручения оставлена специально для минимизации величины остаточных касательных напряжений, наведённых в процессе упрочнения. Это можно видеть на рисунке 2б, где после третьей стадии кручения их величина вдоль радиуса много меньше, чем после первой и второй стадий.

Среди критериев наиболее благоприятного распределения остаточных напряжений по поперечному сечению изделия можно выделить следующие:

– в приповерхностной области наводятся наибольшие по абсолютному значению остаточные сжимающие напряжения, положительно влияющие на повышение предела выносливости изделия;

– в сердцевине стержня наводятся наименьшие остаточные растягивающие напряжения, отрицательно сказывающиеся при наложении на рабочие напряжения в изделии (например, на рас- тягивающее напряжение в штанге), желательно, чтобы сердцевина оставалась упругой;

– по всей области поперечного сечения наводятся минимальные остаточные касательные напряжения, которые также могут отрицательно сказаться при наложении на напряжения, возникающие при работе изделия;

– возникает достаточно большая глубина залегания остаточных сжимающих напряжений, которая превосходит глубину проникновения коррозионных язв при работе изделия в агрессивной среде.

Исходя из данных критериев, могут быть определены наиболее благоприятные режимы упрочнения. На рис. 3 представлено распределение остаточных напряжений по радиусу поперечного сечения после упрочнения по одному из наиболее оптимальных режимов в сочетании растяжения и однократного кручения. На рис. 4 представлено распределение остаточных напряжений после упрочнения по одному из предлагаемых новых режимов в сочетании растяжения и знако- переменного кручения. И в случае режимов упрочнения с однократным кручением, и в случае режимов со знакопеременным кручением достигается достаточная глубина залегания остаточных сжимающих напряжений. Однако, обеспечивая и в том и в другом случае выполнение условия прочности в сердцевине, при упрочнении в сочетании растяжения и знакопеременного кручения на поверхности удаётся навести большие по абсолютному значению остаточные сжимающие напряжения. При этом благодаря частичной третьей стадии кручения минимизируется величина остаточных касательных напряжений. На рис. 4б касательные напряжения вдоль радиуса не превышают величины 25 МПа, что на один порядок меньше величины остаточных сжимающих напряжений, наведённых в приповерхностной области. В случае же режимов упрочнения с однократным кручением в приповерхностной области наводятся и остаточные нормальные, и остаточные касательные напряжения одного порядка, что видно на рисунке 3а, б.

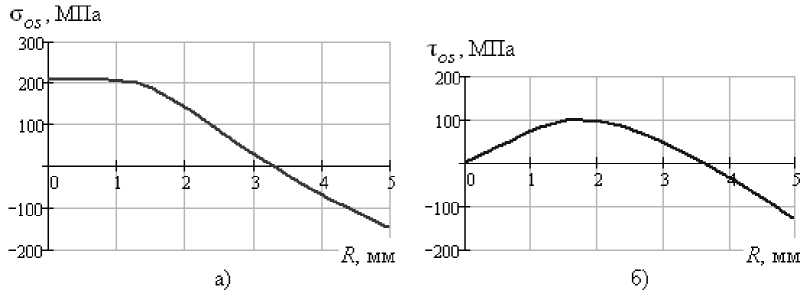
Рис. 3. Распределение остаточных нормальных (а) и остаточных касательных (б) напряжений по радиусу поперечного сечения образца при его упрочнении в последовательности: растяжение до σ 02 , разгрузка до σ = 0,75·σ 02 , фиксация достигнутой деформации ε на постоянном уровне, кручение образца до φ = 0,096 рад.

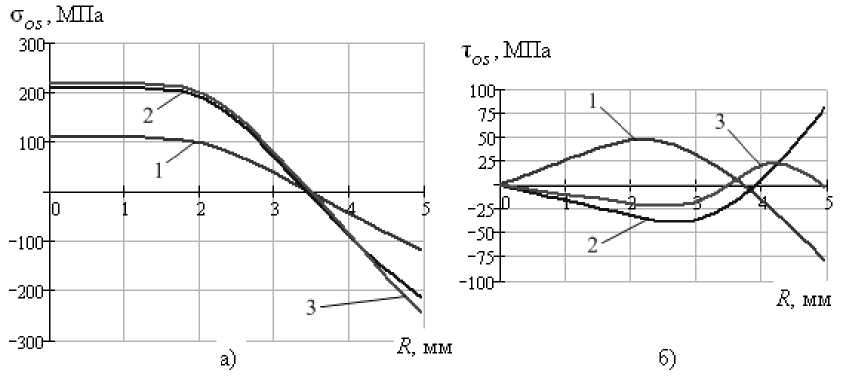
Рис. 4. Распределение остаточных нормальных (а) и остаточных касательных (б) напряжений по радиусу поперечного сечения образца после: 1 – первой, 2 – второй и 3 – третьей стадии кручения при упрочнении в последовательности: растяжение до σ 02 , разгрузка до σ = 0,75·σ 02 , фиксация достигнутой деформации ε на постоянном уровне, кручение образца до φ = φ а (φ а = 0,064 рад), кручение в противоположную сторону до φ = – φ a , кручение в первоначальном направлении до φ = 0,043 рад.

Выводы: упрочнение длинномерных цилиндрических изделий методом упругопластического деформирования, включающим стадии растяжения, фиксации достигнутой при растяжении продольной деформации на постоянном уровне и последующего кручения со сменами направления закручивания обладает рядом преимуществ. Для подтверждения практической значимости данных преимуществ предполагается провести усталостные испытания в коррозионной среде нескольких партий образцов из одной стали: партию базовых не упрочнённых образцов, упрочнённых по режиму с однократным кручением и упрочнённых по режиму со знакопеременным кручением. По результатам испытаний выявить действительную эффективность предлагаемых новых режимов упрочнения.