Моделирование и оптимизация динамической нагруженности силовых передач машинно-тракторных агрегатов

Динамическая нагруженность силовых передач машинно-тракторных агрегатов определяется их динамическими свойствами и характеристиками, динамикой агрегатируемых орудий, взаимодействием их с объектом труда и воздействием окружающей среды на агрегат. При создании новых агрегатов влияние навесного или прицепного оборудования на динамику силовой передачи базовой машины рассматривается в недостаточном объеме, в результате снижаются показатели надежности машин.

Экспериментальные исследования для выбора рациональных проектных параметров машинных агрегатов и оценки динамических свойств силовой передачи базового трактора приводят к значительным затратам.

В связи с этим, создание расчетных методов моделирования, оценки характеристик нагруженности и совершенствования динамических свойств силовых передач при конструировании специальных машинных агрегатов на базе серийных тракторов, является актуальной научно-технической проблемой.

Цель работы. Разработка методов математического моделирования, оценки характеристик нагру-женности и совершенствования динамических свойств на основе структурной оптимизации силовых передач машинно-тракторных агрегатов с активными и пассивными рабочими органами.

Рассмотрены следующие задачи исследования:

построение математических моделей и нахождение динамических характеристик силовой передачи машинно-тракторного агрегата с активными и пассивными рабочими органами, как системы с большим числом степеней свободы;

оценка динамических характеристик экспериментальных нестационарных тензометрических процессов нагруженности силовых передач на основе вейвлет-анализа;

разработка метода совершенствования динамических свойств и снижения нагруженности силовых передач машинно-тракторных агрегатов на основе структурной оптимизации путем введения пассивных и активных дополнительных связей.

Данные задачи были рассмотрены на примерах исследования динамической нагруженности силовых передач агрегатов: трактора ЛХТ-55 с плугом, трактора-бульдозера Т-4П (экспериментального) и трактора ДТ-75Б с орудием МДН-3 и ЩДМ-1.

Первоначальным этапом исследования динамической нагруженности силовых передач машиннотракторных агрегатов является построение математических моделей и оценка динамических характеристик.

Динамические модели машинных агрегатов с пассивными и активными рабочими органами в линейном приближении могут быть представлены в виде цепочной и разветвленной крутильно-колебательных систем с n массами, имеющими моменты инерции J k и соединенными безмассовыми жесткостями C k , при случайных возмущениях P k (t) и демпфирующих силах с коэффициентами демпфирования b k (t) [1].

По разработанным динамическим схемам представляются математические модели в виде систем дифференциальных уравнений с постоянными коэффициентами, по которым могут быть найдены передаточные функции и оценены амплитудно-частотные характеристики (АЧХ) (авторами разработан алгоритм и составлены программы). Например, из расчетов АЧХ для лесохозяйственного агрегата на базе трактора ЛХТ-55 с пассивным рабочим органом при его движении на первой передаче существенные амплитуды колебаний наблюдаются в области собственных частот, причем колебания от движителей распространяются по всей трансмиссии и доходят до первичного вала коробки передач, а от газовых и инерционных сил двигателя – значительно снижаются по амплитуде. Анализ динамики десятимассовой модели силовой передачи лесомелиоративного агрегата в составе трактора ДТ-75 Б с активным рабочим органом ЩДМ-1 представлен на графике АЧХ (рис. 1).

Следует отметить, что разработанный метод оценки амплитудно-частотных характеристик позволяет наблюдать в диалоговом режиме с компьютером изменения динамических свойств, варьируя теми или иными конструктивными параметрами и зная частотные режимы основных возмущающих воздействий.

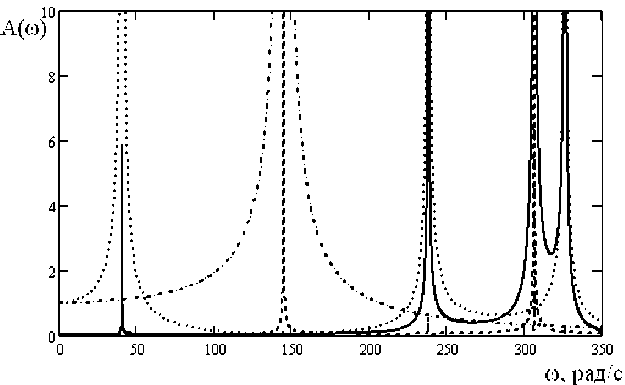
Рис. 1. АЧХтрансмиссии ДТ-75 с орудием, имеющим активный рабочий орган (ЩДМ-1). Воздействия: от фрезы на вал сцепления (—); от фрезы на ВОМ (••••); от двигателя на фрезу (-----); от фрезы на КПП (-•-•-)

Следующим этапом исследования динамической нагруженности силовых передач является анализ и оценка динамических характеристик экспериментальных нестационарных тензометрических процессов нагруженности силовых передач.

Преобразование Фурье давно и с успехом применяется для оценки статистических характеристик нагруженности (корреляционных функций, спектральных плотностей и др.) как стационарных, так и нестационарных случайных процессов динамики с применением методов сглаживания, фильтрации, усреднения и т.д. Работа современных МТА в основном состоит из переходных процессов, представляющих собой нестационарные случайные процессы. Одним из путей более полного исследования нестационарных динамических процессов нагруженности являются методы вейвлет-анализа.

В отличие от преобразования Фурье результатом вейвлет-преобразования является двумерная функция амплитуд V(а,b), где a – временной масштаб (частота), b – временная локализация и представляет собой (частотно-) масштабно-временной спектр, который дает информацию об эволюции относительного вклада составляющих воздействий разного масштаба (частот) во времени. Непрерывное вейвлетное преобразование представляется в виде свертки

+от

V(a,b) = j x(l)w'Lb(l)d t,

-от где x(t) – случайный процесс;

V a,b^(t)        ^ 0

a

[—1V a ;

– двухпараметрическая вейвлетная функция, получающаяся из ба-

зисного (материнского) вейвлета vo(t). Для примера приводятся расчеты вейвлет-спектров случайных про- цессов нагруженности (рис. 2) элементов силовой передачи трактора-бульдозера Т-4П на основе базисного вейвлета “мексиканская шляпа”.

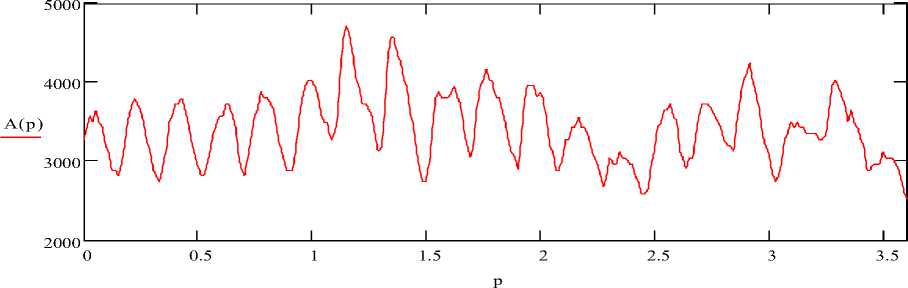
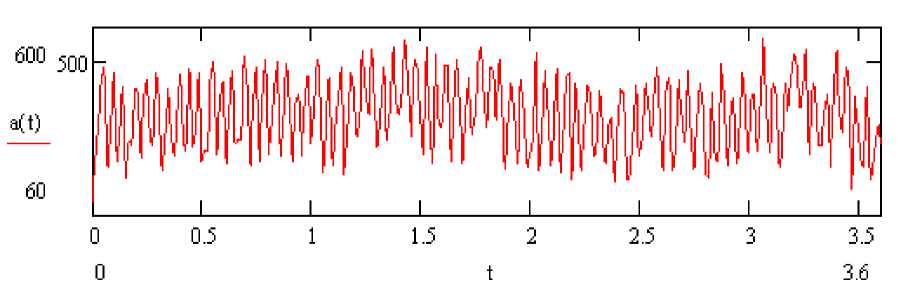
Рис. 2. Осциллограммы крутящего момента А(р), Нм на полуоси трактора и крутящего момента a(t), Нм на валу муфты сцепления трактора (t, р - время, с)

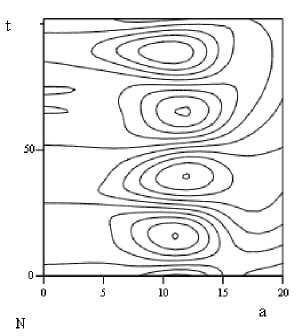
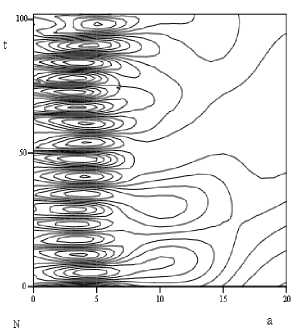
В результате расчетов в системе MathCad получены соответственно вейвлет-спектры (рис. 3), где t – время, а – масштаб (обратная величина частоте и для каждого базисного вейвлета находится по определенной зависимости).

Сравнивая вейвлет-спектры с осциллограммами, можно наблюдать изменения частоты колебаний с течением времени для данных случайных процессов, поведение различных частотных воздействий в зависимости от времени. Так, например, частота от гусеничного воздействия в начале внедрения отвала в грунт падает, затем снова возрастает, появляются низкочастотные воздействия от сопротивления грунта, которые растут по частоте.

а                              б

Рис. 3. Вейвлет-спектры случайных процессов на полуоси (а) и на валу муфты сцепления (б)

Интересно отметить, что изменения частоты от полуторной гармоники двигателя коррелируют с изменениями частоты гусеничного воздействия и сопротивления грунта. Следует отметить, что таких характерных изменений мы не смогли бы наблюдать по характеристикам Фурье преобразования [2].

Описанная методика позволяет установить распределение амплитуд колебаний в зависимости от частоты и времени, установить временную зависимость амплитудно-частотных характеристик процесса.

Третьим этапом исследования динамической нагруженности силовых передач является совершенствование динамических свойств и характеристик.

Среди основных направлений повышение надежности и долговечности силовых передач и оптимизации динамических свойств можно выделить два:

выбор оптимальных конструктивных параметров силовой передачи (параметрическая оптимизация); рациональный выбор структуры силовой передачи (структурная оптимизация).

Структурная оптимизация рассматривается в направлении снижения динамических колебаний на основе методов вибротехнологий путем введения пассивных и активных дополнительных связей систем виброзащиты и виброизоляции.

Рассмотрим АЧХ многомассовых систем при введении дополнительных связей при силовом и кинематическом воздействии на систему (рис. 4).

Система уравнений с введенной дополнительной связью в виде одномассовой цепи с_п- 1 - J_n+1 - с_п+2 имеет вид

••

J 1 • x i + c 1 ( x 1 - x 2 ) — M g ( t ),

...........................................,

••

J -Xn + c ,(x ,—x } + c (x — x^} + c^,(x —x ^,} + c„(x — x„} = 0, is n nn > n--1 уn— -1 пП/ nV n n + 2/ n + 1 V n n + 1/ П П Vn n Пц/ ,

••

J 1 J 2

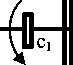
М д

^J n + 1 • x n + 1 ⁺ c n + 1 ⁽ x n ^- x n + 1 ) ⁺ c n + 2 ⁽ x n + 1 ^- x n + 2 ) = F e ⁽ t ),

••

J n + 2 • x n + 2 + c n ⁽ x n ^- x n + 2 ) ^- c n + 2 ⁽ x n + 1 ^- x n + 2 ) = ^M c ⁽ t )•

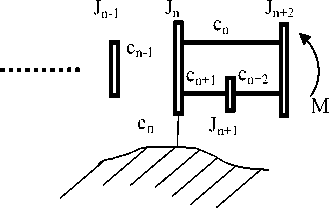
Рис. 4. Динамическая модель с учетом дополнительных связей при силовом и кинематическом воздействии на систему

На примере шестимассовой модели трансмиссии ЛХТ-55, с введенной дополнительной связью, передаточные функции виброизоляции силовой передачи от сил технологического сопротивления Мc(t) на вал муфты сцепления имеют вид

W i 7 ( iw ) = -^ 1-

1 7 M_c

^x 1 - ^x 2

Mc

A 7 1 - A 7 2

А

где A 7 1 = « 1 • a 2 • a 3 • a 4 ( a 6 • a 7 - d 6 • a 5 ),

A 7 2 —— d 1 • a 2 • a 3 • a 4 ( a 6 • a 7 — d 6 • a 5 ) ,

*

А — D j 4 • D 5 7 - a 4 • D j 3 • D 6 7 ;

D *5 7

d ₅ a ₆ a ₅

a ₆ d ₆ a ₇

a ₅ a ₇ d ₇

D 6

d ₆

a ₇

d ₇

Можно рассмотреть нули передаточной функции, приравняв числитель к нулю, и тем самым определить частоты и режимы динамического гашения колебаний.

A7 i — A7 2 = 0, т.е. (a^ + dj) • a2 • a3 • a4(a6 • a7 — d6 • a5) = 0.

Рассмотрим нахождение передаточных функций виброзащиты от микропрофиля при введении пассивных динамических связей (жесткостных или демпфирующих) на участке J тр - с п - х п ( J тр – момент инерции подвески, с п – жесткость грунта). Передаточная функция виброзащиты от воздействия микропрофиля x п на вал муфты сцепления имеет вид

W 5 ( iw ) = "  cx nn

A 51 - A5 2 = (d 1 + a 1) • a 2 • a 3 • a 4 • d 6

A ~        D , 6

где A = D 1

6 =

d ₁ a ₁

a ₁

d2

a2  d3

a3

a5

a5

Рассмотрим разветвленную схему с приводом активного рабочего органа при введении дополнительных связей на месте сцепного устройства с агрегатируемым орудием (рис. 5).

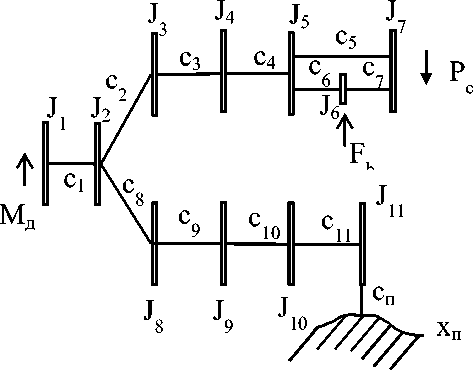
Рис. 5. Динамическая схема с приводом активного рабочего органа при введении дополнительных связей

Вышеупомянутыми разработанными методами нахождения передаточных функций в зависимости от конструктивных параметров могут быть найдены АЧХ от различных воздействий. Например, АЧХ виброизоляции от воздействия фрезы на вал муфты сцепления находится

^W 1 7⁽ iw ) = ^ A = A = D *1 7 • D ,

^A 7 3

-

( d₁ + a ) - a., • a₃ -a

_{A 7 4}          1       1      2 3     4

•

A                 A

„ — a 2 D 1 • D *3 7 • D 9 „ , D *1 7 = D 4 • D

D *3

7 = D 3 4 • D *5 7 — a 4² • D 3 3 • D 6 7 , D .5 7 =

d a a

a d

a ₅

a ₇

• D 8 11

,

a d a

—

^a 4 ^D1 3 ^D 6 7 ,

a a d

,

d k     a k + 1

a k + 1    d k + 1    a k +2   ........

D k

.... .... .... ........

.... .... .... ........

an  dn

Варьируя параметрами введенной одномассовой цепи c 6 , c 7 , J 6 и управляя вибрационным воздействием F в (t), можно добиться оптимизации динамических свойств.

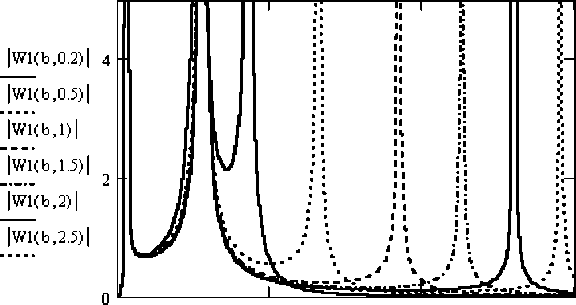
На основе данных исследований был проведен ряд расчетов по изучению динамических свойств и характеристик трактора-бульдозера Т-4П при введении дополнительных связей. При увеличении параметра жесткости сцепного устройства третья собственная частота растет и значение амплитудно-частотной характеристики падает в диапазоне частот от 30 рад/с и выше (рис. 6). В области первых собственных частот АЧХ остается без изменения.

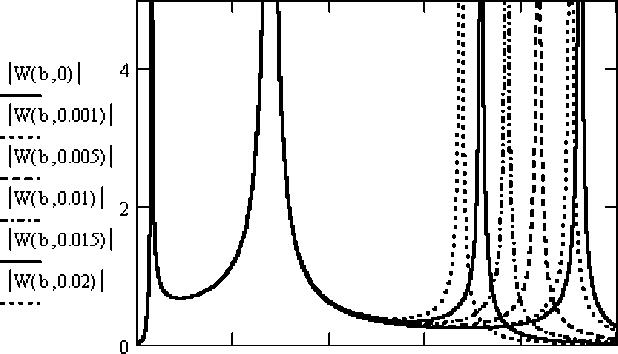
При введении дополнительной пассивной связи с передаточной функцией L(p)=mp² изменения АЧХ при варьировании параметра массы m представлены на рисунке 7. Как видно из рисунка, третья собственная частота уменьшается, а первые частоты остаются без изменения и АЧХ меняются в соответствии с изменениями собственных частот.

0                     50                    100                , 150

b

Рис. 6. Изменения АЧХ / W(b,i) / от сил сопротивления до силовой передачи с увеличением жесткости сцепного устройства (b – частота, рад/с, i – коэффициент увеличения жесткости)

0         20         40         60 SO 100

ъ

Рис. 7. Изменения АЧХ / W(b, m) / от сил сопротивления до силовой передачи с увеличением массы дополнительной пассивной связи

Введение активных дополнительных связей даже с одномассовой цепью и дополнительным вибрационным воздействием приводит к обилию расчетов из-за большого количества вариантов цепи. Поэтому в данной работе приведем только один из частных случаев. На рисунке 8 приведены результаты расчетов вынужденных колебаний при синусоидальном воздействии на агрегат определенной частоты и амплитуды. Расчеты показывают, что наибольшее снижение колебаний силовой передачи наблюдается при равенстве частоты вибрационного воздействия частоте воздействия на агрегат.

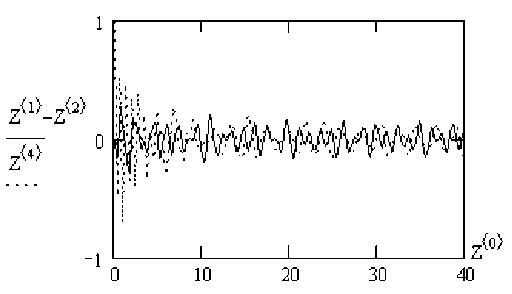
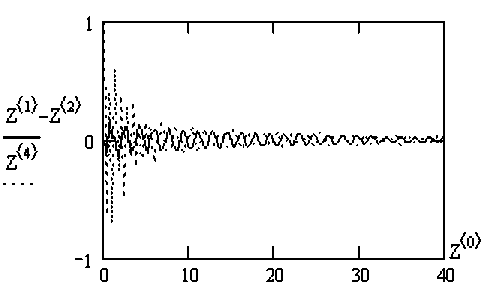
б

а

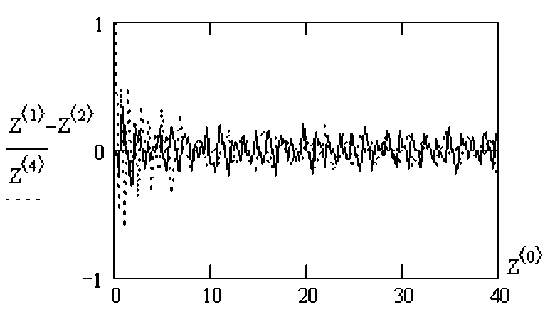
в

Рис. 8. Колебания системы (амплитуды колебаний силовой передачи — , агрегатируемого орудия — ): а - без вибрационного воздействия; б - частота вибрационного воздействия равна частоте P c ; в - частота вибрационного воздействия не равна частоте P c

Выводы

• 1.    Разработанный метод построения математических моделей динамики силовых передач МТА и нахождения динамических характеристик позволяет выявить изменения динамических свойств в зависимости от внешних воздействий и конструктивных параметров.

• 2.    Предлагаемый метод оценки статистических характеристик динамических процессов силовых передач на основе вейвлет-анализа позволяет установить частотно-временной спектр нагруженности.

• 3.    Разработана методологическая основа совершенствования динамических свойств силовой передачи путем введения активных и пассивных дополнительных связей (в виде различных динамических устройств, пружин, демпферов и др.) методами структурной оптимизации.

Таким образом, реализовывается основной принцип построения модели, более адекватной реальному объекту, на основе априорной и апостериорной информации и корректировки (совершенствовании) структуры и параметров объекта.