Моделирование и оптимизация иерархических структур управления

                                         том 21 № 1 (66), 2025, ст. 1

В различных экосистемах участники организуются в иерархические структуры. Наиболее яркие примеры – армия, органы государственной власти, коммерческие фирмы. Эволюционно образование иерархий с множеством связей присуще более сложным системам и наиболее оптимально для эффективного существования/выживания.

Выпадение из структуры какого-либо исполнителя или ослабление связи приводит к разрушению цепочек управления, хаосу. При возникновении такой ситуации организации стремится заменить выпавшее звено, создать новые связи, новую иерархию управления. Т.е. принять форму, позволяющую восстановить управляемость.

В результате непрерывных изменений могут создаваться «нежизнеспособные» структуры или отдельные фрагменты структур, когда в какой-либо ветке управления появится исполнитель или исполнители, существенно ухудшающие способность организации, что, в свою очередь, например, для бизнеса в условиях конкуренции, приведёт к гибели этой «нежизнеспособной» организации или ветки управления.

При наличии набора из одних и тех же исполнителей выстраивание их в различные управляющие структуры, реинжиниринг позволяют, как будет показано ниже, добиваться существенного изменения эффективности организации в целом.

Важным фактором, влияющим на структуры, является развитие технологий, вычислительных мощностей, появление автоматизированных систем, способных заменять в процессах, организационной иерархии человека или отдельные подсистемы [1]. При этом способности подобных автоматизированных систем всё более и более приближаются к возможностям человека, а где-то существенно начинают их превосходить.

Для обеспечения своей конкурентоспособности организации вынуждены непрерывно пересматривать свои бизнес-процессы, более осознанно изменять свою структуру управления.

Состояние изученности предметной области

Акцент изученности предметной области делается на рассмотрении организации как набора процессов и управляющей структуры, включающей в свой состав как людей, так и механизированные, автоматизированные, роботизированные системы. Общий тренд - передача функций от человека-исполнителя к компьютерам. Исходя из этого подхода изученность предметной области рассматривается от работ по управлению персоналом, командами и заканчивается описанием архитектурных паттернов построения автоматизированных систем.

Основоположником тектологии, или «всеобщей организационной науки», научной дисциплины, считается российский учёный А. Богданов. Работа А. Богданова "Тектология. Всеобщая организационная наука" [2] представляет собой исследование принципов организации и управления в различных сферах деятельности и природы. Тектология рассматривает управление организацией как универсальный процесс, применимый к различным уровням иерархии- от простейших систем до сложных социальных и производственных структур. В контексте организационной иерархии управления, Богданов выделяет несколько ключевых аспектов: принципы организации, иерархию, связи, взаимосвязи между элементами системы, управление как процесс. Связи и управляющие структуры могут создаваться и распадаться. Положительный отбор увеличивает сложность связей, увеличивает разнообразие в природе. Важным аспектом работы является А. Богданова понимание управления не как статического процесса, а как динамичной системы, требующей постоянного анализа и адаптации к изменяющимся условиям. А. Богданов считал, что иерархия необходима для создания четкой структуры управления. Каждый уровень иерархии выполняет свои специфические функции, что позволяет распределять задачи и ответственность. Это помогает избежать путаницы и дублирования усилий, а также обеспечивает более эффективное использование ресурсов. Богданов подчеркивает важность связи между различными уровнями иерархии. Эффективное управление требует хорошей коммуникации. Оптимизация всех процессов внутри системы включает в себя устранение избыточных уровней управления, сокращение времени на принятие решений, улучшение качества взаимодействия между различными подразделениями.

М. Хаммер дал развитие направлению Business process reengineering. В своих исследованиях [3] он дает определение реинжинирингу как коренной перестройке процессов организации. Частичные улучшения требуют тонкого, деликатного подхода, а существенные улучшения достигаются только путем решительного отсечения всего старого, отжившего и замены его на новое и жизнеспособное. М. Хаммер делит организации на три вида. Первые - это те, кто вынужден делать реинжиниринг ввиду фактического банкротства. Вторые - чей топ менеджмент видит в ближайшей перспективе неизбежные перемены и заранее проводит реинжиниринг, чтобы избежать грозящих убытков. Третьи организации - это компании- лидеры, которые за счет реинжиниринга могут улучшить своё доминирующее рыночное положение. Реинжиниринг по М. Хаммеру стоит проводить в случаях, когда планомерные и минимальные изменения существующих процессов не дают желаемых результатов. М. Хаммер указывает, что информационные технологии сами по себе не меняют плохо выстроенные процессы. Одновременно с этим информационные технологии могут являться мощнейшим инструментом для реализации целей реинжиниринга.

В исследовании С. Хамфри [4] приводится анализ эффективности различных команд. Команды имеют иерархию, при которой часть входных сигналов распределена и обрабатывается между исполнителями низших командных уровней. Сложность иерархии будет определяться количеством обрабатываемых командой входных сигналов. Используется термин «длинный канал связи», что может приводить к «зашумлённости» передаваемого сигнала и к выработке неточного управленческого решения. Выработка качественного решения рассматривается как вероятностное, зависящее от множества факторов и, в итоге, определяющее эффективность всей команды в целом. В работе в т.ч. проводится оценка эффективности коммуникаций лично между сотрудниками, либо через компьютер.

Гринько Т.В. [5] отмечает, что реализация концепции Business Process Reengineering предполагает интенсивное использование экономико-математических моделей и информационных технологий и приводит примеры решения подобных задач.

В работе М. Губко [6] организация рассматривается как оптимальный с экономической точки набор управляющих менеджеров над фиксированным множеством исполнителей. Оптимизация иерархии управления производится исходя из наименьшей стоимости организационной структуры для управления исполнителями.

Г.В. Росс рассматривает построение рациональной организационной структуры с точки зрения компетенций сотрудников компании [7]. Приводятся примеры возможных математических задач оптимизации структур управления над отдельными исполнителями, технологическим процессом, группами технологических процессов. Задачи сводятся к работе с графами.

Стандарт ANS/ISA-95-3 открывает новую эру в философии контекста управления производственным предприятием и, в идеальном случае, предполагает выстраивание автоматизированных контуров, без участия человека [8]. Стандарт описывает уровни автоматизации управления предприятием, цехом, участком, технологическим оборудованием. Предлагаемый взгляд на иерархию и модель управления указывает, что эффективно планировать ресурсы производственного предприятия, строить планы, графики по оптимальному использованию доступных ресурсов предприятия могут и должны специализированные компьютерные системы: ERP, APS, MES, SCADA. Стандарт описывает модели, контуры объёмного и детального планирования, типовую, эталонную функциональность производственных систем и информационные потоки между ними.

В работе 4D RCS [1] рассматривается архитектурный концепт построения структуры армии будущего. Исследование предлагает архитектурные принципы разделения функций и унификации интерфейсов для гибридных иерархических систем, включающих себя как людей, так и беспилотные автономные комплексы. Цель работы - дать инженерам-разработчикам единообразные подходы и принципы построения функциональности и интерфейсов систем. Предполагается, что на верхнем уровне любой военной иерархии есть командир-человек, поддерживаемый персоналом, который обеспечивает функции разведки и поддержки принятия решений. На этом самом высоком уровне определяется стратегия и устанавливаются стратегические цели. В дереве иерархии могут присутствовать как люди, так и роботизированные комплексы, имеющие возможность действовать некоторое время автономно. Важным является выделение контуров управления стратегического, тактического и операционного уровня. Цикл перепланирования высших уровней управления будет на порядки больше циклов более низких систем автоматизации.

В работе Р. Загидуллинина [9] рассматривается организация работы производственного предприятия с использованием MES и APS систем. Предприятие описывается как набор мощностей - рабочих центров, обладающих возможностью выполнять те или иные операции с той или иной производительностью. Для выполнения операций и получения готовой продукции требуются ресурсы: материалы, персонал. Чтобы получить тот или иной готовый продукт создаются технологические карты с требуемыми последовательностями операций. Операции могут выполняться на различных рабочих центрах. Задача модуля планирования MES или APS системы - предложить варианты планов, наиболее эффективным образом использующих производственные ресурсы, персонал, материалы. Система планирования должна позволять формировать несколько вариантов производственных планов с различными результирующими ключевыми показателями эффективности. Целевая функция может учитывать множество ключевых показателей эффективности. ERP и APS системы осуществляют объемное, календарное планирование, система MES - детальное планирование и графикование. Управление и планирование рассматриваются как формализованная математическая задача, которую выполняют ERP, APS и MES системы. Подходы, заложенные в работе Р. Загиддулина, можно использовать не только для производственного предприятия, но и, в принципе, для любой организации, работу которой можно описать в виде отдельных операций, цепочек операций, технологических карт, ресурсов.

С.М. Соколов в своей работе [10] указывает что в опытно-конструкторских работах в соответствии с имеющимися тенденциями должны быть реализованы интеллектуальные программно-алгоритмические средства, позволяющие обеспечить интеграцию разнотипных роботов в единую группу с последующим управлением их совместными действиями, а также интеллектуальные системы человеко-машинного интерфейса и поддержки принятия решений операторами управления. Также в исследовании С.М. Соколова указывается одной из самых сложных проблем при оценке и проведения сравнений автономности беспилотных средств – это определение/установка модели уровня автономии для конкретной предметной области для выбранных программ.

В работе И. Решетникова и И. Кораблева [11] приводится методика аудита по шаблону “контекстной функциональности” для анализа текущего уровня автоматизации производственного предприятия исходя из моделей систем класса MES/MOM [8]. Делается предположение о том, что любая операция будет выполняться эффективнее, если эту операцию будет выполнять не человек, а автоматизированная система, компьютер. Исходя из этой логики поиск гэпов в бизнес-процессах будет происходить нахождением операций, выполняемых в ручном режиме. Используя предлагаемую числовую шкалу, можно проводить аудит процессов предприятия до и после проведения проектов по автоматизации.

В работе [12] предполагается, что операции могут выполнять как человек, так и автоматизированная система. Для перехода к максимально автономному производству требуется контроль- авторизация операций, измерение и журналирование уровня автоматизации операций. Операции, выполняемые человеком, могут говорить о потенциальных проблемах, о вмешательстве в процесс человека. Чем чаще операция выполняется компьютером, без человека - тем выше общий уровень автоматизации производства. Цель непрерывного аудита организации - отследить и уменьшить человеческий фактор.

Постановка задачи

Целью данной работы является моделирование исполнителей и их связей, повышение эффективности организации за счёт:

• •    оптимальной расстановки исполнителей с различными характеристиками;

• •    введения в структуру управления «суперисполнителей» (цифровых помощников, автоматизированных/роботизированных систем);

• •    поиска зависимостей, оптимального места для различных исполнителей в иерархии управления;

• •    использования удобного инструмента для визуализации, сравнения иерархических структур, построенных программой- оптимизатором.

Для определения целевой функции используется концепт Джона Бойда, описавшего цикл управления OODA [13]. В качестве одного из основных факторов победы Бойд выделил способность организации быстрее, нежели чем конкуренты, совершать цикл OODA, т.е. реагировать на изменения внешних условий или действия конкурентов. Скорость реакции организации на изменение, скорость её управляемости может рассматриваться как один из ключевых показателей эффективности при формировании организационной структуры.

Ограничения и допущения

Используемые далее модели и характеристики исполнителей могут, в общем случае, быть применимы как для людей, так и для автоматизированных/роботизированных систем. Принимается допущение, что каждый исполнитель имеет только один вышестоящий в иерархии узел управления и не взаимодействует с множеством других управляющих узлов. Все исполнители взаимозаменяемы и могут занимать любое место в иерархии управления. В характеристиках исполнителей упускаются такие их способности как контекстная функциональность для выполнения той или иной задачи.

Исполнителей, не имеющих в иерархии управления «подчинённых» будем называть терминальными. В практических задачах автоматизации в качестве терминальных узлов, исполнительных механизмов могут выступать устройства, физически не имеющие возможность взаимодействовать с другими узлами. Это, например, такие устройства как электродвигатель или информационное табло. Такие устройства работают только на получение управляющей информации, т.е. могут быть только терминальными. Такое представление отчасти может быть применимо и к людям, не имеющих способности коммуницировать с другими людьми. Например, человек, условно, может быть очень сообразительным, но абсолютно замкнутым.

Упрощение представления исполнителей состоит также в «свёртывании» их внутренних характеристик. Джон Бойд выделил четыре ключевых операции для исполнителя: сбор информации (observe), обработка информации (orient), выработка решения (deside), выполнение действия (act), сокращённо - цикл OODA [13]. Для решения задачи оптимизации иерархии все четыре операции OODA сведены к одной общей способности исполнителя - «сообразительности» (smartness), измеряемой в секундах. Т.е. для задачи построения дерева иерархии исполнитель представляется как «черный ящик», имеющий время обработки и передачи информации, без детализации внутренней структуры, внутренних операций этого исполнителя.

Более полные характеристики исполнителей и автоматизированных систем, такие как контекстная функциональность, автономность и способы измерения этих характеристик даны в работе [14].

Упрощением при постановке задачи также является отсутствие и расчёт в модели контуров обратной связи, использующихся в теории автоматизации. Рассматривается только прямое распространение информации, сигнала от «центра управления» до исполнителя, без получения обратной связи. Данное упрощение справедливо для практических задач, когда используется один и тот же канал связи выдачи управляющего воздействия и получения обратной связи от исполнителя, обычно, с одной и той же скоростью. Т.е. скорость распространения информации от центра до исполнителя, обычно, будет равна на практике скорости обратной связи -информации от конечных, терминальных исполнителей до центра.

Задача 1. Оптимизация иерархической структуры управления

Количество исполнителей (Executors), которых необходимо включить в единую иерархическую структуру, обозначим как n . Имеем множество исполнителей - Е_; , где i 6 {1,2,..., п} .

Передача информации от одного исполнителя до другого всегда требует времени, при этом исполнители не равноудалены друг от друга. Расстояние от исполнителя i до исполнителя j обозначим как L ij , где i 6 {1,2,3,...n},j 6 {1,2,3,...n} . Будем измерять расстояние между исполнителями в секундах.

Ограничением для построения иерархии может служить отсутствие пути (отсутствие возможности передачи информации) от исполнителя i до исполнителя j. В контексте построения иерархии управления величины Lij могут считаться характеристиками узлов i и j. Одни исполнители могут находиться в «гуще» связей и иметь короткие пути до множества соседних исполнителей, другие узлы могут быть сильно отдалены от других узлов, что неизбежно повлияет на их место в иерархии управления. Географически можно представить отдалённых исполнителей как находящихся в разных «городах», и, соответственно, построение оптимальной иерархии управления будет учитывать этот фактор.

Часть исполнителей могут иметь только входящие маршруты «до» этого исполнителя, и не иметь маршрутов «от» этого исполнителя, что позволит включать данного исполнителя в иерархию только как терминальный узел.

С точки зрения теории графов исполнители E_t представляют из себя вершины, L ij - рёбра. Обозначим граф всех вершин и связей как G(E, L).

Для описания исполнителей введём следующую их характеристику - «сообразительность». Будем рассматривать «сообразительность» как суммарное время приёма, обработки исполнителем полученной информации, выработки планов с декомпозицией задач и действия, выраженного в передаче информации последующим узлам или действия над объектом управления, если узел терминальный. По сути «сообразительность» – это инертность узла в передаче информации, от момента получения данных до момента действия этого узла. Обозначим «сообразительность»(smartness) как S_t , где i 6 {1,2,3, .,п} . «Сообразительность» узлов будем измерять в секундах.

Введём для исполнителей ещё одну характеристику - «коммуникабельность». Будем использовать «коммуникабельность» как ограничение и способность исполнителя образовывать связи для обмена информацией с другими исполнителями. Для человека, например, фактическая способность «коммуникабельности» лежит в пределах от 6-ти до 9-ти. Т.е. средний человек, руководитель, может при личном контакте нормально управлять 6-ю…9-ю исполнителями.

Обозначим характеристику «коммуникабельность» исполнителя (ability communicate) как как C_t , где i 6 {1,2,3, .,п} .

Узлы, не имеющие способности коммуницировать с другими узлами с C_t = 0 могут выступать в дереве иерархии только как терминальные.

Последним элементом, необходимым для моделирования задачи служит команда руководителя, событие Start, на которое организация должна отреагировать. Событие Start возникает в момент времени t=0 .

Событие Start можно включить в граф G как дополнительную вершину. Дадим этой вершине условный номер 0. С учётом условия, что каждый исполнитель может занимать любую позицию в иерархии – это будет означать что от узла Start будет возможен путь распространения информации до каждого исполнителя - L₀ j , где j 6 {1,2,3,..., п} .

Время, через которое первый узел в иерархии j отработает событие Start будет равно L\j = L₀ j + S j Для простоты можно принять, что время реакции первого исполнителя на вершине иерархии будет сдерживаться только его «сообразительностью», т.е. он сам принимает решения на основании события Start, т.е. L₀ j = 0 .

Событие Start получает только один исполнитель. Таким образом можно для данной вершины Start проставить параметр «коммуникабельность» С₀ = 1 .

Преобразуем граф G(E, L) в G'(E', L') путём добавления в него вершины Start .

Ребра L ij графа G можно трансформировать в L j где L ^j = L ij + S j , где i 6 {0,1,2,3,...n},j 6 {0,1,2,3,... n} . Такое преобразование можно представить следующим образом - исполнитель i , имеет видимый объект управления и промежуточного исполнителя j . Для того, чтобы оказать воздействие на объект требуется время на передачу управляющей информации L ij до исполнителя , а также время на «обдумывание» этим исполнителем j поступившей к нему информации - S j .

Задача оптимизации сводится к поиску оставного дерева графа G'(E',L') со стартовой вершиной Start и учётом ограничения по коммуникабельности узлов C .

Для построения дерева иерархии в RStudio во всех последующих примерах использовался пакет Analyses of Phylogenetics and Evolution (APE) [15]. Параметры n, S, L, C , выбирались случайным образом, с равномерным распределением.

Пример 1. Простейшее дерево иерархии

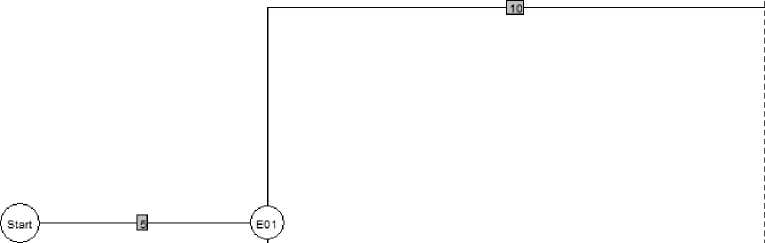
Пусть есть три исполнителя n=3. Первый в иерархии исполнитель i=1 с сообразительностью S 1 = 5 , к которому подключаются два других исполнителя: второй i=2 с сообразительностью S₂ = 7 , расстоянием L₁₂ = 7 и третий, исполнитель i=3 с сообразительностью S₃ = 1 , расстоянием L₁₃ = 9 . Графическое изображение такого дерева иерархии показано на рис.1.

Иерархия управления. Т_тах = 15сек п=3, С={2. 5), S={1 .7}. L={1 .70}

---------------------------О---------------------------- Еог |

I                                                I                                                I                                                I                                               I                                                I                                                I                                                I                                               I                                                I                                                I                                                I                                               I                                                I                                                I                                                I

О       1       2       3       4       5       6       7       8       9      10      11      12      13      14      15

Time, s

Рис. 1. Простейшее дерево иерархии для трёх узлов

На рис. 1 в момент времени 0 s происходит начальное событие «Start». Исполнитель i=1 (Executor) «E01» показан в круге, т.к. он не является терминальным. Исполнители «E02» и «E03» являются терминальными (не имеют подчинённых узлов). Событие «Start» воспринимается исполнителем E01 через интервал времени L ₀ = 5 1 = 5 секунд и будет передано двум последующим исполнителям 2 и 3. Исполнитель E02 отработает управляющее воздействие через ^ 12 = ^ 12 +5 2 = 7 + 1 = 8 секунд. Исполнитель E03 отработает управляющее воздействие через ^ 13 = ^ ₁₃ + 5 3 = 9 + 1 = 10 секунд. Величины 5, 8, 10 показаны на графике как длины ветвей, в серых прямоугольниках. Максимальное время, в течении которого все исполнители структуры отреагируют на внешнее воздействие будет определяться самой длинной ветвью дерева (цепью вершин и рёбер). Максимальное время выделено на графике красной штрихпунктирной линией, ^Тт_ах = ^ 0,1 ⁺ Ч3 = ^{5 + 10} = ¹⁵ секунд.

В формате Newick описание дерева на рис.1 будет выглядеть как строка: «((E03:10,E02:8)E01:5)Start;» [15].

В качестве параметра для оценки эффективности организации принимается время реакции структуры на изменение - T _max .

том 21 № 1 (66), 2025, ст. 1

Задача оптимизации будет сведена к поиску оставного дерева графа G' с минимальным времени Tmax с учётом ограничений.

Пример 2. Управляющая структура для n=100 исполнителей

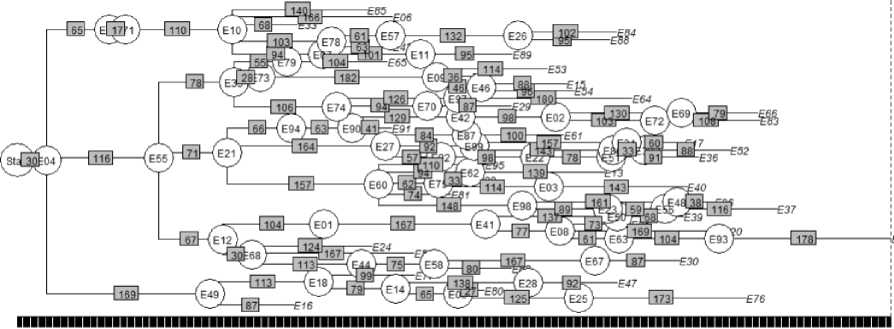
Есть n=100 исполнителей, со случайно распределёнными «сообразительностью» 1 <= 5 j < = 100 , «коммуникабельностью» 1 <= С ; <= 6 и матрицей расстояний между узлами 1 <= L ij <= 100 . Дерево иерархии для таких заданных условий составленное случайным образом без оптимизации может выглядеть так, как показано на рис.2 с временем реакции T_max = 904 с.

Иерархия управления. Т_тах = 904 сек п=100, С=(1...6}, S={1...98}, L={1 -100}

0 20 43 66 89 115 144 173 202 231 260 289 318 347 376 405 434 463 492 521 550 579 608 637 666 695 724 753 782 811 840 869 898

Time, s

Рис. 2. Дерево иерархии не оптимизированное, 7_тах = 904 с

Пример 3. Оптимизированная управляющая структура для n=100 исполнителей

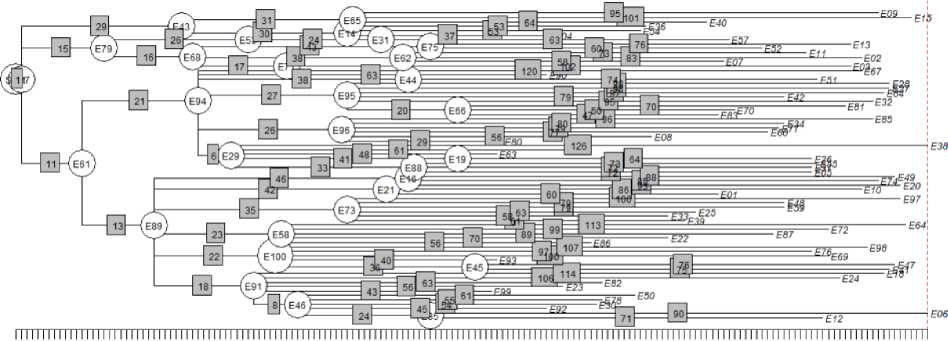
Для того же набора исполнителей из примера 2 дерево иерархии может быть оптимизировано с использованием подходов дискретной математики и выглядеть так, как показано на рис. 3.

В примерах 2 и 3 для одних и тех же исполнителей с одинаковыми характеристиками построенные из этих исполнителей иерархии без оптимизации и с оптимизацией различаются по эффективности почти в 5 раз. Безусловно, на практике большая часть орг. структур уже является оптимизированной, т.к. в противном случае такие организации не смогли бы конкурировать. Пример 3 показывает возможность применения компьютерной оптимизации уже существующих структур. Оценочно, на практике оптимизация структуры, выполненная компьютером, будет превышать эффективность организации, составленной человеком не менее чем на 3-5%.

том 21 № 1 (66), 2025, ст. 1

Иерархия управления. Т_тах = 165сек гг 100, О{1 ...6}, S-{1 ...98}, L={1.100}

0 3 6 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 93 97 102 107 112 117 122 127 132 137 142 147 152 157 162

Time, s

Рис. 3. Дерево иерархии оптимизированное, Г_тах = 165 с

Пример 4. Изменение характеристик для 100 исполнителей

Цель примера 4 – показать различные «рисунки» иерархического дерева при задании различных начальных характеристик исполнителей. «Сообразительность», расстояния между исполнителями, на практике могут меняться, могут быть случайными величинами или могут определяться некими факторами, такими как географическим расположением исполнителей, что может объединять исполнителей по «группам» или по «уровням» управления.

Иерархия управления. Т_тах = 308 сек п=100 С={1 6} S={25 75} I -{25 75}

О в 13 21 29 37 45 53 01 09 77 85 93 102 112 122 132 142 152 162 172 182 192 202 212 222 232 242 252 262 272 282 292 302

Time s

Рис. 4. Дерево иерархии для 100 исполнителей с изменёнными параметрами S и L

том 21 № 1 (66), 2025, ст. 1

В примере 4 даны n=100 исполнителей, со случайно распределёнными «сообразительностью» 25 <= S i <= 75 , «коммуникабельностью» 1 <= С ^ <= 6 и матрицей расстояний между узлами 25 < = Lij <= 75 . По сравнению с примером 3 диапазон случайных величин для параметров S и L сужен. Дерево иерархии для таких условий может выглядеть так, как показано на рис.4 и визуально уже имеет выраженные «уровни» управления, присущие реальным организациям.

Задача 2. Введение в систему иерархии «суперисполнителя»

Практически очевидно, что при введении в систему исполнителя («суперисполнителя») с характеристиками, существенно превышающими средние характеристики других исполнителей положение такого суперисполнителя будет стремиться к вершине иерархии. Как будет показано ниже это также подтверждается корреляционными зависимостями.

В набор из 100 исполнителей, использовавшихся в примерах 2 и 3, для исполнителя i=50 изменим (улучшим) его параметры «коммуникабельность» и «сообразительность» до максимально возможных S50 = 1, С50 = 99

Результат работы оптимизатора показан на рис.5. «Суперисполнитель» E50 занял самое высокое место в иерархии при этом время реакции системы на событие Start уменьшилось до Tmax = 137 сек.

Иерархия управления. Т_тах = 137 сек п=100, С={1. 99}. S={1 .98}. L={1.. 100}

О 3 6 9 12 16 20 24 28 32 36 40 44 48  52 56 60  64 68 72 76 80 84 88  92 96 100   105  110  115   120  125  130  1 35

Time, s

Рис. 5. «Суперисполнитель». Для исполнителя i=50 заданы «коммуникабельность» и «сообразительность», 5_S o = 1, С₅₀ = 99

том 21 № 1 (66), 2025, ст. 1

Таким образом, в целом, изначальные данные и ограничения могут предопределять место исполнителя в иерархии управления.

Например, как уже было сказано выше, исполнитель i с коммуникабельностью Q = 0 не сможет иметь связи с нижестоящими уровнями иерархии и поэтому способен занимать только «терминальное» положение, быть конечным узлом в цепочке управления. На практике в нижнем уровне автоматизации Level 1 [8] терминальными всегда будут являться исполнительные механизмы (электропривод, звуковая, световая сигнализация, ...) и датчики (термопары, сенсоры, выключатели, ...).

Другим видимым ограничением для узлов может быть наличие/отсутствие связей с другими узлами L ij . Очевидно, что для узла i даже при отсутствия ограничении в коммуникабельности С_; >> 0 отсутствие связей к другим узлам L ij = NA и при наличии связей узлов k к этому узлу L_ki ^ NA сможет сделать этот узел только терминальным. И наоборот, исполнитель j , не имеющий входных связей от других узлов L_k j = NA сможет занимать только верхнюю ступень в иерархии.

Зависимости

Для примера 3 зависимость места расположения исполнителя в иерархии от его «сообразительности» показана на рис. 6. «Сообразительные» в эффективной организации располагаются выше на иерархии управления.

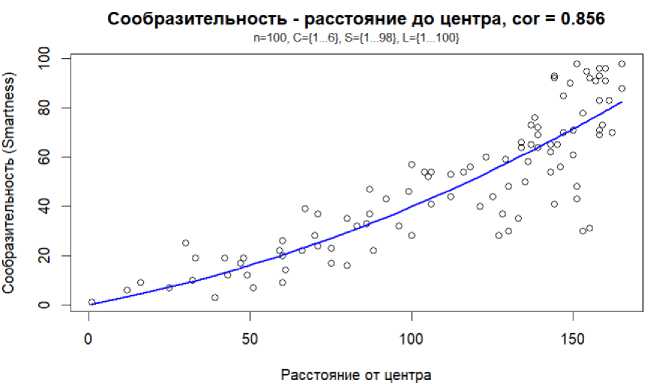
Рис. 6. Зависимость места в иерархии управления от «сообразительности»

Для примера 3 зависимость расположения в иерархии от «тяжести» исполнителя

(удалённости от других исполнителей и его собственной сообразительности) показана на рис.7.

том 21 № 1 (66), 2025, ст. 1

«Сообразительные» и «находящиеся в гуще связей» исполнители занимают в эффективных организациях более высокие места в иерархии.

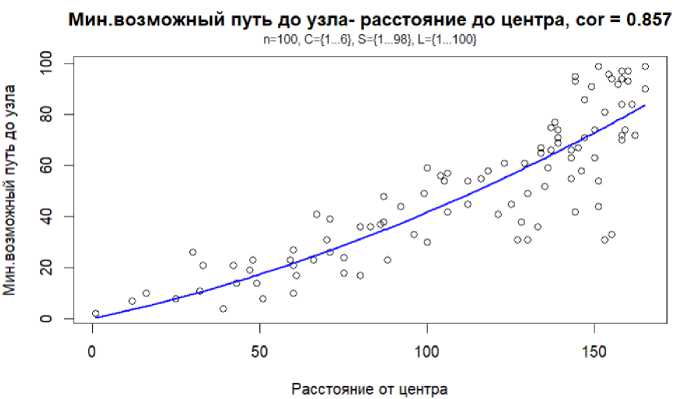
Рис. 7. Зависимость места в иерархии управления от «тяжести» исполнителя

Для параметра «коммуникабельности» в примере 3 корреляция получалась слабая, поэтому для построения явной зависимости места в иерархии от «коммуникабельности» использовался набор из 200-т исполнителей и более суженные рамки случайных величин S и L, рис. 8. «Коммуникабельные» в эффективной организации располагаются выше на иерархии управления.

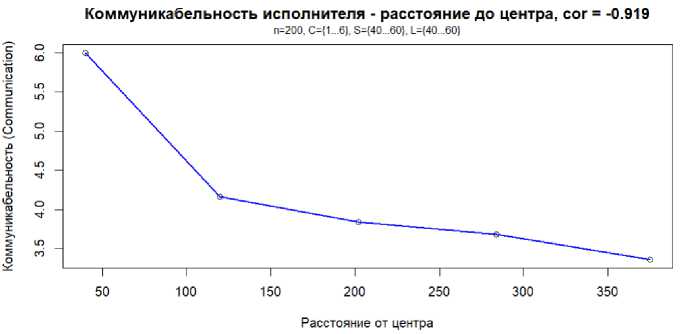
Рис.8. Зависимость места в иерархии управления от «коммуникабельности» исполнителя

NP-трудность

При ограничении «коммуникабельности» до минимального значения С, = 1 для всех n исполнителей каждый исполнитель будет иметь возможность подключаться к другому исполнителю только один раз, т.о. исполнители выстроятся в цепочку. Поиск оптимальной структуры при таком ограничении будет сводиться к задаче коммивояжёра (TSP). Задача коммивояжёра является NP–трудной, количество вариантов решений с учётом вершины Start будет равно n! При снятии ограничения «коммуникабельности» и установки для всех узлов максимального значения С = п — 1 для всех i каждый исполнитель будет иметь возможность подключения сразу ко всем узлам. При таком подходе структура управления может быть «плоской», с одним «мастер» узлом и n-1 «подчинёнными» исполнителями. Для такой структуры количество решений будет равно n.

Отсутствие маршрута между какими-либо узлами, когда для некоторых i и j значение L ij = NA , будет уменьшать количество возможных вариантов построения иерархии. При некотором раскладе характеристик при невозможности подключить к дереву какой либо j узел, для которого все L ij = NA решений задачи не будет, т.е. рано 0.

Таким образом, для случайно выбранных и распределённых величин С_; и L ij количество решений для n исполнителей может находиться в пределах от 0 до n!

Оптимизатор

В результате экспериментов с описанными выше переменными и ограничениями был подобран подход с двух-шаговой оптимизацией. При первом проходе оптимизации использовалась целевая функция и несколько эвристик: жадность, первоочередное подключение к дереву самых «коммуникабельных», первоочередное подключение к дереву самых «тяжёлых» исполнителей.

Под «тяжестью» исполнителя подразумевается величина самого короткого возможного пути L m ⁱⁿ = min(L' jj + S , ) до данного исполнителя j . Т.е. логика данной эвристики - пытаться подключать к дереву вначале те узлы, которые будут гарантированно при любом раскладе требовать большего времени, чтобы пропустить через эти узлы информационные сигналы. Данную эвристику можно сравнить с логикой первоначального помещения «больших» объектов в задаче о ранце (Knapsack problem).

Для поиска экстремума целевой функции в первом проходе использовался метод градиентного спуска, где для различных эвристик в целевой функции подбирались и запоминались подходящие весовые к-ты эвристик до тех пор, пока находились новые локальные экстремумы.

Для второго прохода оптимизатора использовался метод перестановок. Два терминальных узла менялись «мастер»- узлами, при этом если максимальная длина цепи T_max в дереве при этом уменьшалась – оптимизированная структура запоминалась и цикл повторялся сначала со всеми терминальными узлами. Для примера 3 при n=100 количество терминальных исполнителей равно 68, что даёт 68! вариантов подключения терминальных узлов к «мастер» узлам.

Пошаговое описание работы оптимизатора

Этап 1. Градиентный спуск

Шаг 1.1. Инициализация

Задаём количество исполнителей n . Формируем наборы случайных или предопределённых величин в матрицах L, S, C .

Запрещаем все маршруты из вершины i в эту же вершину L ii = NA .

Для некоторых i и j маршруты могут случайным образом отсутствовать L ij = NA.

Строим расширенные матрицы L', S', C' с учётом вершины Start. Из вершины Start возможен маршрут до любой другой вершины. Значение коммуникабельности С₀ для вершины Start равно 1. Т.е. построить маршрут из вершины Start до любой другой вершины можем только один раз.

Вычисляем «тяжесть» каждого узла- строим матрицу L m ⁱⁿ (минимально возможное расстояние до каждого узла j , определяемое как L m ⁱⁿ = mln(L‘₁ j + S ^ ) .

Из матрицы L' создаём дата фрейм DF всех возможных маршрутов из i в j, включая вершину Start. Значение L ij = NA означает, что маршрут из вершины i в j невозможен.

Path = numeric(), # суммарная длина ветки от вершины дерева(Start) до узла i Path_next = numeric(),# суммарная длина от вершины дерева до j на следующем ходе C= numeric(),      # коммуникабельность, обратный счётчик

R = numeric()     # номер выбранного маршрута по порядку

)

При первоначальной инициализации поле DF.C заполняется для всех элементов j из матрицы С .

Длина маршрутов DF.Path_ next рассчитывается как сумма DF. Path + L ij + S j .

Шаг 1.2. Инициализация весовых коэффициентов эвристик

Для градиентного поиска задаём случайную первоначальную точку коэффициентов эвристик h1_start (жадность), h2_start (подключать коммуникабельных), h3_start (подключать вначале «тяжёлые» узлы).

Значение T_maxbest принимается изначально как бесконечно большое число и далее будет заменено в случае нахождения нового дерева с меньшим значением T_max .

Шаг 1.3. Цикл градиентного поиска лучших весов коэффициентов эвристик

Изучаем пространство, последовательно пробуем изменять коэффициенты эвристик на небольшую дельту 0.1 в сторону увеличения и в сторону уменьшения, пример кода:

for (h1 in c( h1_start-0.1 , h1_start+0.1 , h1_start)) { for (h2 in c( h2_start-0.1 , h2_start+0.1 , h2_start)) { for (h3 in c( h3_start-0.1 , h3_start+0.1 , h3_start)) { ...

Шаг 1.4. Цикл выбора следующей ветви дерева

Организуем цикл - пока в DF не будут подключены к дереву все узлы j , т.е. не будет заполнено поле DM.R для каждого j :

Шаг 1.5. Вычисление веса каждого потенциального маршрута

Для выбора следующего маршрута i. ^ j для каждой строки DF вычисляем вес W_tj :

Н1 = (max(DF. PathNext) — min(DF. Path))/(DF. PathNext — min(DF. Path)  )

H1 = H1/max(H1)

#нормирование

H2 = DF.C/max(DF. C)

H3 = L ^min /max(L ^min )

Для выбора следующего маршрута вычисляем вес каждого маршрута i ^ j с учётом к-тов эвристик W ij = hl * H1 + h2 * H2 + h3 * H3

Для каждого маршрута i ^ j заполняются поля DF.W.

Шаг 1.6. Выбирается следующий маршрут с максимальным весом

Выбирается маршрут i ^ j с максимальным значением max( DF.W) . Если веса маршрутов равны, происходит случайный выбор одного из маршрутов.

Для выбранного маршрута проставляет следующий по счёту номер выбранного маршрута DF.R . После подключения к дереву всех вершин поле DF.R будет иметь значения от 1 до n-1.

Для всех i после выбора маршрута декрементируется поле DF.C , т.е. ресурс коммуникабельности для выбранного узла i уменьшается на 1. Значение DF.C=0 будет означать, что ресурс коммуникабельности для данного узла выбран полностью.

Если к дереву подключены не все узлы – переход к шагу 1.4.

Шаг 1.7. Оценка T_max дерева

После построения дерева находим T_max = max(DF. PathNext)

В случае, если T_max для построенного дерева меньше, чем запомненное значение T_maxbe , то присваиваем T maxbest = ^ max

Точки h1_start , ^2 start , h3_start обновляются текущим «лучшим» значением к-том эвристик hl , h2 , h3 как оптимальные для заданного набора исполнителей и их характеристик.

Цикл по Шагу 1.3. повторяется.

В случае, если были испытаны все окрестности hl , h2 , h3 и при этом не был найден новый экстремум, то считаем, что оптимальное дерево для заданных n исполнителей было найдено, выходим из цикла градиентного поиска.

Этап 2. Метод перестановок

Шаг 2.1. Находим все терминальные узлы

В дата фрейме DF находим все терминальные узлы j, не имеющие последующих подключённых узлов.

Находим самый «удалённый» терминальный узел, имеющий максимальное значение DF.PathNext, и , соответственно, определяющий T_max всего дерева.

Шаг 2.2. Последовательно пробуем менять у терминальных узлов мастер узлы

Меняем поля DF.i и DF.R для самого «удалённого» и другого терминального узла. Пересчитываем поля DF.PathNext и T_max = max(DF. PathNext) .

В случае, если перестановка уменьшила T_max дерева - запоминаем новые значения в DF переход к шагу 2.1.

В случае, если последовательная попарная перестановка всех терминальных узлов с самым удалённым узлом не дала улучшения T_max - выходим из цикла.

Шаг 2.3. Вывод графического отображения дерева

Приводим дерево из дата-фрейма DF в строковый формат Newick.

Выводим дерево на печать используя библиотеку APE.

Заключение

В работе рассмотрено моделирование организации как иерархической структуры, которую можно оптимизировать, свести к графу и решению NP трудной задачи. При одном и том же наборе исполнителей эффективность организации может различаться кратно.

При моделировании существенно упрощены характеристики исполнителей и их контекстная функциональность. Используемые характеристики исполнителей могут быть применены как для людей, так и для автоматизированных/роботизированных систем, что позволяет анализировать поведение организации при появлении в ней «суперисполнителей», существенно отличающихся от средних характеристик обычного человека.

В результате моделирования оптимальных структур получены результаты - более «сообразительные», «коммуникабельные», «находящееся в центре связей» исполнители занимают более высокие места в иерархии и это положительно сказывается на эффективности организации в целом.

Для более сложных исследований характеристики исполнителей могут детализироваться. Человек, как индивидуум, всегда содержит все четыре функции цикла OODA (observe, orient, decide, act). Для автоматизированных систем эти функции могут выноситься в отдельные подсистемы и могут быть разнесены.

Конкурентная среда будет в ближайшее время вынуждать коммерческие и некоммерческие организации всё более и более активно применять инструменты автоматизации, роботизации, методы оптимизации своих процессов, в том числе более рационального выстраивания иерархии управления. Оцифровка и применение компьютерного решения оптимизации иерархии управления позволяет повысить качество такого решения по сравнению с «ручным» решением данной задачи человеком.