Моделирование и оптимизация технологических систем с распределенными параметрами
Автор: Демиденко Николай Данилович, Кулагина Людмила Владимировна
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 3 (55), 2014 года.
Бесплатный доступ
Рассмотрена задача моделирования и оптимального управления ректификационными установками, состоящими из технологических печей и ректификационных колонн. Такая сложная система исследуется как система с распределенными параметрами, поскольку для описания статических и динамических режимов применяется математический аппарат дифференциальных уравнений в частных производных. Обычно в научной литературе излагаются результаты исследований режимов работы отдельных аппаратов. Исследований установок, содержащих несколько объектов с различными технологическими процессами, значительно меньше в связи со сложным математическим описанием и громоздкими вычислениями. Решений задач по оптимальному управлению такими сложными установками еще меньше. Используя феноменологический подход, построена математическая модель тепловых процессов в технологических печах и процессов разделения многокомпонентных смесей в ректификационных колоннах. Модель содержит уравнения в частных производных для процессов теплообмена, массообмена и гидродинамики течения дымовых газов в технологической печи и уравнения массопередачи в ректификационной колонне. В связи с тем, что процессы происходят с рециркуляцией взаимодействующих потоков, граничные условия процесса массообмена в ректификационных колоннах содержат уравнения с обыкновенными производными. Эти условия заданы на разных концах аппаратов. Для расчета оптимальных режимов установки сформулирована задача оптимального управления качеством целевого продукта и получены необходимые условия оптимальности. Поскольку управляющие функции входят в основные граничные уравнения, вариации управлений в области и на границе не являются независимыми, что отражается на структуре сопряженной задачи. При этом используется аргументация вариационного исчисления. Необходимые условия оптимальности содержат исходную краевую задачу, сопряженную относительно функций Лагранжа. Решение исходной и краевой задач позволяет определить оптимальное управление и параметры технологического процесса. Приведены численные результаты с управляющим потоком сырья в дебутанизаторе установки сернокислотного алкилирования изобутана бутиленами. Для этого разработан численный алгоритм. Особенностью разработанного алгоритма является решение задач с граничными условиями для некоторых параметров на противоположных концах области. Кроме того, функции Лагранжа сопряженной системы заданы в конечный момент времени. Рассчитаны оптимальные показатели массообменного процесса: концентрации целевого продукта в дефлегматоре и в кубе.
Математическое моделирование, системы с распределенными параметрами, оптимальное управление, тепломассообмен
Короткий адрес: https://sciup.org/148177291
IDR: 148177291 | УДК: 62-501.6
Текст научной статьи Моделирование и оптимизация технологических систем с распределенными параметрами
Введение. На нефтеперерабатывающих заводах ведется переработка нефти в бензин, керосин, мазут, смазочные масла, сырье для нефтехимии и т. д. Переработка осуществляется в технологических установках для первичной переработки, каталитического риформинга, каталитического крекинга и т. д. Основными аппаратами установок являются трубчатые печи, ректификационные колонны и др. Основу работы этих аппаратов составляют процессы теплообмена, массообмена и гидродинамики взаимодействующих потоков. Анализ процессов и проектирование эффективных режимов рассматриваемых объектов химической технологии с целью создания автоматизированных систем контроля и управления является важнейшей проблемой современного производства.
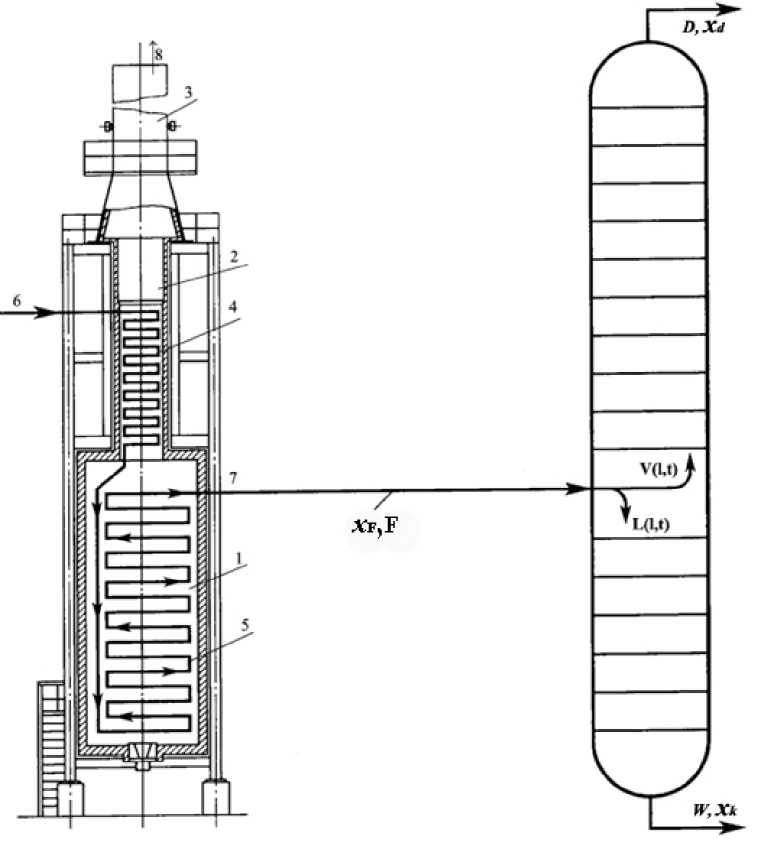
Математические методы и вычислительные средства позволяют осуществить процесс моделирования и оптимизации сложных технологических установок, включающих технологические печи, ректификационные колонны и др. Для описания таких процессов всей установки возможна математическая модель всей цепочки. На рис. 1 приведена принципиальная схема подобной установки. Опыт исследования отдельных аппаратов уже накоплен достаточный, и возможен подход к исследованию установки в целом. В работе исследуемые объекты химической технологии рассматриваются как объекты с распределенными параметрами, для описания которых применяется математический аппарат дифференциальных уравнений в частных производных. Для анализа статических и динамических режимов и решения задач оптимального управления формулируются соответствующие краевые задачи.
Ректификационная установка состоит из технологической печи и ректификационных колонн. Трубчатые печи разных конструкций широко распростране- ны в нефтегазоперерабатывающей, нефтехимической и других отраслях промышленности, являются составной частью многих установок и применяются в различных технологических процессах (перегонка нефти и мазута, пиролиз, каталитический крекинг, очистка масел и др.). В печи сырье нагревается до требуемой температуры и подается в среднюю часть колонны для разделения смеси на компоненты.
Трубчатая печь имеет камеры радиации и конвекции (рис. 1). В камере радиации (топочной камере), где сжигается топливо, размещена радиантная поверхность (экран), поглощающая лучистое тепло в основном за счет радиации. В камере конвекции расположены конвекционные трубы, воспринимающие тепло, главным образом, при соприкосновении дымовых газов с поверхностью нагрева труб конвекции.
Уравнения процессов в технологической печи. При исследовании процесса горения капель жидкого топлива в воздухе в основном представляет интерес распределение концентраций компонентов, плотности, температуры сырья, температуры и скорости ды- мовых газов в печи при статических и динамических режимах работы. Исходя из одномерности движения потока, математическая модель нестационарного горения может быть представлена следующими уравнениями [1]:
-
1. Уравнение неразрывности
dp + 5(рu)=0
д t 61 :
где p - массовая плотность смеси, и - скорость движения смеси.
Для покомпонентной модели процесса горения уравнение (1) можно записать в виде
6 ( p x ) 6 ( p xu ) p x "IT ' Т- ,
где ℓ – линейный размер; х – концентрация горючего
вещества в смеси (0≤ х ≤1); τ – время сгорания.
2. Уравнение движения в виде
ρ
д u
д u
д P
д t
+ u I + —
d t
d t
0,
где P – давление.
3. Уравнение сохранения энергии
f дS д S ) _ px
p Tп I + u^ I— q - Q (Tn) +
V д t tit ) т
+ K 1 ( T c1 - T n ) + K 1 ( T c2 - T n ) , (4)
где q – теплота сгорания топлива; Т П – температура дымовых газов; Q ( T П ) – потери на излучение; T c 1 , T c 2 – температура нагреваемого сырья, движущегося
в нижнем и верхнем направлении; К 1 – коэффициент теплопередачи; S – энтропия, причем
S — C v ln P ( Y — 1 - 1,4 ) .
ρ γ
4. Уравнение теплообмена между нагреваемым сырьем, движущимся в низ и верх печи, и дымовыми газами можно записать в следующем виде:
T- w ^T- — K 2 ( T n - T c ) - Q ( T n ); (5)
aTr + w ^W — K 2 ( T П " T c2 ) - Q ( T n ), (6)
К 2 – коэффициент теплопередачи; w – скорость течения сырья.
Для постановки краевой задачи необходимо задать неизвестные параметры в начальный момент времени и на границе объекта.
a б
Рис. 1. Схема ректификационной установки: а – технологическая печь; б – ректификационная колонна; 1 – камера радиации (топочная камера); 2 – камера конвекции; 3 – дымовая труба; 4 – конвекционные трубы; 5 – радиантные трубы; 6 – вход сырья; 7 – выход сырья; 8 – дымовые газы
Начальные условия:
p( ^ , 0) = P o , x ( / ,0) = x 0 , и ( / ,0) = и 0 , T n ( / , 0) = T n0 , T c 1 ( / , 0 ) = T 0 , T 2 ( / , 0 ) = T c 2 0 .
Граничные условия:
P (0, t ) = a 1 , x (0, t ) = a 2 , и (0, t ) = a 3 ,
T n (0, t ) = a 4 , T c 1 ( L , t ) = a 5 , T c 2 ( 0, t ) = T ^ ( 0, t ) = a 6 ,
где L – длина печи.
На базе системы (1)-(8) можно сформулировать и решить задачи оптимального управления с различными управляющими параметрами [2-6].
Расчет динамических режимов трубчатых печей. Рассмотрим следующую тепломассообменную задачу для процессов в трубчатой печи. Для этого приведем систему (1)–(6) к следующему виду:
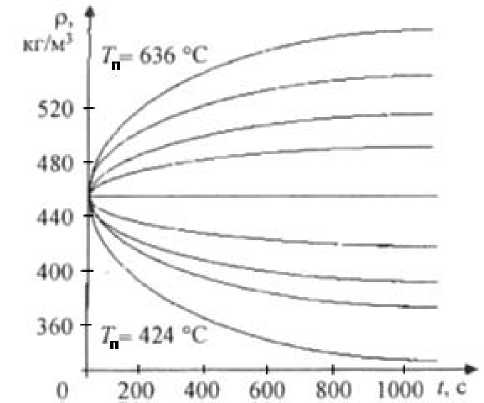
Рис. 2. Кривые разгона по плотности потока в зависимости от температуры потока (от 424 до 636 °С)
д р д р д и
— = — и--р —, дt д/ д/ дx дxx
— = — и, д t д/ д и д и „д
— = — и R —П дt д/
^^^^^^в
RT n д р p д / ’
д T ди д T
П = (1 - Y) T — и П +
П
x
‘ +--q
^^^^^^в
Q ( T n , T c1 , T c2 ) +
С v ρ
+ K 1 ( T — T n ) + K 1 ( T c2 д-ХС—
= w + K 2 T П
— Tn),
— Т —
д t д / 2 V n С 7
— Q ( Т П ) , t € [ 0, T ] , / € [ 0, L ] ,
д T 2 д T 2
—— = — w ——
— Т —
д t
-Q ( т n),
д / 2V n '
t € [ 0, T ] , / € [ 0, L ] ,
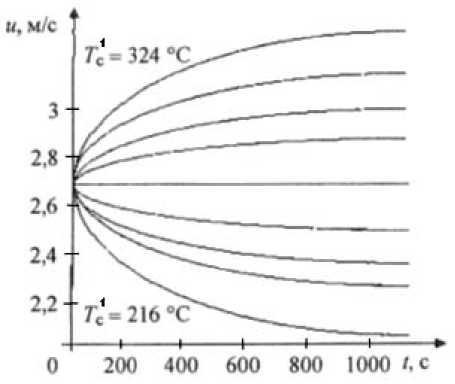
Рис. 3. Кривые разгона по скорости потока дымовых газов в зависимости от температуры сырья (от 216 до 324 °С)
где L 1 – точка вывода сырья из печи. Таким образом, сформулирована краевая задача (7)–(9). Здесь температура сырья T c 1 задается в точке ℓ = L , так как сырье подается сверху в печь, и таким образом мы имеем противоточный технологический процесс.
Кривые разгона на выходе печи получены при возмущении на ± 20 % с шагом 5 % на входе печи по температуре сырья и по температуре дымовых газов (рис. 2–5).
Кривые переходных процессов для плотности, скорости, температуры потока дымовых газов и температуры сырья используются при решении задач локальной автоматики промышленных установок.
Необходимые условия оптимальности в задаче управления объектами с рециркуляцией взаимодействующих потоков. Рассмотрим задачу оптимального управления расходом сырья F в ректификационной колонне.
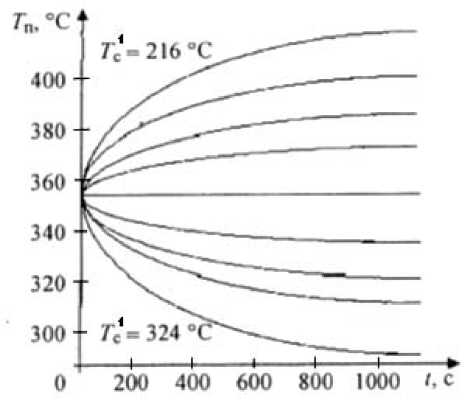
Рис. 4. Кривые разгона по температуре дымовых газов в зависимости от температуры сырья (от 216 до 324 °С)
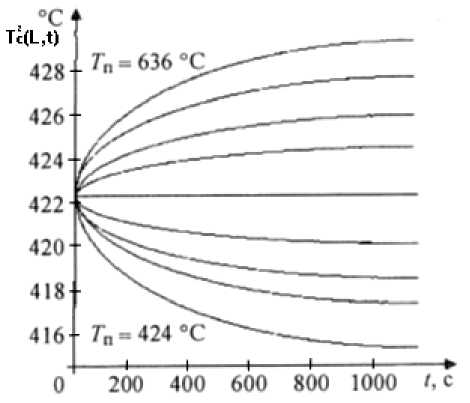
Рис. 5. Кривые разгона по температуре сырья в зависимости от температуры потока газов (от 424 до 636 °С)
Для получения необходимых условий оптимальности (условий стационарности) используются методы классического вариационного исчисления [5-15]. Управления предполагаются кусочно-непрерывными, а соответствующие им решения - непрерывными и кусочно-гладкими.
Здесь рассматривается следующая модель процесса [16]:
д ( Lx ) d t д( Vy ) d t
д( Hxx) — дt dHy) д t
= k ( У - У *( x ) ) + F ( t )Ф x ( t ) x F ,
= k ( y *( x ) - y ) , 0 < t < T , 0 < t < L .
Краевые условия: при I = 0
ности в жидкости и паре; xd - концентрация целевого продукта в дефлегматоре; xk - концентрация целевого продукта в кубе. Возмущающее воздействие по концентрации целевого продукта в сырье F 2 (рис. 6, а ); y * - равновесная концентрация целевого продукта в паровой фазе; D , W - отбор целевого продукта вверху и внизу колонны; Ld - орошение.
Величины потоков при этом удовлетворяют условиям
W ( t ) +D ( t ) = F ( t ), D ( t ) +L d ( t ) = V ( 1, t ) , (14)
W ( t ) + V ( 0, t ) = L (0, t ), V d ( t ) = V ( 1, t ) .
Предполагается, что удерживающие способности Hx , Hy постоянны, V не зависит от I .
Анализ условий (14) показывает, что только два из четырех потоков ( W , D , L , V ) являются независимыми. Выбор тех или иных двух независимых потоков в качестве управлений определяет соответствующие задачи. Эти задачи рассматриваются как задачи оптимального управления в классе кусочно-непрерывных управлений с критерием качества:
tl 2
I = JJ ( y ( t , t ) - 9 * ( t , t ) ) d t d t , (15)
0 0
где 9 * - заданное значение концентрации целевого продукта.
Потоки L , D фиксированы, а V , Vd , Ld исключаются согласно (14). Управление F выбирается в классе кусочно-непрерывных функций и принимает значение в промежутке
F mm< F ( t ) < F max .
Переходя к нормальной форме дифференциальных уравнений (10)-(12), получаем следующую задачу. Рассматривается процесс ректификации, описываемый уравнениями d (Hxkxk ) dt
= L ( 0, t ) x ( 0, t ) - V ( 0, t ) y ( 0, t ) - Wxk ( t ) , (11)
:; = Н ^ ( L + L ) Z”
*
+ д7 x + k ( y - y *) +
y (0,t) = a [yk (xk)-xk (t)] + xk (t), при1 = L d^Hddxd) = Vd (t)yd (t)-(Ld (t) + D(t))xd (t), Vdyd (t)- V(L, t) y (L, t) = Ldxd (t)- L(L, t) x(L, t), (12) yd ( ' ) = y (L, ' )+Ed [ yd (xd)- x (L, ' )].
Начальные условия:
x ( t ,0 ) = x 0 ( t ) , y ( t ,0 ) = y 0 ( t ) , 0 < t < 1, x d ( 0 ) = x d 0 , x k ( 0 ) = x k 0 , 0 - a , E d - 1.
Здесь величина F ( t ) - поток сырья в жидкой фазе, подводимый в колонну и являющийся управлением; x ( L , t ) , y ( L , t ) - концентрации целевого продукта в жидкой и паровой фазах; L ( l,t ) - поток жидкости, V ( I , Н) - поток пара; Нх , Hy - удерживающие способ
+ FxF Ф x ]- X, x' i = Z(1), yt = 7Г[-(D + L)Z(2)+ k(y* -y)]s Y, Hy y' i = Z(2)
при краевых условиях x’kt = FT [(L+F)x-Vy-W^k ]= Xk,
Hxk y=a [ yk - xk 1+xk, t = 0, 0 L ] (17) xdt=—[(D+L) yd -(L+D) xd ]-Xd, t =L, 0 (D+L)(yd - y)- L (xd -x )= 0, yd - y - Ed (yd - y )= 0, при начальных условиях (13) и ограничениях на управления (F - Fmin )(Fmax - F )-U 2 = 0, (18) где и - вспомогательное управление. Задача состоит в том, чтобы в множестве кусочнонепрерывных функций F, удовлетворяющих условию (18), найти такую, что соответствующее ей решение задачи (16)-(18), (13) дает минимум интегралу (15). Применяя известную процедуру вариационного исчисления, получаем необходимое условие оптималь ности: ' L + L x ' ( ^t = k (У ) - ξ ^^^^^^в η H , ' V П t+— nt = k Hy (^ H к - x ^^^^^^в η H 3) далее полагаем Fn+1) = Fn) - aH; 4) предельные значения F(n+1) при n ^ да дают оптимальные управления. На рис. 6 приведены результаты расчетов по оптимальному управлению для промышленной колонны К-34 [17-20] установки сернокислотного алкилирования изобутана бутиленами (разделяемая многокомпонентная смесь сведена к бинарной). Основные параметры: D = 27,06 кмоль/ч, W = 76,59 кмоль/ч, Ld = 45,21 кмоль/ч, Hxd = 50 кмоль, Hxk = 30 кмоль. при I = 0, 0 < t< T dZ^= Z W dt HXk <> (L + F)-^(L + L) = 0, V Л_ — — Z (2)= 0; h„ h. k xk J при t = T, 0 < I< L, ^ = 0, n = 0; при I = L, 0 < t< T ^ = L+D Z k- LZ d2), Z «( T ) = 0, d t - — Z ^1-+ Z (2)V + Z £- = 0, dd d Hxd (,' z(2)—^ L —^ L - z(3)Ed y* d d d d j ' к Hxd J Hxd ( -0--Z(2)V-Z(3)(1 -Ed) = 0; H d d у d J - при 0 < t< T 0,20 \- а б в г Рис. 6. Графики изменения концентрации бутана в сырье (а), дефлегматоре (б) и кубе (в) при управлении потоком сырья (г) * H = [-^Lx + Ф xF h dtdf х F 0 x \ ^^^^^^B * dLz(1-dF dt ^^^^^^B Z(1) - "FT ( xk - x ) +Y (F™ + Fmax - 2F ) = 0, H Yu = 0, где ^, n, Z(1)d, Z(2)d, Z(3)d, Z(1)k, Z(2)k - множители Лагранжа. Алгоритм решения задачи оптимального управления содержит следующие этапы: 1) задается начальное приближение управляющей функции F°( t); 2) решается система уравнений (10)-(13) и (19)(21); Заключение. Приведенная математическая модель процесса горения в технологических печах и процессов разделения в ректификационных колоннах является основной для проектирования оптимальных режимов промышленных установок. Расчет статических и динамических характеристик управляемого процесса позволяет определить основные параметры оптимальных процессов управления. Без знания динамических характеристик невозможно управление технологическими процессами в реальных условиях. Возможность получения параметров нестационарных режимов позволяет в режиме реального времени с высокой степенью эффективности избавиться от вредного влияния возмущений. Эффективность данного подхода проиллюстрирована на процессах тепломассообмена в промышленных объектах.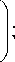
Список литературы Моделирование и оптимизация технологических систем с распределенными параметрами
- Демиденко Н.Д. Моделирование статических и динамических режимов в трубчатых печах//Управление, вычислительная техника и информатика: Вестн. Томского гос. ун-та. 2012. № 3(20). С. 13-21.
- Демиденко Н.Д., Кулагин В.А., Шокин Ю.И. Моделирование и вычислительные технологии распределенных систем. Новосибирск: Наука. 2012. 424 с.
- Демиденко Н.Д. Оптимальное управление режимами технологических печей//Вестник СибГАУ. 2013. № 3 (49). С. 182-187.
- Демиденко Н.Д., Кулагина Л.В. Численный метод исследования стационарных режимов в технологических печах//Engineering & Technologies: J of Siberian Federal University. 2014. 1(7). 55-61.
- Демиденко Н.Д., Кулагина Л.В., Мельник И.Н. Анализ нестационарных режимов в системах контроля и управления распределенными параметрами//Информатика и системы управления: межвуз. сб. науч. тр. Вып. 9. Красноярск: ГУ НИИ информатики и процессов управления. 2004. С. 135-144.
- Демиденко Н.Д., Кулагина Л.В. Оптимальное управление режимами работы технологических печей в нефтеперерабатывающей промышленности//Фундаментальные исследования. 2005. № 2. С. 43-44.
- Демиденко Н.Д. Моделирование и оптимизация тепломассообменных процессов в химической технологии. М.: Наука. 1991. 240 с.
- Демиденко Н.Д., Кулагина Л.В. Методы и средства оптимального управления теплотехнологическими процессами в трубчатых печах//Химическое и нефтегазовое Машиностроение. 2006. № 3. С. 8-9.
- Демиденко Н.Д., Потапов В.И., Шокин Ю.И. Моделирование и оптимизация систем с распределенными параметрами. Новосибирск: Наука, 2006. 551 с.
- Дьяконов С.Г., Елизаров В.И., Лаптев А.Г. Математические основы и моделирование процессов разделения веществ. Казань: Изд-во Казан. ун-та, 1993. 437 с.
- Шахтахтинский Т.Н., Келбалиев Г.И. Аналогия и подобие нестационарных процессов конвективного тепломассопереноса//Докл. РАН. 1990. Т. 315, № 6. С. 1427-1429
- Кафаров В.В., Громов В.Ю., Матвейкин В.Г. Задачи управления объектами химической технологии при наличии нечеткости//Докл. РАН. 1994. Т. 337, № 5. С. 628-630
- Кафаров В.В., Громов В.Ю., Матвейкин В.Г. Математическое моделирование не полностью наблюдаемых химико-технологических объектов//Докл. РАН. 1994. Т. 337, № 1. С. 68-69
- Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. М.: Физматлит, 2001. 320 с.
- Дворецкий С.И., Егоров А.Ф., Дворецкий Д.С. Компьютерное моделирование и оптимизация технологических процессов и оборудования: учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2003. 224 с.
- Демиденко Н.Д., Кулагина Л.В. Особенности сжигания топлива в технологических установках//Химическая техника. 2006. № 7. С. 35-37.
- Кулагина Л.В. Проблема ингерентности и ликвидности перспективных энергогенерирующих систем//Социальные проблемы инженерной экологии, природопользования и ресурсосбережения: Материалы Всерос. науч.-практ. конф. Вып. IX. Красноярск: Краевое НТО, 2003. С. 45-56.
- Демиденко Н.Д. Управляемые распределенные системы. Новосибирск: Наука. 1999. 392 с.
- Демиденко Н.Д., Кулагина Л.В. Повышение эффективности и экологической безопасности сжигания топлива в технологических установках//Энергоэффективность систем жизнеобеспечения города: Материалы VI Всерос. НПК. Красноярск: ИПЦ КГТУ. 2005. С. 276-281.
- Кулагина Л.В. Анализ теплофизических и гидродинамических процессов при сжигании различных видов топлив в энергетическом котле КВ-ТМ-180-150-25//Социальные проблемы инженерной экологии, природопользования и ресурсосбережения: Материалы Всерос. НПК. Вып. X. Красноярск: Краевое НТО. 2004. С. 29-45.


