Моделирование и прогнозирование численности Daphniidae в р. Самаре в 2007 году

Изучена сезонная динамика численности популяций планктонных ветвистоусых ракообразных р. Самары в районе Южного моста в 2007 г. Были построены стохасти

ческие модели для моделировани для прогнозирования наилучшей

В 2007 г. в р. Самаре в черте г. Самары в районе Южного моста выявлено более 20 видов веслоногих и вствистоусых ракообразных, большинство из которых эвритопны. Эти виды относятся к восьми семействам ракообразных: Cyclopoidae, Eudiaptomidae, Bosminidae, Chydoridae, Daphniidae, Sididae, Leptodoridae и Polyphemidae. Нами были проанализированы данные по численности ракообразных, относящихся к семейству Daphniidae, поскольку они доминируют среди других ветвистоусых. Выбор дафнид как объекта для прогнозирования был также определен их практическим значением. Чис- и прогнозирования численности дафний, при этом из выбранных оказалась модель AR(2).

ленность дафнид является одним из важнейших критериев оценки состояния экосистем водоемов. Разумеется, подобные модели возможны и для других ракообразных. Полученные результаты были обработаны с помощью программы R — среды анализа наборов статистических данных.

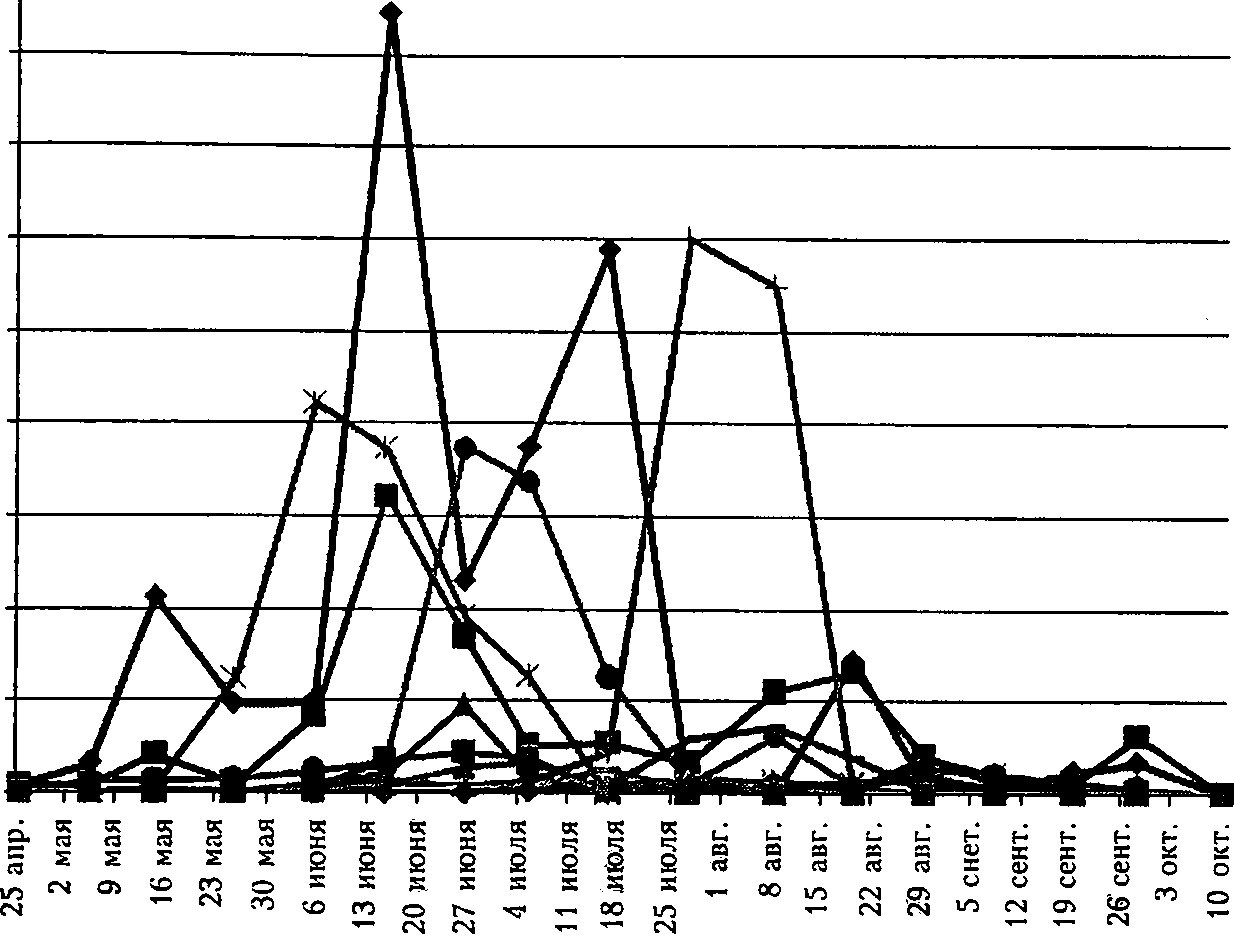
Сезонная динамика плотности популяции веслоногих и ветвистоусых ракообразных и их молоди (j) в экз./л изображена на рис. 1 и 2. Даты замеров (их было 17) и соответствующая численность взрослых дафнид приведены в табл. 1.

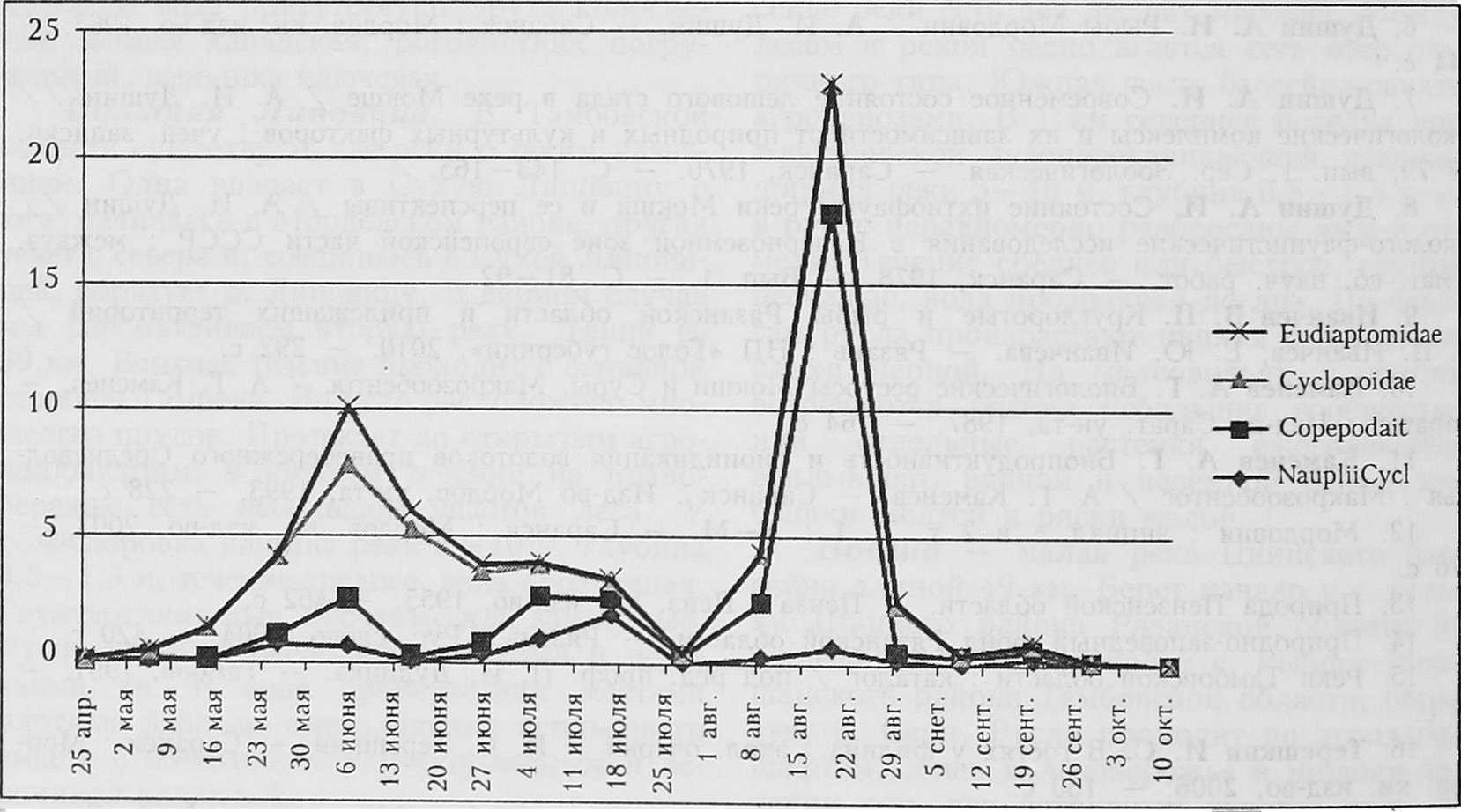
Рис. 1

Сезонная динамика плотности популяции веслоногих ракообразных, экз./л

4,5

—♦— Bosminidae-j

-■1 Bosminidae

—A— Chydoridae-j

X Chydoridae

-Ж..... Daphniidae-j

—♦— Daphhiidae

—H— Sididae-j

— Sididae

~— Leptodoridae-j

♦ Leptodoridae

-W"" Polyphemidae-j

—A..... Polyphemidae

Табл. 1

	27 июля	8 авг.	19 авг.	29 авг.	8 сент.	19 сент.	28 сент.	10 окт.
Daphniidae	0,05	0,31	0,04	0,14	0,1	0,06	0,03	0

Рис. 2

Сезонная динамика плотности популяции ветвистоусых ракообразных и их молоди (j), экз./л

	25 апр.	5 мая	14 мая	25 мая	5 июня	15 июня	26 июня	5 июля	16 июля
Daphniidae	0	0,06	0,07	0,08	0,12	0,17	1,87	1,69	0,63

Типичный для водоемов средней полосы России майско-июньский подъем численности выражен у дафний, особенно у молоди, как результат активного размножения в условиях достаточного количества пищи [1]. Последующее быстрое снижение численности с июле вызвано уменьшением количества съедобных для дафнид диатомовых и зеленых водорослей, а также увеличением по мере прогрева воды численности теплолюбивых сине-зеленых водорослей, малодоступных для питания ракообразных. Определенную роль играет и выедание дафний хищниками [3; 5].

Размножение и вымирание дафний относится к процессам, сложным вероятностным образом изменяющихся во времени, по результатам наблюдений за этими процессами. Однако возможно описание и предсказание численности дафний при помощи стохастической модели: подобные модели построены для речных потоков, динамики ряда биологических популяций, солнечных пятен и др.

Это вызвано случайным характером этих процессов и определяло особенности описывающих их систем. Традиционно системы рассматриваются как детерминированные или стохастические. Принципиальным недостатком детерминированных моделей систем является отсутствие эффективного метода сравнения различных возможных моделей, создаваемых на основе одних и тех же эмпирических данных. Кроме того, детерминированная модель крайне неэффективна при наличии сильно нерегулярных флуктуации или в тех случаях, когда она основывается па неправильной или неполной форме: игнорируется вероятностный характер данных.

Случайных факторов, влияющих на чис-j ленность дафний, настолько много, что неце-| лссообразио рассматривать детерминированные модели. Следует отметить модели авторегрессии (AR), которые оказались удачными в случае моделирования численности : дафний. Это важный класс стохастических динамических моделей, а в вычислительном отношении это еще и простейший класс.

Авторегрессионная ^АЮ модель — 1 модель временных рядов, в которой значения : временного ряда в данный момент линейно | зависят от предыдущих значений этого же ряда. Авторегрессионный процесс порядка р | (AR(p)-процесс) определяется следующим J образом:

г/(^) = с+ 2 a_tyU - г) + w(t\

| z где av ..., dp — параметры модели (коэффициенты авторегрессии), с — постоянная (ча-| сто для упрощения предполагается равной нулю), \w($ — белый шум, т. е. последовательность независимых и одинаково распре-деленных случайных величин (как правило, нормальных), с нулевым средним.

Простейшим примером является авторегрессионный процесс первого порядка — AR(1/процесс:

i          у(0 = с + ry^t -1) + wUY

Для данного процесса коэффициент авторегрессии совпадает с коэффициентом ав-I токорреляции первого порядка.

Другой простой процесс — процесс Юла — АП(2)-процесс:

z/to = с + a_xy^t - 1) + a₂y(t - 2) + w(tY

AR-процесс второго порядка с соответствующими коэффициентами должен иметь коррелограмму типа затухающей синусоиды. Таким образом, AR-процесс второго порядка может представлять эмпирические временные ряды с приблизительно циклическим поведением [2, с. 62].

Мы провели анализ численности популя-I ции дафний подобно тому, как это проводилось для американского журавля [4; 2]. Но эксперименты проводились примерно раз в ; десять дней, что вызвано спецификой вида: их жизненные циклы существенно меньше, чем у журавля. Тем не менее стохастические модели в целом напоминают таковые для журавля, но для учета затухания численности дафний в октябре (и возрождения в апреле) вводится множитель ^(г-э)2- , гдс £) = ^/5. Выбор множителя со значением D = 1/5 служит улучшению авторегрессионной модели и обусловлен общими особенностями гра- фиков численности дафний, в частности, данными за прошлые годы. Таким образом, исследовалась величина

• _У(0 = _Уо(Пе^в<¹-⁹^

где y₀(t) — численность Daphniidae. При этом t — номер эксперимента. Он изменяется от 1 до 17, поэтому t - 9 изменяется от -8 до 8. При этом множитель e^D^^t-^ ^,3 убывает от 25,487097 до единицы и затем снова возрастает до 25,487097. Предположения относительно w(t) давали возможность применить метод наименьших квадратов (МНК).

Для практического применения разработанных моделей было необходимо использование автоматизированных средств анализа, моделирования и прогнозирования. Была использована статистическая программа R, с помощью которой осуществлялась параметризация предложенных моделей и оценка их точности.

R — мощный функциональный язык программирования и среда анализа наборов статистических данных. Будучи средой анализа, R позволяет создавать различные графические представления данных из командной строки. Мы рассмотрели четыре класса моделей: С-, г = 0, 1, 2, 3. Соответствующие уравнения приведены ниже. Пусть у. = V In y(t) = = ln#(O -in^U -1), y₂ = In y{t).

Тогда

£q : z/to = w(t) + 0_O + Q_xy - 1),

Ц : y_x(t) = w(f) +,6₀ + Q_xy_x(t - 1),

£2 ‘ #to = wto + 0_O + 0₁ yU - 1) + 0₂z/(^ - 2), £3 : z/₂(O = _w(t) 4- 0_O + 0^₂ ti -1) 4- 6₂y₂ (t - 2).

Уравнение L_x есть модель типа IAR, оказавшаяся очень успешной при моделировании численности населения США в 1954— 1984 гг. и в исследованиях популяции американского журавля [2, с. 343, 346]. Уравнение L_q — обычный авторегрессионный процесс первого порядка — использовалось в ранних исследованиях популяции американского журавля [4]. Уравнение L₂ — обычный авторегрессионный процесс второго порядка. Уравнение £₃ есть обобщение на стохастический случай модели Гомпертца.

Для оценки параметров различных уравнений мы использовали наблюдения за период с 25 апреля по 19 августа. Наиболее успешным (в первую очередь с учетом коэффициента детерминации) оказались уравнения L₂ и £₃. Соответствующие модели M_i} где г = 2, 3, задаются уравнениями

М₂ : yV) = гу(О + 0,1762 4- 0,7118z/(t -1) -- 0,2803z/(t-2),

М₃ : у-АЙ = w(t) - 0,3621 + 0,4336z/₂U -1) + 4- 0,1594y₂(t - 2).

При этом прогнозировалась численность взрослых особей лишь примерно на 10 дней (на дату следующего замера), в дальнейшем модель уточнялась с учетом нового замера. Иными словами, значения коэффициентов изменялись. Это вызвано большой нестабильностью численности рачков по сравнению с позвоночными, объективной невозможностью точного предсказания на длительный срок.

Подстановка полученных оценок параметров в рассмотренные модели позволила рассчитать сглаженные модельные значения уровней временного ряда y(t). Вывод в пользу той или иной модели временного ряда можно делать по большему значению меры точности моделирования — коэффициенту детерминации. Как известно, коэффициент детерминации (R2) — это квадрат множественного коэффициента корреляции. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных, и вычисляется по формуле где у{ — выборочные данные, у — их среднее значение, fi — соответствующие им значения модели.

Коэффициент принимает значения из интервала [0; 1]. Чем ближе значение к 1, тем ближе модель к эмпирическим наблюдениям. При несущественном статистическом различии коэффициентов детерминации для рассматриваемых моделей предпочтительнее выбрать более простой.

При этом авторегрессионная (и более простая) модель М₂ лучше описывает численность дафний, чем логарифмическая модель М₃. В данном случае для модели М₂ коэффициент R² меняется от 0,3683 до 0,3364, а для модели М₃ коэффициент R² меняется от 0,1975 до 0,1426. Иными словами, в первом случае сила связи умеренная, во втором — слабая. Более сложная модель здесь » обладает худшими предсказательными свойствами и меньшим коэффициентом детерми- | нации, что неудивительно. Известно, что моде- 5 ли, лежащие за пределами определенного \ уровня сложности, часто оказываются более \ низкими по качеству, чем некоторые более простые. Данные прогноза численности дафний по модели М₂ приведены в табл. 2.

Табл. 2

	29 авг.	8 сент.	19 сент.	28 сент.	10 окт.
Daphniidae	0,14	0,10	0,06	0,03	0
Прогноз Daphniidae по модели Л/^	0,06639	0,13217	0,06788	0,03417	0,01434

Учитывая размах колебаний численности дафний в течение весны —осени, можно оценить точность предсказания как хорошую. Дальнейшее обнуление численности в октябре можно предсказать, исходя из общих сезонных условий. Данные прогноза численности дафний по модели М3 приведены в табл. 3.

Табл. 3

	29 авг.	8 сент.	19 сент.	28 сент.	10 окт.
Daphniidae	0,14	0,1	0,06	0,03	0
Прогноз Daphniidae по модели Ж	0,09256	0,09178	0,06804	0,03282	0,01308

Результаты пости дафний

моделирования   числен-  ной численностью представлены на

в сравнении с  рсаль-  рис. 3.

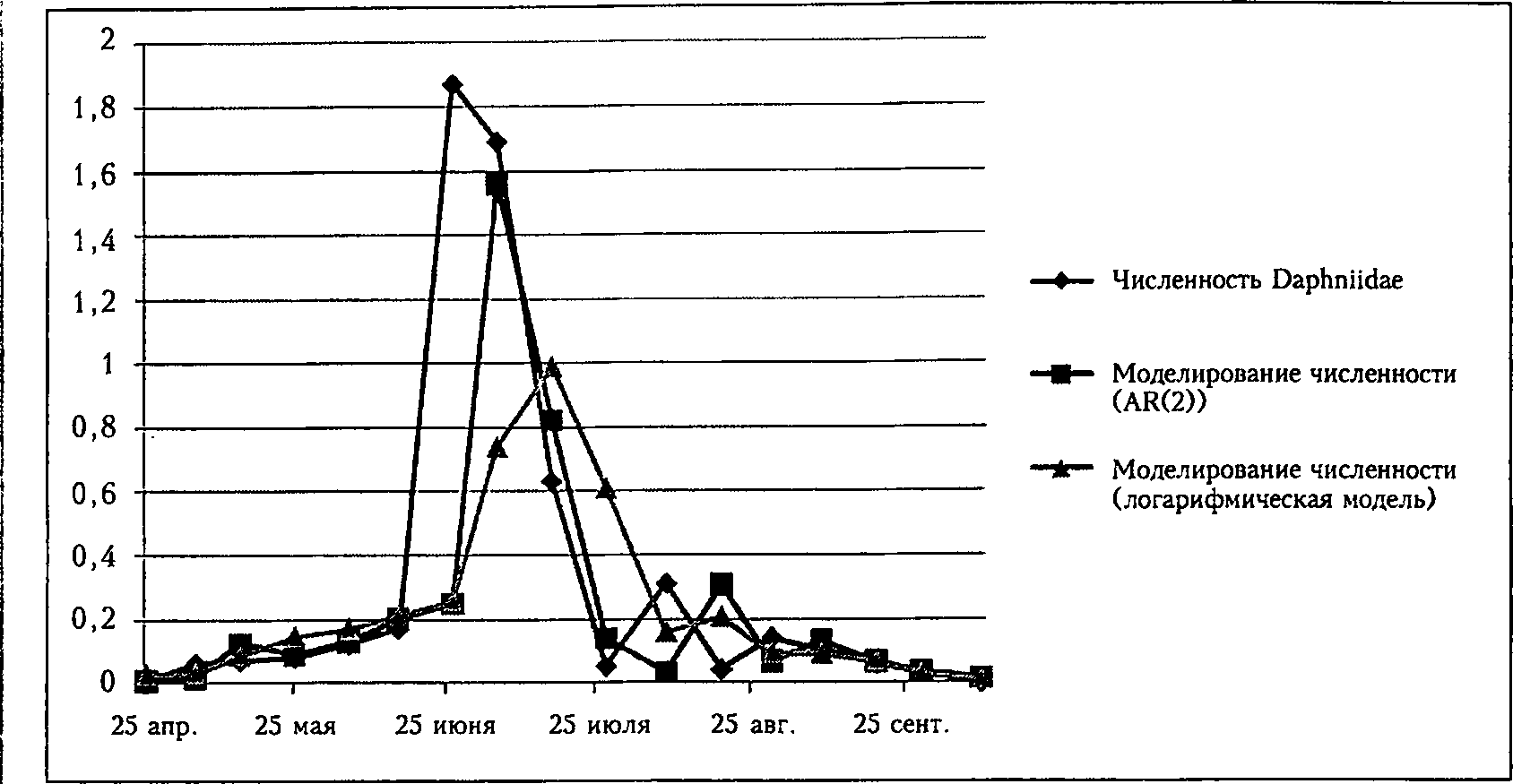
Рис. 3. Сезонная динамика плотности популяции дафний и их моделирование при помощи авторегрессионной и логарифмической моделей, экз./л