Моделирование и прогнозирование курса акций ПАО "Сбербанк"

Разработка методов и алгоритмов прогнозирования капитализации компании является актуальным для оценки её финансовой устойчивости. В качестве таких алгоритмов часто используются модели временных рядов.

В рамках данной работы с целью краткосрочного прогноза произведено построение ARIMA-модели, характеризующей изменение курса акций ПАО «Сбербанк». В качестве исходного ряда Yt взяты 84 значения котировок с 11 сентября 2017 года по 10 января 2018 года. Все расчеты проделаны в статистическом пакете EViews.

На графике временного ряда Y_t , представленном на рисунке 1(а), наблюдается явно выраженная тенденция к росту его уровней. Более того, уместно считать, что математическое ожидание не является постоянным: используя критерий Фишера, основанный на анализе дисперсий, можно отклонить гипотезу о равенстве значений Y [ _1,20 ] и Y [ _65,84 ] выборочного среднего с нулевой вероятностью ошибки. Помимо этого, согласно тесту Дики-Фулера, вероятность ошибки при отклонении гипотезы H₀: a = 1 в уравнении

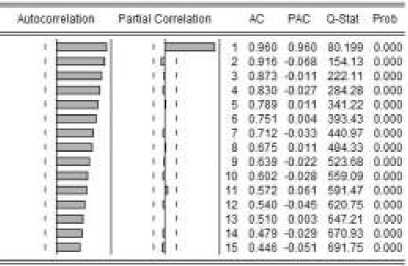
Y t = aY t-1 + ε t , (1) где ε_t – «белый шум», равна 0.9717 > 0.95. Другими словами, имеем все свидетельства нестационарности временного ряда Y_t . Здесь отметим, что исследуемый ряд наилучшим образом описывается именно уравнением (1), то есть моделью авторегрессии первого порядка: в соответствии с коррелограммой на рисунке 1(б) после лага 1 значения коэффициентов автокорреляции постепенно убывают, а коэффициенты частной автокорреляции «обрываются» (становятся незначимыми), что характерно для AR(1). Также обратим внимание на рисунок 2, на котором представлены результаты проведения тестов Фишера и Дики-Фулера.

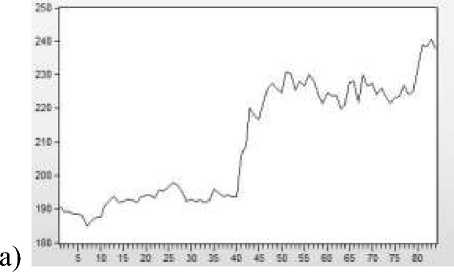
Рисунок 1 – График (а) и коррелограмма (б) временного ряда Yt

б)

Method              df Value Probability                                  t-Statistic Prob*

AnovaF-test (1,38)    666.9997      0.0000 Dickey-Fuller test statistic 1.586671    0.9717

Рисунок 2 – Тесты Фишера и Дики-Фулера

Пусть T(t) – детерминированный тренд нестационарного временного ряда Yt, а εt – его случайная составляющая. Покажем, что T(t) целесообразно аппроксимировать полиномом третьей степени.

Действительно, при построении квадратичной полиномиальной модели установлено, что коэффициент при второй (старшей) степени является статистически не значимым по t-критерию Стьюдента: вероятность ошибки при отклонении гипотезы о равенстве данного коэффициента нулю равна 0.9938 > 0.95. Аналогичным образом аргументируется целесообразность исключения линейного слагаемого из кубической модели (0.0566 > 0.05). В свою очередь, показатели линейной полиномиальной модели уступают характеристикам исправленной кубической модели (в частности, для коэффициентов детерминации имеет место R ² _лин ≈ 0.834224 < R ² _куб ≈ 0.861314 ). Рассмотрение степеней, больших 3, производить не будем, так как увеличение степени приведет к тому, что аппроксимирующий полином станет отражать случайные отклонения, характеризуемые ε_t, а не T(t). Результаты же построения вышеупомянутых моделей можно наблюдать на рисунке 3.

а)

Variable	Coefficient	Std. Error	t-Statistic	Prob.	Variable        Coefficient	Std Error	t-Statistic	Prob.
					C            181.9766	2.405813	75.64036	0.0000
C	181.9907	1 570262	115.8983	0.0000	T            0.652888	0.130634	4.997836	0.0000
T	0.651903	0.032092	20.31365	0.0000	P2          -1.16E-05	0.001489	-0.007784	0.9938
R-squared		0.834224		б)	R-squared	0.834224
Variable	Coefficient	Std Error	t-Statistic	Prob
					Variable        Coefficient	Std. Error	t-Statistic	Prob.
c	190.9492	2.9476 94	64.77920	0.0000		—
T	-0.577582	0.298554	-1.934599	0.0566	C           185.9534	1.445263	128.6641	0.0000
Тл2	0.035965	0.008136	4.420710	0.0000	TA2           0.020706	0.002026	10.21785	0.0000
Тл3	-0.000282	6.29E-05	-4.483329	0.0000	TA3           -0.000170	2.52E-05	-6.758642	0.0000
R-squared		0.867512		г)	R-squared              0.861314

в)

Рисунок 3 – Линейная (а), квадратичная (б), кубическая (в) и исправленная кубическая (г) модели

В результате временной ряд Yt, представленный как

Yt = T(t) + £t « c0 + c1t + c2t2 + c3t3 + £t (t = 1,84), может быть приведен к стационарному виду Xt (t = 4,84) взятием трех

последовательных конечных разностей:

Xt = A3Yt = Yt - 3Yt—1 + 3Yt—2 - Yt-з ~ 3с3 + (£t - 3£t-1 + 3£t-2 - £t-3).

Соответственно, получаем ряд Xt, график которого (визуально без наличия явных тенденций) изображен на рисунке 4(а). Также из соотношения (2)

видно, что Xt описывается линейной комбинацией «белых шумов», то есть некоторой моделью скользящего среднего MA(q). Согласно коррелограмме на рисунке 4(б), после лага 2 значения коэффициентов автокорреляции «обрываются» (становятся незначимыми), а коэффициенты частной автокорреляции постепенно убывают, что соответствует MA(2).

а)

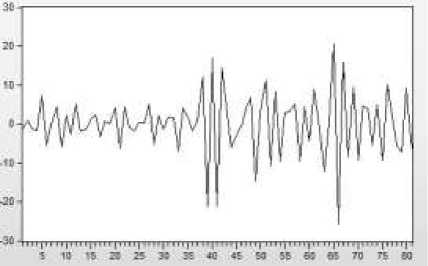
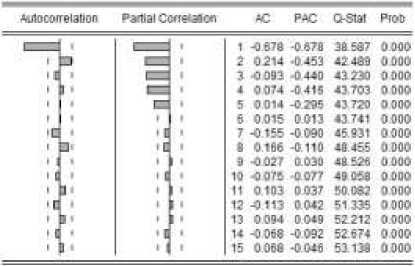
Рисунок 4 - График (а) и коррелограмма (б) временного ряда Xt

На рисунке 5(а) представлен исход моделирования динамики временного ряда Xt процессом скользящего среднего второго порядка. Имеем следующее соотношение:

Xt = et- 1.905279£t-1 + 0.908513et-2. (3)

Заметим, что величина Rma(2) достаточно велика: Rma(2) = 0.825643. Более того, в ходе сравнения построенной модели MA(2) с «близкой» к ней моделью MA(3) установлено, что именно первая наилучшим образом описывает рассматриваемый процесс. В самом деле, согласно рисунку 5(б), в модели MA(3) коэффициент при добавленном регрессоре статистически не значим по t-критерию Стьюдента: вероятность ошибки при отклонении гипотезы о равенстве его нулю равна 0.6321 > 0.05. Помимо этого, ошибка модели MA(2) – «белый шум»: по Q-тесту Люнга-Бокса (для остатков модели), результаты проведения которого можно наблюдать на рисунке 6, вероятность ошибки при отклонении гипотезы об отсутствии автокорреляции до порядка 10 равна 0.531>0.5.

	Variable	Coefficient	Std. Error	t-Statistic	Prob.
	MA(1) MA(2)	-1.905279 0.908513	0.021731 0.020734	-87.67509 43.81753	0.0000 0.0000
а)	R-squared	0.825643

Variable	Coefficient	Std. Error	t-Statistic	Prob.
MA(1)	-1.959468	0.113747	-17.22648	0.0000
MA(2)	1 013603	0.218618	4.636417	0.0000
MA(3)	-0.050990	0.106072	-0.480710	0.6321

б) R-squared             0.826144

Рисунок 5 – Модели скользящего среднего 2-ого (а) и 3-его (б) порядков

Autocorrelation Partial Correlation AC PAC Q-Stat Prob

• •    r| I I I [j I I 10 -0.073 -0.097 6.8697 0.551

Рисунок 6 – Q-тест Люнга-Бокса

Теперь, используя соотношения (2) и (3), перейдем обратно от временного ряда Xt к ряду Yt :

Yt = 3Yt-1 - 3Yt-2 + Yt-3 + εt - 1.905279εt-1 + 0.908513εt-2.

Итак, получили результирующую модель ARIMA(0,3,2), характеризующую динамику ряда Yt , т.е. изменение курса акций ПАО «Сбербанк».

Cравним полученные прогнозные значения (Y₈ ^′ ₅, Y₈ ^′ ₆) на 11 и 12 января 2018 года с известными реальными (Y₈₅ и Y₈₆):

• Y 8′5 = 238.6 ≈ 239 = Y85,|Y8′5 -Y85| ∙ 100% ≈ 0.167%;

• Y 8′6 = 239.4 ≈ 237.75 = Y86,|Y8′6 -Y86| ∙ 100% ≈ 0.694%.

^Y 86

Как видно, прогноз оказался довольно точным: относительные погрешности значительно меньше 1%.