Моделирование и прогнозирование показателей эффективности образовательной деятельности высшего учебного заведения

Одним из показателей национальной безопасности Российской Федерации является уровень обеспеченности ресурсами образования и науки (в процентах от ВВП) [1]. Несомненным является тот факт, что чем больше внимания государство уделяет развитию науки и образования, тем более эффективно работает экономика, растут темпы научно-технического прогресса и, как следствие, увеличивается благосостояние граждан.

Решение проблемы повышения качества образования в вузах России способствует повышению престижа российского высшего образования и его успешной интеграции в международное научно-образовательное пространство. Для оценки качества высшего образования в России используется определение эффективности образовательной деятельности вуза посредством мониторинга. Основная цель мониторинга – формирование информационно-аналитических материалов об образовательных организациях высшего образования с целью контроля их образовательной деятельности.

Мониторинг проводится в несколько этапов.

• 1.    Определение ключевых направлений деятельности образовательных организаций.

• 2.    Выработка показателей их оценки.

• 3.    Сбор и верификация первичных данных статистики.

• 4.    Анализ данных и подготовка предложений:

• 5.    Публикация результатов мониторинга.

• 6.    Использование результатов мониторинга для принятия решений учредителями и при планировании контрольных мероприятий в области образования Федеральной службой по надзору в сфере образования и науки¹.

‒ расчет показателей эффективности деятельности образовательных организаций и их филиалов;

‒ определение пороговых значений на основе медианных значений показателей в рамках референтных групп.

Показатели эффективности вуза рассчитываются на основании «Методики расчета показателей мониторинга эффективности образовательных организаций высшего образования 2017 года»2, в которой определены пороговые значения показателей эффективности деятельности образовательных организаций высшего образования (табл. 1).

Вузы относятся к имеющим признаки неэффективности в том случае, если образовательная организация или ее филиал достигает порогового значения любых 4 из 8 показателей (согласно Приказу Министерства образования и науки РФ от 13.03.2017 г. № 222 «О проведении мониторинга эффективности образовательных организаций высшего образования»).

В 2017 г. Межведомственная комиссия под председательством главы Минобрнауки проанализировала деятельность 769 вузов и 692 филиалов и признала неэффективными 107 вузов и филиалов.

Т а б л и ц а 1

T a b l e 1

Пороговые значения показателей эффективности высших учебных заведений Threshold values of performance indicators of higher education institutions

д р	Показатель эффективности / Performance indicator	Пороговое значение / Threshold value
Х 1	Е.1.1. Образовательная деятельность. Средний балл студентов, принятых по результатам ЕГЭ на обучение по программам очной подготовки бакалавриата и специалитета за счет средств соответствующих бюджетов бюджетной системы РФ и с оплатой стоимости затрат на обучение физическими и юридическими лицами, баллы / Educational activity. The average score of students accepted by the results of the Unified State Examination for full-time education according to the Bachelor’s and Specialization programs at the expense of the corresponding budgets of the budget system of the Russian Federation and with the payment of the cost of training costs by individuals and legal entities, ponts	60,00
Х 2	Е.2.1. Научно-исследовательская деятельность. Объем НИОКР в расчете на одного научно-педагогического работника (НПР), тыс. руб. / Scientific and research activity. The volume of research and development per one scientific and pedagogical worker (SPW), thousand rubles	51,28
Х 3	Е.3.1. Международная деятельность (показатель для вузов). Удельный вес численности иностранных студентов, обучающихся по программам бакалавриата, специалитета, магистратуры, в общей численности студентов (приведенный контингент) / International activity (indicator for universities) . Specific weight of the number of foreign students studying under the Bachelor’s, Specialized, Master’s programs, in the total number of students (estimated contingent)	1,00
Х 4	Е.4.1. Финансово-экономическая деятельность. Доходы образовательной организации из всех источников в расчете на одного НПР, тыс. руб./ Financial and economic activity. Revenues of the educational organization from all sources per SPW, thousand rubles	1 327,57
Х 5	Е.5.1. Заработная плата профессорско-преподавательского состава. Отношение заработной платы профессорско-преподавательского состава к средней заработной плате по экономике региона, % / Salaries of university teachers. The ratio of the salaries of the university teachers to the average wage for the economy of the region, %	150,00
Х 6	Е.6.1. Трудоустройство. Удельный вес выпускников, трудоустроившихся в течение календарного года, следующего за годом выпуска, в общей численности выпускников образовательной организации, обучавшихся по основным образовательным программам высшего образования, % / Employment. Share of graduates who have found employment in the calendar year following the year of release, in the total number of graduates of the educational organization trained in the main educational programs of higher education, %	75,00
Х 7	Е.7.1. Контингент студентов. Приведенный контингент студентов, ед. / Contingent of students. Estimated contingent of students, units	220,00
Х 8	Е.8.7. Дополнительные показатели образовательных организаций. Численность сотрудников, из числа ППС (приведенных к доле ставки), имеющих ученые степени кандидата или доктора наук, в расчете на 100 студентов, ед. / Additional indicators of educational organizations. The number of employees, from the number of teachers (reduced to the share of the rate), having a scientific degree of a candidate or doctor of science, per 100 students	2,78

В связи с этим возникает необхо- системы вуза осуществить имитацион-димость разработки математических ное моделирование и прогнозирование моделей, алгоритмов и программ, по- основных показателей эффективности зволяющих в рамках информационной деятельности вуза, а также разработка Сomputer science, computer engineering and management 123

методики оперативного управления показателями эффективности.

Обзор литературы

Особенности образовательного процесса в высшей школе были проанализированы в трудах К. Арджириса, С. Богомолова, А. Аганбегяна, В. Байденко3, О. Виханского, А. Джуринского, Э. Де-минга4 и др. Учеными исследовались вопросы контроля и управления качеством с учетом основных принципов теории управления и с использованием опыта внедрения передовых методик обучения. В настоящее время в России для получения лицензии на образовательную деятельность вуз должен пройти лицензирование и аккредитацию. Особенности проведения данных процедур описаны в нормативно-правовых документах и трудах исследователей В. Г. Наводнова, Г. Н. Мотовой [2] и др. Однако при проведении процедур лицензирования и аккредитации возникают определенные проблемы, основными среди которых являются периодичность экспертизы и отсутствие учета воздействия различных факторов на качество образовательного процесса на пятилетнем интервале. Вследствие этого показатели аккредитации, рассчитанные на основе одномоментного замера, не предоставляют администрации объективной и точной информации о текущей ситуации в вузе5.

Для описания образовательного процесса также используется большое коли-

Том 28, № 1. 2018

чество показателей, изменение которых требует длительного времени. Подобные проблемы характерны также для процедуры мониторинга эффективности.

Вопросами разработки и использования математических моделей для кон-тролякачестваучебногопроцессазанима-лись такие ученые как О. А. Граничина6, В. П. Сухинин [3], М. В. Горшенина [4], В. И. Мешалкин7. Исследованию проблем разработки математических моделей, алгоритмов и программ посвящены также некоторые работы автора данной статьи [5–6].

Существующий методологический аппарат не предоставляет возможности прогнозирования показателей аккредитации и мониторинга, что, в свою очередь, не позволяет администрации своевременно устранить возникающие негативные тенденции и снижает достоверность проводимой экспертизы. Отсутствие эффективных математических моделей и методов, позволяющих осуществлять аналитическое моделирование и прогнозирование показателей эффективности образовательной деятельности вуза, обусловило актуальность проведенного исследования.

Особенности разработки автоматизированных информационных систем, в т. ч. для образовательных организаций, были проанализированы в трудах как российских (А. М. Бер-шадского8, А. С. Клещева9, Д. А. Новикова [7], О. И. Ларичева [8]), так и зарубежных ученых (I. F. Codd [9], T. R. Gruber10, G. Piatetsky-Shapiro [10], U. Wang11 и др.).

В российских вузах для оценки эффективности их деятельности используются следующие программные решения. Автоматизированная информационная система «Наука» функционирует в ФГБОУ ВО «Самарский государственный технический университет». Она предназначена для анализа результатов и управления научно-исследовательской деятельностью профессорско-преподавательского состава университета.

Кроме этого, для автоматизации процессов в вузах используется «Галактика Управление Вузом»12 – современная информационная система, основными функциями которой являются: осуществление эффективного планирования учебного процесса; объединение основных подразделений в единую информационную систему вуза; снижение трудоемкости процессов обработки данных; обеспечение контроля и управления финансовыми и кадровыми ресурсами и пр. Отметим также информационную систему «Университет», автоматизирующую процессы управления деятельностью высшего учебного заведения и успешно функционирующую в ФГБОУ ВО «Ставропольский государственный университет».

Общими недостатками вышеперечисленных информационных систем являются сложная архитектура, а также слабоструктурированная система экспорта и импорта данных. Ни одна из них не предназначена для вычисления прогнозных значений показателей эффективности образовательной деятельности вуза.

Задачей исследования является разработка математических методов, моделей и программ для моделирования и прогнозирования показателей эффективности деятельности вуза, а также методики оперативного управления показателями эффективности.

Материалы и методы

В разработанный комплекс математических моделей для проведения компьютерных экспериментов по прогнозированию основных показателей эффективности деятельности вуза входят модель системной динамики и регрессионная модель.

В основу метода системной динамики положены следующие допущения:

‒ динамику поведения сложного процесса можно отслеживать с помощью изменения значений «уровней», а сами изменения регулировать «потоками», которые повышают или снижают эти уровни;

‒ все изменения в функционировании системы основаны на «петлях обратных связей», которые являются замкнутыми цепями взаимодействий. Подобная цепь соединяет причину действия с его результатом, изменяющим состояние окружающей среды;

‒ петли обратной связи в системе соединяются нелинейно, поэтому информация об уровнях системы влияет через обратные связи на сами уровни непропорционально и труднопредсказуемо13.

Выберем в качестве моделируемых переменных в разработанной математической модели показатели эффективности деятельности вуза Х ₁– Х ₈, приведенные в табл. 1.

На рис. 1 приведен граф причинноследственных связей между моделируемыми переменными Х1–Х8. Стрелками показаны причинно-следственные связи между переменными, кружками обозначены функциональные зависимости f1(X7), …, f9(X7), определяющие степень влияния одной моделируемой переменной на другую. Причинно-следственные связи для разработанной модели были выбраны путем изучения мнений экспертов, подтвержденных экспериментально при проведении мониторинга в Балаковском филиале ФГБОУ ВО «РАНХиГС».

Проанализируем производные моделируемых переменных Х1–Х8 как функции данных переменных. Производные уровней по времени dXi(t), i = 1...n, ко-dt торые называются потоками, являются скоростями изменения уровней в единицу времени. В этом случае связи между потоками и моделируемыми переменными будут иметь вид систем дифференциальных уравнений:

Для подхода Дж. Форрестера в системной динамике характерны упрощение и декомпозиция системы.

Том 28, № 1. 2018

Представим функции F_i в виде разложений в ряд по степеням X_k ( t ), и проанализируем первые, линейные, члены разложения. Коэффициенты при членах разложения определяются экспериментально. Система в этом случае имеет вид:

dX i ( t )

—"7— = a i,0 + a i,i X 1⁽ t ) + dt

+ ... + a i, _nX_n ( t ), i = 1... n ,          ⁽²⁾

где произведения α_i,k X_k ( t ) , i = 1 …n – темпы i -го потока; t – время.

Поскольку сложная система нелинейна, пусть темпы зависят от уровней: a i , k = a i,k ( X 1 ( t ),... X_n ( t )), k = 1... n . Указанная зависимость имеет мультипликативный вид:

^a i, k ⁽ ^ 1 ⁽ t ),... x n ⁽ t )) =

= ai,kfi,k,1(x1(t))-f,k,n (xn (t)), k = 1... n,                  (3)

где α_i,k – константы из уравнения (2).

Каждый из элементов f_i,k,l,l = 1 ...n мультипликативной модели зависит только от уровня X_l ( t ). За «базовое»

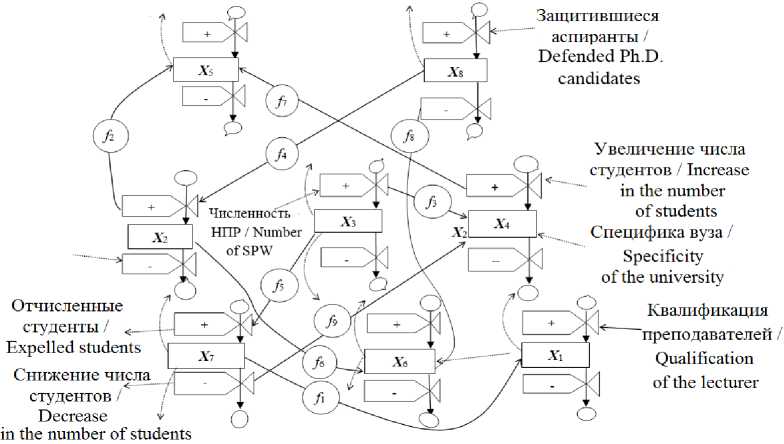
Р и с. 1. Граф причинно-следственных связей между переменными Х ₁– Х ₈

F i g. 1. The graph of cause-effect relations between the variables X ₁– X ₈

126                                   Информатика, вычислительная техника и управление

значение f_i,k,l , от которого под влиянием аргументов они могут отклоняться в ту или иную сторону, принимается 1.

Таким образом, модель имеет вид:

dX i ^ t ) = «, ,о + e « _У гт. / ; ^, . ( x. ( t )), x. ( t ), ;=i-n- (4) dt k = 1 I = 1

Система уравнений (4) дает декомпозицию исходной системы общего вида (1)14.

Проанализируем моделируемую переменную Х ₂ – объем НИОКР в расчете на одного научно-педагогического работника (НПР). Подграф для моделируемой переменной приведен на рис. 2.

Запишем для Х ₂ дифференциальное уравнение следующего вида:

dX ₂( t ) dt

(F (t )• PN (t ))• f,(X8) -(G (t )• PK (t)) (5) ps (t)                 ’ где Х2(t) – текущий объем НИОКР в расчете на одного НПР, руб.; F(t) и G(t) – объем НИОКР в расчете на одного НПР на начало и конец расчетного периода соответственно, руб.; PN(t) и PK(t) – численность НПР на начало и конец расчетного периода, чел.; РS(t) – среднегодовая численность НПР, чел.

Аналогично записываются уравнения для переменных Х ₁ , Х ₃‒ Х ₈.

Таким образом, разработанная на основе системно-динамического подхода математическая модель имеет вид:

dX , ( t ) _ EN ( t ) - EK ( t ) ■ f ( X ₇) dt =          ES ( t )          ^;

dX 2 ( t ) _ F ( t ) ■ PN ( t ) ■ f , ( X ' — G ( t ) ■ PK ( t ) . dt                     PS ( t )                ;

dX ^ _ M ( t ) + Kv ( t ) - S o ( t );

dt dX4(t) _ (SK(t) + Mo(t) + Vr(t) + PN(t))f,(X7)■ f,(X2)

dt

PS ( t )

X ₅( t ) + MTO ( t ) + NR ( t )

PS ( t )           .

dX^^t) _ (US ( t ) + St ( t ) + Gr ( t )) ■ f 2 ( X 2 ) ■ f , ( X ₄) - dt

- ( T ( t ) + 1 ( t ));

dX6^t) _ SV (t) ■ f;(X2) ■ f,(Xs) - (U (t) + SnV (t)); dt dX7-(t) _ Bo (t) + Bz (t) ■ f 5 (Xз) - D (t);

dt dX8 (t) _ EK(t) + KP(t) - (BK(t) + KP(t))

dt ^_               KS ( t )              ’

где Х ₁( t )– X ₈( t ) – текущие значения моделируемых переменных; EN ( t ) и EK ( t ) – средний балл ЕГЭ на начало и конец расчетного периода; ES ( t ) – среднегодовое значение среднего балла ЕГЭ; K_v ( t ) –

Увеличение финансирования Increased funding

Темп уменьшения/ Rate of decrease

Темп увеличения/ ► Rate of increase

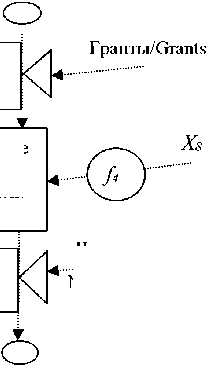
Число студентов

Number of students

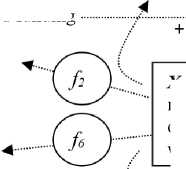
АТ-объем НИОКР в расчете на одного НПР/The volume of research and development work for one SPW

Р и с. 2. Подграф моделируемой переменной Х ₂

F i g. 2. The subgraph of the simulated variable X ₂

ежегодная государственная квота на обучение за рубежом, шт.; S_o ( t ) – стоимость обучения в вузе (руб.); US ( t ) – наличие ученой степени у ППС вуза; St ( t ) – размер ставки ППС в данном учебном году, руб.; G ( t ) – гранты научных фондов, руб.; T ( t ) – налоги, руб.; I ( t ) – уровень инфляции, %; SK ( t ) – средства частных компаний, руб.; Mo ( t ) – средства Минобрнауки, руб.; Vr ( t ) – текущий объем финансирования за расчетный период, руб.; MTO ( t ) – материально-техническая оснащенность учебного процесса, руб.; NR ( t ) – накладные расходы вуза, руб.; SV ( t ) – спрос на бакалавров/ специалистов, чел.; SnV ( t ) – количество выпускников по данному направлению/ специальности, чел.; B ₀( t ) – количество студентов очной формы обучения, чел.; B_z ( t ) – количество студентов заочной формы обучения, чел.; D ( t ) – количество отчисленных студентов на конец учебного года, чел.; BK ( t ) и EK ( t ) – количество кандидатов наук на начало и конец расчетного периода соответственно, чел.; KP ( t ) – количество докторов наук, профессоров, чел.; KS ( t ) – общая численность ППС, чел.

В разработанной математической модели используются следующие функциональные зависимости: f1(X7) – среднего балла студентов от приведенного контингента студентов; f2(X2) – заработной платы ППС от объема НИОКР в расчете на одного НПР; f3(X2) – доходов вуза от объема НИОКР на одного НПР; f4(X8) – объема НИОКР на одного НПР от численности кандидатов/ докторов наук; f5(X3) – приведенного контингента студентов от численности иностранных студентов; f6(X2) – удельного веса трудоустроившихся выпускников от объема НИОКР на одного НПР; f7(X4) – отношения заработной платы ППС от доходов вуза из всех источников на одного НПР; f8(X8) – удельного веса трудоустроившихся выпускников от численности кандидатов/ докторов наук; f9(X7) – приведенного контингента студентов от доходов вуза из всех источников на одного НПР.

Функциональные зависимости f_i ( Х _i ) i = 1…9, определяются экспериментально и могут быть аппроксимированы полиномами 3–4 степени. Например, функциональные зависимости f ₂( X ₂) и f ₃( X ₂) имеют следующий вид:

f , ( X ₂) = 1,2 ■ X ₂ ⁴ - 2,6 ■ X 2 +

• + 1,7 ■ X 2 + 0,63 ■ X ₂ + 0,1;

f 3 ( X ₂) = - 0,52 ■ X 2 + 0,97 ■ X 2 -

• - 0,75 ■ X ₂ ² + 1,2 ■ X ₂ + 0,14.

С целью проверки адекватности математической модели (6) было произведено сравнение расчетных показателей Х ₁– Х ₈ с показателями, полученными по регрессионной модели, а также с ретроспективными данными.

Регрессионная модель была получена с использованием статистических данных (показателей эффективности) в филиале академии на временном интервале 2013–2017 гг. Параметры уравнений регрессии определялись с помощью метода наименьших квадратов. При определении вида регрессионной модели проводился анализ на наличие гетероскедастичности.

X 1 n = - 0,7967 1 ⁴ + 10,035 1 ³ - 44,028 1 ² +

+ 77,11 t + 9,95;

X 2 = 38,288 ■ In | t | - 0,253;

X ₃ ⁿ = - 0,2075 1 ² + 1,2845 1 - 0,6575;

X 44 = 256,1 - In | t | + 1036,7;

X 55 = - 11,569 1 ³ + 102,49 1 ² -

- 24587 1 + 282,18;

X ₆ ⁿ = 5,6501 ■ In | t | + 65,292;

X ₇ ⁿ = - 9,9417 1 ³ + 89,925 1 ² -

- 267,73 t + 683,14;

X ₈ ⁿ = 0,3283 1 ³ - 2,77 1 ² + 6,9817 1 - 1,58.

Проверим адекватность разработанного комплекса моделей. Рассчитаем по модели системной динамики значение переменной Х ₂ в 2016 г. по формуле (5):

X 2 (2016) =

46,97 - 66 - 2,1 - 48,44 - 64

= 52,46 тыс. руб.

Согласно регрессионной модели, Х ₂(2016) = 61 тыс. руб. Фактическое значение переменной Х ₂ в 2016 г. составило 54,43 тыс. руб. Таким образом, абсолютная погрешность вычислений по моделям (6–7) в сравнении с ретроспективными данными варьируется от 4 % до 12 %, что свидетельствует об относительной адекватности комплекса моделей.

Поскольку задача прогнозирования показателей эффективности деятельности вуза является задачей Коши с заданными начальными условиями, то теоретически она может решаться с использованием традиционных численных методов: Эйлера, Рунге-Кутты и др. Однако разработанная математическая модель (6) является сложной, нелинейной, неоднородной, разнотемповой, нестационарной системой дифференциальных уравнений, поэтому использование классического метода Рунге-Кутты 4-го порядка для ее решения вызывает определенные затруднения.

Решить систему (6) можно с помощь «ручного» интегрирования посредством рекуррентной трехшаговой процедуры с интуитивным выбором шага:

• 1)    вычисление временных определенных интегралов от временных функциональных зависимостей;

• 2)    ручной выбор шага для нелинейных функциональных зависимостей по схеме Рунге-Кутты 4-го порядка;

• 3)    подстановка на следующем шаге результатов интегрирования на предыдущем шаге с вычислением временных функциональных зависимостей на текущем шаге.

Результаты исследования

При проведении модельного эксперимента с разработанным математическим обеспечением были рассчитаны показатели эффективности деятельности Балаковского филиала ФГБОУ ВО «РАНХиГС». В качестве начальных значений были выбраны нормированные относительно пороговых показатели эффективности образовательной деятельности вуза за 2017 г.:

X _{0 i} = [0,85; 1,27; 1,19; 1,02; 1,13; 0,93; 1,58; 1,09].

На рис. 3 показаны расчетные показатели по Балаковскому филиалу «РАНХиГС» на интервале [0; 3] года.

При проведении мониторинга эффективности вуза возникает необходимость обработки больших объемов статистических данных, что существенно повышает трудоемкость выполняемых работ. Поэтому для автоматизации вычислений прогнозных значений показателей эффективности требуется разработка специализированного программного обеспечения15 [11–13].

В интегрированной среде разработки ПО Visual Studio на языке программирования C # был создан «Модуль для определения эффективности деятельности высшего учебного заведения»¹⁶. Важным достоинством программы является определение текущей ситуации в вузе и предоставление лицу, принимающему решения, возможности оперативного управления показателями эффективности. Рассмотрим алгоритм работы программы «Модуль для определения эффективности деятельности высшего учебного заведения» [14].

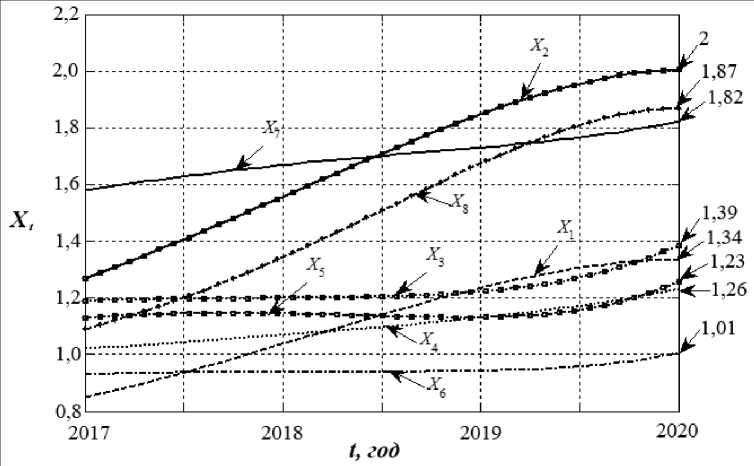
Р и с. 3. Динамика моделируемых переменных Х ₁– Х ₈ на интервале [0; 3] года F i g. 3. Dynamics of the simulated variables X ₁– X ₈ on the interval [0; 3] years

На первом этапе осуществляется выбор местоположения и типа вуза. Значения пороговых показателей мониторинга для различных типов вузов приведены в соответствующих базах данных, созданных в MS Access 2007. Подключения баз к основному блоку программы производится через .NET Framework для OLE DB. После этого вводятся фактические и пороговые значения показателей эффективности, весовые коэффициенты, которые выбираются экспертами. В процессе работы программы вычисляются взвешенные отклонения значений фактических показателей от критических (пороговых). При этом определяется значение целевой функции Z ( t ) по следующей формуле:

j

Z ( t ) =f / - E ( x n ( t ) - X Ф ( t )) • ^ • dt ^ min,

"°' ‘=*                  ^Z                          (8)

где i = 1…j – число показателей эффективности образовательной деятельности; µi – коэффициент (доля) i-го показателя эффективности; Xin – пороговое (критическое) значение показателя эффективности; Xiф – фактическое значение показателя эффективности; 0 < Xiф ≤ 1 – фактические показатели эффективности нормированы; 0 < Xin ≤ 1 – пороговые показатели эффективности подчинены нормальному закону распределения. В качестве начальных условий определим: 0 < X0i ≤ 1. Управляющие воздействия U(t) e u (t) - процедуры решений ЛПР, которые представляют собой линейные уравнения вида: U(t) = at + b; где a, b > 0; t – время.

Целевая функция Z(t) позволяет оперативно управлять образовательной деятельностью вуза посредством варьирования значения показателей и весовых коэффициентов µi. Весовой коэффициент µi служит для гибкого планирования администрацией своей образовательной политики, определяя приоритеты в развитии вуза. С целью достижения необходимой точности и снижения погрешности расчетов определение значений целевой функции (8) необходимо производить 2 спо- собами: 1) численным методом Симпсона; 2) с помощью искусственной нейронной сети Elman backprop. Сеть Элмана характеризуется частичной реккурентностью в виде обратной связи между скрытым и входным слоями нейронов. Данная связь формируется с использованием единичных элементов запаздывания z‒1. Реккурентные сети, по сути своей, являются потомками однонаправленных сетей персептронного типа. Архитектура искусственной нейронной сети Elman backprop представлена на рис. 4.

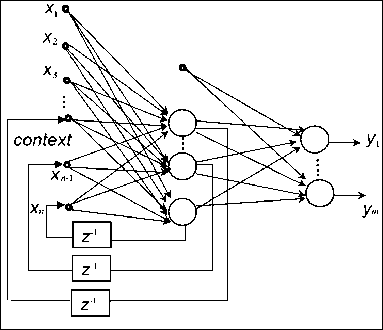
Р и с. 4. Архитектура Elman backprop

F i g. 4. The architecture of Elman backprop

Значения функции Z ( t ) вычислялись по формуле (8), при заданном интервале [ t_нач ; t_кон ], равным соответственно [0; 1] с шагом 0,1 месяца, i = 1…8 – количество показателей эффективности. Определим значения коэффициентов µ_i = const на всех интервалах времени, руководствуясь следующими приоритетами: для Х ₃ – международной деятельности вуза определим µ ₁ = 0,2; для Х ₆ – трудоустройства выпускников µ ₂ = 0,2; для Х ₈ – дополнительные показатели образовательных организаций µ ₂ = 0,2. Значения коэффициентов µ_i приведены в матрице-столбце:

	Ц 1		0,13
	Ц		0,14
	Ц з		0, 20
^ i =	^ 4	=	0,01
	Ц		0,01
	Ц б		0,02
	Ц 7		0,01
	Ц 8		0, 20

Значения функции Z ( t ), рассчитанные по методу Симпсона, приведены в табл. 2.

Т а б л и ц а 2

T a b l e 2

Значения функции Z ( t ), рассчитанные по методу Симпсона

The values of function Z ( t ), calculated by the Simpson method

Z	t
42,5	[0; 0,001]
376,0	[0; 0,1]
654,7	[0; 0,2]
883,3	[0; 0,3]
1066,3	[0; 0,4]
1208,1	[0; 0,5]
1312,7	[0; 0,6]
1384,3	[0; 0,7]
1426,5	[0; 0,8]
1443,0	[0; 0,9]
1437,3	[0; 10]

При создании и обучении нейронной сети обучающее множество было достаточно представительным и включало 15 значений целевой функции Z на заданном интервале. Нейронная сеть обучалась с заданным числом итераций – 1 000. Результаты обучения выводились через 25 итераций при погрешности расчетов 0. Сеть обучилась относительно быстро, пройдя 12 итераций:

[42,6448; 377,9812; 644,8256; 883,6781;

1066,3; 1195,3851; 1313.4688; 1385,3674;

1443,0096; 1443,0167; 1443,0099]

График расчета погрешности при обучении и вид тестовой кривой ней- ронной сети представлены на рис. 5–6 соответственно.

Погрешность вычисления Z(t) по методу Симпсона и с помощью искусственной нейронной сети составляет

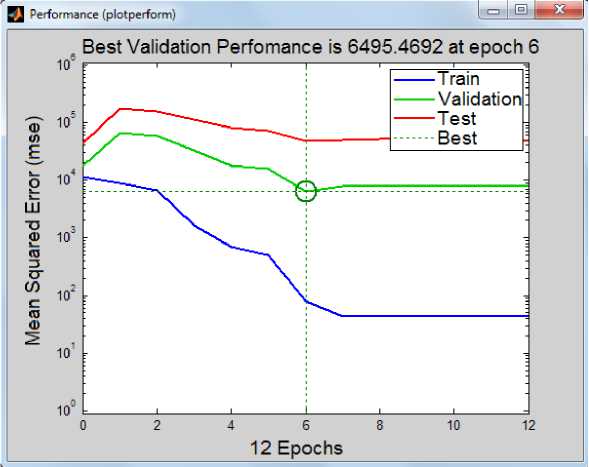
Р и с. 5. Расчет погрешности

F i g. 5. Calculation of error

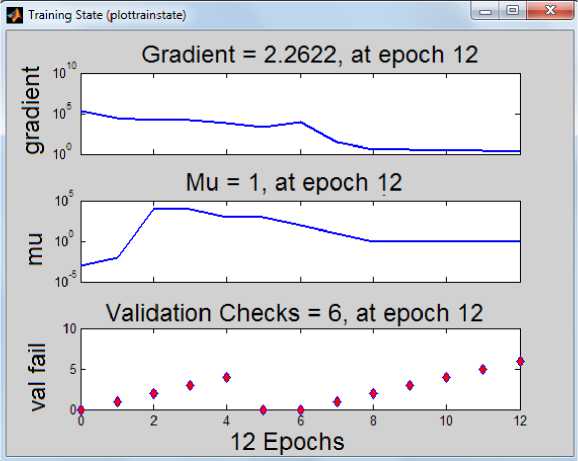
Р и с. 6. Вид обучающей кривой

F i g. 6. The view of training curve

Информатика, вычислительная техника и управление

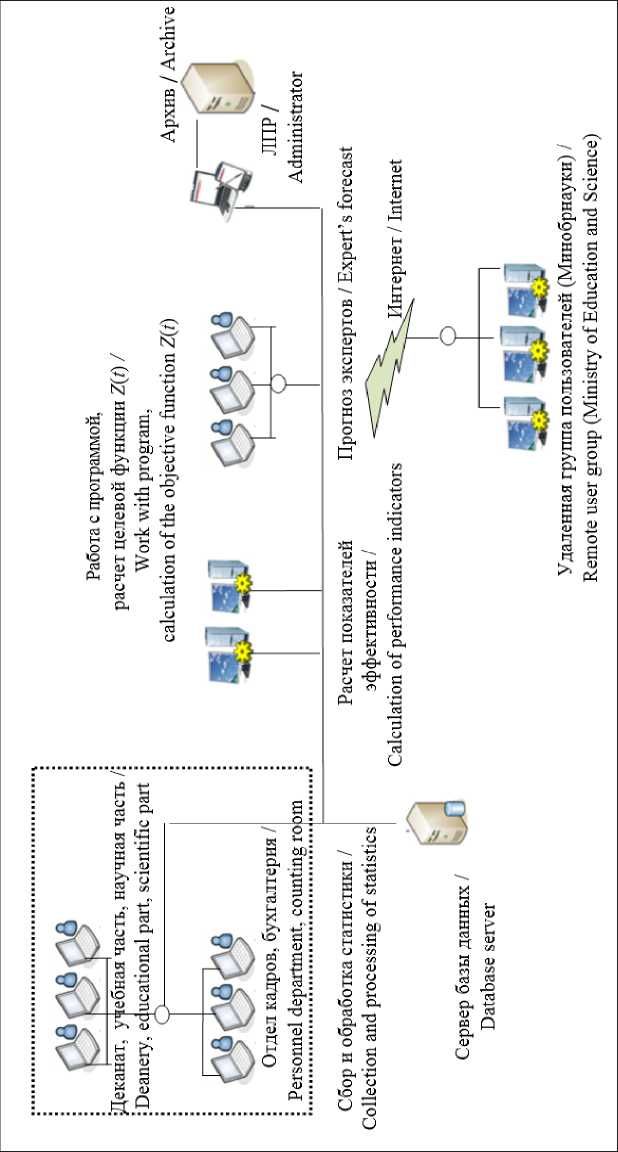
Р и с. 7. Схема проведения мониторинга вуза

F i g. 7. The scheme of the monitoring in the university

^.

10–15 %. Подобный подход к вычислению квадратичного критерия Z ( t ) двумя способами способствует снижению погрешности вычислений и увеличению точности расчетов.

«Модуль для определения эффективности деятельности высшего учебного заведения» предоставляет возможность архивирования вычисленных значений показателей эффективности в базе данных для последующего использования при проведении мониторинга.

Варьируя значения весовых коэффициентов µ_i в зависимости от текущей ситуации, ЛПР получает возможность оперативного управления образовательной деятельностью вуза. На рис. 7 показана схема проведения мониторинга в вузе с использованием разработанного программного обеспечения.

Приведем алгоритм практического применения разработанного математического и программного обеспечения в интегрированной среде вуза.

• 1.    По собранным статистическим данным (отчетам, актам самообследо-вания) формируется массив необходимой информации.

• 2.    Исходные данные формализуются для проведения расчетов, по приведенной методике определяются показатели эффективности образовательной деятельности вуза.

• 3.    Полученные показатели предоставляются в Министерство образования и науки РФ.

• 4.    Рассчитываются прогнозные значения показателей с использованием модели (6) на заданном временном интервале. Возможные сценарии осуществления вузом образовательной деятельности анализируются экспертами с учетом прогнозных значений показателей эффективности.

• 5.    Определяется величина отклонений фактических значений показателей эффективности от пороговых значений (рассчитывается квадратичный критерий Z ( t )) .

• 6.    ЛПР (ректорат, директор, декан факультета) информируется о текущей ситуации в вузе. Если ситуация критическая (в случае значительного отклонения фактических показателей от пороговых значений) определяются возможные направления ее ликвидации.

Том 28, № 1. 2018

Обсуждение и заключения

Разработанное математическое и программное обеспечение может найти широкое применение при мониторинге образовательной деятельности вуза для определения прогнозных значений показателей его эффективности. Это позволит существенно снизить вероятность возникновения критических ситуаций. Созданные модели, методы и программы предоставляют возможность оперативного управления вузом путем сравнения пороговых и фактических показателей эффективности и формирования гибкой образовательной стратегии для конкретного высшего учебного заведения.

Поступила 13.11.2017; принята к публикации 27.12.2017; опубликована онлайн 20.03.2018

Об авторе:

Автор прочитала и одобрила окончательный вариант рукописи.

Сomputer science, computer engineering and management 135

S ubmitted 13.11.2017; revised 27.12.2017; published online 20.03.2018

The author has read and approved the final version of the manuscript.