Моделирование и расчет термохимических характеристик кристаллических оксидов ванадия при стандартных условиях

Ванадий – один из распространенных элементов, который занимает двадцатое место среди элементов, образующихся в земной коре [1]. В самородном виде ванадий в природе неизвестен, так как он относится к рассеянным элементам – в природе его можно найти в виде примесей в различных минералах и горных породах [2]. Важным промышленным источником ванадия служат титаномагнетитовые железные руды и осадочные железные руды. При переработке этих руд ванадий извлекается из шлаков при переделе чугуна в сталь. Другими промышленными источниками ванадия являются: патроитовые, роскоэлитовые и моттрамитовые руды; карнотиты, из которых ванадий извлекают попутно с ураном; окисленные медно-свинцово-цинковые руды, в которых ванадий находится в виде минералов ванадинита, моттрамита и др.

На воздухе этот металл быстро окисляется и при нагревании образует оксиды с различными степенями окисления (VO, V₂O₃, VO₂, V₂O₅ и др.), которые и представляют собой наибольший практический интерес. По данным ряда исследователей [3], в системе V – O существуют от 21 до 25 соединений и фаз. Большинство из них – оксиды V n O 2 n –1 ( n = 2–8), VO 2 , V n O 2 n +1 ( n = 2, 3 и 7) с содержанием кислорода 60 ат. % и более. Эти оксиды хорошо изучены и, как правило, не имеют областей гомогенности. В отличие от них оксиды ванадия с содержанием кислорода менее 55 ат. % имеют широкие области гомогенности.

По свойствам оксидов собран достаточно содержательный экспериментальный материал, но очень часто приводимые данные являются противоречивыми, скорее всего, это зависит от того, что из-за большого количества соединений в системе V – O в качестве исходных объектов исследований выступают очень близкие, а не соответствующие оксиды. Вместе с тем отсутствуют убедительные методики расчета термодинамических характеристик (теплоемкости, энтропии образования) для кристаллических веществ, которые бы соответствовали имеющимся справочным данным. Все вышесказанное осложняет проведение корректного термодинамического анализа реакций восстановления ванадийсодержащих руд.

Целью данной работы стало моделирование и расчет термодинамических характеристик ( С р , S ° ) кристаллических оксидов ванадия произвольного состава при стандартных условиях.

Методика исследования

В силу объективных сложностей экспериментального определения термодинамических характеристик, громоздких расчетов при использовании уравнений статистической термодинамики, учеными постоянно предпринимались попытки создания методов приближенного расчета абсолютной энтропии.

Так, В.А. Киреев предложил метод сравнительного расчета энтропий однотипных неорганических соединений [4]. В.М. Латимер предложил метод расчета энтропии твердых веществ, основанный на аддитивности энтропий составляющих элементов [5]. Ряд ученых, опираясь на накоп- ленный экспериментальный материал по энтропии, пошли по пути установления эмпирических закономерностей, позволяющих рассчитывать ее для неизученных соединений. Так, например, в справочнике [6] предлагается уравнение для приближенного расчета абсолютной энтропии однотипных твердых неорганических соединений.

В работе [7] было проведено сопоставление экспериментальных и расчетных значений абсолютных энтропий на примерах оксидов титана, ванадия, хрома, марганца, железа. Оказалось, что сравнительные методы расчета дают большой разброс результатов в зависимости от выбранного «эталона». В силу отсутствия теоретической базы все рассмотренные методики не универсальны и дают лишь избирательную согласованность с экспериментом. Существующие приближенные методы расчета не учитывают внутреннее строение вещества, не позволяют достоверно оценить энтропию нестехиометрических соединений.

Именно поэтому возникает необходимость в использовании математической модели расчета термодинамических параметров (теплоемкости, энтропии), которая бы удовлетворяла экспериментальным данным. Наиболее корректную модель расчета предложил А.Г. Рябухин. Первоначально модель была разработана для соединений типа Ме y A z , в которых при стандартных условиях Ме является твердым веществом, а A – газом.

В математическую модель расчета термодинамических характеристик автором введены некоторые общие понятия и обозначения [8, 9].

• 1.    Состав бинарных кристаллических соединений Ме y А z приводится к виду ( МеА z/у или МеА x ), т. е. все расчеты ведутся на 1 моль металла в соединении. Подобный прием широко используется при проведении термодинамических расчетов, поскольку позволяет сравнивать свойства соединений разнообразного состава.

• 2.    Теплоемкость (энтропия) сложного вещества складывается из двух независимых величин: С m ( S m ) (индекс от слова mass ), связанной с массой, и С in ( S in ) (от interaction ), определяемой межчастичным взаимодействием:

  
  
  
  

• 3.    Массовая составляющая C m = S in = ^R ln M , где R - универсальная газовая постоянная

• 4.    Поле диаграммы, построенной в координатах C i ^- ( S in ¹) и х, разбивается на n областей квазиравновесных твердых растворов (ОТР). В одну ОТР объединяются соединения, имеющие один и тот же либо близкий тип кристаллической структуры. В каждой области выделяется центральное кристаллообразующее вещество (КО). Полагается, что в рамках одной ОТР зависимость «свойство – состав» носит линейный характер. Обратная величина теплоемкости взаимодействия (энтропии взаимодействия) бинарного соединения определяется из обратных величин С in ( S in ) компонентов с учетом состава и кристаллических структур:

С= С + С "  р тщ ' ^т ;

S = S_m + S in .

(Дж/моль·К); М – относительная атомная масса металла или молекулярная масса соединения, от- несенная к одному молю металла.

C inn ( MeA x ) = C - ( КО ). x x К'--------

K n ^ 2 C n ( А ) + C in ( ^KO )

S in ¹ ( MeA x ) = S in ¹ (KO)_n-------- К⁰--------

K n ₂ S in ( A ) + S in ( KO )

Здесь х _КО и х – отношение числа моль газообразного компонента А на число моль металла в кри-сталлобразующем и в рассматриваемых соединениях соответственно; K n – структурный коэффициент, количественно описывающий изменение структуры внутри ОТР при изменении состава; х n – верхняя (правая) граница рассматриваемой ОТР.

Структурный коэффициент – величина специфическая для каждой конкретной области. Значение K n рассматриваемых областей [8] определяется комбинацией линейных структурных характеристик расположения частиц k соединений, принадлежащих границам областей (либо близ-

Физическая химия

ких к ним). Исходя из того, что верхняя (правая) граница каждой предыдущей ОТР одновременно будет являться нижней (левой) границей каждой последующей области квазиравновесных твердых растворов, логично предположить, что значения k граничных соединений, должны повторяться, то есть быть переходящими от одной ОТР к другой – принцип преемственности.

В пределах одной ОТР уравнения (3) и (4) могут быть приведены к линейному виду. Их совместное решение для смежных областей квазиравновесных твердых растворов позволяет аналитически определить координаты границ х 1–2 , х 2–3 и т. д.

В рассмотренной модели учитывается внутренняя структура соединений, что позволяет корректно рассчитать термодинамические характеристики бинарных соединений во всем диапазоне их составов. Также можно будет уточнить или предсказать величины малоизученных экспериментально соединений.

Результаты расчетов и их обсуждение

Теплоемкость . В системе ванадий – кислород известно более 20 соединений и только для четырех из них имеются надежные справочные данные С ° р . Анализ имеющейся информации по структурам оксидов ванадия показал, что в этой системе должны быть, по крайней мере, две ОТР с ориентировочной границей в районе x = 1,0 (VO).

В табл. 1 приведены исходные справочные данные для оксидов ванадия, являющиеся опорными для проверки математических моделей.

Таблица 1 Исходные данные для расчета молярных теплоемкостей (Дж/моль·K) кристаллических оксидов ванадия, T = 298,15 K

Вещество	Структура	С р , [10]	M
V	куб. (α-Fe)	24,894 ± 0,209	50,942
VO 0,86	–	–	64,701
VO	ГЦК (NaCl)	45,512 ± 0,420	66,941
VO 1,24	–	–	70,781
VO 1,30	–	–	71,741
V 2 O 3 VO 1,5	Гексагональная (α- Al 2 O 3)	104,952 ± 0,314 52,476	74,941
V 4 O 7 VO 1,75	–	–	78,940
V 2 O 4 VO 2	Тетрагональная (флюорит)	115,399 ± 0,419 57,699	82,840
V 2 O 5 VO 2,5	Ромбическая	132,686 ± 0,314 66,343	90,940

ОТР-1: V – VO1,0 (x = 0 –1,0), КO – V

В системе V–O металлический ванадий кристаллизуется в сложной кубической структуре

(α-Fe), низший стехиометрический оксид VO1,0 – в структуре ГЦК (NaCl); отсюда структурный коэффициент K1: K1 = ксл.куб

■ к    = (72 - f) [ -8= + 1 | = 1,05088.

^ГЦК        \зТз    )

ОТР-2: VO 1,0 – VO 2,5 [V 2 O 5 ] ( x = 1,0 – 2,5) , КO – VO 2,5

Во второй ОТР происходит переход от ГЦК структуры, в которой кристаллизуется оксид ванадия (II), к ромбической. В качестве КО выбрано соединение V 2 O 5 , завершающее диаграмму. Величина объемной структурной постоянной K ₂ для ОТР-2 составляет: K 2 = к ГЦК ■ к ромб = ( V2 - 1 ) - 276 = 2,07345.

Тогда уравнение (3) для ОТР-1 и ОТР-2 соответственно окончательно принимают вид:

Г (\м _х ) = 011690 — 0 , 081286 х ;                               (5)

C ^-1 ( VO _х ) = 0 , 04439 - 0 , 009502 х .                                (6)

Результаты расчетов по уравнениям (5) и (6) приведены в табл. 2 и на рис. 1.

Из сравнения экспериментальных данных и расчетных величин молярных теплоемкостей оксидов ванадия можно сделать вывод, что данные хорошо согласуются с экспериментальными данными и не выходят за пределы доверительных интервалов последних.

В табл. 2 представлены оксиды ванадия, о которых есть упоминания в литературе, но отсутствуют данные по теплоемкости. Применение гиперболической модели А.Г. Рябухина позволило предсказать для них величины стандартных молярных теплоемкостей.

Таблица 2

Результаты расчета молярных теплоемкостей (Дж/моль·K) кристаллических оксидов ванадия, T = 298,15 K

Вещество	c m	Сin , ур. (1)	С in ,ур. (5), (6)	С рP , ур.(1)
V	16,3399	8,5541	—	—
VO 0,86	17,3338	—	21,2793	38,6131
VO	17,4752	28,0368	28,0788 28,6632	45,554 46,1384
VO 1,24	17,7071	—	30,6678	48,3749
VO 1,30	17,7631	—	31,2135	48,9766
V 2 O 3 VO 1,5	17,9445	34,5315	34,1818	104,6526 52,1263
V 4 O 7 VO 1,75	18,1606	—	36,0211	216,7268 54,1817
V 2 O 4 VO 2	18,3611	39,3384	39,3918	115,5058 57,7529
V 2 O 5 VO 2,5	18,7489	47,5941	47,4614	132,4206 66,2103

Совместное решение уравнений, которые описывают зависимости обратной теплоемкости от состава оксидов ванадия для граничащих областей твердых растворов ОТР-1 и ОТР-2, позволяет аналитически определить состав границы между областями. Так, из уравнений (5) и (6) находим x 1–2 (VO х ) = 1,01011, что близко к составу соединения VO и подтверждает правильность выбора границ.

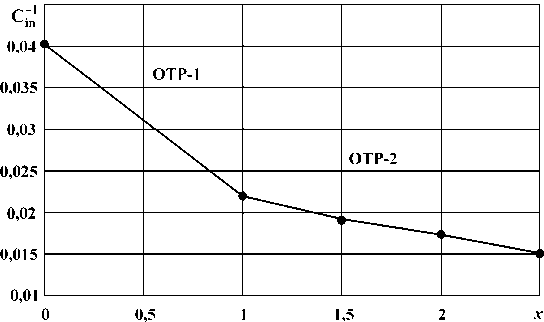
Рис. 1. Зависимость обратной величины стандартной молярной теплоемкости от состава оксида, отнесенной к одному молю ванадия (• – теория, __ – расчет)

Энтропия . Кислород является составной частью любого оксида. Образованию оксида предшествует процесс адсорбции, при котором кислород (и другие двухатомные газы – H 2 , F 2 , N 2 и т. д.) диссоциирует на атомы. Адсорбированные атомы находятся не в свободном состоянии, а сразу вступают в химическое взаимодействие с металлом или диффундируют через оксид. Энтропия взаимодействия для атомов кислорода, входящего в состав оксида, рассчитывалась как

S° n ( о ) = 1 s ° ( O₂ ) - s m ( о ) = ¹ s ° ( O₂ ) - 1 R In M = 102,0735 - 11,5255 = 90,548 .

Физическая химия

Анализ экспериментальных данных по системе V – O (табл. 3) позволил считать, что поле диаграммы S ^- - x содержит две области: первая включает соединения с кубической структурой, а вторая – более сложные (гексагональную, тетрагональную и ромбическую).

Таблица 3

Экспериментальные данные и результаты расчета молярных энтропий (Дж/моль·K) кристаллических оксидов ванадия, T = 298,15 K

Вещество	S , [10]	Sm	S in , (ур. 2)	S - 1 Sin	s - , ур. (7), (8)	S, (ур. 2)
V	28,640 ± 0,33	16,3399	12,3301	0,08110	—	—
VO 0,86	—	17,3338	—	—	0,06489	36,6485
VO	38,995 ± 0,42	17,4752	16,0648	0,06225	0,06225	38,7518
VO 1,24	—	17,7071	—	—	0,04736	43,4697
VO 1,30	—	17,7631	—	—	0,04364	44,9592
V 2 O 3 VO 1,5	99,788 ± 1,3 49,894	17,9445	31,9495	0,03129	0,03127	50,1333 49,9123
V 4 O 7 VO 1,75	—	18,1606	—	—	0,02881	52,8708
V 2 O 4 VO 2	113,512 ± 1,3 56,756	18,3611	38,3949	0,02605	0,02633	56,3406
V 2 O 5 VO 2,5	131,048 ± 1,3 65,524	18,7489	46,7751	0,02138	0,02138	65,5161

ОТР–1: V – VO1,5 (x = 0 –1,5), КO – V:

Кристаллообразующим в первой области выбран ванадий, который кристаллизуется в кубической структуре (α-Fe). Оксид ванадия (II) кристаллизуется в структуре в ГЦК (NaCl), а оксид ванадия (IV) в гексагональной. Отсюда структурный коэффициент K 1 равен: K 1 = к куб • к гекс = ( 2 - 1 ) - 383 = 0,28505.

ОТР–2: VO 1,5 – VO 2,5 ( x = 1,5 –2,5), КO – VO 2,5 :

В данной ОТР за кристаллообразующий можно выбрать хорошо изученный V2O5 с ромбиче- ской структурой. Тогда переходу от гексагональной структуры к ромбической будет отвечать коэффициент K2: K2 = кгекс

• К г — ------ • ромб

-2= = 0,73557.

Тогда уравнение (4) для ОТР-1 и ОТР-2 соответственно окончательно принимают вид:

S - ( VO x ) = 0,08110 - 0,03410 х ;                            (7)

S in ¹ ( VO x ) = 0,04613 - 0,00989 х .                                 (8)

Результаты расчетов по уравнениям (7), (8) приведены в табл. 3 и на рис. 2.

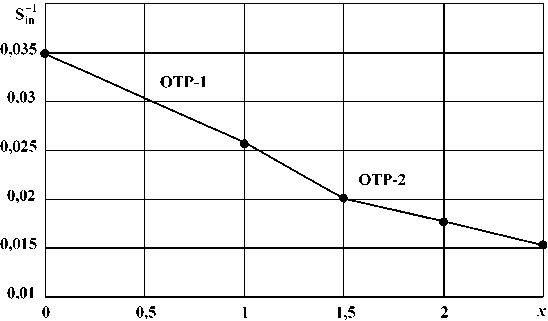
Рис. 2. Зависимость обратной величины стандартной молярной энтропии от состава оксида, отнесенной к одному молю ванадия (• – теория, __ – расчет)

Совместное решение уравнений, описывающих зависимости обратной энтропии от состава оксидов ванадия для граничащих областей твердых растворов ОТР-1 и ОТР-2, позволяет аналитически определить состав границы между областями. Так, из уравнений (7) и (8) находим x 1–2 (VO х ) = 1,4949, что близко к составу соединения VO 1,5 и подтверждает правильность выбора границ.

Заключение

Гиперболическая модель расчета молярной теплоемкости и молярной энтропии проверена на стехиометрических оксидах ванадия. Наблюдается хорошее согласие полученных результатов с экспериментальными данными. В расчетных уравнениях используются термодинамические параметры (теплоемкость, энтропия) простых веществ (металл, кислород) и их стехиометрических соединений с учетом структурных постоянных.

Подтверждена эффективность предложенного принципа преемственности линейных характеристик k граничных соединений при определении структурных коэффициентов K_n областей квазирав-новесных твердых растворов для расчетов молярной теплоемкости и молярной энтропии.

Использованная математическая модель позволяет уточнять значения известных термодинамических параметров (молярная теплоемкость, молярная энтропия) и предсказывать численные значения для малоизученных экспериментально соединений для ряда бинарных кристаллических веществ одинакового качественного состава.