Моделирование и расчёт шероховатости поверхности при точении резцами со вставками из композитов

однако в настоящее время отечественное производство и потребление не превышает 5% от указанной потребности. Одним из определяющих условий преодоления этого отставания является применение современного точного высокоскоростного оборудования.

При создании нового технологического процесса или при выборе формы и геометрических параметров режущего инструмента со вставками из композита возникает необходимость прогнозирования в автоматизированном режиме параметров шероховатости обработанной поверхности. Формализовать расчёт параметров шероховатости Rz и Ra возможно с учетом геометрических и кинематических факторов, приравнивая параметр Rz к теоретической высоте остаточного гребешка h 1 . Величина h 1 – ордината точки с , пересечения прямых (рис. 1), одна из которых – касательная к окружности радиуса r ¹ в точке а , а вторая – касательная к окружности радиуса r в точке b . Причем, r = r ¹ на смежных витках траектории с шагом, равным подаче S . Остаточный гребешок формируется главной режущей кромкой – часть дуги радиуса r и отрезок bc , а также вспомогательной режущей кромкой – часть дуги радиуса r ¹ и отрезок ас . Формулы (1), (2), (3) для расчета ординат точек с и f, предложенные в работе Сусловым А.Г. [1], учитывают искажения высоты остаточного гребешка при наличии положительного переднего угла.

Ордината точки с:

tg^ • tgф       r y S 1        +     1

tg ф + tg ф   tg ф + tg ф

tg ф I 1-- 1 + tg ф l 1 -

( cos ф)     (

cos ф¹

Ордината точки f :

y1 = r (1 - cos ф) + S • sin ф cos ф - sin фS • sin ф (2r - S • sin ф)

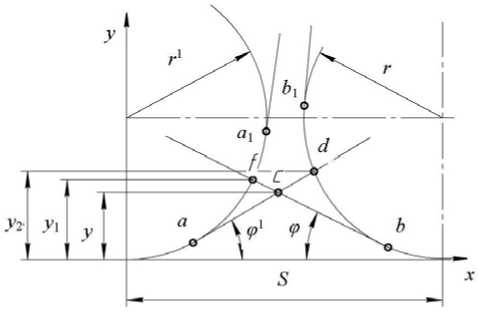
Рис. 1. Схема для расчета геометрической составляющей шероховатости поверхности

Высота остаточного гребешка h1=y1. В случае, когда точка b находится в положении b1, остаточный гребешок ограничивается частью дуги радиуса r1, отрезком ad и дугой радиуса r (при ya < у и yb1 > y). Высота h 1 =y2 рассчитывается по формуле (2), но угол ф заменен на угол ф y2 = r (1 - cos ф ) + S sin ф cos ф1 - sin ф1 ^S sin ф (2r - S sin ф1)

.

Алгоритм расчёта Rz=h 1 на ЭВМ представлен на рис. 2.

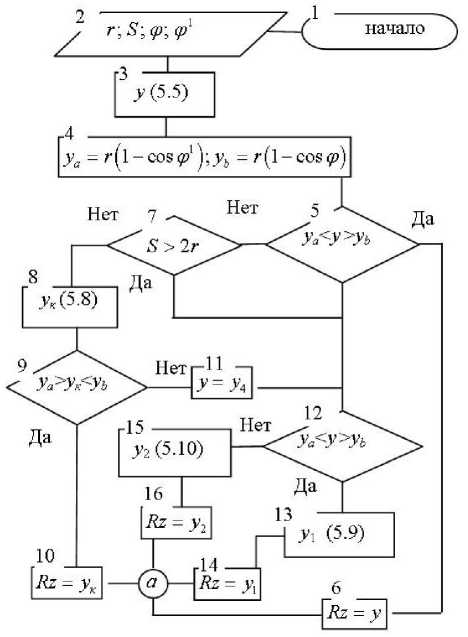
Рис. 2. Алгоритм расчета высоты остаточного гребешка или профиля

Геометрически шероховатость формируется при сочетании геометрии лезвия и подачи, однако это не окончательная форма микрорельефа, поскольку происходит искажение за счет пластических деформаций [2, 3]. Если ось х перенести на среднюю линию профиля поверхности, то среднее арифметическое отклонение профиля можно определить по формуле

Ra =

1 f xa                 xb

- J| У ( x )| dx + J| y ( x )| dx + ... + l (

J |y (x )| dx xn

где l – длина базовой линии; х a , х b , …, х n – координаты, которые ограничивают функцию у ( х ) на оси х . Уравнение окружности радиуса r при таком перенесении оси х приобретет вид

( Rz Y _{2   2}                     Rz 2----2

( У ^- r ⁺ уJ ^{+ x} = ^r. Тогда У = r ^- у ± r^{T x} x , а площадь под дугой, ограничивающей соответствующий участок шероховатости x ₂

f Rz у 2" | д

FK = r--— rr -x dx к 2             . После преобразований:

x

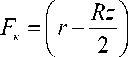
x ₂ x ₁

r ² xx 2

--arcsin —

2 r x ₁

^^^^^^^B

x_r 2

^^^^^^^B

x ²

x ₂ x ₁

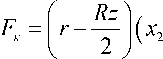
^r f x x । x          x

- x^ ) -    arcsin — - arcsin— —-rr - x₂ +—J r - x j

¹⁷ 2 I r r ) 2 ^{v 2} 2 ^{v 1}

Это выражение позволяет определить площади F ₁, F ₂, F ₃ (табл. 1), ограниченные дугой окружности радиуса r.

По этой же формуле можно найти и площади F 4 , F ₅, F ₆, ограниченные дугой радиуса r ¹, если вместо значений х ₁ и х ₂ подставлять координаты начала и конца дуги, уменьшенные на

величину S. Тогда площади F ₉, F ₁₀, F ₁₁, которые ограничиваются вспомогательной режущей кромкой, определяются по формуле:

x 2 ( С

F . Х( r (1 - x 1 V V

-----г 1 + xtg ^ cos ф )

Rz

-

dx

Таблица 1. Формирование среднего арифметического отклонения профиля

№	Схема отклонения профиля поверхности от средней линии	Условия создания слагаемых площади шероховатости
1	у.       Fs	y a < Rz ; у ь < Rz ; y a < Rz /2; у ь < Rz /2; F = F 1 + F 7 + F 8 + F 9 + F 10 + F 4
2	^8 C /10 ^^7 x 8Х=У	y a < Rz ; у ь < Rz ; y a > Rz /2; у ь > Rz /2;     , F = F 2 + F 3 + F 12 + F 11 + F 6 + F 5
3	Ух         Л §МН" /’	y a > Rz ; y b > Rz ; F = F 2 + F 3 + F 6 + F 5
4	„     р п р У 1 р * 1       У 9 р р I                                 / 0 / 4 I    / Г3 у^' ^1 Х —7   Б^=А	y a > Rz ; y b < Rz ; yb < Rz /2; F = F 2 + F 3 + F 9 + F 10 + F 4
5	у           И /11 '   /2 ^Vxb^v F5	y a > Rz ; y b < Rz ; y b > Rz /2; F = F 2 + F 3 + F 11 + F 6 + F 5
6		y a < Rz ; y b > Rz ; y a < Rz /2; F = F 1 + F 7 + F 8+ F 6 + F 5
7	Г     Х^   '	y a < Rz ; y b > Rz ; y a > Rz /2; F = F 2 + F 3 1 + F 12 + F 6 + F 5

x

F. = J( r (1 -AV 4 | ( x 2 - X 1 ) + ^ cos ф 2             2

.

x 1 V             ^ф V 7

Площади F ₇, F ₈, F ₁₂, ограниченные главной режущей кромкой, определяются по формуле:

F r =Jk I¹ - x i V v

cos ф

Rz I - xtg ф + Stg ф - — I dx

x2 I I,       1 I Rz I               tgф 22

^Fr = J I r l ¹ i" |^-^T ⁺ ^^{8 ф} I⁽ x ² "  x 1 ) ' T ( x 2 "  x 1 )

cos ф 22 xi v/

Координаты начала и конца линий, которые ограничивают характерные участки площади на схеме для определения Ra , равняются

ya

^^^^^^e

r 1

^^^^^^^

Rz

xa

cos ф¹

^^^^^^e

Rz

^^^^^^^»

^^^^^^^B

tg^1

x d =

r

^^^^^^e

cos ф

Rz - r

-

;

tgф'1

x _c

cos ф¹

;

?дф'

;

x _e

r 1

^^^^^^^B

cos ф

+ Stg ф

- y_b ^{+ r}

^^^^^^^B

xg = S "I ^r2

^^^^^^^B

tg ф

xb =

cos ф

+ Stg ф

;

tg ф

^xf =

r ²

Rz

^^^^^^B

;

;

;

.

Определяем все слагаемые любой общей площади (см. табл. 1) в соответствии с одной из схем расчета Ra (рис. 3):

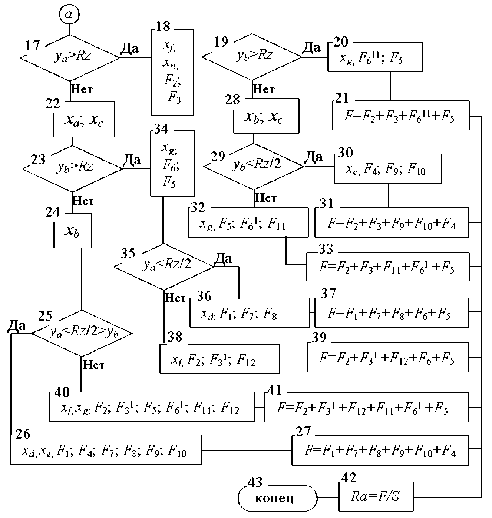
Рис. 3. Алгоритм расчета среднего арифметического отклонения профиля

Площадь F изменяется в пределах подачи S и периодически повторяется при любом значении l, поэтому для определения среднего арифметического отклонения профиля достаточно разделить F на S.

Геометрически шероховатость формируется при сочетании геометрии лезвия и подачи, однако это не окончательная форма микрорельефа, поскольку происходит искажение за счет пластических деформаций [4]. При больших скоростях резания на многоцелевом станке

VH4000, когда пластические деформации незначительны, расчетные значения параметра шероховатости Ra (рис. 4, кривая 1) практически совпадают с экспериментальными (рис. 4, кривая 2). Материал инструмента – композит Ко, обрабатываемый материал – сталь 30ХГСА. С увеличением пластической деформации в зоне резания (при понижении скорости резания) экспериментальные значения Ra отклоняются от расчетных (рис. 4, кривые 3, 4) [5, 6].

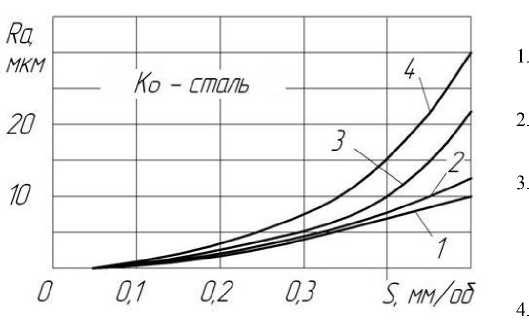
Рис. 4. Расчетные(1) и экспериментальные(2, 3, 4) зависимости параметра шероховатости от подачи при различных скоростях резания:        ^5.

D _заг =40 мм; t=0,3 мм; 1,2 – V=249 м/мин; 3 – V=178 м/мин; 4 – V=49 м/мин

Вывод: предложенный алгоритм расчета геометрической составляющей высоты микро- ₆ еровностей и среднего отклонения профиля по-    ^.

верхности полностью автоматизирует процесс и исключают предварительный анализ ограничивающих условий.