Моделирование и сравнение результатов точного аналитического решения краевой задачи течения в тонком слое с экспериментальными данными

EDN: LLYQKW

Постановка и решение краевой задачи. Пусть достаточно тонкий слой металла деформируется параллельно движущимися навстречу друг другу плоскими инструментами, как показано на рис. 1. В качестве допущений примем [1]:

• -    плоскости контакта инструмента являются шероховатыми;

• -    материал инструмента абсолютно жесткий;

• -    деформируемый слой из идеально пластического металла.

Кроме того, течение по координате y=±b ₀ отсутствует, т.к. контейнер матрицы имеет боковые стенки (рис. 1 б).

Краевая задача растекания на шероховатой плоскости слоя из пластического материала формулируется следующим образом [2, 3]:

ар —	□= at . — — Ди - з ал	2ts	и
ах		h	^u2+v2'
ар _	as at . — Ди - з ал	^ts	V
ау		h	^u2+v2'
аи ,	ар ал	0,
--И
ах	ау at

где р,и, v - давление на контактных поверхно-os стях и компоненты вектора скорости; Ts -уЗ

– сдвиговые напряжения материала пластического слоя; h — h(t) - зависимость изменения толщины слоя от времени;

^h(^t o ) ^{w) —}'"адт

A(t) - степень деформации по А.А. Ильюшину; t₀ – время начала процесса деформирования.

Примем на свободной границе образца, обозначенной как r_c\F(x, у, t) — 0 , положение которой заранее неизвестно, краевые условия:

одно динамическое

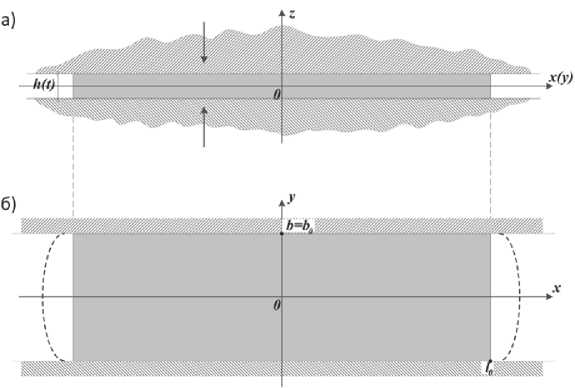
Рисунок 1. Схема течения сборного образца: а - разрез плоскостью, проходящей через ось z; б - вид сверху

5⁽ⁿ⁾ = стп = 0, заменив его двумя скалярными, получим:

^ хх ^П х ⁺ ^ ху ^П у ⁰ ^ уу Н у ⁺ ^ ху ^ х ⁰, где нормальный к границе вектор:

VF и= (пх,Пу) = —, при этом не нулевые компоненты тензора напряжений 5 будут иметь вид:

О ХХ = ~Р + 1 ^ 5

Кроме динамического условия непроницаемостью границ:

+ -Os^^^r">^axx> =   (^ + ^^уу = ~Р + ^У°$ + ^У ^s^l^

3 5 dX дх х^   3dX ду дх уу          3 s 3 s dXдy

■

(4), требуется задать одно кинематическое, обусловленное

dF/dt v„ = v ■ п =-- n               \gradF\

По условию (8) можно восстановить интересующую нас границу Г_с . Обозначим контактную поверхность с инструментом через r_k:G(x,y, t) = 0 , на которой реализуются также два условия: одно динамическое, диктуемое равенством тангенциальной составляющей вектора напряжения предельному значению при факторе трения д = 1 :

|(? C ⁿ⁾ ■ f| = \^ хх П х П у + О ху (п у - п х ) - О уу П х П у \ = ^,(0 < Д < 1)

и второе кинематическое, обусловленное непроницаемостью контактных поверхностей инструмента (10):

dG/dt n -            \gradG\’

где f = (п_у,-п_х) и п - единичные касательный и нормальный векторы к границе Г_к . Если граница неподвижна, то компонента нормальной скорости равна нулю.

Для решения системы (1)-(3) течения пластического слоя с подвижными и неподвижными границами выписанных условий (7)-(10) вполне достаточно.

Для перехода к безразмерному описанию задачи определим значения характерной длины Zo, скорости сближения плит деформирующих инструментов vo, контактного давления р0, толщина слоя обезразмеривается на h0, время - на —. Относительную толщину пластического слоя Fo е = -° << 1 примем за малый параметр.

^l o

Проведем оценку порядка последних величин, исходя из простейших уравнений математической модели растекания тонкого слоя из пластического материала.

Уравнение равновесия (1) при у =0

запишем в безразмерном виде

^д® хх + 2t_s _ о дх h

^д£ хх ( Р о \+ ^£₁ ^ ^ ₌о^ дх   l_o      h h_o

и

Следовательно,

P o Ъ

— ~ — ,или P o ~

Os P q _~

Рассмотрим, далее условие несжимаемости (2)

ди । 1 dh _ ^ дх h dt '

Следовательно,

Очевидно, что

as    as

ftp'

(dh dt    dh(to)_0

dh(t0) у dt ’ du v0    1 dh ho dh(t0)

dx l₀ ⁺ h dt   l₀ dt

и0   1 dh(to)

l0 h0 dt

dh(t₀) 1 ^ o --7- dt 8

Приведем уравнение несжимаемости (13) к безразмерному виду du /Vq\ 1 /Ц dh⁽t o ⁾ ho ₌ dxXlJ h\h_o) dt t_o~ '

После подстановки у и сокращения, получим, что

^ D _£ ^l o ^t o

и окончательно

t     lo

'

Будем считать, что

lo            dh(t0) 1

^{t o _}< ^{V q _}   dTE

Сравнение величин характерных скоростей приводит к утверждению, что скорость сближения инструментов заметно отстает от скорости течения слоя и это является прогнозируемым. Оценим порядок слагаемых в квазистатических уравнениях равновесия. Очевидно, что давление на контакте (12) при возрастании, превышает предел текучести материала слоя.

Полагая, что толщина слоя h , в отличие от других линейных размеров (координат), при делении на h(t_o) становится безразмерной, перепишем в безразмерном виде систему уравнений (1) - (3):

др dt -г— Тх^_£Т^^и др dt -г— ^^_£ dx ^Av

—

—

^+ д/ —^_о, дх ду dt

2 U

V3hVu²+v² '

2 V

Рзк^й²+5² '

где безразмерные величины отмечены диакритическим знаком «верхняя черта» (заметим, что в уравнениях равновесия при слагаемых со старшими производными - лаплассианами появился малый параметр е ).

Граничные условия поставленной задачи преобразуем следующим образом. На свободной границе f_F:F(x,y,t) _ 0 при отсутствии напряжений (4):

_ /2 2dtdu\   _     1dt/du dv\ _       _ /2 2 dt du\

° ^{хх     P} \3 3d2dx)^£,°^xv 3d2\dy dx/^{,( ryy     P} \3 3dAdy/'

С учетом безразмерного вектора (6) нормали к границе: _^   gradF

\gradF\ скалярные условия (5) после обезразмеривания приобретут вид

[—p + (^- + -^dP] u_x + p-d- ( ди + дР] u_y _ o, 3   3 dX дх ^х 3 dX ду дх У ’

г idt au av                    2   2dtau

[ 351 U ⁺ aJ^£J^п * ⁺ г^{р + (} з ⁺ заз^г ! ^п у ^- °-                      ⁽¹⁸⁾

Кинематическое условие (8) для восстановления границы Г_Е преобразуется:

v „ -

∂F∂t lsradF| -

На контактной границе слоя с инструментом Г_к динамическое условие (9) в безразмерном виде:

аххПхПу + стху(пу2 щ.2) - СТууПхПу| - V=£(2°)

или

2 2dt"au              Idt au av 2 „2             2 2^95д г?+ (з+ заз^г! n*ny+ [заз(a? + мг1 (ny-    - rp + (з+ 3dia^aJ£J n*ny- ±V3£. (21)

Условие непроницаемости поверхности инструмента (10) определится как (22):

∂ G ∂ t

V„ ---:-^,

„ |gradG|

В итоге два дифференциальных уравнения в частных производных (14), (15) квазистатического равновесия и условие несжимаемости (16) вместе с граничными условиями (17) - (22) составляют общую краевую задачу течения пластического слоя в модели «вязкой жидкости» [4, 5].

В главном приближении, когда отсутствует малый параметр (£ - °), исходные уравнения упрощаются с понижением порядка системы:

ap _    2t_s u

ax “  V3%Vu ²_ +v ² '

ap      2ts v ay     V3d Vu2+v2 '

^ + ^-^-°- ax ay dt

Надо заметить, что большинство исследований в указанной области проводились на основе упрощенной постановки краевой задачи в модели «идеальной жидкости», которая описывается нелинейными дифференциальными уравнениями в частных производных первого порядка [2, 6].

В эту модель входят уравнения квазистатического равновесия (26) и (27): ap _    2t_s u

ax      d Vu ² +v ²

ap _   2ts v ay       d ^u2+v2’ а для избавления модели от статической неопределимости в систему следует добавить условие несжимаемости (3).

Логично, что граничных условий в упрощенной задаче в модели «идеальной жидкости» требуется меньше, а касательными напряжениями пренебрегают. В этом случае краевые условия имеют вид:

Р - O's, если деформирующий инструмент содержит пазы, куда свободно затекает металл, то

Р - 2щ, а в случае, если на границе пластического слоя и инструмента течение затруднено, то

Р - Рг№ где ^ - параметр вдоль контура области.

Из двух уравнений (26) и (27) последней системы нетрудно получить одно нелинейное дифференциальное уравнение относительно контактного давления:

(йЛ®^^-# которое вместе с граничным условием (28) или (29), или (30) представляет краевую задачу относительно контактного давления.

Исследование кинематических параметров течения пластического слоя по упрощенной модели обеспечило возможность вывода эволюционного уравнения, с помощью которого устанавливают свободную границу растекающейся области [7].

Краевая задача течения пластического слоя в новой постановке предполагает введение функции тока ф - ф(х,у), которая не противоречит условию несжимаемости (3). Преобразованные компоненты скоростей (32)

и-^+Ф-—£(*— У ).

подставим в квазистатические уравнения равновесия и в результате получим систему из двух дифференциальных уравнений (33) и (34) относительно контактного давления р и функции тока у :

р £ - ⁽-у^)д ^ у _    2т ₅ Ф у + т7

рУ+(У)дФ£

h т ^У 2

fc — ^)^ — ^

Далее рассмотрим в натуральных величинах задачу течения пластического слоя, имеющего в начальный момент деформирования форму прямоугольника в плане (см. рис.1). В силу симметрии пластической области относительно выбранной системы координат, будем работать с элементом слоя, расположенным в первом квадранте. На неподвижной стенке инструмента при координате С⁽х,у⁾ = у —b o - 0 :

v - 0 ^ ф Х — -2 ⁰ - 0, £ + £ - —^ - ф УУ — ф ЛХ - —Тзл ' щ

Краевые условия:

у - 0: V - 0 ^ ф Х - 0;

х - 0: и - 0 ^ ф у - 0;

На неизвестной свободной границе F (x, y, t) =0, х - Z₀(n_x - 1,п_у - 0) , краевые условия определяются:

У ⁰ -УУ ^ 0 , ф" в начальный

- 0

- 0

момент имеющей параметры

ст_гг - 0 ^ —р + щ + ²щ ф '' - 0; щ., - 0,ф₁','₁, — ф" - 0. лл                  о 3 ^ лу        лу УУ лл

Для нивелирования влияния краевых эффектов будем искать аналитическое решение задачи на некотором удалении от оси х - 0 и от свободной границы х - 0,5Z_O , поскольку протяженность области течения в направлении x позволяет это сделать. Для рассматриваемого участка области течения компонента скорости v (х, у) - 0. После интегрирования уравнения несжимаемости (36) получаем:

и⁽х,у⁾ -Л ' ^[х + д(у)^], где функцию д(у') можно определить из других уравнений системы: (2) дает р - р(х) и тогда из (1) следует (40):

р ' (х)-^ — ЗЦ, 3   V3 h

где в левой части стоит функция аргумента х , а в правой - функция у и параметр K(t), другими словами, имеем дифференциальное уравнение с разделяющимися переменными. В итоге получаем систему с произвольной постоянной, представляющей собой функцию времени к:

д'^у) - к - const; р ' (х) - ^ — ЗЦ.                            (41)

После нахождения решения дифференциального уравнения первого порядка с разделяющимися переменными (41) после подстановки граничных условий (37), (38) получим:

дм - с—з£у²,к - 2- о

—

Уз _м Ь о ^,

и(х,у) - Л ' [х — ^у² + с],

где с - постоянная интегрирования.

Заметим, что первое слагаемое в правой части уравнения (43) соответствует скорости течения в модели «идеальной жидкости», в рамках которой касательное напряжение на неподвижной границе, равное 0, как и на других границах, отсутствует. Положим, что сечение х - х ^ представляет собой условную свободную границу ( х ^ К - х₀К₀ ). Тогда из интегрального условия сохранения объема несжимаемого материала

- о

dK

—хДО —bo- I hu^_xf,y)dy определяем входящую в решение произвольную постоянную с - — дЬ0, что дает возможность 6

получить окончательную формулу для скорости течения:

и⁽х,у⁾ - Л ' [х + -^- (pbo² — Зу²)] . 6Ь о

Сопоставлением найденной скорости (44) и граничного условия (30) при значении х = О убеждаемся, что оно выполняется в интегральном виде:

b °                          ь °

[ u⁽0,y⁾dy =-77- [ (Ь₀² - 3y ² )dy = О.

6о0

0                          0

Из второго уравнения (41) после интегрирования получим (45):

^р(х) = ^р 0 ^-2б( ^{2 +} "Й-

с постоянной интегрирования р₀ , не зависящей от координаты у. Полагая, что на свободной границе нормальное напряжение равно нулю:

о*х = -р + ^ = О находим

^{P o (t)}   V3h ⁺(vXb o ⁺ з^

При достаточно большом x_f третьим слагаемым в правой части можно пренебречь, тогда окончательно постоянная интегрирования примет вид a_sx 2 ц \

P 0 ^(t) = ^r(-_h⁺ 3

В результате искомое значение давления найдем в соответствии с результатом в (45): ^p~M ^{2 +}9i^x f ^-xi                           ⁽⁴⁶⁾

В заключении определим вид функции тока:

Ф Х = ^У; Ф у = ² + ^(^рЬ0² - ³У²) ^ Ф⁽х,У⁾ = ^7(цЬ0²у-3у³) + С 1 .          (47)

2          2 оО °                                    ои °

Таким образом, в рамках общей модели «вязкой жидкости» получено приближенное аналитическое решение. На границе х = О , а также на свободной границе х = x ^ (t) оно удовлетворяет краевым условиям в интегральной форме. Следовательно, согласно принципу Сен-Венана, решение справедливо в центральной части области течения. Характер течения в слое не является одномерным, поэтому прямые линии (х = const) с течением временем искривляются, причем наблюдается заметное отставание продольного перемещения частиц вблизи неподвижной границы. Этот факт подтверждается результатами проведенных экспериментов. Полученные закономерности невозможно описать с помощью модели «идеальной жидкости», в которой не учитываются касательные напряжения.

Результаты экспериментальных исследований . Для оценки влияния осредненных по толщине слоя касательных напряжений на кинематику течения в эксперименте необходимо обеспечить условия затрудненного течения пластического слоя, что достигалось конструкцией инструмента, а именно матрица имеет противоположные неподвижные стенки (рис. 2), ограничивающие течение плоского образца, имеющего прямоугольную форму, вдоль длинных сторон. Образцы выполнены составными из двух полос толщиной 2 мм. Размеры в плане: длина 21₀ = 7Омм , ширина 2Ь₀ = 25 мм , и суммарная толщина Л₀ = 3мм . Материал образцов свинец марки С0 ГОСТ 3778-98 [8]. Для того, чтобы нанести координатную сетку на одну из плоскостей полосы, были изготовлены пары тонких полос с толщинами Z₀₁ = Z₀₂ = 2 мм, и на поверхность одной из них с помощью инструментального микроскопа УИМ-21 наносилась координатная сетка с шагом М = 2 + О,О1 мм (рис. 3).

Были проведены две серии экспериментов. Полоса деформировалась в оснастке так, что в процессе осаживания размер r 0 оставался неизменным.

В результате проведенных экспериментов по сжатию образцов между сближающимися жесткими плоскостями инструментов установлены экспериментальные закономерности. С помощью этих закономерностей можно оценить корректность выбранной математической модели, которая может быть использована для описания течений.

Рисунок 2. Штамповая оснастка

Рисунок 3. Исходные свинцовые образцы

полос, на которые нанесена координатная сетка

В каждом отмеченном рисками сечении X = const отслеживали поле перемещений.

а )

Рисунок 4. Координатная сетка после

б )

деформации (^ = 0,з) :

a - система координат (линейка показывает только масштаб);

б - участок сетки с 4-х кратным увеличением

Смещения узлов координатной сетки после деформирования измеряли с точностью 0,01 мм на инструментальном микроскопе УИМ-21 с определением минимального значения перемещения н_й(Х) = u(X;Y = у) вблизи неподвижной границы (y = у) и максимального значения u_m(X) = u(X; Y = 0) в средней по ширине точке ( Y = 0 ) (рис. 4). Затем вычисляли абсолютную ^u = и_т(Х) - и_ь(Х) и относительную ^“^ величины перемещений в характерных сечениях X = const .

Результаты измерений и значения оценок внесены в табл. 1 и табл. 2.

Таблица 1 . Перемещения в сечении X = const: h_T = 2,8 мм; Ah_x = h₀ - h_T = 1,2 мм; F = 200 кН

X	um(X)	u5(X	Au(X) = = um(X) — U S (X)	Au(X um(X)
0	0	0
4	2,43	1,92	0,52	0,21
8	3,93	3,29	0,64	0,16
12	6,16	4,95	1,21	0,19
16	8,10	6,68	1,42	0,17
20	9,93	8,07	1,86	0,19
24	11,90	9,54	2,36	0,20
28	14,05	10,60	2,45	0,24
32	16,05	11,51	4,64	0,28

Таблица 2. Перемещения в сечении X = const-. h₂ = 2,6 мм; Ah₂ = h₀ - h₂ = 1,2 мм; F = 310 кН

X	u m (X)	u5(X)	Au(X) == um(X) — U 5 (X)	Au(X) U m (X)
0	0	0
4	3,05	2,64	0,41	0,13
8	5,40	3,92	1,48	0,28
12	7,98	6,08	1,90	0,24
16	8,38	7,03	1,35	0,16
20	12,27	10,34	1,93	0,16
24	14,35	12,04	2,31	0,16
28	16,94	14,06	2,88	0,17
32	19,12	17,45	2,54	0,13

Анализ экспериментальных результатов подтверждает заметное отставание продольного перемещения частиц вблизи неподвижной границы: вертикальные в начальном состоянии риски ( X = const ) перестают быть прямыми в процессе осадки полосы. Поэтому экспериментальные закономерности невозможно корректно описать с помощью модели «идеальной жидкости» (26), (27) и (3), в которой пренебрегают касательными напряжениями. Для рассматриваемого случая воспользуемся граничными условиями:

у = 0; v = 0;

у = b_Q; v = 0;                                              (48)

х = 0; и = 0, а на свободной границе справедливо (28).

Решение системы уравнений краевой задачи имеет следующий вид: кинематические параметры:

^v = ⁰; ^и = ^— “х                                 ⁽⁴⁹⁾

контактное давление:

Р = —ДКх —“А 4                   (50)

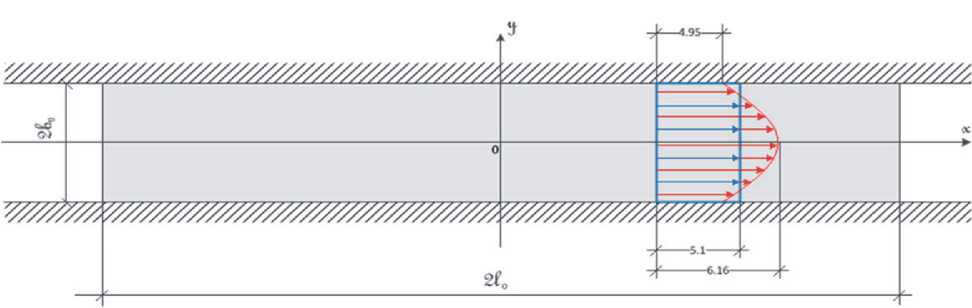
Рисунок 5. Распределение перемещений по ширине срединной плоскости образца: прямолинейный фронт - модель «идеальной жидкости»; криволинейный фронт - данные эксперимента

Заключение. Течение образцов происходит ожидаемо - по прямым линиям тока, параллельным длинной стороне прямоугольника. Продольные перемещения вблизи неподвижных стенок заметно отстают от перемещений вдали от границы, а максимальные перемещения наблюдаются на оси симметрии образца. Этот факт говорит о наличии ненулевых касательных напряжений и скоростей угловых деформаций в рассматриваемых течениях тонкого пластического слоя. При сравнении результатов экспериментов с точным решением краевой задачи в рамках математической модели «идеальной жидкости» выявлено, что они находятся в противоречии. Корректное описание течения удается выполнить только в рамках общей математической модели «вязкой жидкости», при условии осреднения по толщине рассматриваемого пластического слоя.