Моделирование и визуализация процессов формирования и развития инновационных кластеров

Основным методологическим ограничением объективности исследования процессов кластеризации экономического пространства, является наличие в границах исследуемой территории областей, не покрытых точками измерения значений исследуемых показателей кластерного развития. Получение количественной оценки исследуемых экономических показателей кластерного развития в точке пространства X, в которой не проводились измерения, на основе имеющегося набора количественных данных для других точек пространства происходит на основе интерполяции имеющихся значений. Необходимо отметить, что интерполяция процессов социально-экономического развития территорий на сегодняшний день не получила широкого теоретического осмысления в российской научной литературе.

С точки зрения теории и методологии геостатистики анализ процессов кластеризации экономического пространства базируется на определении географических границ и координатной привязки территории, в рамках которой проведены измерения значений выбранной экономической величины Z. Объективно сложившая под действием комплекса различных факторов структура размещения предприятий и организаций-участников инновационных кластеров переделяет неравномерный произвольный характер распределения на территории набора точек, для которых получены значения выбранной величины Z.

В ходе исследования уточнено определение «сети мониторинга данных» применительно к задаче пространственного моделирования процессов формирования и развития инновационных кластеров. Соответственно, «сеть мониторинга процессов кластеризации экономического пространства» представляет собой произвольно распределённый на исследуемой территории набор точек наблюдения, имеющих координатную привязку (x,y), для которых получены значения экономических показателей кластерного развития. Традиционный геостатистический подход к построению сети мониторинга данных и формулировке задачи пространственного оценивания заданной точки x представлен на рисунке 1 [2]. Необходимо отметить, что с точки зрения геостатистического анализа сеть мониторинга может включать в себя имеющие как непрерывные, так и строго дискретные значения пространственные переменные. Дискретные переменные применительно к анализу эффективности реализации кластерной политики для территории могут также иметь качественный характер. Примерами непрерывных пере- менных, характеризующих процессы экономического развития, являются: рентабельность предприятий-участников кластера, производительность труда, удельный вес инновационной продукции и т.д.

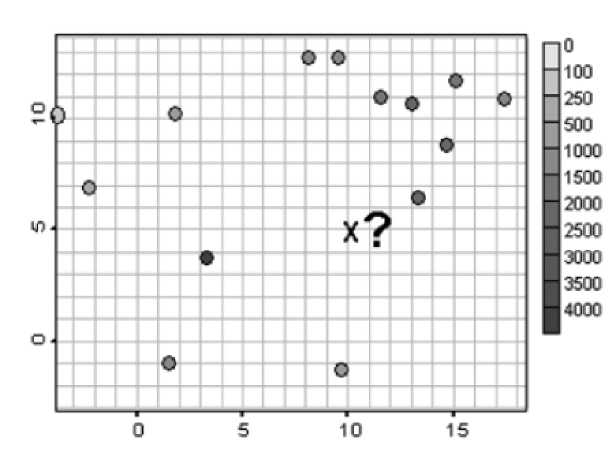
Рис. 1. Построение сети мониторинга данных и формулировка задачи пространственного оценивания заданной точки x

Источник: В. В. Демьянов, Е. А. Савельева. Геостатистика: теория и практика

Примерами дискретных переменных, характеризующих процессы экономического развития, являются: среднесписочная численность работников организаций (человек), количество созданных (используемых) передовых технологий (единиц). Примерами качественных дискретных переменных, характеризующих эффективность кластерной политики экономического развития, являются: уровень развития инновационной инфраструктуры, степень экономической интеграции с другими участниками кластера и т.п.

Следовательно, необходимым условием для применения методологического инструментария геостатистики к задаче моделирования инновационных кластеров является определение системы координат для области Z ( x ), которая задаётся всеми включёнными в область анализа переменными [1, 3, 4]. В общем виде координатная привязка, являющихся объектом геостати-стического анализа регионализованных переменных может быть трёх следующих типов:

• 1.    Пространственная привязка. Данный тип координатной привязки определяет пространственное положение точек измерения анализируемых переменных. Местоположение точек привязывается непосредственно к географическим координатам либо рассматривается относительно заранее выбранных стационарных объектов. Второй подход является достаточно специфичным и не рассматривается как актуальный для задач моделирования процессов формирования и развития инновационных кластеров.

• 2.    Временная привязка. Данный тип привязки содержит данные о времени проведения измерений исследуемых переменных, при этом сами данные о времени проведения измерений также могут иметь как абсолютное, так и относительное исчисление.

• 3.    Пространственно-временная привязка. Данный тип привязки одновременно содержит данные о пространственном положении и времени проведения измерений анализируемых переменных [2].

Итоги. Определено, что в рамках пространственного моделирования процессов формирования и развития инновационных кластеров временной фактор не имеет принципиальной роли. Это обусловлено самим характером кластерного развития, так как кластерная политика реализуется в долгосрочном периоде и в качестве наиболее удобного временного периода отчётного обычно применяется календарный год. Таким образом, для решения практических задач анализ динамики развития кластеров может быть дискретным во времени, и основываться на первом пространственном типе.

Следовательно, основным требованием к координатной системе сети мониторинга процессов кластеризации экономического пространства территории российских регионов является метричность. Моделирование процессов формирования и развития инновационных кластеров должно сопровождаться определением геостатистиче-ской метрики, позволяющей вычислять расстояние между местоположением предприятий и организаций кластера. Для задач геостатистического анализа процессов кластерного развития предлагается ис- странства R2, обладающего такой метрикой, что расстояние между двумя точками пространства X1 = (x1, y1) и X2 = (x2, y2) определяется евклидовой нормой:

||⁽X i ,y i ⁾⁽x 2 ,У г )0 = VUi - x₂)² + (У 1 - y₂⁾²

При этом сеть мониторинга называется «кластерной» если имеет сегменты с существенно высокой плотностью точек измерений исследуемых величин, по сравнению со всей остальной областью наблюдений. Если выявленные сегменты с повышенной плотностью измерений в свою очередь характеризуются более высокими или низкими значениями исследуемой величины, возникает необходимость в проведении процедуры декластеризации с целью получения репрезентативной статистики и исключение ошибок в средних значениях, вариаций и т.д. Таким образом, методологический инструментарий геостатистики как междисциплинарного направления в высокой степени комплементарен кластеру как экономической категории и может применятся с целью развития концептуальных основ пространственного моделирования кластеров.

пользование двумерного евклидового про-