Моделирование импульсного нагружения подводного трубопровода, заполненного жидкостью

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

Современные подводные трубопроводы часто имеют двухслойные оболочки в виде стальной трубы (СТ) и бетонного покрытия (БП), стабилизирующие его вблизи жесткого дна. В работах [1–5] проводились исследования воздействия импульсных нагрузок на элементы подводных конструкций. В данной статье рассматривается задача воздействия ударных волн на участок подводного трубопровода, заполненного внутренней жидкостью, в результате инициации внешнего импульсного возмущения. При использовании классических уравнений динамики сплошных сред выполнялось моделирование на разработанном авторском пакете программ [6; 7] с использованием подходов к моделированию из [8]. Постановка решаемой задачи имеет схожие начальные условия из работы [5] с важным дополнением – рассматриваемый подводный трубопровод, заполнен внутренней жидкостью. Учет пластических деформаций производится в соответствии с [9–12]. Из [13] для воды используется уравнение состояния в форме Тета. Для предложенной ранее методики решения нелинейных динамических задач гидрогазодинамики из [8] при численном решении уравнений применяется модификация схемы Годунова повышенной точности [14; 15]. В работах [16–20] модификация численной схемы из [14; 15] едина для газодинамических и для упругопластических задач. Теоретические материалы и обобщающие экспериментальные данные по взрывным процессам и свойствам материалов при взрывных нагружениях содержатся в работах [21–26]. В отличие от приведенных результатов расчетов, выполненных на других кодах [27–30], связанных с различными оболочечными конструкциями, подверженными подводным взрывам, в текущей работе для выделения и сопровождения контактной поверхности используется точное решение задачи распада разрыва, рассчитываемое в локальных сетках.

Разработанность темы

Существует три основных подхода решения задач математического моделирования импульсного взаимодействия элементов конструкций с жидкостью: это метод характеристик, методы конечных разностей и метод конечных объемов. Подробное описание упомянутых методов дано в обзорах П.И. Чушкина и Л.В. Шуршалова и В.Н. Охитина [31; 32]. Метод характеристик, несмотря на высокую эффективность исследований структуры ударных волн, слабо применим для реальных задач из-за своей громоздкости, он подходит в большей степени для одномерных течений [33, с. 264, 292]. Для корректной применимости чисто лагранжевых подходов требуется постоянная перестройка расчетных сеток [12; 34]. В то же время для моделирования высокоскоростных процессов развитие получили конечно-разностные схемы, использующие совместные лагранжево-эйлеровы подходы без привязки линий расчетной сетки к границам раздела контактирующих сред. Это схемы В.Ф. Ноха [33 с. 128],

Ф.Х. Харлоу [33, с. 316], метод «крупных частиц» О.М. Белоцерковского [35] и метод для течений неоднородной среды, предложенный С.М. Бахрахом, В.Ф. Спиридоновым, А.А. Шаниным [36]. Кроме них, являясь различными модификациями схемы С.К. Годунова [37], для решения взрывных задач получили распространение методы конечного объема FVM (finite volume methods), сочетающие возможности лагранжево-эйлеровых подходов [38]. К слабой стороне программных кодов на базе разностных схем относится первый порядок аппроксимации и обязательное введение искусственной вязкости в области ударных волн [36].

Наиболее широкое распространение для расчета импульсных процессов получила конечно-разностная схема С.К. Годунова и ее многочисленные модификации [37]. Оригинальная схема С.К. Годунова основана на точном решении задачи распада разрыва, монотонна и допускает использование лагранжевых, лагранжево-эйлеровых и эйлеровых подходов при моделировании быстропротекающих высокоскоростных процессов. Использование решения задачи распада разрыва дает возможность выделять ударные фронты и контактные разрывы, привязав к ним расчетные сетки. Данная разновидность конечно-разностных схем была расширена на моделирование различных физических процессов и выделена в отдельный класс схем конечного объема (FVM). Но из-за первого порядка аппроксимации в оригинальной схеме Годунова имеет место нерегулируемая схемная вязкость, что является очевидным недостатком. Распределение параметров в расчетных ячейках в оригинальной схеме Годунова кусочно-постоянное. Для задач высокоскоростного нагружения достаточно распространены модификации схемы Годунова, которые используют разные способы распределения параметров, в основном добавляются дополнительные ячейки, тем самым увеличивается расчетный шаблон, что позволяет редактировать параметры на границе расчетной ячейки, участвующей в задаче распада разрыва. В некоторых известных пакетах программ для задач импульсного нагружения используется схема Ван Лира [39], но работа с данной модификацией ощутимо затруднена из-за проблем при использовании неструктурированных разностных сеток и реализации граничных условий, так как в трехмерном случае дополненный разностный шаблон приобретает вид 5*5*5.

В трудах [40; 41] был предложен монотонный в области разрывных решений, допускающий использование лагранжевых и лагранжево-эйлеровых подходов метод повышения точности схемы С.К. Годунова, без увеличения стандартного разностного шаблона 3*3*3. Повышение аппроксимации до второго порядка достигается на неувеличенном шаблоне за счет сближения областей влияния разностной и дифференциальной задач на неравномерной подвижной сетке, включая границу расчетной области. При подготовке параметров для решения задачи распада разрыва необходимы изменения только на шаге предиктор. Однако для достижения монотон- ности на разрывных решениях на шаге предиктор осуществляется переход к задаче распада разрыва оригинальной схемы Годунова первого порядка. Данная методика реализована в разработанном авторском коде и применяется для решения нижеописанной задачи.

Постановка задачи

Рассматривался участок трубопровода (рис. 1), начало координат находится на оси Z в середине трубы, внешний радиус R = 58,85 см, внутренние диаметр и толщина стальной трубы соответственно 115 и 2,7 см, толщина бетонного покрытия (БП) 10 см, параметры взяты из [5]. Предполагается, что нижняя часть трубопровода находится над жестким дном на высоте 19,8 см (ось трубопровода проходит на высоте 90 cм от дна). Центр области инициации импульсного возмущения находится на высоте 65 см от жесткого дна, диаметром 0,5 м и массой 123 кг, при этом расположен на расстоянии 130 см от центра трубопровода. Размеры расчетной области 290×200×600 см, длина подводного трубопровода 6 м. На внешних границах расчетной области поставлены искусственные условия продолжения потока [8]. Эти условия выполняются присвоением граничным значениям параметров потоков из внутренних ячеек. Давление во всех средах и внутри трубопровода в начальный момент времени полагалось равным 0,1 МПа.

Рис. 1. Фрагмент расчетной области

Fig. 1. Fragment of the calculation area

На рис. 1 изображен фрагмент расчетной области, решаемой задачи, включая оболочки подводного трубопровода, область начальной инициации импульсного возмущения, поверхность жесткого дна, а также внешнюю (для лучшей визуализации на схеме расчетной области не выделена) и внутреннюю жидкость подводного трубопровода.

На рис. 2 приведены поверхностные сетки с размером ячеек регулярной сетки для деформируемой стальной стенки 0,5 см, для бетонного покрытия – 2 см, для внутренней и внешней жидкости – 3 см, для начальной области инициации импульсного возмущения – 2 см. В расчете использовалось порядка 14,5 млн ячеек.

Данная сетка была выбрана после проведения предварительных расчетов при оценке влияния действий прямых, преломленных и отраженных ударных волн на подводный трубопровод, заполненный жидкостью. Характеристики подводного трубопровода взяты из [5]. Для описания процессов в плотных сжимаемых средах (сталь, бетон) применяется баротропное уравнение состояния (УРС) вида p = p (р), связывающее давление p и плотность среды р , позволяющее избежать интегрирования уравнения сохранения энергии. Критерием перехода из упругого напряженно-деформированного состояния в пластическое является условие текучести Мизеса: J ₂ = = 0,5 S ij S ij >  (1/3) о Т ² , где J 2 - второй инвариант девиатора тензора напряжений S j , с _Т - предел текучести. Для описания процессов упругопластического деформирования сред применяется теория пластического течения Прандтля — Рейса. Для контактируемых твердых тел предполагается идеальная пластичность. Для жидкости используется уравнение состояния в форме Тета

Р + Bq    c₀ 2

£ =-----⁰---0—, где £ - внутренняя энергия единицы

(у- 1)Р У-1

массы, у - показатель адиабаты, В 0 , с 0 - некоторые константы, В 0 = 304,5 МПа, с 0 = 1450 м/c. Из [5] для внутренней и внешней жидкости принято γ = 7,15.

Рис. 2. Поверхностные сетки

Fig. 2. Surface grids

Зависимость показателя адиабаты у от р для про- дуктов детонации принимается в виде:

у⁽р ) =

р о /р R , A exp ( - R ₁ р ₀ /р ) + R ₂ р ₀ /р B exp ( - R ₂ р ₀ /р ) + C ( 1 + ю )( р/р ₀ ) ^{1 +}“

A exp ( - R ] р ₀ /р ) + B exp ( - R ₂ р ₀ /р ) + C ( р/р ₀ ) ^{1 +}“

,

полученной с использованием УРС идеального газа и УРС типа JWL.

Расчеты проводились до времени 1,6 мс на вычислительной машине i9-13900K на 24 ядрах, что соответствует завершению действия основной импульсной нагрузки. Расчет импульсного нагружения и реакции подводного трубопровода, заполненного жидкостью, в течение 1,6 мс занял 53 ч физического времени. Возмущение, вызванное ударной волной, распространяется по расчетной области и поочередно нагружает бетонное покрытие, стальную стенку, после чего оно переходит на внутреннюю жидкость подводного трубопровода, а также отражается от жесткого дна, и воздействие продолжается. Наблюдается сложная нелинейная трехмерная картина взаимодействия волн.

На рис. 3 в сечении Z =0 в моменты времени 0,51; 0,73; и 1,23 мс показано движение ударной волны от области инициации импульсного нагружения и ее распространение по внешней жидкости до взаимодействия с деформируемыми стенками подводного трубопровода и далее движение по заполненной жидкостью внутренней полости трубопровода, как поперёк, так и вдоль него. Здесь и далее визуализация распределения давлений в каждой подобласти выбрана в разных масштабах для лучшего отображения. Красным цветом отмечены области более высокого давления, синим – области низкого давления. Наблюдается отражение ударной волны от жесткого дна и ее последующее распространение по расчетной области, включая область подводного трубопровода. К моменту времени 1,23 мс размер области, занятой газообразными продуктами взрыва, существенно увеличивается, область становится соизмеримой с размером сечения подводного трубопровода.

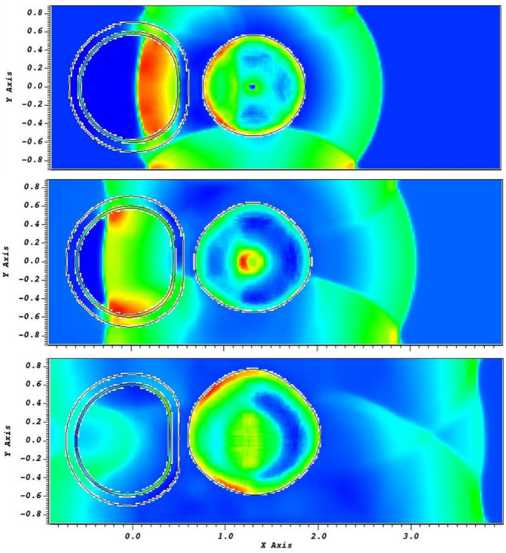
Рис. 3. Взаимодействие ударной волны с конструкцией подводного трубопровода, заполненного жидкостью, в центральном сечении Z =0 в моменты времени: 0,51; 0,73; 1,23 мс

Fig. 3. Interaction of a shock wave with the structure of an underwater pipeline filled with liquid in the central section Z =0 at the moments of time: 0.51; 0.73; 1.23 ms

На рис. 4 в поперечном сечении Y=0 в моменты времени 0,278; 0,904; 1,413 мс отображены этапы поперечного распространения ударной волны по внешней жидкости, по подводному трубопроводу и далее по внутренней полости трубопровода, заполненной жидкостью. Наблюдается отражение ударной волны от противоположной стенки трубопровода к моменту времени 0,904 мс и далее движение отраженной волны вдоль трубопровода.

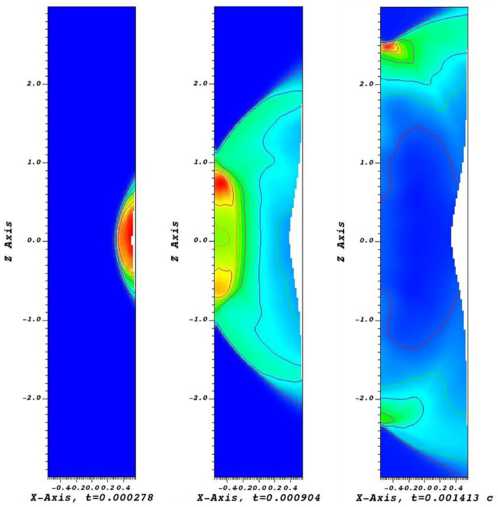
Рис. 4. Взаимодействие ударной волны с конструкцией подводного трубопровода, заполненного жидкостью, в сечении по длине трубопровода ( Y =0) в моменты времени: 0,278; 0,904; 1,413 мс

Fig. 4. Interaction of a shock wave with the structure of an underwater pipeline filled with liquid in the cross-section along the length of the pipeline ( Y =0) at the moments of time: 0.278;

0.904; 1.413 ms

На рис. 5 показаны зависимости скорости по оси Х от времени для двух состояний подводного трубопровода – с внутренней жидкостью и без нее. Стоит отметить характерное поведение скорости в период времени с 0,7 до 0,9 мс, вызванное противодействием внутренней жидкости внешнему возмущению. В то же время максимальные значения скорости близки для трубопровода без внутренней жидкости и с ней.

На рис. 6 показана зависимость давления от времени в точке ближайшей к области инициации импульсного возмущения на внутренней поверхности трубопровода с внутренней жидкостью, а также показана зависимость давления от времени в точке ближайшей к области инициации импульсного возмущения на внешней поверхности трубопровода: кривая ( 2 ) с внутренней жидкостью, кривая ( 3 ) для трубопровода без внутренней жидкости.

На рис. 7 приведены формы подводных трубопроводов с внутренней жидкостью и без нее в момент времени 1,52 мс. Наблюдаются заметно большие перемещения в трубопроводе без внутренней жидкости, нежели в трубопроводе с внутренней жидкостью, что подтверждает график на рис. 8.

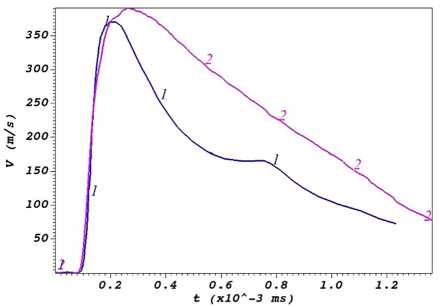
Рис. 5. Зависимости скорости по оси X от времени на внешней стенке подводного трубопровода в точке ближайшей к области инициации импульсного возмущения: 1 – трубопровод с внутренней жидкостью; 2 – без внутренней жидкости

Fig. 5. Dependences of the velocity along the X axis on time on the outer wall of the underwater pipeline at the point closest to the region of initiation of the pulse disturbance: 1 – pipeline with internal liquid; 2 – without internal liquid

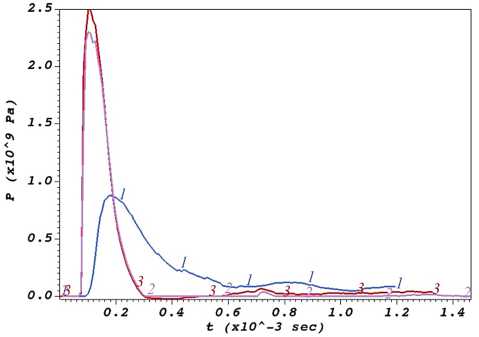
Рис. 6. Зависимость давления от времени для трубопровода, заполненного внутренней жидкостью: на внутренней поверхности стенки трубопровода ( 1 ); на внешней поверхности стенки трубопровода для двух случаев – с внутренней жидкостью ( 2 ) и без нее ( 3 )

Fig. 6. Pressure versus time for a pipeline filled with internal liquid: on the internal surface of the pipeline wall ( 1 ); on the external surface of the pipeline wall for two cases – with internal liquid ( 2 ) and without it ( 3 )

Рисунки 9, 10 иллюстрируют влияние жесткого дна на внешние нагрузки и на скорости движения по трубопроводу.

Заключение

Приведено решение трехмерной задачи нелинейного взаимодействия подводного трубопровода, содержащего внутреннюю жидкость, с ударными волнами в окружающей жидкости от внешнего импульсного возмущения.

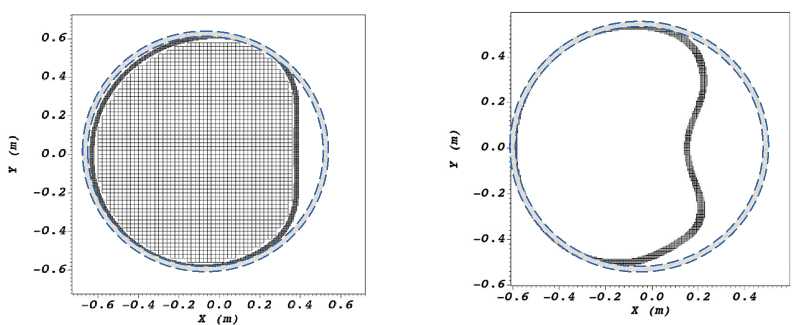
а

b

Рис. 7. Форма поперечного сечения ( Z =0) подводного трубопровода при t =1,52 мс: а – для трубопровода с внутренней жидкостью; b – для трубопровода без внутренней жидкости

Fig. 7. The cross-sectional shape ( Z =0) of an underwater pipeline at t =1.52 ms: a – for a pipeline with internal liquid; b – for a pipeline without internal liquid

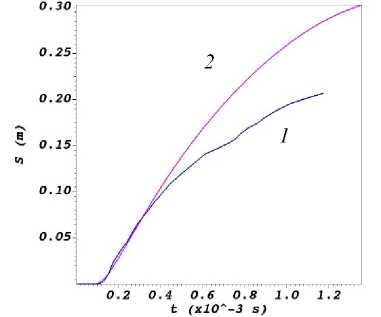
Рис. 8 Перемещения лобовой точки стенки подводного трубопровода в зависимости от времени: 1 – трубопровод с внутренней жидкостью; 2 – без внутренней жидкости

Fig. 8. Displacements of the frontal point of the wall of an underwater pipeline depending on time: 1 – pipeline with internal liquid; 2 – without internal liquid

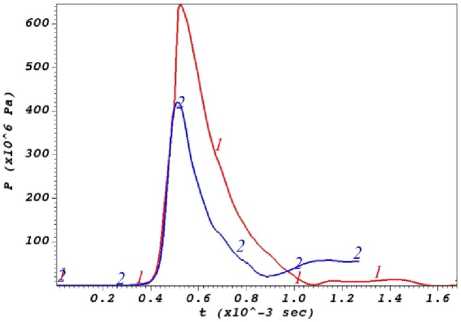
Рис. 9. Влияние дна. Давление со стороны внешней жидкости: 1 – нижняя точка трубопровода, 2 – верхняя точка трубопровода

Fig. 9. Effect of the bottom. Pressure from the external liquid:

1 – lower point of the pipeline, 2 – upper point of the pipeline

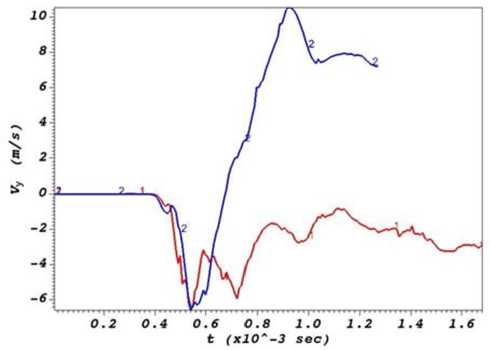
Рис. 10. Влияние дна. Скорости по оси Y со стороны внешней жидкости: 1 – нижняя точка трубы, 2 – верхняя точка трубы

Fig. 10. Effect of the bottom. Velocities along the Y axis from the external liquid side: 1 – lower point of the pipe, 2 – upper point of the pipe

Внутренняя жидкость снижает уровень внешних нагрузок и уменьшает формоизменение конструкции подводного трубопровода. Это связано с демпфирующим эффектом внутренней жидкости подводного трубопровода. В результате внутренняя жидкость не только снижает локальные напряжения, но и минимизирует риск разрушения стенок подводного трубопровода, это указывает на важность учета ее влияния при проектировании подводных трубопроводов.

Проанализировано влияние донной поверхности на поведение трубопровода с жидкостью при импульсной нагрузке. Наблюдается перераспределение всех параметров взаимодействия: давления на стенки подводного трубопровода, его скорости движения и перемещений