Моделирование изменения остаточной циклической деформации ниток в режиме периодического растяжения

ОБУВНЫЕ НИТКИ, ОСТАТОЧНАЯ ЦИКЛИЧЕСКАЯ ДЕФОРМАЦИЯ, МОДЕЛИРОВАНИЕ, АНАЛИЗ РАЗМЕРНОСТЕЙ, НЕЛИНЕЙНЫЕ СВОЙСТВА НИТКИ, ЭФФЕКТ УПРОЧНЕНИЯ НИТКИ

В работе исследовано влияние на деформационное состояние швейных ниток эксплуатационных и технологических факторов. В качестве факторов использованы такие характеристики, как удельная работа растяжения ниток при затяжке обуви, время и скорость нагружения. Мерой соотношения напряжений и деформаций, возникающих в нитке первоначально при затяжке швов и в дальнейшем в процессе эксплуатации изделий, являлась остаточная деформация. Этим показателем оценивалось деформационно-напряженное состояние швейных ниток.

На основе результатов проведенных исследований выполнено моделирование остаточной циклической деформации с применением теории размерностей. Построена модель зависимости остаточной циклической деформации от эксплуатационных и технологических факторов. Данная модель может использоваться в задачах прогнозирования долговечности обуви, изготовленной с применением ниточных соединений.

SHOE THREAD, RESIDUAL CYCLICAL DEFORMATION, MODELING, DIMENSION ANALYSIS, NONLINEAR PROPERTY OF THREADS, HARDENING EFFECT OF THREADS

The influence of exploitation and technological factors on deformation state of sewing threads is investigated in this article. The following characteristics are used as the factors: work of thread extension during footwear lasting, time and speed of loading. Residual deformation is used as a measure of correlation between strain and deformation which first occurs in the thread during stitch lasting and during product exploitation further on. This measure is also used to estimate the deformation and strain state of sewing threads.

On the base of the research results the simulation test of residual cyclic deformation with the use of dimension theory was fulfilled. The model of dependence of residual cyclic deformation on exploitation and technological factors is developed. This model can be used in the problems of footwear durability prediction made with the use of sewing thread junction.

Основным методом скрепления деталей верха обуви является ниточный. В настоящее время для предприятий обувной отрасли остро не стоит вопрос о прочности швейных ниток, так как в производстве широко применяются синтетические швейные нитки, обладающие достаточно высокой прочностью. Однако актуальной остается проблема их растяжения в ниточном шве в процессе эксплуатации обуви.

Вследствие особенностей строения полимерных материалов, к которым в частности относятся и швейные нитки, для них характерно наличие трех слагающих частей деформации;

наряду с небольшой истинно упругой деформацией большую долю обратимой деформации в этих материалах составляет эластическая, медленно развивающаяся и исчезающая. Кроме того, одновременно развивается и остаточная необратимая деформация. С одной стороны, она зависит от физико-механических свойств применяемых ниток, а с другой – от режима эксплуатации изделий [1]. С достаточным основанием остаточную деформацию можно рассматривать как меру соотношения напряжений и деформаций, возникающих в нитке первоначально при затяжке швов и в дальнейшем в процессе эксплуатации изделий. В известных работах этому вопросу уделено недостаточное внимание, поэтому одной из причин является сложность объекта исследования. Однако он имеет существенное практическое значение в отношении как производства изделий,так и прогнозирования их эксплуатационных характеристик.

По мере многократного растяжения в нитях изменяется расположение отдельных частей волокон или элементарных нитей, недостаточно зажатых при скручивании. В результате структурные элементы располагаются более ориентированно вдоль продольной оси волокон (или нитей), лучше взаимодействуют друг с другом за счет межмолекулярных связей, сил трения и так далее. Эти явления сопровождаются увеличением остаточных удлинений, состоящих в основном из необратимой пластической, а также из медленно исчезающей части эластической деформации. В последующих циклах быстрое нарастание удлинений резко замедляется, структура нити в известной мере стабилизируется.

Разрушение структуры идет слабо и не может вызвать сколько-нибудь существенного ухудшения механических свойств. Если структура волокон или нитей хорошая, а величина и частоты растяжений таковы, что они вызывают только быстрообратимые деформации, состоящие в основном из упругих и отчасти из быстро релаксирующих эластических компонентов (то есть из таких, которые в каждом цикле растяжения успевают исчезнуть за время разгрузки и отдыха), в результате воздействий не происходит существенных ухудшений структуры материала и в итоге она остается почти неизменной.

Материал выдерживает очень большое число растяжений, нередко определяемое десятками и сотнями тысяч, а иногда и миллионами циклов. Развитие структурных дефектов и накопление необратимых деформаций, состоящих из медленных эластических и пластической частей, идет очень медленными темпами; лишь после большого числа циклов накапливается некоторая необратимая деформация [2].

В проведенном исследовании ставилась задача моделирования остаточной циклической деформации ниток как величины, определяемой физико-механическими свойствами ниток и характеристиками режима их периодического рас- тяжения в соединительных швах деталей обуви с использованием анализа размерностей, который хорошо зарекомендовал себя в научных исследованиях в целом ряде областей.

За показатель изменения напряженно-деформированного (в дальнейшем НД) состояния нитки можно принять нарастающую во времени величину остаточной циклической деформации ∆l_оц, являющуюся следствием периодического нагружения нитки в шве в процессе эксплуатации и развития в ней необратимой, пластической составляющей полной деформации. Исходное НД состояние нитки задается на стадии производства изделия. Оно обусловлено работой, совершённой при затяжке соединительного шва. Эта работа определяет начальную внутреннюю энергию деформации нитки в этом шве. Количественной мерой ее логично принять удельную энергию деформации нитки, то есть удельную работу растяжения нитки при затяжке соединительного шва r. На стадии эксплуатации нитка в шве подвергается периодическому с частотой ю влиянию сторонних факторов, «расшатывающих» структуру нитки и уменьшающих внутреннюю энергию деформации нитки и, тем самым, снижающих прочность соединительного шва. Снижение внутренней энергии деформации нитки в шве происходит и во времени t вследствие релаксационных процессов. Таким образом, в проведенном исследовании НД состояние нитки описывалось функцией

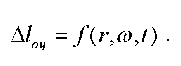
Для ответа на вопрос о возможности существования такой функции проведем анализ размерностей введенной формы (1).

Представим выражение (1) в виде, содержащем лишь комбинации исходных величин. Для этого используем релеевский метод решения размерных систем [3]. Выразим вначале размерности исходных величин,то есть величин, входящих в (1).

Используя систему СИ, введем буквенные обозначения размерностей основных единиц в системе СИ: единица массы — М; единица длины — L; единица времени — θ. С помощью них построим так называемые формулы размерно- стей для рассматриваемых величин: ∆lоц, r, ω, t. С этой целью в выражении, определяющем размерность каждой величины, принятые обозначения основных единиц заменяем введенными символами. В результате получаем формулы размерностей величин формы (1). Эти формулы представлены в таблице 1.

Очевидно, что выражение (1) являетcя лишь общей формой записи зависимости между введенными величинами. В действительности характер влияния аргументов на функцию, вообще говоря, неодинаков. Поэтому естественно с точки зрения приближения к истинной зависимости следует использовать такую формулу:

M„_l=f(.r\<_B^b,t-> ,     (2)

где а, b, с — некоторые безразмерные показатели степеней, отражающие характер влияния факторов r, ω, t на величину ∆lоц.

Формула (2) является отправной (исходной) при проведении анализа размерностей названным выше методом. Далее действуем следующим образом.

Подставим в (2) вместо обозначений величин формулы их размерностей из таблицы 1. Имеем:

L^q^^l^f^ . (3)

Для того чтобы последнее соотношение было однородным относительно размерностей, должны выполняться следующие отношения между показателями степеней:

для L: 1 = 2 a ;

для Θ : 0 = – 2 a – b + c.

Из этих соотношений имеем: a = 0,5; и c = 1 + + b. Подставим найденные значения в форму (2):

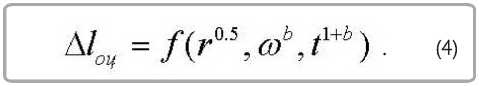
Объединяя величины, имеющие одинаковые показатели степеней, получим две комбинации:

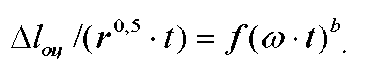
Обе они оказались безразмерными. Это свидетельствует о том, что уравнение, соответствующее форме (1), существует, то есть имеются основания считать полной исходную группу величин, представленную этой формой. Таким образом, четыре исходных величины удалось объединить в две безразмерные комбинации. В соотношении (5) неизвестным остается вид функции f и значение показателя степени "b" .

Для поиска подходящей аппроксимации (5) перепишем его в следующем виде:

^оц ^^♦/♦[/(бУ/У’], (6)

где A – некоторый безразмерный согласующий (масштабный) коэффициент.

Принимая во внимание, что величину t можно представить как t = n/ω, где n – число циклов нагружения, окончательный вид математической модели формы (1) станет таким:

^ = (^-r°'5)-K-[/W]. (7)

Учитывая, что удельная работа разрыва r , характеризующая неизменные для данной нити ее механические свойства, является постоянной величиной, а ω = Const по методическим соображениям, и чтобы отчетливо уви-

Таблица 1 – Величины, входящие в форму (1), их размерности и формулы размерностей
Обозначение величины	Размерность в системе СИ	Формула размерности
∆lоц	м	L
r	Н м/кг	L2 Θ-2
ω	с -1	Θ -1
к           t	с	Θ ---------J

деть важную особенность построенной модели, формально соотношение (7) представим так:

,           (8)

где:

. (9)

Функцию (8) с полным основанием можно определить как квазилинейную, так как формально величину K(n) можно рассматривать в качестве углового коэффициента прямой, описываемой линейной функцией ∆l_оц = Kn при K = Const. Но, как следует из (8), K = K(n ), и эта зависимость отображает влияние на остаточную циклическую деформацию ∆l_оц процесса релаксации деформации, обусловленной наличием релаксационных свойств нити. Следовательно, по мере роста величины n график функции ∆l_оц = [K(n)]n будет все больше отклоняться от прямой ∆L_оц = Kn. Эта важная особенность построенной модели может рассматриваться как один из сильных критериев качественного соответствия соотношения (8) модели изучаемой зависимости.

Для поиска подходящей конкретной модели зависимости (8) был проведен эксперимент на нитках 70Л и 80Л с целью изучения однофакторной зависимости ∆lоц = φ(n). Исследования были проведены на пульсаторе ПН-5 при частоте нагружений го = 300 мин1, статической нагрузке Рт = 1,5 Н и величине циклической деформации ∆lц, равной 10 мм.

Выбранные значения частоты соответствовало средней скорости ходьбы, а значение статической нагрузки – среднему усилию, возникшему при затяжке соединительного шва [4, 5]. При выборе циклической деформации учитывались соображения, изложенные в [4].

Как количественная мера остаточной циклической деформации использовалось необратимое нарастающее удлинение ∆l испытываемой нитки, выраженное в мм. График зависимости ∆l = f(n) , где n – число циклов нагружения, представлен на рисунке 1.

Полученный график показывает, что до значения n = 60 функция ∆l = f(n ) ведет себя как линейная. Однако после этой точки график начинает все больше отклоняться вниз от прямой, отображая тем самым растущее влияние на нарастающую остаточную циклическую деформацию процесса релаксации. Как следует из графиков на рисунке 1, начиная от значения n = 60, с ростом n величина К уменьшается. При значении n = 100 значение К становится равным нулю с точностью до ошибки аппроксимации экспериментальных кривых, и в дальнейшем в области n >100 не отклоняется от нулевого значения, то есть наклонный участок кривой переходит в горизонтальный.

Таким образом, нарастание остаточной цик-

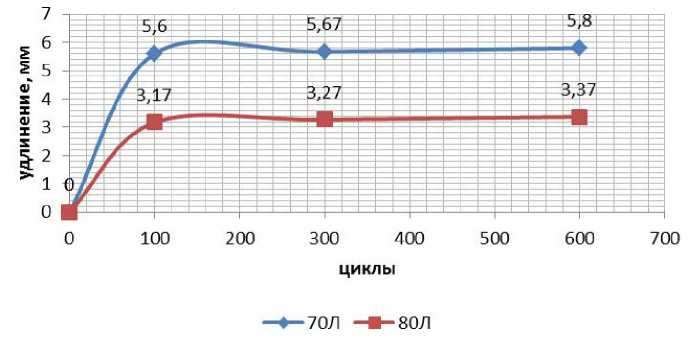
Рисунок 1 – График зависимости остаточной циклической деформации от числа циклов нагружения

лической деформации описывается лишь той частью кривых на рисунке 1, которая лежит в области 0 <  n < 100. Для получения расчетных оценок величины остаточной циклической деформации в конце этой области построена математическая модель в виде степенной функции вида y = ax^{b .} Для этих функций характерно наличие практически линейного участка на достаточно большом удалении от нулевой точки, что соответствует особенностям формы эмпирических кривых на рисунке 1.

С использованием метода наименьших квадратов получены следующие математические модели зависимости (8): для швейной нитки 70Л: Мм = 0,095 n 0,9 ; для швейной нитки 80Л: А l_M = 0,054 n ^0,9. Адекватность моделей оценивалась величиной относительной ошибки аппроксимаций δ (%), определявшейся по формуле δ = (| А 1_Э - А 1_Ж1 / А l) • 100 %, где А 1_э - экспериментальные значения удлинений и А 1_м - соответствующие значения удлинений, вычисленные по уравнениям построенных моделей. Результаты сравнительного анализа величин удлинений представлены в таблице 2.

Для швейной нитки 70Л средняя относительная ошибка аппроксимации δ_ср = 4,1 %.

Для швейной нитки 80Л эта ошибка составляет величину δ_ср = 2,1 %.

Таким образом, получены достаточно точные статистические аппроксимации изученных зависимостей, хорошо отражающие нарастание остаточной циклической деформации швейных ниток в режиме их периодического растяжения.

Особый интерес представляют горизонтальные участки на кривых, изображенных на рисунке 1. Они свидетельствуют о том, что после значения n = 100 не наблюдается нарастания остаточной циклической деформации. Это можно объяснить известным из [6] эффектом упрочнения нити за счет ее предварительного вытягивания. Кривые на рисунке 1 показывают, что после значения n = 100 произошло резкое перераспределение составляющих полной деформации ниток. Иными словами, физико-механические свойства ниток после 100 циклов вытягивания стали существенно другими. Значительно возросла доля упругой деформации, что и объясняет отсутствие остаточной циклической деформации, по меньшей мере, до значения n = 600. Как доказано в ряде исследований, например, в [6], упрочнение нити в ходе предварительного вытягивания связано с распрямлением и переориентацией макромолекул полимера. Этот эффект, с одной стороны, позволяет несколько иначе рассматривать физические механизмы, обусловливающие долговечность ниточных соединений деталей обуви. С другой стороны, он наводит на мысль о дополнительных операциях по подготовке ниток к использованию в технологическом процессе производства обувных изделий, в частности, предварительное вытягивание ниток.

Таким образом, проведенное исследование показало, что нитка при циклическом нагружении ведет себя как сложная нелинейная система. Процесс такого нагружения включает три стадии: линейное нарастание остаточной циклической деформации, нелинейное ее снижение и, наконец, упрочнение нитки и изменение остаточной циклической деформации. Полученные результаты могут быть использованы для дальнейших исследований надежности ниточных соединений деталей обуви.

Таблица 2 – Экспериментальные значения ∆lэ и значения ∆lм , полученные с помощью моделей
Число циклов N	Для швейной нитки 70Л			Для швейной нитки 80Л
	∆lэ (мм)	∆lм(мм)	δ (%)	∆lэ (мм)	∆lм(мм)	δ (%)
20	0,8	0,8	0,0	1,4	1,4	0,0
40	1,6	1,5	6,2	2,6	2,6	0,0
60	2,4	2,2	8,3	4,0	3,8	5,0
80	2,8	2,8	0,0	5,0	4,9	2,0
100	3,2	3,4	6,2	5,7	5,9	3,5