Моделирование экономического роста районов Бурятии

Введение и новизна. Моделирование роста экономики является довольно изученной и вместе с тем не теряющей своей актуальности темой исследования. Наличие правильно подобранной модели позволяет в упрощенной форме описать изучаемое явление, оценить параметры равновесия, проверить справедливость выдвигаемых гипотез, выполнить прогноз моделируемой переменной, выделить причинно-следственные связи, объясняющие принципы функционирования изучаемой экономической системы. Получение такой модели задача нетривиальная так как это требует либо наличия теоретико-игровой модели, описывающей изучаемое явление, либо достоверных, подтвержденных опытом сведений о механизме его функционирования.

Одной из ранних теоретических работ, посвященных региональному экономическому росту, является модель Хойта [1]. Основной идеей данной модели является разделение экономики региона на базовый сектор и сектор услуг. Если предположить, что отрасль промышленности может быть источником эконмического 64

роста региона тогда, когда она в состоянии производить продукции больше, чем может быть куплено жителями данного региона, то к базовым могут быть отнесены экспортирующие отрасли региона, а к сфере услуг - все остальные. В этом случае общий доход региона Т_т будет складываться из дохода в базовом секторе Y_b и дохода в секторе услуг Y_s. Доход в секторе услуг растет пропорционально росту общего дохода региона, а доход в базовом секторе зависит от внешнего спроса на экспортируемый товар:

Y t = Y_b + Y_s;

Ys - do + niYT, 0 < d < 1;

Y b = Y_b.

В результате прирост доходов в регионе зависит от прироста доходов в базовом секторе и от того, какими темпами растут доходы в сфере услуг:

V _ ^ao I    ^Yb .

Y T  --1--;

XY l _ ^№ ь    ^Yb

Y_T Y b a o +Yb ■

Ключевую роль в модели играет константа dо: если она равна нулю, то доходы региона растут с такой же скоростью, что и доходы в базовом секторе, что, в свою очередь, предполагает постоянство доли доходов в сфере услуг в общих доходах региона. Если do > 0, то доходы в регионе растут медленнее, чем в базовом секторе; если do < 0 -быстрее, чем в базовом секторе.

Над дальнейшим развитием модели Хойта независимо друг от друга работали Д. Норт, Ш. Тибу и Р. Эндрюс [2]. Их модель построена по принципу кейнсианской модели совокупного спроса. В простейшей версии модели совокупный доход или производство Y равно сумме потребления C и чистого экспорта (экспорт X минус импорт M) . Размер экспорта задается экзогенно, а размер потребления и импорта пропорционален уровню дохода в экономике и зависит от предельной склонности к потреблению и импорту, соответственно:

Y - С + Х- М;

X -Х о ;

С — с Y при 0 < с < 1;

М — rnY при 0 < т < 1.

В результате нескольких преобразований авторы приходят к выражению, показывающему мультипликативный эффект роста экспорта на выпуск в экономике региона, зависящему от предельной склонности потреблять и импортировать:

Х Y - —1—ХХ - ХХ..

1 - (с- т)

Модель показывает, что более быстро развивающиеся регионы - это те регионы, которые способны наращивать экспорт, если его рост не сопровождается более быстрым ростом импорта. То есть, чем больше значение предельной склонности импортировать, тем большая часть эффекта мультипликатора остается за пределами региона [3].

В модели Э. Тирлвалла роль экспорта в обеспечении регионального роста обеспечивается тем, что экспорт поддерживает сбалансированность торгового баланса и в отсутствии иных механизмов позволяет финансировать объем импорта, необходимый для удовлетворения внутреннего спроса [2]. Если экспорт недостаточен для финансирования требуемого объема импорта, то возникнет нарушение равновесия торгового баланса региона, что в долгосрочной перспективе будет ограничивать импорт, потребности местной промышленности и в итоге - развитие региона.

Предполагая, что темп роста экспорта региона зависит от темпа роста доходов остального мира ( ), умноженного на эластичность спроса на экспорт региона по доходам остального мира ( ), а темп роста импорта ( m ) региона зависит от темпа роста региональных доходов (у_г), умноженного на эластичность спроса на импорт по доходам региона (/?), получаем следующее уравнение для равновесного торгового баланса региона:

^У« = Р Уг.

То есть, согласно логике закона, темп роста региона зависит от темпа роста доходов остального мира и от отношения эластичности спроса на экспорт по доходам остального мира к эластичности спроса на импорт по доходам региона:

∝

Уг =-^ yw-

Для стимулирования регионального роста необходимо поощрять структуру экономики, в которой присутствуют отрасли, экспорт товаров которых отличается высокой эластичностью спроса по доходам остального мира, а импорт - низкой эластичностью спроса по доходам региона. В итоге данная теория говорит о том, что импорт необходим для внутреннего производства, которому требуются первичное сырье и не производимые в регионе промежуточные товары, а экспорт важен для роста как непосредственный источник финансирования импорта [3].

Описанные выше модели игнорируют проблему пространства. Вместе с тем очевидно, что обмен всегда включает какие-то пространственные характеристики. С точки зрения учета пространственной структуры экономики, наиболее продвинутой и популярной моделью является модель П. Кругмана [4]. Данная модель представляется в виде системы уравнений, определяющих доход потребителей, индекс цен на промышленные товары, номинальные и реальные зарплаты рабочих в каждом регионе. В частности, доход потребителей определяется по следующему уравнению:

Y_T = цЛ_ги/_г + (1 — рР(р _г, (1) где Y_r - доход региона г, Л_г - доля занятых в базовом секторе экономики в регионе г; р_г -доля занятых в сфере услуг в регионе г, w_r - средняя заработная плата в регионе г, р -параметр спроса и технологии, а также определяет долю занятых в базовом секторе.

Высокий уровень р соответствует большей доле промышленных товаров в бюджете потребителей, более высоким фиксированным издержкам фирм и большей доле занятых в базовом секторе экономики. Рост р увеличивает интервал транспортных издержек, на котором полная концентрация промышленности в одном регионе устойчива [3].

Методы/методика исследования. В данной работе предпринимается попытка построения эконометрической модели производства районов Бурятии на основе описанной выше теоретической модели Кругмана. Модель строится на основе данных статистических бюллетеней «Социально-экономический мониторинг районов Республики Бурятия», подготовленных Территориальным органом Федеральной службы государственной статистики по Республике Бурятия за 2009-2012 гг.

Согласно уравнению 1 в эконометрическую модель будут включены следующие переменные: Y_r - объем отгруженных товаров собственного производства, выполненных работ, услуг собственными силами по промышленной деятельности по чистым видам экономической деятельности по организациям, не относящимся к субъектам малого предпринимательства, средняя численность работников которых превышает 15 человек, включая средние предприятия, тыс. руб.; w_T - среднемесячная заработная плата по организациям, не относящимся к субъектам малого предпринимательства, средняя численность работников которых превышает 15 человек, включая средние предприятия, руб.

Упомянутый выше статистический бюллетень не содержит детальной информации о численности занятых в разрезе видов экономической деятельности, и это затрудняет получение долей Л_г и р_г. Для получения их оценок использовались данные об объеме отгруженных товаров собственного производства, детализированные по видам экономической деятельности. Так, Л_г оценивалась как суммарная доля объема отгруженных товаров следующих видов экономической деятельности: сельское хозяйство, охота и лесное хозяйство, рыболовство, рыбоводство, добыча полезных ископаемых, обрабатывающие производства, производство и распределение электроэнергии, газа и воды, строительство, а р_т - как суммарная доля объема отгруженных товаров всех остальных видов экономической деятельности.

Для эконометрического моделирования объема производства использовалась следующая спецификация модели:

InYr = p • ln(Zrwr) + (1 — z) • (pr + er. (2)

Так как исходные статистические данные представлены в форме панели за 2009– 2012 гг., параметры p и (1—z) оценивались с помощью обобщенного метода наименьших квадратов со случайным эффектом (Random Effect).

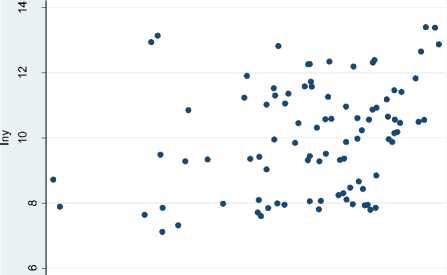
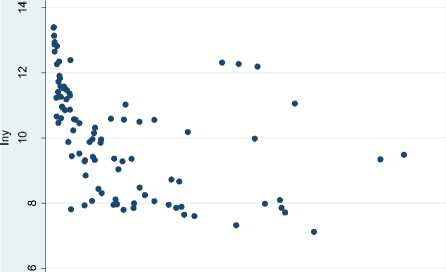
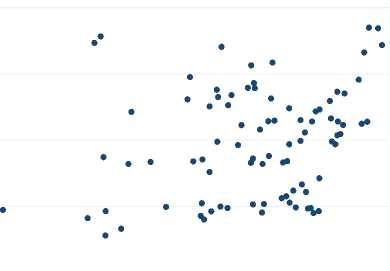
Результаты исследования. В ходе первичного визуального анализа данных удалось установить направление взаимосвязей между описанными выше переменными. На рисунке 1 представлены диаграммы рассеяния между логарифмом объемов отгруженных товаров собственного производства InY_r и логарифмом произведений средних зарплат на долю занятых в базовом секторе экономики Zn(A_rw_r) с учетом г. Улан-Удэ (рис. 1 а) и без (рис. 1 в); логарифмом объемов отгруженных товаров собственного производства InY_r и долей занятых в сфере услуг (р_г с учетом г. Улан-Удэ (рис. 1 б) и без (рис. 1 г). По диаграммам рассеяния видно, что с ростом взвешенной на средний уровень зарплат доли занятых в базовом секторе экономики объем производства растет, а с ростом доли занятых в сфере услуг – падает. При этом разброс точек на графиках а) и в) заметно выше по сравнению с б) и г), что в дальнейшем отразится на величине коэффициентов корреляции и интервальных оценках параметров модели.

В таблице 1 представлены результаты корреляционного анализа: коэффициенты парной и частной корреляции, рассчитанные с учетом г. Улан-Удэ и без. Вместе с тем зависимая переменная использовалась в двух видах – логарифм объемов отгруженных товаров собственного производства InY_r и он же на душу населения InY_r per capita. Величины рассчитанных коэффициентов и знаки перед ними подтверждают предположения, сделанные в ходе графического анализа данных: наличие прямой связи между InY_r и Zn(A_rw_r) и наличие обратной связи между InY_r и p_r во всех вариациях этих переменных. По данным таблицы 1 видно, что с исключением из анализа данных о г. Улан-Удэ абсолютные значения коэффициентов и их достигаемый уровень значимости для переменных InY_r и Zn(A_rw_r) снижаются, а для переменных InY_r и p_r - растут.

4                   6                   8                  10

ln_w_lambda

0                 .2                 .4                 .6                .8                 1

phi

а)

ln_w_lambda

б)

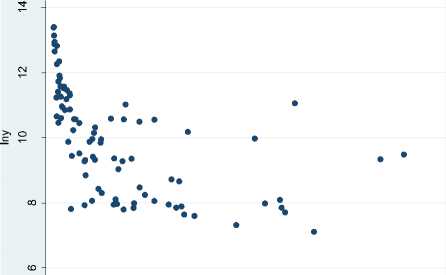
0                 .2                 .4                 .6                .8                 1

phi

в)

г)

Рисунок 1 - Диаграммы рассеянья для переменных lnY_r, ln(A_rw_r~) и ф_г.

Таблица 1 - Результаты корреляционного анализа

	Парная корреляция				Частная корреляция
	Включая Улан-Удэ		Без Улан-Удэ		Включая Улан-Удэ		Без Улан-Удэ
	lnYr	lnYr per capita	lnYr	lnYr per capita	lnYr	lnYr per capita	lnYr	lnYr per capita
In (Arwr)	0,339***	0.298***	0,34***	0,281***	0,239**	0,149	0,128	0,06
Фг	0,334***	0.445***	0,568***	0,548***	0,232**	0,373***	0,497***	0,492***

***, **, * – достигаемый уровень значимости коэффициента не хуже 0,01, 0,05, 0,1 соответственно

В таблице 2 представлены оценки параметров, их стандартные ошибки и коэффициенты детерминации четырех регрессионных моделей со случайным эффектом: с учетом г. Улан-Удэ и без, с абсолютным и душевым объемом производства в левой части уравнения 2. Все параметры значимы на уровне не хуже 0,1, а знаки при них корреспондируют с результатами корреляционного анализа. Параметры каждой модели можно интерпретировать как коэффициенты эластичности объема производства по переменным In (Arwr) и Фг . Более того, в модели Кругмана абсолютное значение параметра ф интерпретируются как доля товаров, произведенных базовым сектором экономики, в бюджете потребителей.

Таблица 2 - Оценки параметров регрессионных моделей со случайным эффектом

	lnYr включая Улан-Удэ		1п¥г без Улан-Удэ		lnYr per capita включая Улан-Удэ		lnYr per capita без Улан-Удэ
ц	0,0823	**	0,08201	*	0,0835	**	0,0815	*
	(0,0402)		(0,0428)		(0.0413)		(0.0435)
(1- ц )	-0,7584	**	-0,9569	***	-0,8159	**	-0,95898	***
	(0.3176)		(0.3538)		(0,3267)		(0,3598)
intercept	12,723	***	12,527	***	9,489	***	9,422	***
	(0,5075)		(0,4591)		(0,4753)		(0,4729)
R2	0,161		0,315		0,208		0,271

В скобках под параметрами указаны их стандартные ошибки.

***, **, * – достигаемый уровень значимости параметра не хуже 0,01; 0,05; 0,1 соответственно.

Выводы . Проведенный анализ данных позволил выявить взаимосвязи, описанные в теоретической модели Кругмана. Так, с ростом взвешенной на средний уровень зарплат доли занятых в базовом секторе экономики объем отгруженных товаров собственного производства растет, а с ростом доли занятых в секторе услуг – снижается. Причем, как видно на рисунке 1, первая взаимосвязь (рис. 1 а, в) менее очевидна, чем вторая (рис. 1 б, г). Корреляционный анализ показал, что изучаемые взаимосвязи чувствительны к исходному набору данных. Удаление из анализа данных о г. Улан-Удэ приводит к ослаблению первой взаимосвязи и усилению второй. Регрессионный анализ позволил оценить параметр μ, описанный в модели Кругмана. Его величина примерно одинакова для всех четырех регрессий из таблицы 2. Чего нельзя сказать о параметре (1-μ), абсолютное значение которого возрастает, если исключить из анализа г. Улан-Удэ – основного потребителя благ, производимых в секторе услуг. Наиболее высокое качество подгонки показала вторая модель из таблицы 2 с коэффициентом детерминации R ₌ 0,315, однако она не учитывает г. Улан-Удэ, и это вряд ли можно рассматривать как преимущество. Предпочтение следует отдать третьей модели, параметры которой значимо отличаются от нуля на уровне не хуже 0,05 при умеренном качестве подгонки R² = 0,208.