Моделирование электрохимической обработки металлов электродом-инструментом периодической структуры

Метод электрохимической обработки (ЭХО) металлов [3], в основе которого лежит процесс анодного растворения металла в проточном электролите, имеет широкое применение в различных отраслях машиностроения. В частности, метод ЭХО применяется для формирования на рабочих поверхностях теплообменных устройств рельефных поверхностей, предназначенных для интенсификации теплопередачи [1].

Для формирования регулярных рельефов на поверхности детали (аноде) можно использовать электрод-инструмент (катод) периодической структуры.

Пусть катод-инструмент образован бесконечной совокупностью прямоугольных выступов, совмещающихся друг с другом при параллельном переносе на некоторое конечное расстояние. Ниже, в рамках модели идеального процесса [3], находится численноаналитическое решение двумерной задачи, связанной с определением установившейся (стационарной) формы [3] поверхности детали.

Миназетдинов Н.М. Моделирование электрохимической обработки металлов...

Геометрия межэлектродного промежутка

Схема сечения межэлектродного промежутка представлена на рисунке 1.

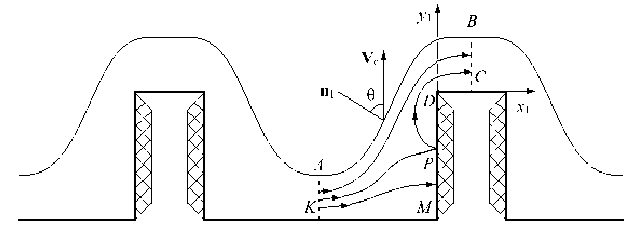
Рис. 1. Геометрия межэлектродного промежутка

Ограничимся рассмотрением области, расположенной между осями симметрии AK и BC . На ней: полигон KMDC – граница катода, отрезки KM и DC – токопроводящие (рабочие) участки катода, на участок DM нанесено диэлектрическое покрытие; линия AB – искомая установившаяся анодная граница. Система декартовых координат ( x ₁, y ₁) связана с катодом, и ее начало выбрано в точке D . Угол между вектором V _c скорости подачи катода и вектором n ₁ нормали к анодной границе равен θ. Длины отрезков CD , DM , MK обозначим как l ₁, l ₂ и l ₃ соответственно.

Модель процесса электрохимической обработки

Используя предпосылки и допущения модели идеального процесса, введем аналитическую функцию W j ( z 1 ) = v ( x 1 , y 1 ) + i u ( x 1 , y 1 ) комплексной переменной z 1 = x 1 + iy 1 . Действительная часть функции Re W ( z 1 ) = v ( x 1 , y 1 ) соответствует силовой функции электрического поля, а мнимая часть Im W ( z 1 ) = u ( x 1 , y 1 ) - потенциалу электрического поля в межэлектродном промежутке [6].

Потенциал u(x 1, y 1) принимает постоянные значения на границах электродов uAB=ua, uKM=uDC=uc.                            (1)

На осях симметрии AK , BC и участке DM границы катода, силовые линии электрического поля, ортогональны к ее эквипотенциальным линиям, и функция v ( x 1 , y 1 ) на указанных линиях принимает постоянные значения. На отрезке DM существует точка P ветвления эквипотенциальной линии, в которой напряженность электрического поля равна нулю [9].

Нормальная производная потенциала электрического поля на неизвестной установившейся анодной границе AB удовлетворяет условию [5]

д и    1 ( р V ^

----=---- 1 — a 1 +-- cos 9 ,                           (2) д n 1 К a 0 V £        )

где κ – удельная электропроводность среды; ε – электрохимический эквивалент металла; ρ – плотность материала анода; a ₀, a ₁ – постоянные, характеризующие свойства системы «металл – электролит».

26 в ыпуск 4/2020

Далее задача формулируется в безразмерных переменных:

v = ( u - u c )/( u a - u c ) , z = z 1/ H = x + iy , где ^ - безразмерный потенциал электрического поля; H = a _о к ( u a — u c )/ j 0 - характерная длина [8]; j 0 = p V /е - характерная плотность тока [4].

Тогда для функции W(z) = ф(x,y) + iv(x,у), где - ф(x,у) гармонически сопряженная функция по отношению к функции v(x,у), выполняются условия v|AB = 1, v|KM =v|DC =0;                            (3)

dW dv , a 1 ^ai

--- =——   = b + cos 9 , b = ——.

dz AB   ^d n AB                     ^j 0

На линиях AK , MPD и BC функция ф ( x , у ) принимает постоянные значения. Не нарушая общности, будем считать, что

ф| AK = ⁰, ф| MPD =%, Ф| BC = Фг

Согласно закону Ома плотность тока на границе электродов определяется по формуле

.     du к(ua— uc) dv j = к---=

Тогда

д n 1

- Г dv , H Г x , H T Фо = I , ds = —7-------7 I j (s) ds = —7

д n      KI u — u             кl u — u )

KM       acKM

C dv , H ^ф1 = I ^ds = 7        iAab ,

Ab dn     к( ua -uc )

то есть значения безразмерных постоянных величин ф ₀ и ф 1 характеризуют величины I KM и I_AB электрического тока, протекающего через границы KM и AB соответственно.

Задача сводится к определению безразмерных координат точек неизвестной установившейся анодной границы AB при выполнении условий (3)–(5).

Согласно гидродинамической аналогии [4, 7], двумерное потенциальное электрическое поле моделируется фиктивным плоскопараллельным потенциальным течением идеальной несжимаемой жидкости. При этом потенциалу электрического поля соответствует функция тока фиктивного течения, а функции тока – потенциал скорости. Гидродинамическим аналогом напряженности E электрического поля является скорость V фиктивного течения. Из условия (4) следует, что на искомой границе AB скорость фиктивного течения изменяется по закону

V = b + cos 9 , (6) где 9 - аргумент вектора скорости, совпадающий с углом между векторами V c и n 1 (см. рис. 1).

Численно-аналитическое решение задачи

Рассмотрим фиктивное потенциальное течение идеальной несжимаемой жидкости в односвязной области G z плоскости переменной z = x + iy , ограниченной анодной границей AB , полигональной границей KMDC катода и осями симметрии AK и BC . Поток

Миназетдинов Н.М. Моделирование электрохимической обработки металлов...

создается системой непрерывно распределенных источников вдоль линий AK , DP и стоков на линиях BC и MP . Схема расположения линий тока фиктивного течения представлена на рисунке 1. В точке P скорость фиктивного течения жидкости равна нулю.

1) (рис. 2), и буде

Для решения задачи введем вспомогательное комплексное переменное t = ^ + i 8, изменяющееся в области Gt = (111 < 1, 8 > 0 формно отображающую полукруг единичного радиуса на область течения. Соответству- м искать функцию z(t), кон-

ющие точки на рисунках 1 и 2 обозначены одинаковыми буквами.

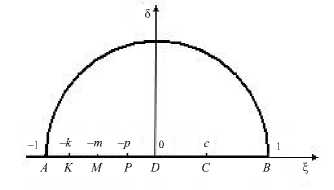
Рис. 2. Плоскость вспомогательной переменной t

Комплексный потенциал W ( t ) = ф ( t ) + i ^ ( t ) удовлетворяет условиям

1, t = exp ( i o ) , О е [ 0, п ] ,

0, t = ^,        ^ е [-k, -m] u [0, c].

0,

ф(^) = 1Фс,

Ф 1 ,

^е ^-1, — k], ^е [-m, с], ^е [ c, 1].

где О - полярный угол в плоскости параметрической переменной t . Область изменения комплексного потенциала представлена на рисунке 3, a .

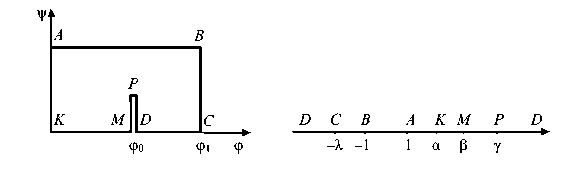
a                                 b

Рис. 3. Вспомогательные области:

а – область изменения комплексного потенциала W ; b – область изменения вспомогательной переменной u

Связь между переменной t и комплексным потенциалом W определяется методом конформных отображений [7]. Отобразим область Gt на верхнюю полуплоскость Gu

(рис. 3, b ) преобразованием [7]

u = —

Выпуск 4/2020

Используя интеграл Кристоффеля – Шварца [7], найдем производную функции, отображающей область G_u на область изменения комплексного потенциала:

dW

u —Y

---= N .               = du      (jU. u + ^)( u — a)( u — P)(

a =

u2 — 1)

Г 1

, N = const.

A

Y = - P +-

2 1 P

Используя формулы (7) и (8), получим dW     F(t)

---= M ,    , M = const; dt     t — — c

(t + p )(1 + tp)

F ( t ) =

.

Интегрируя выражение (9) на отрезке [ — k , — 1 ] , найдем величину M :

M = 1 , 1 . = J Fx )      dx,

I о       0 4 ( x ^{— k} )( ^{x — m} )

Fi( x )    --------( x — p )(1 — xp )---------

Jx (x + c )(1 +x c )(1 — x k )(1 — x m)

.

Интегрируя выражения (9) на отрезках [ — k , — m ] и [0, c ], найдем ^ф о = 1 1 / I 0, 1 1 = J 1, V =r dx ^;

m V(k— x )(X—m )

с

Ф 1 = Ф о ⁺ I 2/ I 0 , I² = J

F ( x)dx

0 dW

Из условия J dtpO^ = 0 следует,

— m

m

J

что

F ₁( x ) dx

.

— x

(k — x)(m — x)

= 0.

Введем в рассмотрение функцию Жуковского [2]

X ( t ) = ln V— = r + i 9 , r = ln V ⁰, dW           V

где V – модуль скорости; V ₀ – значение скорости в точке B ( t = 1). Из формулы (6) следует, что V ₀ = b + 1.

Представим функцию % ( t ) в виде суммы [2]

Х( t )=%0 ( t ) +®( t ) ,

где Х ₀ ( t ) = r ₀ + i 9 0 - функция Жуковского для вспомогательного течения жидкости по заданной схеме при условии, что на границе AB модуль скорости постоянны й и равен V ₀; w ( t ) - функция, аналитическая в области G_t и непрерывная в ее замыкании G_t [7].

Миназетдинов Н.М. Моделирование электрохимической обработки металлов...

Согласно схеме течения, функции % ( t ) и

Х 0 ( t ) удовлетворяют следующим граничным

условиям:

Im % ( ^ ) = Im Х о ( ^ ) = '

0,     ^^е[^{- 1,} - p ) и ( 0,^{1 ]} ,

^—п , ^^e ( ^— p , ⁰ ) .

V0exp(—r(t)) = b + cos6(t), r0(t) = 0, t = exp(io), oe^Q,n]; r(1) = 0.(17)

Функции x ( t ) и X 0 ( t ) имеют логарифмические особенности в точках P ( t = — p ) и D ( t = 0 ) . По известным граничным условиям и известным особенностям функцию Х ₀ ( t ) можно построить методом особых точек Чаплыгина [2]:

, .        t(1 + tp),

%0 (t ) = ln-4---Ц t + p

Согласно формулам (16), (17) из соотношения (15) следует, что функция w ( t ) долж-

на удовлетворять условиям

Im w ( £ ) = 0, ^e[— 1,1 ] ; Re w ( 1 ) = 0;                  (19)

b + cos ( 6 0 ( o ) + Ц ( о ) ) — V ₀ exp ( —v ( o ) ) = 0;                  (20)

^ ( o ) = Im ГО ( exp ( i o ) ) , v ( o ) = Re w ( exp ( i o ) ) .

Из условий (19) следует, что согласно принципу симметрии Шварца функцию w ( t ) можно аналитически продолжить на весь круг | t | < 1 и искать ее в виде [7]

^

»(t )=^ о/,(21)

к = 0

где c_k – вещественные коэффициенты, удовлетворяющие равенству

^^

ю(1)=^ck = 0 или с0 = Xck.

к=0

Всюду далее суммирование ведется от к = 1 до к = ^ .

Геометрические характеристики течения определяются из параметрической зави-

симости

dz = exp ( x ( t ) ) dW = M F 2 (t ) dt       V ₀      dt    V ₀ V t — c ’

F 2 ( t ) =

( ^{1 +} tp ) ² y t exp ( c 0 ⁺ ^ ^c k ^{t k} )

( 1 — tc ) ( t + к ) ( 1 + tk ) ( t + m ) ( 1 + tm )

Интегрируя выражение (23) на отрезках [ 0, c ] , [ — m , 0 ] , [ — к , — m ] , найдем безразмерные длины отрезков CD , DM , MK :

L = ^ 1 H

¹ Г F 2 ⁽ x ) J..

dx ;

I 0 V 0 о V c^x

—

L = -2 H

-J- J - F 3i x L dx ; I 0 ^V 0 0 V m ^{— x}

—

L ₃ =-3 H

^J "-- x ¹ dx; F , ( x ) =

I n V V x — m 00 m

—

(^{1 —} xp ) 2 V x ^exp ( c 0 + ^ ^(— 1 ) ^к С_кХ ^к )

x + c ) ( 1 + xc ) ( к — x ) ( 1 — хк )( 1 — xm )

30 в ыпуск 4/2020

Для численного решения задачи задаются значения коэффициента a , характерной плотности тока j 0 = p V . /е и геометрических параметров L 1 , L 2 и L 3 . Коэффициенты разложения (21) и параметры k , m , p , c определяются таким образом, чтобы на искомой анодной границе удовлетворялось условие (20) и выполнялись соотношения (13) и (24). Для этого в разложении (21) сохраняется конечное чис ло n слагаемых, а уравнение (20) выполняется в дискретных точках О _к = п к^ , где к = 1, n . Система уравнений относительно параметров с_к , к = 1, n решается совместно с уравнениями (13), (24) методом Ньютона.

После определения коэффициентов с_к , к = 1, n и параметров к , m , p , с безразмерные координаты точек анодной граница AB определяются с помощью соотношения (23) при условии,что t = exp ( i o ) , Ое [ 0, п ] .

Результаты расчетов

Введем обозначения: L ₄, L ₅ – безразмерные величины межэлектродного зазора в сечениях AK и BC соответственно; y_A - ордината точки A ; L 6 = | y_A | + L 5 - высота выступа, полученной стационарной анодной границы AB .

В качестве примера рассмотрим случай, когда а1 = -12,818, j0 = 100 А/см2, L1 = 1, L3 = 2.

В таблице 1 представлены результаты расчетов величин: L ₄, L ₅, y_A , L ₆, φ ₀, φ ₁ для трех различных значений L ₂: 1,8; 2,0; 2,2.

Таблица 1

Результаты расчета параметров

L 2	L 4	L 5	yA	L 6	φ 0	φ 1
1,8	1,0669	0,809	–0,7331	1,5421	1,4249	3,4557
2,0	1,077	0,8075	–0,923	1,7305	1,4152	3,4758
2,2	1,0808	0,807	–1,1192	1,9262	1,4146	3,4958

На рисунке 4 представлены графики анодных границ для указанных случаев.

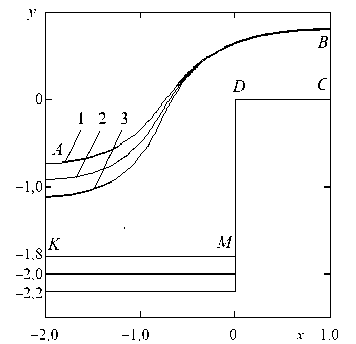
Рис. 4. Результаты расчета анодных границ: 1 – L ₂ = 1,8; 2 – L ₂ = 2,0; 3 – L ₂ = 2,2

Миназетдинов Н.М. Моделирование электрохимической обработки металлов...    31

Рассмотрим случай, когда a1 = -12,818, j0 = 100 А/см2, L1 = 1, L2 = 2.

В таблице 2 представлены результаты расчетов величин L ₄, L ₅, y_A , L ₆, φ₀, φ₁ для трех различных значений L ₃: 1,5; 2,0; 2,5.

Таблица 2

Результаты расчета параметров

L 3	L 4	L 5	yA	L 6	φ 0	φ 1
1,5	1,383	0,8084	–0,671	1,4794	0,847	2,891
2,0	1,077	0,8075	–0,923	1,7305	1,4152	3,4738
2,5	0,9633	0,8078	–1,0367	1,8445	1,9813	4,0426

На рисунке 5 представлены соответствующие графики анодных границ.

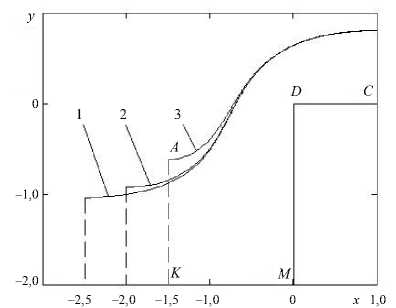
Рис. 5. Результаты расчета анодных границ: 1 – L ₃ = 2,5; 2 – L ₃ = 2,0; 3 – L ₃ = 2,5

Заключение

На основе математической модели процесса электрохимического формообразования, описанного в работе [5], решена задача расчета координат точек установившейся анодной границы при обработке катодом-инструментом заданной формы, имеющей периодическую структуру. Результаты решения позволяют сделать выводы о влиянии геометрических размеров катода на размеры выступов, получаемых в результате электрохимической обработки рельефной поверхности.