Моделирование электромагнитного поля с помощью метода конечных разностей

Интенсивное использование электрической энергии привело к тому, что в последней трети XX века сформировался новый значимый фактор загрязнения окружающей среды - электромагнитный. В связи с увеличением числа источников электромагнитного поля (ЭМП) опасность их воздействия на людей возрастает. Обеспечение электромагнитной безопасности является актуальной гигиенической проблемой в условиях повсеместной автоматизации технологических процессов. Поэтому актуальной проблемой является оценка уровней электромагнитных излучений (ЭМИ) в местах пребывания и продолжительного нахождения людей.

Процесс оценки степени воздействия электромагнитного поля на человека можно разделить на три этапа:

• -    измерение параметров ЭМП в обследуемом помещении;

• -    компьютерное моделирование ЭМП с целью получения полной картины электромагнитной обстановки;

• -    анализ полученной картины, оценка опасности для человека.

Измерение параметров ЭМП может быть произведено с помощью различной аппаратуры как отечественного, так и зарубежного производства [1]. Большинство современных приборов позволяет единовременно фиксировать эти параметры только на одной частоте. Тем не менее для составления полной картины электромагнитной обстановки в области пространства необходимо иметь данные по широкому спектру частот (в идеале - по всем частотам ЭМИ в помещении). С этой целью в Алтайском государственном техническом университете ведутся работы по созданию многофункциональных приборов, позволяющих, в частности, представлять параметры ЭМП в виде ряда Фурье.

Для выполнения компьютерного моделирования ЭМП по результатам измерений с помощью приборов как первого, так и второго типов может быть использован следующий подход.

Переменные электромагнитные процессы соответствуют уравнениям Максвелла [2-4]. Решение системы дифференциальных уравнений Максвелла в пространстве является достаточно сложной задачей, но с развитием ЭВМ стали доступны численные методы, которые позволяют эффективно её решить.

Одним из таких методов, применяющимся на сегодняшний день, является метод конечных разностей во временной области (finite-differencetime-domainmethod, далее метод FDTD) [5]. В основе метода лежит алгоритм Йи [6].

Суть конечно-разностных методов состоит в замене частных производных в каждой точке пространства конечными разностями, зависящими от значений параметра в соседних точках пространства. Метод ко-иечных разностей во временной области добавляет также временное измерение.

Данный метод позволяет провести симуляцию (модельный эксперимент) и проследить эволюцию электромагнитного процесса во времени.

Метод FDTD основывается на уравнениях Максвелла для области, не имеющей свободных электри-ческих и магнитных зарядов [7].

Закон Фарадея

Энергообеспечение и энерготехнологии

VxE+^=-M.

Закон Ампера

Vx " + !=/•(2)

Закон Гаусса для электрического поля

• V    • D = 0.(3)

Закон Гаусса для магнитного поля

• V    • В = 0.(4)

В выражениях (1)-(4) приняты следующие обозначения:

Е - напряжённость электрического поля;

D - плотность электрического потока;

Н - напряжённость магнитного поля;

В - плотность магнитного потока (вектор магнитной индукции);

/ - плотность электрического тока;

М - плотность эквивалентного магнитного тока.

Буквой V обозначен оператор Гамильтона [8].

Самый простой вариант алгоритма Йи позволяет моделировать развитие электромагнитного процесса внутри вещества, обладающего линейными изотропными недисперсными электромагнитными параметрами, откуда следуют два важных равенства:

D = еЁ = £_г£оЕ>                                       (5)

В = pH = р_гр₀Н,                                  (6)

где е - диэлектрическая проницаемость материала;

е_г - относительная диэлектрическая проницаемость материала;

е0 - диэлектрическая проницаемость вакуума;

р - магнитная проницаемость материала;

р_г - относительная магнитная проницаемость материала;

д0 - магнитная проницаемость вакуума.

Метод FDTD позволяет задавать источники электрического и магнитного поля внутри рассматриваемой области пространства, а также симулировать электрические и магнитные потери в веществах. В связи с этим параметры/и М из уравнений (1)—(4) могут принять следующий вид:

/ ^— /source “Г ^б,                                             (7)

М = M_source + а^тН,                                 (8)

^гД^е /source ~ плотность тока источника;

о - электрическая проводимость материала;

^source ~ плотность эквивалентного магнитного тока источника;

а^т - эквивалентные магнитные потери.

Подставляя выражения (5)-(8) в уравнения (1)-(4), получим:

^ = _1_VXB^1 (M_source + _ат^.                     (9)

d^ = --vxH-^(/source + aE).                        <10)

Для отдельных компонентов векторов получим шесть связанных уравнений Максвелла р]:

dHx _		1 /	'dEy	dEy	-°mHx	— ^sourceX)«	(ID
dt		д'	< dz	dy
дНу			(dEz	dEx		— ^sourceY^ <	(12)
dt		д’	k dx	dy
dHz		Ч	'dEx	dEy		“ ^sourceZ^'	(13)
dt		д'	< dy	dx	О Hz
dEx			(dHy	dHy		~ JsourceX^ I	(14)
dt		£	I dz	dy	° bx
dEy		1	(dHz	dHx			(15)
dt		£	I dx	dy		J sourceY J >
dEz		1	(dHx	dHy		~ J sourceZ^-	(16)
dt		8	\ dy	dx

Ключевой особенностью алгоритма Йи является расположение векторов напряжённости электрического и магнитного поля внутри векселя (вексель - элементарный фрагмент пространства в конечноразностных методах). Это может быть проиллюстрировано рисунком.

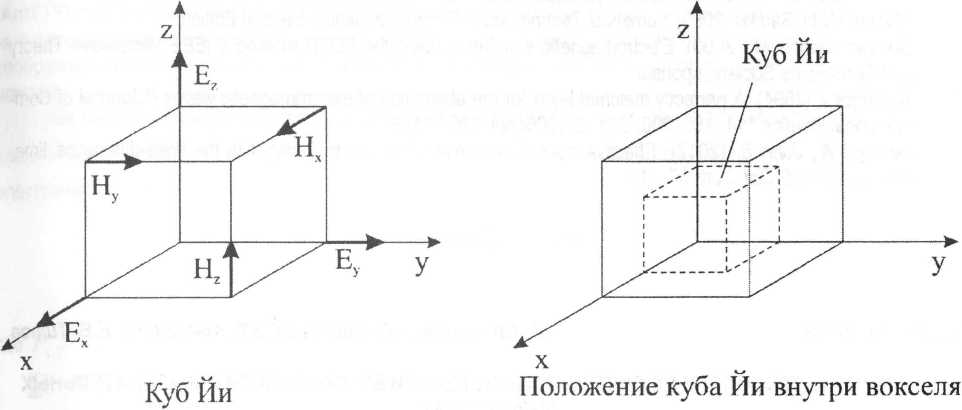
Расположение векторов Ей Нна кубе Йи

Векторы Е и Н разнесены не только в пространстве, но и во времени на половину модельного временного шага [7,9,10].

Метод FDTD предполагает задание частично рассеивающих или отражающих условий для граничных областей модельной области. Для моделирования помещения целесообразно разместить на границах модельной области так называемые идеально согласованные слои (perfectly-matchedlayers) [10,11].

Существуют готовые открытые и коммерческие реализации метода FDTD для моделирования электромагнитного поля, а также для других областей науки и техники (например, [12]). Эти реализации позволяют проводить анализ электромагнитных полей различных конфигураций в различных условиях, получать параметры поля для конкретных точек помещения или интегральные показатели. Также возможно графическое представление картины электромагнитной обстановки в любой момент времени (или интегрально для всего рассматриваемого промежутка времени).

После проведения отдельного модельного эксперимента с применением метода FDTD для каждого источника ЭМИ в помещении может быть выполнен анализ результирующего параметра поля от всех источников ЭМИ.