Моделирование электропривода на основе трехфазного асинхронного двигателя с частотным управлением

Современные системы векторного управления прошли долгий путь развития и в настоящее время являются наиболее распространенными среди систем электропривода переменного тока. Они позволяют просто и эффективно управлять такими сложными объектами как асинхронный двигатель с короткозамкнутым ротором (АКЗ), что в свою очередь, позволяет существенно расширить область его применения, почти полностью вытесняя из автоматизированных управляемых приводов двигатели постоянного тока. Это связано в первую очередь с развитием силовой электроники, позволяющей создавать надежные и относительно дешевые преобразователи, а также с развитием быстродействующей микроэлектроники, способной реализовать алгоритмы управления практически любой сложности. Поэтому высококачественный асинхронный векторный электропривод (АВП) в настоящее время является по существу техническим стандартом.

Асинхронный двигатель с короткозамкнутым ротором (АКЗ) уже около 100 лет используется и будет использоваться как практически единственная реализация массового нерегулируемого электропривода, составляющего до настоящего времени более 90% всех промышленных электроприводов. В последнее десятилетие благодаря успехам электроники (преобразователи частоты) короткозамкнутый асинхронный двигатель стал основой частотно-регулируемого электропривода, успешно вытесняющего доминировавший ранее электропривод постоянного тока во многих сферах.

Применение такого электропривода особенно важно для решения задачи автоматизации ленточных конвейеров. В силу специфических условий работы электрооборудования на горных предприятиях электропривод постоянного тока практически не находит применения в качестве привода ленточных конвейеров. Абсолютное большинство действующих в стране конвейерных установок снабжено электроприводом на основе асинхронного двигателя с короткозамкнутым (АКЗ) и с фазным ротором (АДФ). Существуют схемы электроприводов на основе АКЗ и

АДФ, которые применяются или могут найти в будущем широкое применение в горной промышленности.

Обобщенный асинхронный двигатель с трехфазной обмоткой на статоре и трехфазной обмоткой на роторе изображен на рис. 1. Модель асинхронной электрической машины составим согласно известному методу, приведенному в работах [1, 2, 4].

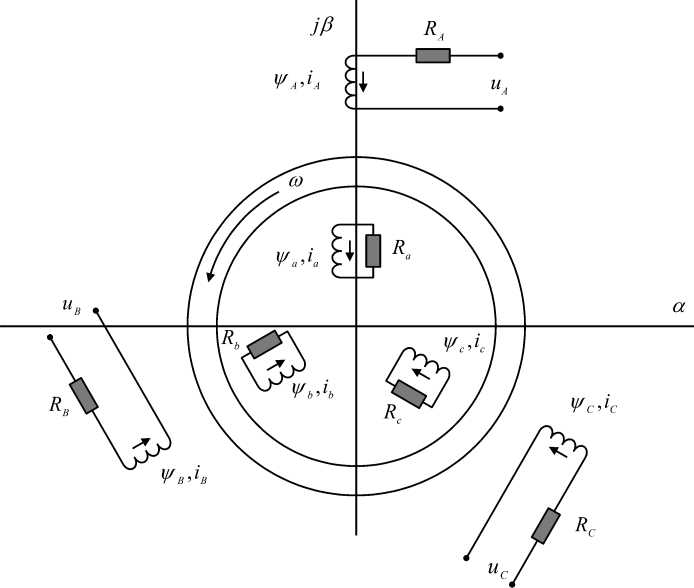
Рис. 1. Обобщенная асинхронная машина.

Обмотки статора и ротора в общем случае подключены к симметричным трехфазным источникам напряжения.

Уравнения равновесия ЭДС на обмотках статора и ротора базируется на втором законе Кирхгофа.

Для статора:	Для ротора:
dA uA   RAiA         , dt	ua   Raia +d a , dt
u    Ri - + d^ B uB   RBiB         , dt	d^ь ub   Rbib +       , dt	>         (1)
d^с u    RCiC +       . C    C C     dt	d^с u  Ri+ c      cc          . dt

В уравнениях (1) фигурируют мгновенные напряжения, токи и потокосцепления статора и ротора, а также активные сопротивления обмоток. Обычно обмотки выполняются симметричными, и поэтому R А =R В =R С =Rs - активное сопротивление статорной обмотки, R а =R b =R с =R R - активное сопротивление роторной обмотки.

Вторым используемым законом является закон Ампера, который связывает потокосцепления обмоток с токами, протекающими по обмоткам:

Для статора:

VA ^{= L}aA'A ^L A^ i B ^LAC^C ^LAa^a ^"LAbb "^LAc k ,

^B -L B^-A "^LBB-B "^LBb-C "^LBba ^L^bb ^{+ L} Bc i c , ^>  A ~ ^LCA ^- A ^L^B^B ^LCC^C ^LCak ^{+ L} Cb ^- b +^Lcbc • , Для ротора:

(2а)

V a ⁼ L aA i A ^L aBB + ^LaC i C ^L aa^a + L ab i b ^{+ L}abc ,

W b ⁼ L bA i A ^{+ L}bB i B ^{+ L}bC i C ⁺ L ba i a ⁺ L bb i b ⁺ L bc i c , ^>

(2б)

показывают, что

Vc ⁼ L cA i A ^+LcB^B ^{+ L} cck + ^L cba ^{+ L} cb i b ^{+ L}cc i c • ,

Уравнения для определения потокосцеплений потокосцепление каждой обмотки зависит от токов во всех обмотках; эти зависимости проявляются через взаимоиндукцию. В уравнениях (2) LAA, Lbb, LCC, Laa, Lbb, Lcc, являются собственными индуктивностями соответствующих обмоток, все остальные - взаимоиндуктивностями между соответствующими обмотками.

Третьим законом, лежащим в основе анализа, является второй закон Ньютона - закон равновесия моментов на валу машины:

j^ m= M-M С ,                                    (3)

dt где J (кг-м2) — момент инерции на валу машины, учитывающий инерционность как самой машины, так и приведенной к валу rad инерционности рабочего механизма и редуктора,  ют(—) - угловая

с скорость вала машины, M с(Н м) - момент нагрузки рабочего механизма, приведенный к валу, в общем случае он может быть функцией скорости и угла поворота.

Наконец, четвертым и последним законом, лежащим в основа анализа машины, является закон, сформулированный Ленцем, как правило левой руки. Этот закон связывает векторные величины момента, потокосцепления и тока:

M = k (у Ai ) .                                                  (4)

Следует сразу подчеркнуть, что, несмотря на полное и строгое математическое описание, использование уравнений (1)  -  (4) для исследования машины встречает серьезные трудности. Из них основные:

• -    в уравнениях (3 и 4) фигурируют векторные величины, а в уравнениях (1 и 2) скалярные;

• -    количество взаимосвязанных уравнений равно 16, а количество коэффициентов - 44;

• -    коэффициенты взаимоиндукции между обмотками статора и ротора в уравнениях (2) являются функцией угла поворота ротора относительно статора, то есть уравнения (2) являются уравнениями с переменными коэффициентами;

• -    уравнение (4) является нелинейным, так как в нем перемножаются переменные.

На пути упрощения математического описания асинхронной ма-шины, да и вообще всех машин переменного тока, удивительно удачным и изящным оказался метод пространственного вектора , который позволил существенно упростить и сократить вышеприведенную систему уравнений; метод позволяет связать уравнения (1-4) в единую систему с векторными переменными состояния. Суть метода состоит в том, что мгновенные значения симметричных трехфазных переменных состояния (напряжения, токи, потокосцепления) можно математически преобразовать так, чтобы они были представлены одним пространственным вектором.

Это математическое преобразование статора):

i = (i A iA^aiB^a i C ),

имеет вид (например, для тока

24 j 2 j где a e ³ , a e ³

—

векторы,

смещение    обмоток,     i I cos t ,

учитывающие пространственное iB = Im COS(®t - —), ic = Im cos^t + —) -

симметричная трехфазная система токов статора.

Подставив в уравнения (5) значение мгновенных токов, найдем математическое описание пространственного вектора статорного тока:

i S I (cos t e ³ cos( t      ) e ³ cos( t       )) I e ^{j t} .

На рис. 2.1 представлена геометрическая интерпретация пространственного вектора тока - это вектор на комплексной плоскости с модулем (длиной) I m , вращающийся с угловой скоростью (о в положительном направлении. Проекции вектора i s на фазные оси А, В, С определяют мгновенные токи в фазах. Аналогично пространственными векторами можно представить все напряжения, токи и потокосцепления, входящие в уравнения (1.1), (1.2).

Теперь можно переходить к упрощению уравнений.

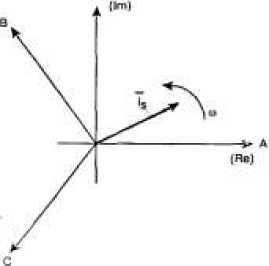
Рис. 2. Пространственный вектор тока.

Шаг первый. Для преобразования уравнений (1) в мгновенных значениях к уравнениям в пространственных векторах умножим их на

2-

2   -2

выражения: первые уравнения на -, вторые - на j a , третьи - на - а , - и

сложим раздельно для статора и ротора. Тогда получим: d u S — Rg iS "I,

S      dt d ur=Rrir-\--,    ^

dt

S =LSⁱs+Lm Ф)iR ,

V R =Lm Ф) IS+LRIR ,, где LS, Lr - собственные индуктивности статора и ротора, Lm(9) - взаимная индуктивность между статором и ротором. Таки образом, вместо двенадцати уравнений (1)-(2) получено лишь четыре уравнения (7).

Шаг второй. Переменные коэффициенты взаимной индукции уравнениях для потокосцеплений (7) являются результатом того, что уравнения равновесия ЭДС для статора записаны в неподвижно системе координат, связанной со статором, а уравнения равновесия ЭДС для ротора записаны во вращающейся системе координат, связанной с ротором.

Метод пространственного вектора позволяет записать эти уравнения в единой системе координат, вращающейся произвольной скоростью к. В этом случае уравнения (7) преобразуются к виду:

d

U S =^RS i S+—-S + y ty^ S , dt

d

UR =RrIr +---R + J (ta k - O)RR A dt

У S ^SiS+LjR ,

^ R=LmiS+LRiR ,               , где о = рчйm, р - число пар полюсов в машине.

В уравнениях (8) все коэффициенты являются величинами постоянными, имеют четкий физический смысл и могут быть определены по паспортным данным двигателя, либо экспериментально.

Шаг третий. Этот шаг связан с определением момента. Момент в уравнении (4) является векторным произведением любой пары векторов. Из уравнения (8) следует, что таких пар может быть шесть ( i s , i R ); (у _s , y/_R ); (i s , ^ _s ); ( i s , i^_R ); (I r , yS ); ( i R , ^ _R ) . Часто в рассмотрение вводится потокосцепление взаимной индукции L_mi=L_m ( 1s+1 r ) . В этом случае появляется ещё четыре возможности представления электромагнитного момента машины через следующие пары:

( is , ^); ( I r , y_m ); (^ s , y_m ); (у/ r , ^ m ) . После выбора той или иной пары уравнение момента приобретает определенность, а количество уравнений в системе (8) сокращается до двух. Кроме того, в уравнениях (3) и (4) векторные величины момента и скорости могут быть заменены их модульными значениями. Это является следствием того, что пространственные векторы токов и потокосцеплений расположены и плоскости, перпендикулярной оси вращения, а векторы момента и угловой скорости совпадают с осью. В качестве примера запись уравнений момента

через некоторые пары переменных состояния машины имеет вид:

,,    3   ,    _    -    ♦

M = -pL_m -Mod ( is X iR ),

_  3              x

M = pp-Odod(y/_s x is ),

M = pP^R MOod(y/_R x is ).

В конечном виде уравнения обобщённой асинхронной машины

имеют вид:

d uS   RSiS        S j k S , dt

d uR   RRiR       R j( k p m) R, dt

_S   L_S i S    L_m i R ,

_R   L_m i S    L_R i R ,

M    p k Mod (     i k ),

J ^{d m} M M .

dt            ^С

Уравнения асинхронной машины с короткозамкнутым ротором или машины с фазной обмоткой, если к ней не подключено питающее напряжение, можно получить из уравнений (10), если в этих уравнениях

положить U r = 0 .

d us =Rsis +—— + j®ky/s, dt

d

• ⁰ = R R i R +—-R + j ⁽® _k- pO m )v R , dt

• У⁷ s ^{= L}s^is +Lm^iR ,

R ^{= L}m^is +^LR^iR ,

M = pp-k-Mod(\Pi xi_k ),

• j^dl^m₌ M-M_c .

dt            ^С

Для динамических систем необходимо учитывать переходные электромагнитные процессы в машине. В этом случае в качестве пары переменных, описывающих машину, оставим пространственные векторы тока статора и потокосцепления ротора ( is,v_R ), тогда уравнения (11) с учётом уравнений для потокосцеплений (8) после соответствующих преобразований примут вид:

• -        • . т ■ dis , • „ т *.     ^kR - ,

• us =rls +Ls— + jOkLSlS -—VR+jkRP®mVR , dtT

0 = kRRRRlS +—Vr ^—PR^J (tok -P®m )V R , Tdt

3   ,   _   -*

M = pp-k_R MOd((v_R x i s ),

Jd^m = M-Mc, dt

_   L2 _         _    L2   . L L, где r = Rs+ -pRRR, Ls=Ls~-pr, kR=-p, TR="pR — коэффициенты.

LR              LR       LR       RR

Для синтеза и анализа электропривода, построенного на базе асинхронного короткозамкнутого двигателя решающим является выбор системы координат. При построении реальных систем электроприводов переменного тока практически всегда в систему управления включают преобразователи координат. Это обусловлено тем, что реализация регуляторов возможна лишь во вращающейся системе координат, а реальные токи в обмотках статора – это токи в неподвижной системе координат. Используя при математическом описании электропривода вращающуюся систему координат, удается существенно упростить описание и моделирование, так как не возникает необходимости в преобразователях из вращающейся системы и обратно, а также в преобразователях фаз 2/3 и 3/2.

Во вращающейся с относительной угловой скоростью в системе координат с вещественной осью “x” и мнимой осью “y” уравнения (12) в операторной форме запишутся в виде:

k usx = r(1 + Tss)lsx - KL:Lsysy -^RVRx- kRPtomVRy,

TR uSy = r(1 + TSs) lSy + KrI^sXsx -bRVRy^" kRPtomVRx

T _R

• ⁰    = k^kRRisXsx + 1- R^. "^V. - ⁽®k - P®m ) ^Ry ,

T _R

• ⁰    = ^kkR^Rsy_Sy + 1- Ry_Rys s^Ry + ⁽®k - po_m ) ^Rx , T _R

• m    = ^L5 P^k R ⁽ Wsy -VRy i Sx ) ,

Js    M M .

Структурная схема АКЗ и ее модель зависит от выбора базового вектора, который определяет скорость вращения координат. За базовый вектор принимается тот, который при анализе совмещается с одной из осей системы координат.

Так если за базовый вектор принять вектор u , то система координат будет вращаться со скоростью й) равной угловой частоте напряжения питания. Кроме того, если совместить вектор u с осью x вращающейся системы координат, то в уравнениях (13) следует принять ^usx ^U 1 ^{, u}sy ^0.

k

U ₁ r (1   T _S s ) i _{Sx    1} L _S i _Sy         Rx  ^kR^p (О m У _Ry ,

T _R

0 r (1 + ^TS ^{s ) i}Sy    1 ^LS ⁱSx     ^R -^Ry +k _R p (О mW Rx

T _R

0     k_RR_Ri_Sx +¹ -VRx +^s^ Rx  ( (О 1 ^p(Оm ) VRy ,                       (14)

T _R

0     k _R R _R i _Sy +¹-^ Ry +^sVRy +⁽ (У1 ^p(Оm )^ Rx ,

TR m  1.5 pkR (V RxiSy -V RyiSx ) ,

Js о m^{M M}H .

Моделирование проведено в пакете прикладных программ Simulink.

Структурная схема, построенная по уравнениям (14) представлена на рис. 3.

Для моделирования выберем АКЗ 20HP (15kW) из библиотеки Sim Power System со следующими паспортными данными и параметрами: U 400 B , f  50 Гц, R S 0.2147 Ом., R 0.2205 Ом., LL 0.06518 Гн,

AB              S           R           SR

L 0.06419 Гн, J= 0.102 кгм² , p=2.

Коэффициенты, необходимые для моделирования уравнений помещены в табл. 1.

Таблица 1.

Коэффициенты	r	T S 1	т R	kR	L S
Един.измерения	Ом	с	с		Гн
Значение	0.4285	0.0046	0.2956	0.9848	0.00196

Результаты моделирования представлены на рис. 4. В этой модели напряжение питания и частота, являясь переменными режима, могут изменяться независимо друг от друга.

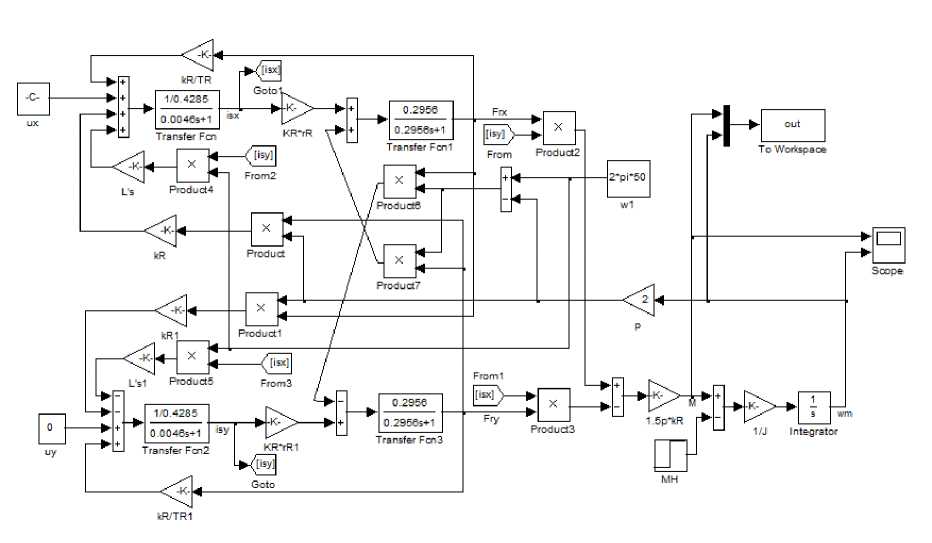
Рис. 3. Модель АКЗ во вращающейся системе координат с базовым вектором напряжения.

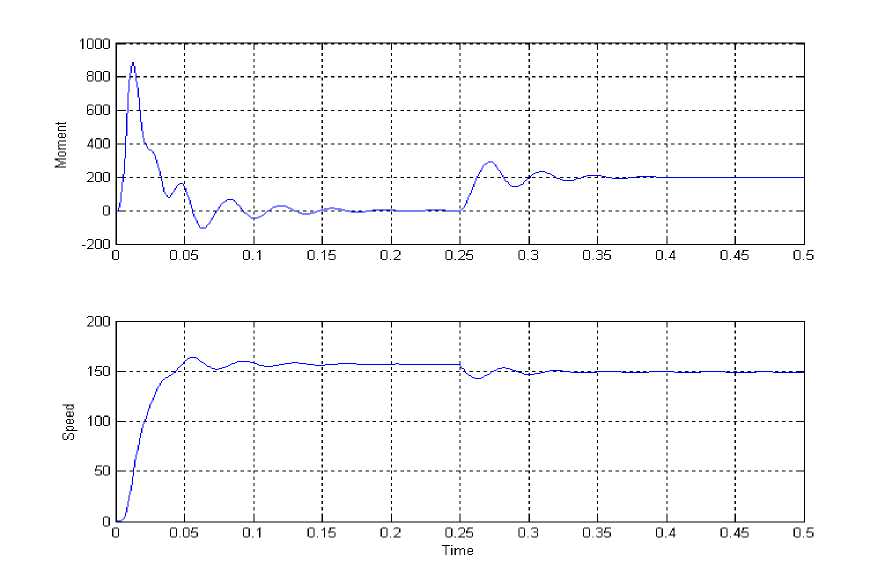
Рис. 4. Переходные процессы в АКЗ при пуске и набросе нагрузки.

Результаты моделирования, приведенные на рис. 4, показали, что при прямом пуске привода с постоянной нагрузкой наблюдаются значительные колебания момента и скорости. Кроме того, наблюдается значительное падение скорости под нагрузкой, то есть ошибка отработки задания.

Математическое описание АКЗ во вращающейся системе координат, совмещенной с вектором напряжения является основой для синтеза асинхронных систем с частотными способами управления.

асинхронный электродвигатель c короткозамкнутым ротором, математическая модель, переходные процессы, метод пространственного вектора, вращающаяся система координат three-phase asynchronous machine with a squirrel cage, mathematical model, transitional processes, method of space vector, rotating coordinate system