Моделирование эволюции дислокационной подсистемы при деформации гетерофазных сплавов с некогерентной упрочняющей фазой

The model of a dislocation subsystem evolution in heterophase alloys, containing noncoherent particles, is considered. The model includes three differential equations of a balance for: l)matrix dislocations., 2)vacancies prismatic loops, and 3)interstitials prismatic loops. The qualitative research of the dynamic system and the parametrical analysis is carried out. The phase portraits are calculated.

В качестве базового структурного элемента при создании математических моделей пластической деформации удобно использовать зону элементарного кристаллографического сдвига, которая является связующим звеном между микро- и макропроявлениями пластичности [1-4]. В случае гетерофазных материалов дефектная структура зоны сдвига значительно сложнее, чем в чистых металлах и однофазных сплавах [5-9]. Помимо процессов, связанных с генерацией сдвигообразующих дислокаций, в этом случае развиваются элементарные процессы, обусловленные взаимодействием дислокаций с частицами недеформируемой упрочняющей фазы. Результатом такого взаимодействия является генерация новых типов дефектов - призматических петель, колец Орована, петель вторичного скольжения и др. [5-9].

В работе [9] показано, что для гетерофазных материалов с недеформируемыми частицами существует некоторая критическая плотность дислокаций рс, при превышении которой изменяется характер дислокационной структуры зоны сдвига. В условиях докритической плотности дислокаций смещение дислокаций в третьем измерении - в направлении нормали к плоскости скольжения - невелико, и расширение дислокационной петли, испущенной источником, можно рассматривать как двумерный процесс. При этом накопление сдвигообразующих дислокаций происходит на барьерах дислокационной природы, ограничивающих зону сдвига. Внутризонные протяженные барьеры отсутствуют. Модель дефектной подсистемы содержит в этом случае три уравнения баланса: 1) сдвигообразующих дислокаций, 2) вакансионных призматических петель, 3) межузельных призматических петель[9].

Генерация и размножение сдвигообразующих дислокаций с деформацией в гетерофазном материале могут быть описаны соотношением [1,2]:

I da Jg bD(pm,T2)

где Ct - деформация сдвига, p_m - плотность сдвигообразующих дислокаций, F - безразмерный параметр, определяемый геометрией зоны сдвига [1], D(p_m,T₂) - средний диаметр зон сдвига, ^ ~ сопротивление движению дислокаций во вторичных системах, b - модуль вектора Бюргерса.

Интенсивность генерации геометрически необходимых дислокаций с деформацией [9]

^Рр ^ da

Л2Ь

где < х > - средняя величина параметра, характеризующего геометрию дислокаций, накопленных на частицах (призматических петель, колец Орована, петель вторичного скольжения), Лр - расстояние между частицами, б - диаметр размера частицы.

Наиболее низкотемпературным диффузионным релаксационным процессом пластической деформации является процесс, связанный с миграцией межузельных атомов и их осаждением на дислокациях. В рассматриваемой модели ограничимся условиями, когда аннигиляция дислокаций и другие релаксационные процессы в дислокационной подсистеме осуществляются только за счет межузельных атомов. В этом случае интенсивность аннигиляции сдвигообразующих дислокаций с деформацией может быть представлена в виде [9]

а

- Pm Aldynn

2 p Gb

где G - модуль сдвига, Дт^ц

напряжение, избыточное над статическим сопротивле нием движению дислокаций [3,4,9], £ = 0.5 - фактор Смоллмена, п* - эффективное число дислокаций в скоплении [9], р - суммарная плотность дислокаций различного типа

Взаимодействие сдвигообразующих дислокаций с частицами порождает геометрически необходимые дислокации во всем их многообразии [5,7,9]. При плотностях дислокаций ниже критической р < рс это, главным образом, призматические петли ва- кансионного и межузельного типа, образование которых можно считать равновероятным [9].

Интенсивность аннигиляции вакансионных призматических петель в результате осаждения на них межузельных атомов может быть представлена в виде:

(a                        (v) л *

dpp ’        128 Рр ’ ATdynn                            , о

—=---------г-----L--,                    мл d а 3 < % > 8Ь р G где р^ - плотность дислокаций, входящих в вакансионные призматические петли.

При осаждении межузельных атомов на дислокациях, образующих межузельные петли, длина последних возрастает. Межузельные призматические петли в процессе деформации растут. Релаксационный рост межузельных петель может быть описан таким же образом, как и аналогичный ему процесс аннигиляции вакансионных призматических петель.

Интенсивность генерации межузельных призматических дислокаций складывается, таким образом, из двух слагаемых: 1) генерации таких дислокаций в результате скольжения сдвигообразующих дислокаций и 2) увеличения плотности геометрически необходимых дислокаций этого типа в результате релаксационного процесса - расши рения межузельных дислокационных петель в результате осаждения на них межузель ных атомов [9];

(1 (0 dpy da

2 g

<Х> 5     128 Р? Ax_dynn*

2Л2рЬ 3<х>бЬ р G где - плотность дислокаций, образующих межузельные петли.

Интенсивность аннигиляции межузельных призматических петель можно представить в виде [9]

’    .l>)i$-^-.              (6)

d«      3 р G

Таким образом, рассматриваемая модель эволюции дислокационной подсистемы деформируемого сплава с некогерентной упрочняющей фазой при докритических плотностях дислокаций может быть представлена в виде следующей системы дифференциальных уравнений:

Да О(рт»^2?Ь          Р Gb

. (v)                                 (v) А *

Фр _ < х > 5 128__Рр_ АзцуцЧ d« 2ЛрЬ 35b р G dp^ . _х - 6 _;    128 Pp ^T_dynn* 1б, у^РАтф^п*

d« 2ЛрЬ 3<%>5b р G 3 Р 2 р Gb

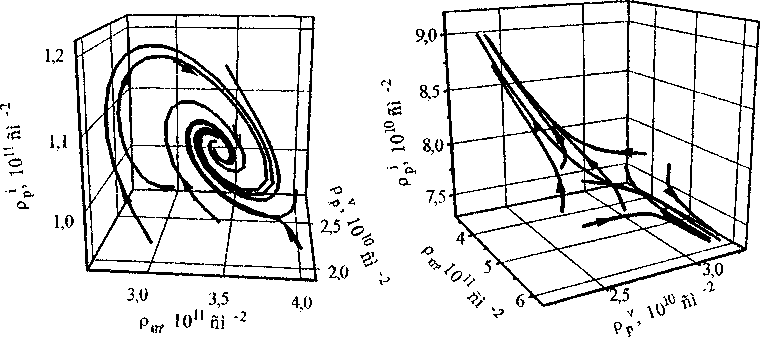
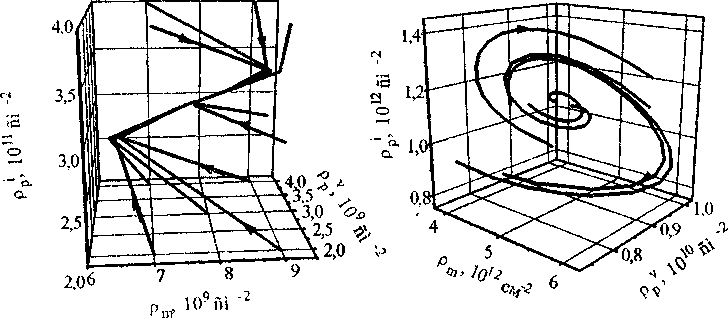
Проведено качественное исследование системы дифференциальных уравнений (7) в широком спектре значений параметров модели и интенсивности деформирующего воздействия (напряжения ATJy„) для дисперсно-упрочненных материалов на основе меди, алюминия и никеля. Показано, что в фазовом пространстве (р,^ рр', рр’) в широком интервале значений параметров существуют две стационарные точки, которые могут быть следующими (рис. 1): 1) одна устойчивая типа «фокус» или «узел», вторая неустойчивая типа «седло», 2) две неустойчивые типа «седло» или «фокус». Термины «фокус», «узел», «седло» традиционно применяются при анализе динамических систем на плоскости, но, как видно из рис. 1, аналогии вполне уместны.

Параметрический анализ структуры фазового пространства проведен для изменения значений параметров в пределах, соответствующих их физическому смыслу: F=2t5,7; п*=2-1б;   Ap=2-W4710'⁵ см; G=2-10% 10⁵ МПа; 5=10⁶ -ИО"⁵ см;

Tdyn= 100-2000 МПа.

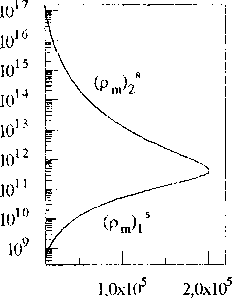
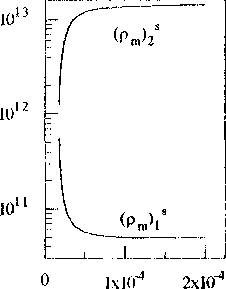
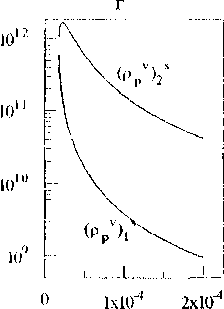
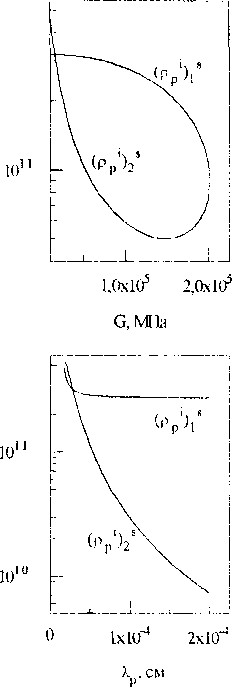
С ростом параметров Лр, Tdyn, п*, значение первой устойчивой стационарной плотности дислокаций р/1’ уменьшается, а второй ps<2i - увеличивается, вместе с этим увеличивается область между ps'n и р,<2) (рис.2). С увеличением параметра F, значение первой стационарной плотности дислокаций увеличивается, а второй - уменьшается. Влияние параметра 5 имеет нетривиальный характер, с ростом 5 система имеет несколько бифуркаций. Все смены типа стационарных состояний отмечены различными символами на кривых. На рис. 3 приведены стационарные значения плотности дислокаций различного типа, соответствующие приведенным на рис. 2 суммарным плотностям.

Проведены расчеты фазовых траекторий и соответствующие им зависимости суммарной плотности дислокаций и ее составляющих от степени деформации в широком спектре условий деформирования и начальных состояний Показано, что в зависимости от исходного дефектного состояния при данном воздействии возможна существенно различная эволюция дислокационной подсистемы. От случая с отжигом дефектов всех типов в процессе деформации, до случая, когда в процессе деформации наблюдается накопление дефектов всех типов, а также промежуточные режимы, при которых дефекты одних типов накапливаются, других типов - отжигаются. Наблюдаются также режимы с немонотонным изменением плотности дефектов.

в

г

Рис. 1. Локальные фазовые портреты при Ap=7T0"" см, G=105 МПа, 5=5-10'6 см, п*=2, Р=2: а) устойчивый фокус при т^Уп=Ю00 МПа (рт=3,43.10й см"2, ppv=2,25-1010 см'2, pp'=l,06-10n см'2); б) неустойчивое стационарное состояние при Tdyn=lOOO МПа (рт=4,975-10и см"2, ppv=2,8876 1O10 см'2, рр‘-—7,73-1010 см"2); в) устойчивый узел при Tdyn=2000 МПа и G=4-104 МПа (pm=7,91-109 см'2, ppv =3,122-Ю9 см'2, рр-3,153-1011 см'2); г) неустойчивый фокус при Tdyn =1800 МПа и 5=1,15-Ю"6 см (pm=4,981012 см'2, ppv =8,63-109 см'2, рр‘==1,15-1012 см'2)

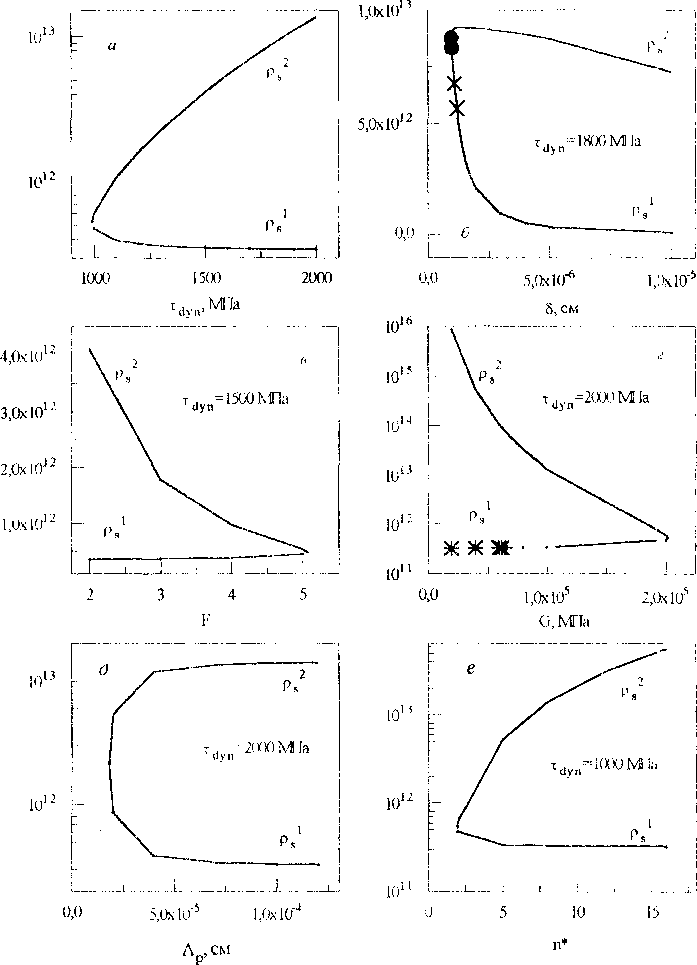
Рис. 2. Стационарные значения суммарной плотности дислокаций при различных значениях параметров , при n*=2, F=2, Лр=7*10'5 см, G=105 МПа, 5=5*10"6 см:---- устойчивое стационарное состояние (фокус);

------- - неустойчивое стационарное состояние, * - устойчивый узел; X - неустойчивый фокус

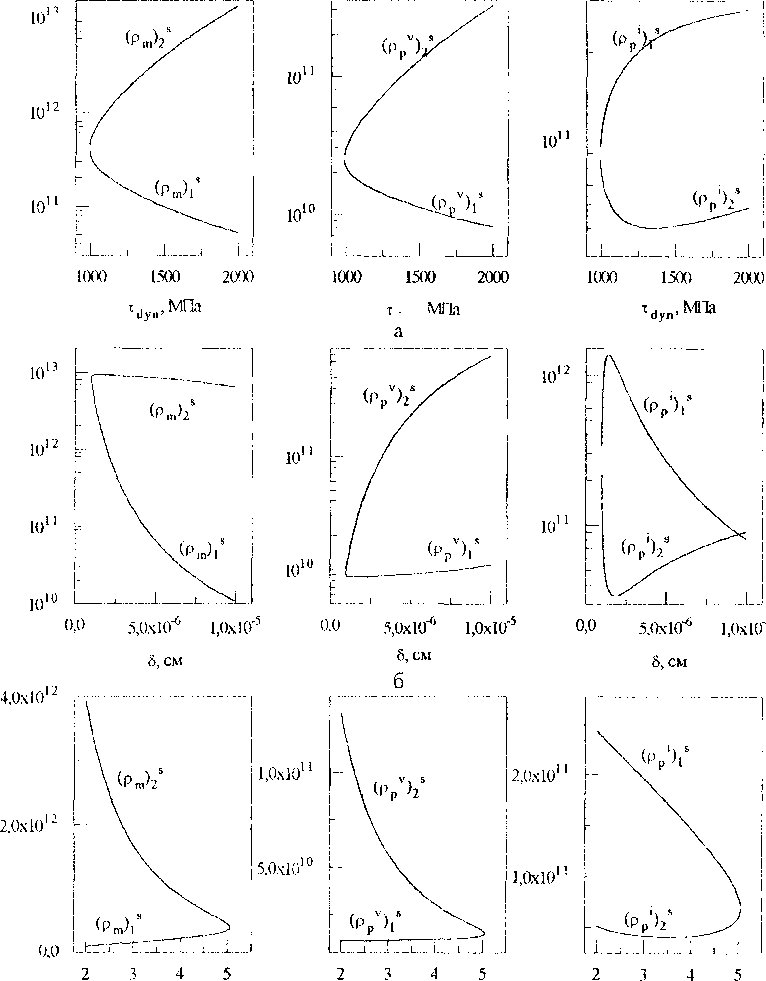
G, МПа

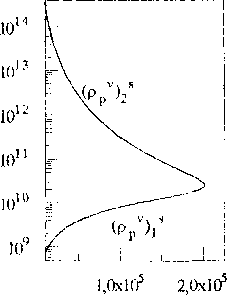
G МПа

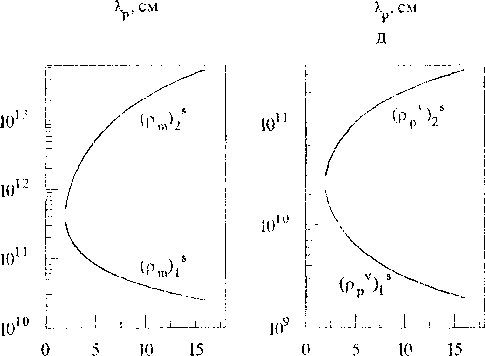
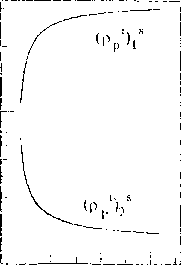
О 5 К) 15

е

Рис.З. Стационарные значения составляющих суммарной плотности дислокаций, соответствующие рис. 2, при различных значениях параметров (левый столбец рисунков соответствует сдвигообразующим дислокациям, средний - призматическим вакан-сионным петлям, правый - призматическим межузельным петлям).