Моделирование качки судна с подвешенным грузом

DOI:

Solovyov, A. A. et al. 2024. Modeling the motion of a ship with suspended cargo. Vestnik of MSTU, 27(4), pp. 591–597. (In Russ.) DOI:

Теоретический анализ качки – колебаний плавающего судна под воздействием внешних сил – представлен в работе известного ученого XVIII в. члена Петербургской Академии наук Леонарда Эйлера "Корабельная наука", изданной в России в 1749 г. Дальнейшее развитие теория качки судна получила в многочисленных трудах отечественных и зарубежных авторов (Собрание… , 1951; Семенов-Тян-Шанский и др., 1969; Благовещенский и др., 1975; Ремез, 1983; Нечаев, 1989; Чижиумов, 1999, 2010 ).

В настоящее время при совершенствовании теории качки возникла необходимость в строгой математической формулировке задачи о динамике судна на волнении и разработке надежных теоретических методов анализа соответствующих математических моделей. Известные решения для сравнительно простых нелинейных моделей, полученных с помощью бесконечных рядов, не всегда позволяют выявить из найденных выражений наиболее важные зависимости. Исключением являются только простейшие модели, описываемые линейными дифференциальными уравнениями, для которых решение может быть представлено в замкнутой форме, т. е. в виде аналитических формул. Особенность таких моделей состоит в том, что они описывают процессы, протекающие одинаково при различных воздействиях. С увеличением интенсивности воздействия изменения остаются количественными, новые качественные изменения не учитываются.

Область применения линейных моделей, основанных на использовании метацентрических формул в задачах качки и остойчивости, очень широка. Следует отметить, что методы анализа качки и остойчивости с помощью линейных моделей схожи и эффективны при использовании.

Важной задачей при изучении характера поведения судна в морских условиях является моделирование качки судна с находящимся на нем перемещающимся грузом (жидким, подвешенным). В немногих работах, посвященных этой проблеме ( Рахманин и др., 1997; Шауб, 2013; Buchner, 2002 ), рассматривается вопрос о влиянии жидкого груза на динамику судна.

В настоящей статье предложена линейная модель качки судна с подвешенным грузом на тихой воде и регулярном волнении.

Теоретические основы

Влияние подвешенного и жидкого грузов на остойчивость (рис. 1) заключается в создании кренящего момента за счет смещения их центра тяжести при наклонении судна. В теории начальной статической остойчивости действие этого момента учитывается уменьшением восстанавливающего момента посредством введения соответствующих поправок к начальной поперечной метацентрической высоте.

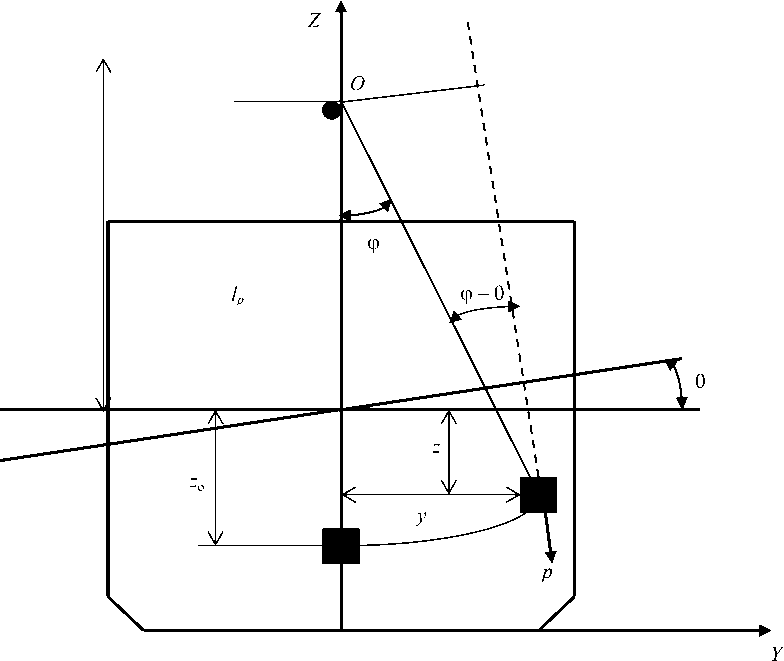
Рис. 1. Влияние подвешенного груза на остойчивость судна

Fig. 1. The influence of suspended load on the stability of a ship

Поправки вычисляются по формулам: – для подвешенного груза

⁵ h = - o'' •

– для жидкого груза, имеющего свободную поверхность:

5 h = - p p_p

Dх где р - вес груза; D - весовое водоизмещение судна; 1р - длина подвеса; рx - метацентрический радиус цистерны или танка.

Выражения (1) и (2) идентичны, что позволяет сделать вывод об идентичности влияния на остойчивость судна жидкого груза и подвешенного твердого тела, имеющего длину подвеса, равную р x . В дальнейшем в ходе анализа параметров качки будем рассматривать только подвешенный груз, так как для замены его на жидкий достаточно длину подвеса l_Р заменить на метацентрический радиус цистерны, величина которого может быть вычислена по формуле

ρ

x

=ж

p

где у - удельный вес жидкости; i x - момент инерции свободной поверхности относительно ее главной центральной оси.

При рассмотрении вопроса о влиянии подвешенного груза на параметры качки судна используем линейную теорию качки корабля. Уравнение бортовой качки на тихой воде представляет собой линейное дифференциальное уравнения второго порядка

( J_x + 5 J ) 0 + 2 N _e 0 + DhQ = 0,                                  (4)

где J_x - момент инерции массы судна относительно центральной продольной оси G_x ; 5 J x - присоединенный момент инерции массы воды; 2 N _э - постоянный коэффициент пропорциональности в выражении момента сил сопротивления качке; h – начальная поперечная метацентрическая высота.

Разделив уравнение (4) на множители при второй производной, получим е + 2ve0 + n;0 = 0,                                          (5)

где ve =

N θ     _,

J_x + 5J_X

ⁿ =

Dh

J_x + 8J_X ’

здесь v₀ - коэффициент затухания; n ₀ - частота собственных свободных колебаний судна.

Решение уравнения (5), написанное в тригонометрической форме, имеет вид

0 = e -

0₀соsю t + -( 0_О + v_e0_o ) sin® t , о

где 00 и 0О - начальные значения угла крена и угловой скорости; частота качки с учетом сил сопротивления равна

® = № ^{- v} 0 .

Уравнение (8) определяет гармоническое затухающее колебательное движение с постоянным периодом 2π

T = — и переменной амплитудой 0_О e  .

ω

При составлении уравнения бортовой качки судна на тихой воде с учетом наличия подвешенного груза в уравнение (4) необходимо добавить момент инерции и момент силы веса, создаваемый этим грузом. Поэтому момент J_x будем рассматривать как сумму двух составляющих:

Jx = Jxo + Jxp, где Jxo – момент инерции массы судна без подвешенного груза; Jxp – момент инерции подвешенного груза.

Момент инерции J_xp также состоит из суммы двух составляющих: первая зависит от расположения груза относительно оси наклонения при конкретном угле отклонения от вертикали ф и является величиной переменной, вторая – собственный момент инерции массы груза:

Т _ Р(        ,Р¹+ ⁺ ' У

Jxp = ДzФ + yФ ’'         , gg где z и у - координаты груза при заданном угле ф; lz и ly - линейные размеры груза.

Поскольку второе слагаемое является величиной постоянной, то его можно объединить с моментом инерции судна J x o .

Как видно из рис. 1, координаты центра тяжести груза при произвольном угле ф могут быть вычислены по следующим формулам:

z ф = z о - ( l p - I p cos ф ) “ z o ,

У ф = l_P sin ф ~ l p Ф, где l_p - длина подвеса; ф - угол отклонения линии подвеса от вертикали.

С учетом полученных зависимостей общий момент инерции массы судна будет вычисляться по формуле

^Jx = ^Jx o + p [ z 02 + ( l p ф ) ² ] .

Момент силы веса подвешенного груза, противоположный по знаку восстанавливающему моменту, вычисляется так:

M_p = Pl p sin ( ф ^{- 0} ) ~ Pl p ( ф ^{- 0} ) .

С учетом выражений (10) и (11) уравнение качки судна на тихой воде с подвешенным грузом имеет вид

Jxo + p[z2 +(lpф)2] + JJ0 + 2N00 + Dh0-plp (ф-0) = 0.(12)

I      gL

Раскрывая скобки и группируя слагаемые, содержащие 0 , получим выражение

| Jxo + p [ z2 +(lp ф )2 ] + J j 0 + 2 N00 + (Dh + plp )0 - plp ф = 0.(13)

Разделив на множитель при второй производной, получим

0 + 2ve0 + ne20 - m0 ф = 0,(14)

где

Nθ

^Jx o ⁺ p ^[ z 2 ⁺ ( l p ф )^{2 ] +} J x ^g

n

Dh + pl_p

Jxo + p [z2 +(lpф)2 ] + JX plp

^Jx o ⁺ p ^[ z ^{2 +} ( l p ф ) ² ] ⁺ J x

Из формул (15) и (16) видно, что коэффициент затухания v₀ , частота собственных колебаний n ₀ и зависящий от них период качки Т являются переменными величинами, так как зависят от угла ф , значение которого может быть определено из решения дифференциального уравнения качания подвешенного груза

J o ф + N ф ф + pl p ( ф - 0 ) = 0, (18)

p ₂

где Jo = — l- момент инерции подвешенного груза относительно точки подвеса; Nф - постоянный gp коэффициент пропорциональности в выражении момента сил сопротивления качанию груза.

Таким образом, для расчета параметров качки судна с подвешенным грузом необходимо решение системы двух дифференциальных уравнений (14) и (18), реализовать которое можно только численными методами.

Бортовая качка судна на регулярном волнении описывается уравнением

(Jx + 8 Jx) 0 + 2N0 + Dh(0 - a) = 0,(19)

где a - текущий угол волнового склона.

После преобразования уравнение будет иметь вид

(Jx + 8 Jx) 0 + 2 N 0 + Dh0 = Dha.(20)

Угол волнового склона в данном месте и данный момент времени вычисляется по формуле a = a.sinot,(21)

2πr где а = N0 К0^а ; а =--в; ао - наибольший угол волнового склона; ат - исправленный угол mθв θTo      o      λ волнового склона; ^0в, ^0T - поправочные коэффициенты, учитывающие конечные размеры суда; 2rв -высота волны; X - длина волны; а - частота волны.

С учетом приведенных выражений (21), уравнение (20) принимает следующий вид:

( J_x + 8 J_x ) e + 2 N 0 + Dh0 = а„ Dh sin с t .                           (22)

Разделив все члены уравнения (22) на коэффициент при второй производной, приводим его к виду

0 + 2v_e0 + n 2 0 = a_mn 2 sin c t .

Общий интеграл уравнения (23) имеет вид

0 = e ^vt ( C cos nt + C ₂ sin nt ) + 0,

где θ – частное решение уравнения, которое определяет вынужденные колебания и находится по формуле

0 = 0_m sin ( о t - 8 ) ,

здесь tg8 = 4^, n e - о

0 m =            ."         .

7( n ^{2 - о}2 ) ^{+ 4v}0^o0

Итак, общий интеграл дифференциального уравнения бортовой качки в абсолютных координатах рассчитывается как

0 = e“vt | 0O coswt + — (0O + ve0o)sinwt | + 0m sin(оt-8).(28)

(           о

Для составления уравнения, описывающего бортовую качку судна с учетом подвешенного груза, уравнение (20) необходимо дополнить моментом веса подвешенного груза и моментом инерции его массы; после преобразований данное уравнение приводится к следующему виду:

• | Jxo + p [ z2 + (lp Ф )2 ] + 8Jx 10 + 2 N00 + (Dh + plp )0 - plp Ф = Dha.(29)

Разделив все члены уравнения (29) на коэффициент при второй производной и учитывая выражения (21), получим формулу

0 + 2ve0 + n20 - meф = amn2 sin оt,(30)

где n ² =----------------------; коэффициенты v₀, n 2 и m₀ вычисляются по выражениям (15)-(17)

J.. + p [ z2 + (lp Ф )21+8J, g соответственно.

Моменты инерции J x o обычно находятся по приближенным формулам. Из опубликованных в технической литературе приближенных формул, дающих более точные результаты, наиболее часто рекомендуют:

._T D (B ² а²   я² ^        _D

• 1)    формулу Шиманского J =—--1--, где В - ширина судна; Н - высота борта;

^{x o}    g ^ 11,48   12 )

а - коэффициент полноты площади ватерлинии; 5 - коэффициент общей полноты. Формула выведена в предположении, что корпус судна представляет сплошной параболический цилиндр;

2) формулу Дуайера

■ '• o = 1 D ⁽ B + ⁴ - ■),

где z g – аппликата центра тяжести судна. Формула

предполагает, что корпус судна представляет собой сплошной прямоугольный параллелепипед шириной В и высотой 2 z_g ;

• 3)    формулу Павленко J_xo = —B2 ² + н 2 V

x o    _{16 g}

D 2

• 4)    эмпирическую формулу J_{x о} + 8 J_x = — р_х , где р _x - приведенный радиус инерции судна с учетом ^g

присоединенной массы воды р _ч = cB . Эмпирический коэффициент с вычисляется по рекомендованной IMO и Российским морским регистром судоходства формуле c = 0,373 + 0,023 B / d - 0,043 L^ _z/100, где L_wl – длина судна по ватерлинии.

Момент инерции присоединенной массы определяется по формуле

8 Л = — (В ² + 4 d ²) —.

• ^x 12 g            10δ

Результаты и обсуждение

Уравнения (4) и (22) описывают качку судна на тихой воде и на регулярном волнении без учета момента, создаваемого подвешенным грузом; системы уравнений (14), (18) и (29), (18) – с учетом влияния подвешенного груза на кренящий момент и момент инерции суда.

Для вычислений была использована математическая модель судна водоизмещением 1 000 т, длиной 50 м, шириной 9 м; осадка 3,68 м; начальная поперечная метацентрическая высота 1,0 м.

Инклинограммы качки судна на тихой воде, полученные посредством решения уравнения (4) и системы уравнений (14), (18), показывают классические периодические затухающие колебания (рис. 2) и выраженную

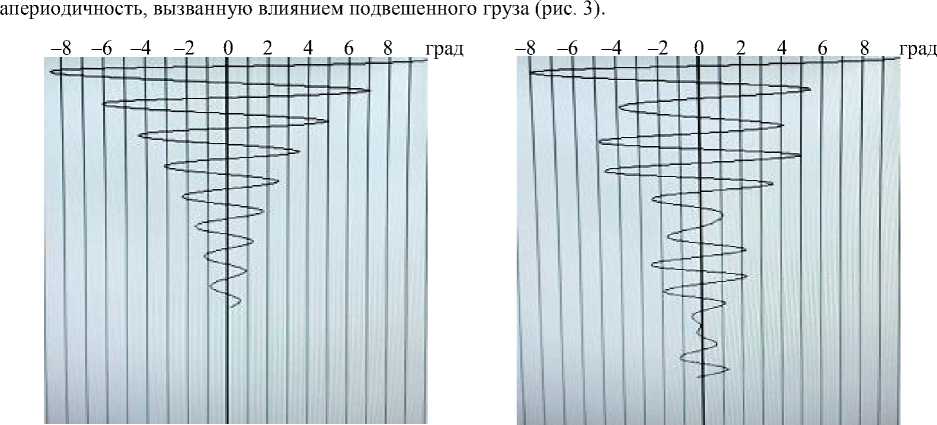
Рис. 2. Качка судна без подвешенного груза на тихой воде

Fig. 2. Rolling of a ship without suspended cargo on calm water

Рис. 3. Качка судна с подвешенным грузом на тихой воде

Fig. 3. Rolling of a ship with suspended cargo on calm water

Инклинограммы качки судна на регулярном волнении получены в результате решения уравнения (22) и системы уравнений (29), (18). Качка судна на регулярном волнении имеет постоянный период (рис. 4),

Рис. 4. Качка судна без подвешенного груза на волнении

Fig. 4. Rolling of a ship without suspended cargo in rough seas

Рис. 5. Качка судна с подвешенным грузом на волнении

Fig. 5. Rolling of a ship with suspended cargo in rough seas

Заключение

В результате исследования получены линейные дифференциальные уравнения качки судна с подвешенным грузом на тихой воде и регулярном волнении. Наличие на судне подвешенного груза значительно изменяет параметры качки за счет возникновения кренящего и переменного моментов инерции судна.

Предложенные математические методы позволяют моделировать качку на любом регулярном волнении с учетом произвольных значений поперечной метацентрической высоты, веса груза и длины подвеса.