Моделирование качки волномерного буя

Волномерные буи (ВБ) являются наиболее распространенным прибором, используемым для измерения характеристик морского волнения. В зависимости от назначения эти приборы позволяют определять статистические и спектральные характеристики волн, параметры одномерного и двухмерного спектров трехмерного волнения, а также выполняют экспресс-анализ записанной реализации. Методы измерения, используемые в этих приборах, обычно основаны на применении датчиков давления и акселерометров для измерения ординат возвышения волн, а также различных датчиков углов для измерения углов волнового склона.

При колебаниях на поверхности волны буй совершает сложные пространственные движения, обусловленные влиянием волновых и ветровых возмущений. Очевидно, что погрешность измерений характеристик волнения непосредственно зависит от того, насколько точно буй отслеживает профиль волны. В общем случае погрешности измерения ординат волн, обусловленные гидродинамическими свойствами буя, можно разделить на три группы. Первую и вторую группы составляют погрешности, обусловленные линейными и угловыми перемещениями буя относительно поверхности волны, третью — погрешности, обусловленные линейными смещениями буя относительно географической точки измерений. Указанные погрешности впрямую зависят от массо-габаритных характеристик прибора, выбор которых при проектировании ВБ необходимо производить с учетом минимизации этих погрешностей.

СИСТЕМЫ КООРДИНАТ И ПРИНЯТЫЕ ДОПУЩЕНИЯ

Рассмотрим подробнее пространственные движения цилиндрического буя. Определим систему координат, связанную с буем, как X,Y,Z и систему координат взволнованной поверхности моря как ^ , П - С - причем оси С и Z направлены вниз (рис.1).

Рис. 1. Системы координат

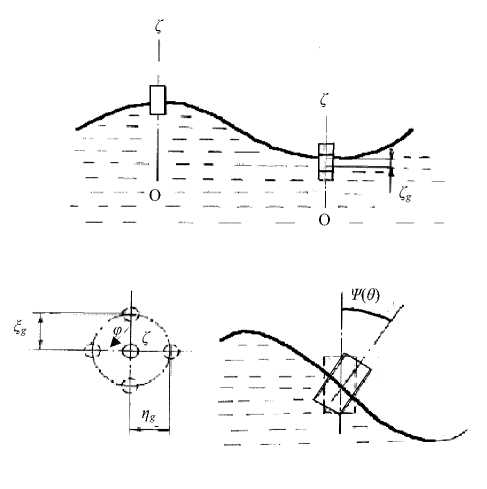
Рис. 2. Пространственные движения буя под воздействием волн

Z P — координата центра тяжести (ЦТ), Z g , Z g , n g — перемещение связанной с телом системы координат ( XYZ) относительно неподвижной ( ZZn ).

При подъеме и спуске буя со склонов волн он, как любое плавающее тело с шестью степенями свободы, совершает угловые колебания 6 относительно оси Ос в плоскости O n Z (рис-2), угловые колебания у в плоскости О Е С относительно оси O n , колебания по углу ф в плоскости О пЕ относительно оси Оζ , имеет вертикальную качку ζ g , а также совершает линейные продольные n g и поперечные E g колебания в горизонтальной плоскости.

В связи с тем что корпуса буев, как правило, симметричны относительно оси О ₁ Z, в дальнейшем будем рассматривать лишь углы 6 и колебания n g , т.к. рассуждения относительно углов щ и колебаний ^ g будут аналогичными. Составим дифференциальные уравнения движения буя, используя гидродинамическую теорию качки судна.

Для этого примем следующие допущения.

• 1.    Движение жидкости считается потенциаль-

• ным, что позволяет определить скорость движения любой частицы воды через производные по направлению, т.е.

• 2.    Движение буя в воде считается безвихревым.

• 3.    Жидкость считается тяжелой и несжимаемой.

• 4.    При определении гидродинамических коэффициентов используется гипотеза плоского обтекания, а трехмерность обтекания учитывается путем введения поправок.

• 5.    Гидромеханические силы разделяются на ряд составляющих.

V X

ЭФ v ЭФ v ЭФ

ЭХ ’ Y "дУ ’ Z "Э2 ’ где Ф — потенциал скорости.

К составляющим гидромеханических сил относятся следующие.

— Инерционные силы, возникающие вследствие изменения кинетической энергии жидкости, вызываемого качающимся буем на тихой воде. Эти силы пропорциональны ускорениям качки буя в первой степени. В выражениях этих сил или их моментов множители при соответствующих ускорениях называются присоединенными массами и имеют размерность масс, размерность моментов инерции масс и размерность статических моментов масс.

— Восстанавливающие, или гидростатические, силы, возникающие как реакция воды на перемещение буя и стремящиеся вернуть буй в положение, совпадающее с положением его на тихой воде. Эти силы распределены по смоченной поверхности буя.

— Силы сопротивления, или демпфирующие, силы, возникающие вследствие непрерывного рассеивания энергии качающегося буя. Эти силы, в свою очередь, можно подразделить на силы волновой и силы вязкостной природы. Первые обусловлены гравитационными свойствами воды и определяются непрерывным расходованием энергии на поддержание системы волн, распространяющихся во все стороны от качающегося буя. Силы волнового сопротивления при качке пропорциональны первой степени скорости колебаний. Эти силы, так же как и инерционные гидродинамические силы, обусловлены теми возмущениями, которые вносятся в спокойную жидкость вынужденной качкой буя. Вторые обусловлены вязкостью воды и определяются как сумма сопротивления трения и сопротивления формы, связанного с вихреобразованием.

— Возмущающие силы, возникающие вследствие непрерывной передачи бую части энергии волнующейся жидкости. Возмущающие силы делятся на две части: главную и дополнительную — дифракционную. Главная часть возмущающих сил представляет собой результирующую гидродинамических давлений, которые распределены по смоченной в данный момент поверхности буя. Эта часть сил есть следствие изменения набегающей волной формы погруженной части буя по сравнению с формой, соответствующей тихой воде, и отличия поля давлений в неискаженной буем волне от поля гидростатических давлений. Дополнительная, или как ее называют дифракционная, часть возмущающих сил представляет собой результирующую гидродинамических давлений, обусловленных возникновением отраженных волн.

Инерционные и восстанавливающие силы относятся к числу консервативных сил, и, следовательно, работа за период каждой из них порознь равна нулю.

Силы сопротивления относятся к числу диссипативных сил, и их работа (по отношению к бую) всегда отрицательна.

Возмущающие силы всегда явно зависят от времени и от элементов набегающих волн.

Восстанавливающие силы и главная часть возмущающих сил характеризуют прямое воздействие на буй окружающей его воды без учета движения жидкости, вызванного движением буя.

Инерционные, демпфирующие силы и дифракционная часть возмущающих сил являются следствием тех изменений в движении жидкости, которые обусловлены присутствием в ней качающегося буя. Таким образом, эти силы учитывают вторичное явление, т.е. обратное воздействие буя на жидкость.

МАТЕМАТИЧЕСКОЕ НЕЛИНЕЙНОЕ МОДЕЛИРОВАНИЕ КАЧКИ

Давление в жидкости при неустановившемся ее движении определяется интегралом Лагранжа—

Коши:

ЭФ 1 з

P - Р о = yZ + р — + - p V ²,        (1)

d t 2

где Р - Р _о— избыточное давление, Р ₀ — атмосферное давление, Р — давление жидкости, р — плотность воды, V — скорость абсолютного движения жидкости, у = p g, Ф — потенциал скорости, причем Ф = Ф _W + Ф д + Ф _Ид . Здесь Ф w — потенциал скорости, обусловленный свободными набегающими волнами, Ф д — потенциал скорости, обусловленный присутствием неподвижного буя в жидкости, Ф _Ид — потенциал скорости, который возникает от качки буя на тихой воде.

Первый член правой части уравнения (1) определяет гидростатическое давление, второй и третий члены учитывают давление, обусловленное набегающей и дифрагированной волнами. С помощью интеграла Лагранжа—Коши можно определить давление на элементарном участке поверхности погруженной части буя. Для определения силы, действующей на корпус буя, следует проинтегрировать элементарные давления по всей смоченной поверхности:

F = J(Р-Po)dS , St где St — мгновенная площадь смоченной поверхности буя, которая изменяется во времени.

Силы и моменты сил, действующие на движущийся буй при его движении в плоскости Z OZ, можно описать системой трех уравнений

F ^ = J ( Р - P о )d S cos( n Z ),

S t                    ^

- F = J ( Р - P о )d S cos( n Z ),

\             A        A

M _n = J ( Р - Р _о)( X cos( nZ ) - Z cos( nX ))d S .

S t

Здесь обозначениям nZ , nn , nZ , nZ , nX соответствуют углы между нормалью к элементарному участку смоченной поверхности корпуса буя (на рис. 3 показан в форме конуса) и соответствующими осями координат, а отрицательный знак A перед слагаемым Z cos (nX) в третьем уравнении системы вызван тем, что положительный момент соответствует движению по часовой стрелке.

В соответствии с принципом Д' Аламбера пространственное движение буя может быть описано системой уравнений

( m + Xz ) Z = F z ,

-(m + Xz )Z = Fz , (2) (JY + Xn )6 = MY, где m — масса буя; Xz, X^ — присоединенные массы при колебаниях буя по соответствующим осям; Хп — присоединенный момент инерции; 6 — угол колебаний (рис. 3); JY — момент инерции относительно оси 01Y.

Для удобства вычислений разделим гидродинамические силы F z и F z , а также момент M Y на ряд составляющих, как было указано ранее:

FZ(Z) (Мп) =F1+F2+F3+F4, где F1 — гидростатическая сила (или момент), которая определяется путем интегрирования гидростатического давления по смоченной поверхности; F2 — главная часть возмущающих сил, определяемая интегрированием волнового давления по смоченной поверхности при условии, что буй не вносит искажений в волновое поле; F3 — дифракционная составляющая волнового поля, обусловленная искажениями волнового поля от присутствия буя; F4 — демпфирующая составляющая, обусловленная силой сопротивления при качке на тихой воде.

Для выполнения расчетов по выражению (2) необходимо иметь значения присоединенных масс и момента инерции буя. Значения присоединенного момента инерции при угловых колебаниях буя могут быть получены из выражения to о2

Dh

Х п + J y ’

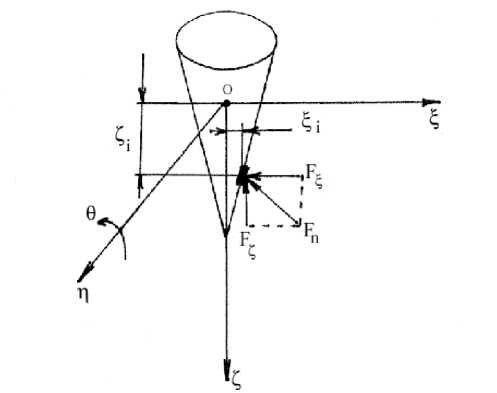
Рис. 3. Силы, действующие на буй где h — метацентрическая высота, D = mg — вес

В том случае, если масса буя равномерно рас- пределена по его объему, а угловые колебания буя в воде происходят относительно точки О (рис. 4), лежащей в центре сечения ватерлинии ВЛ, то мо- жет быть получено выражение для момента инер- ции цилиндрического буя. Для этого разобьем его корпус на элементарные объемы, каждый из кото- рых лежит между сечениями, параллельными плоскости ватерлинии, и имеет высоту dZ. Тогда выражение для элементарной массы, соответствующей этому объему, будет pnR 2dZ = dm , а элементарный момент инерции определится как d J y = dmZ2.

Момент инерции буя в целом определится из выражения

T

J y = I'd J y = Pn R ^!1 ( r ° - h 03 ) .

h 0                     ³

Заметим, что значение h₀ необходимо брать с учетом знака. В связи с тем что ось Z направлена вниз (рис. 4), значение h 0 всегда будет отрицательным. Для определения метацентрической высоты необходимо рассчитать момент М восстанавливающих сил на тихой воде. На рис. 5 представлен буй в наклоненном состоянии. При его отклонении от вертикали на угол 6 объем V 1 входит в воду, а объем V 2 выходит из нее. Выделим элементарный объем dV из V₁ . Толщину этого объема по оси X обозначим dX , высота Z_t = X i tg 6 . Для определения Y_i используем уравнение окружности радиуса R с центром в начале координат: X ² + Y i ² = R ². Откуда получим Y i = ^R ² - X² . Тогда выражение для элементарного объема будет иметь вид:

dV = 2V R 2 - X²X tg 6 d X .        (4)

Момент от этого элементарного объема равен

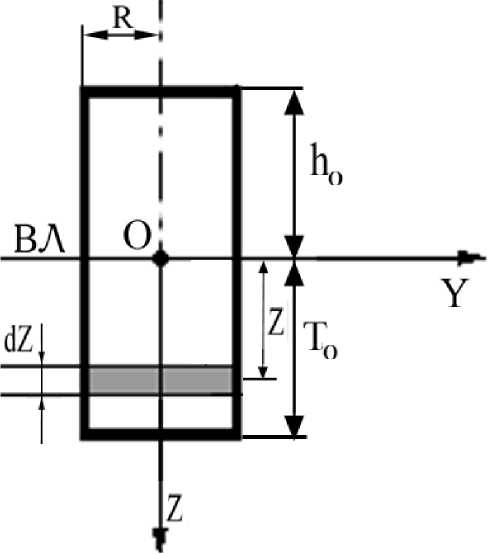
Рис. 4. Разбиение цилиндрического буя на элементарные отсеки. ВЛ — ватерлиния.

При определении момента, возникающего при наклонении буя, следует рассматривать не только объем V₁ , но и объем V₂ (рис. 5). В связи с тем что V 2 = V 1 , значение выражения (7) следует удвоить, кроме того, учитывая малость углов 6 , следует принять tg 6 = 6 , тогда выражение для момента примет вид:

M = 4 p g nR⁴6 .

Значение метацентрической высоты можно определить из формулы:

M h =---

D 6

.

dM = p gX i d V .                 (5)

Подставляя выражения (8) и (9) в (3), получим:

Подставляя (4) в (5), получим выражение для момента, обусловленного объемом V 1 :

R

MV = pg J 2 V R 2 - X2X(2 tg 6dX(.(6)

Решение интеграла определится как

МV1 = 1 PgnR 4tg6 .

_ю 2 = 0^5 p gR^ 0" А , + J y

.

Окончательно выражение для присоединенного момента инерции примет вид:

Ап = °'785ppgR4 - Jy.(10)

^ю °

Таким образом, зная частоту свободных колебаний буя в воде и его геометрические размеры

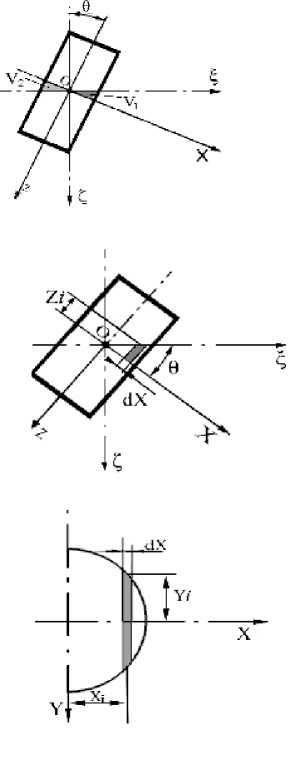
Рис. 5. Определение элементарных объемов для расчета момента восстанавливающих сил

где S m = S Ml — приращение момента инерции буя, соответствующее увеличению угла его отклонения Se от вертикали; S M — приращение массы; l — расстояние между осью качания буя и местом установки массы; коэффициент 57.3 учитывает перевод угла в радианы.

С целью определения значений а и J y по формулам (11) и (12) был произведен эксперимент по определению значений S m , Se и Т . Для этого на корпусе буя с помощью хомута была закреплена штанга с ножевыми опорами 1 (рис. 6) и площадкой 2 для установки грузов. Грузы массой 0.1 и 0.2 кг попеременно устанавливались в точки а, б, в, г , расположенные друг относительно друга на расстоянии 0.1 м. При этом точки б и в отстояли от оси качания также на 0.1 м. Угол наклона буя определялся с помощью оптического квадранта. Для буя массой 27 кг и диаметром 0.34 м значение времени Т составило 2.1 с, а J y = 0.64 кг∙м².

Для определения значения присоединенного момента инерции и коэффициента сопротивления был выполнен эксперимент по записи свободных угловых колебаний указанного буя в опытовом бассейне на тихой воде. Запись угловых колебаний производилась с помощью индикаторной гировертикали ДК-14. Частота собственных колебаний составила 3.59 с -1 . Значение Х_п было рассчитано по формуле (10) и оказалось равным 0.356 кг∙м², что составило 55% от значения момента инерции в воздухе. Значение Х ^ определялось по методике, изложенной в [1], и составило 5.23 кг.

Для определения коэффициента сопротивления W В при квадратичном законе демпфирования для бортовых колебаний была использована методика, приведенная в [2]. Значение коэффициента сопротивления рассчитывалось из выражения:

можно рассчитать значения присоединенного момента инерции. В том случае если масса буя неравномерно распределена по его поверхности, то для определения J y можно воспользоваться записями его собственных колебаний в воздухе. При этом расчет момента инерции буя в воздухе следует производить на основе выражения:

Wb=0.85®c rKw, где KW — квадратичный коэффициент сопротивления, юС — частота собственных колебаний, r — амплитуда качки.

Выражение для K_W имеет вид:

K w =C w ( J y +Х- ц ) .

Jy

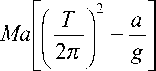
Здесь J_y — момент инерции буя в воздухе, Х _п — присоединенный момент инерции, С W — квадратичный коэффициент сопротивления (1/град.).

Здесь М — масса буя (кг), Т — период собственных колебаний буя в воздухе (с), а — расстояние точки подвеса буя от центра масс (плечо подвеса) (м).

Значение а можно определить из выражения

При этом

_г _ 3A A n

CW =    2 , ncc

A A n = A n cp ^- A n + 1ср --

уменьшение средней амплитуды за два периода ( n

и n+ 1), A_{n cc}

57.3У SmSe a =--^—о—, м £ seг

А + А .

n cp       n + 1ср

— средняя для двух

периодов амплитуда.

Зависимость коэффициента сопротивления от угловой скорости колебаний представлена на рис. 7.

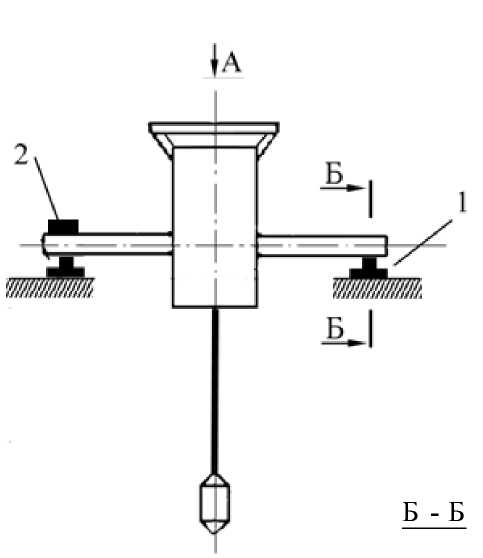
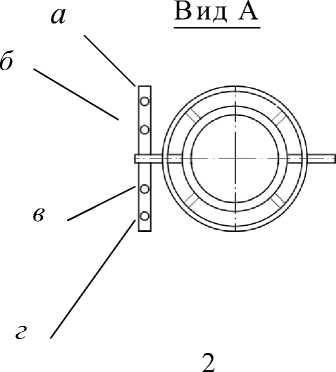
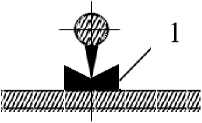
Рис. 6. Схема эксперимента по определению значений δm, δθ и T

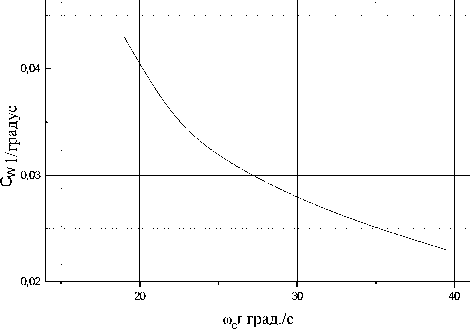
Рис. 7. Зависимость коэффициента сопротивления от скорости угловых колебаний буя диаметром 0.34 м и массой 27 кг

Аналогичным образом были получены коэффициенты сопротивления для вертикальных колебаний указанного буя, которые представлены на рис. 8, и коэффициент присоединенной массы λ ζ = 13.8 кг.

На основе предложенной математической модели были произведены расчеты качки буя с указанными ранее характеристиками. Для выполнения расчетов разработана программа, позволяющая решать систему дифференциальных уравнений методом Рунге—Кутта.

Результаты расчета АЧХ качки представлены на рис. 9 и 10.

С целью сравнения результатов расчета с экспериментальными данными в опытовом бассейне ЦНИИ им. акад. А.Н. Крылова был произведен эксперимент по определению АЧХ вертикальной и угловой качек буев. С помощью волнопродуктора задавалась волна с необходимой высотой и периодом, характеристики которой контролировались по струнному волнографу, закрепленному на

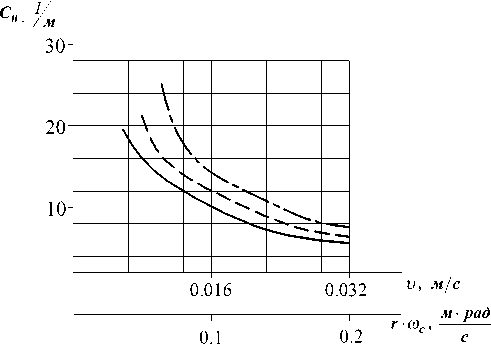
Рис. 8. Экспериментальная зависимость квадратичного коэффициента сопротивления от скорости колебаний буя ∅ 0.34 м при массе буя 27 кг ( ), 29 кг ( ), 36 кг ( )

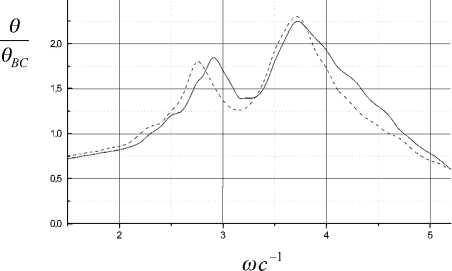
Рис. 10. Сравнение экспериментально полученной АЧХ бортовых колебаний буя 0.34 м и массой 27 кг ( ) с характеристикой, рассчитанной на основе численного решениия уравнений ( ). Характеристики даны при крутизне волны 1/40

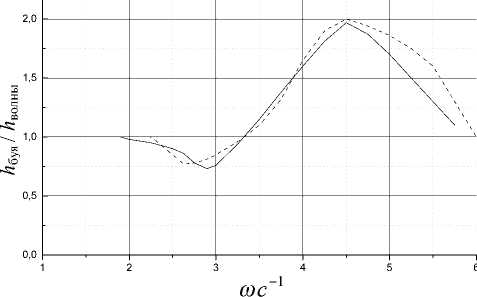
Рис. 9. Сравнение расчетной АЧХ вертикальной качки буя ∅ 0.34 м массой 27 кг ( ) с экспериментальной характеристикой ( ). Характеристики даны при крутизне волны 1/40

рассчитанными кривыми (рис. 9, 10), что позволяет говорить о хорошем качестве разработанной математической модели. На рис. 10 θ ВС обозначает угол волнового склона. Заметим, что диапазон измеренных характеристик ограничивался возможностями опытового бассейна. Следует отметить и то, что расчет угловых колебаний производился для цилиндрического буя со значительной осадкой, который недостаточно хорошо отслеживает углы волнового склона и предназначен для измерения только ординат профиля волн.