Моделирование каскадов атомных смещений в бинарном сплаве Fe-1.8ат.%Ni методом молекулярной динамики

Малолегированные стали с содержанием никеля 1,0-1,9 % типа 15Х2НМФАА используются для изготовления корпусов реакторов типа ВВЭР-1000. Планируется их применение в проектируемых сейчас реакторах ВВЭР-1200 (АЭС 2006/2009) ВВЭР-1500. В результате многочисленных исследований показано, что повышение концентрации никеля значительно понижает радиационную стойкость малолегированных сталей, однако физическая сущность процессов, приводящих изменению свойств, в настоящее время изучена недостаточно.

Одним из общепринятых и широко используемых методов моделирования первичного радиационного повреждения конструкционных материалов ядерных и термоядерных установок является метод молекулярной динамики. К настоящему времени различными группами исследователей по всему миру проведено большое количество таких исследований применительно к различным материалам. Особенно много данных получено для чистого a-Fe с использованием различных потенциалов межатомного взаимодействия. Моделирование каскадов в сплавах также широко выполняется, хотя для многокомпонентных систем сохраняется проблема подготовки надежных потенциалов. В последние годы опубликовано достаточно большое количество работ, посвященных как подготовке соответствующих потенциалов межатомного взаимодействия, так и проведению такого моделирования (см., например работы [1–6]).

Тихончев Михаил Юрьевич, кандидат физико-математических наук, начальник лаборатории моделирования поведения неорганических материалов.

Данная работа посвящена моделированию каскадов атомных смещений для сплава Fe-1.8ат.%Ni методом молекулярной динамики с целью определения ряда параметров первичной радиационной повреждаемости такого сплава с учетом процессов рекомбинации и кластеризации точечных дефектов в каскадах смещений. Полученные результаты уточняют и дополняют соответствующие результаты, полученные нами ранее [7].

2.    ПОТЕНЦИАЛЫ МЕЖАТОМНОГО ВЗАИМОДЕЙСТВИЯ

Для железа в настоящем исследовании для a -Fe мы использовали многотельный потенциал типа Финниса-Синклeра из работы Акланда, Бэкона и др. [8]. Для описания взаимодействий вида Ni-Ni и Fe-Ni мы использовали потенциал того же типа, предложенный Хепберном, Акландом и Олссоном в их недавней работе [5]. Причем разбиение парных частей соответствующих потенциалов проведено по формулам (3-6), т.е. так же, как это сделано для взаимодействий Fe-Fe. Отметим два момента. Во-первых, поскольку используемые потенциалы относятся к типу потенциалов Финниса-Синклeра, смешанные взаимодействия Fe-Ni описываются заданием соответствующих функций ф (r) и у (r) (в методе погруженного атома смешанные взаимодействия описываются только соответствующей парной частью ф (r)). Во-вторых, используемые Ni-Ni и Fe-Ni потенциалы предназначены только для описания никеля как примеси замещения в матрице a -Fe с небольшой (до нескольких процентов) концентрацией никеля.

3.    МОДЕЛИРОВАНИЕ КАСКАДОВ СМЕЩЕНИЙ

Для моделирования каскадов атомных смещений и оценки числа “выживших” дефектов задавались ОЦК кристаллиты “чистого” a-Fe и бинарного сплава Fe-1.8ат.%Ni, содержащие до = 800000 атомов. При этом атомы Ni в бинарном сплаве задавались как атомы замещения, и расположение атомов разных типов носило случайный характер, т.е., каждому атому кристаллита с вероятностью p=0.982 приписывался тип Fe и с вероятностью (1–p) – Ni. При расчётах использовались “периодические” граничные условия. Поэтому, чтобы избежать цикличности возмущений вдоль плотноупакованного направления <111>, кристаллиты задавали в форме прямоугольного параллелепипеда, но не куба. Моделирование проводилось при начальной температуре кристаллита T = 600 K для шести различных энергий ПВА (Е_ПВА): 0.1, 0.5, 1, 2, 5, 10, 15, 20 и 30 кэВ. Начальную температуру обеспечивали путем задания начальных скоростей атомам кристаллита с последующим молекулярно динамическим моделированием NPT-ансамбля с баростатом и термостатом Берендсена для нулевого давления и температуры 600 К, соответственно, в течении 1 пс с шагом по времени 1 фс. Затем, фиксированному атому (ПВА) релаксированного кристаллита (это мог быть как атом Fe так и Ni) придавали импульс в некотором направлении. Для каждой энергии ПВА моделировали каскад для восемнадцати различных направлений, которые выбирались путем моделирования случайного изотропного вектора.

В ходе моделирования каскадов никакие алгоритмы сброса кинетической энергии для имитации “остывания” кристаллита не использовались. Рост температуры кристаллита составил от = 16 К для Е ПВА =0.1 кэВ до = 145 К для Е ПВА =30 кэВ. Расчеты проводились с неравномерным шагом по времени, который выбирался так, чтобы он не превосходил 10^-3 пс, и чтобы за один шаг по времени атом с максимальной кинетической энергией смещался не более чем на 0.02 Е.

Моделируемое время развития каскада подбиралось так, чтобы обеспечить моделирование всего процесса образования и релаксации точечных дефектов в каскаде вплоть до его затухания.

При моделировании каскада смещений периодически проводился анализ кристаллита, подсчитывалось число точечных дефектов, переживших рекомбинацию в каскаде, и определялось среднее число таких дефектов для каждой энергии ПВА. Подсчет дефектов в кристаллите осуществлялся следующим образом. Каждому узлу i идеальной кристаллической решетки ставится в соответствие ячейка Вигнера-Зейца Ci, которая определяется как множество всех точек пространства, расстояние от которых до узла i (с учетом периодических граничных условий) меньше или равно расстоянию до любого другого узла решетки. Отсутствие атомов в ячейке Ci трактуется как вакансия в узле i, попадание более одного атома в ячейку Ci трактуется как наличие собственного межузельного атома (СМА) вблизи узла i. Число точечных дефектов определяется как общее количество ячеек Вигнера-Зейца, не содержащих ни одного атома материала.

Доля “выживших” дефектов, также известная как “каскадная эффективность”, определялась по формуле:

p ^{( E} ПВА )

N ( E ПВА ) f ( E ПВА )

где Е_ПВА – энергия первично-выбитого атома, N(Е_ПВА) – рассчитанное среднее число дефект о в, “выживающих” в каскаде, f(E_nBA) = 0,8 • Е_ПВ А /2E_d – количество атомных смещений по NRT-стандарту [9] (без учета неупругих потерь энергии, которые в рассматриваемом интерва л е энергий ПВА являются незначительными), E d — средняя пороговая энергия смещения. Для средней пороговой энергии смещения мы здесь использовали значение =40 эВ, рекомендуемое стандартом ASTM [10]. Отметим, что используемые нами потенциалы обеспечивают хорошее согласие с этим значением пороговой энергии [7].

Полученные усредненные по направлениям импульса ПВА значения N(ЕПВА) и p(ЕПВА) представлены на рис. 1 и 2, соответственно. Из полученных результатов видно, что везде на рассматриваемом интервале энергий наблюдается рост числа дефектов с увеличением ЕПВА, в то время как каскадная эффективность в основном убывает с ростом ЕПВА. Исключения составляют два “выброса” для сплава Fe-Ni при энергиях 0.5 и 20 кэВ. При этом полученные оценки N(ЕПВА) и p(ЕПВА) для 0.5 кэВ, по всей видимости, занижены, а для 20 кэВ – немного завышены. Оба “выброса”, по всей видимости, носят статистический характер. Отличия в соответствующих оценках для чистого железа и сплава с никелем практически всюду лежат в пределах погрешностей расчета. Из этого можно сделать вывод о том, что присутствие никеля в рассматриваемой концентрации (1.8ат.%) не оказывает влияния на число выживающих дефектов, а, следовательно, и на каскадную эффективность.

Бэкон и др. [11] и Вудинг и др. [12] показали, что для металлов зависимость числа выживших дефектов от энергии ПВА хорошо аппроксимируется степенной функцией

N(E) = A • EB.              (2)

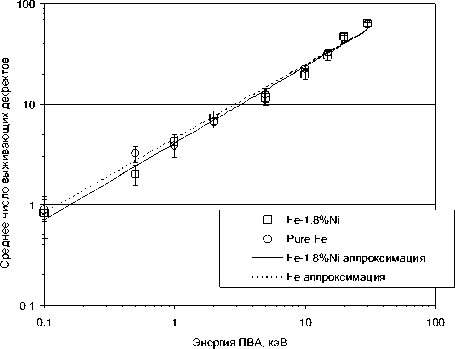
Рис.1. Рассчитанное среднее число “выживающих” дефектов

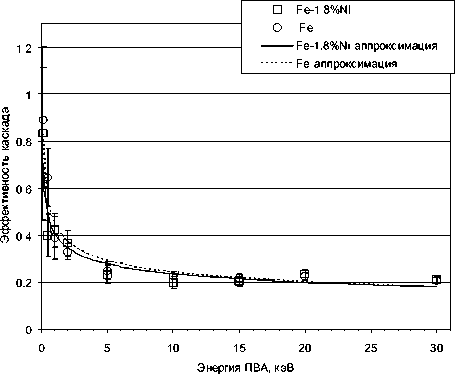
Рис. 2. Каскадная эффективность

Полученные нами результаты также хорошо описываются зависимостями такого вида (см. рис. 1), а именно

N(E) = 4.48• E073 для a-Fe,        (3)

N(E) = 4.08 • E⁰⁷⁶ для сплава Fe-1.8ат.%Ni, (4) где Е – энергия ПВА в кэВ.

Учитывая (1) из формул (3-4) получаем соответствующие аппроксимации для каскадной эффективности p(ЕПВА):

p(E) = 0.448• E' для a-Fe, (5)

p(E) = 0-408 . E ⁰²⁴ для сплава Fe-1.8ат.%Ni. (6)

Известно, что существенный вклад в микроструктурную эволюцию материала под облучением вносит объединение производимых в нем точечных дефектов в кластеры. При моделировании каскадов смещений мы, наряду с оценкой числа “выживающих” дефектов, получили оценки размеров и количества кластеров вакансий и СМА Fe и Ni, остающихся в кристаллите после затухания каскада. Дефекты одного типа считали принадлежащими одному кластеру, если соответствующие им узлы решетки находятся на расстоянии не далее вторых ближайших соседей для вакансий и третьих ближайших соседей для СМА.

На рис. 3 представлены расчетные оценки доли точечных дефектов, образовавших кластеры на момент завершения моделирования каскада. Хорошо видно, что для обеих рассматриваемых систем количество вакансий, участвующих в процессе кластеризации, при энергиях ПВА до 0.5 кэВ превышает число СМА, входящих в кластеры. При более высоких энергиях число вакансий в кластерах становится меньше числа обра- а) СМА

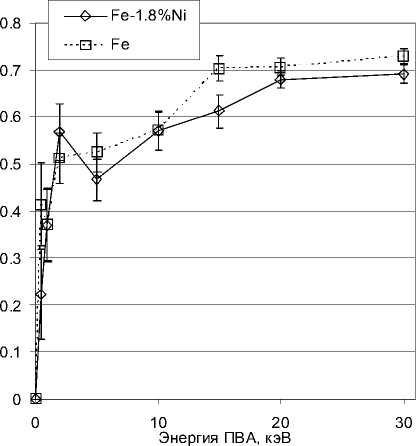
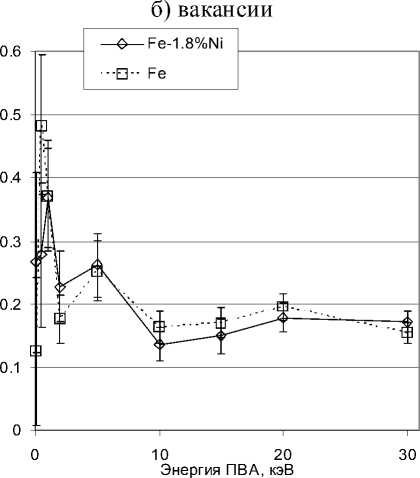
Рис. 3. Доля дефектов, образующих кластеры

зующих кластеры СМА. Отметим, что для всех рассмотренных энергий ПВА доли дефектов обоих типов, попадающих в кластеры, для сплава с никелем и для чистого железа совпадают в пределах погрешности. Исключение составляют только вакансии для энергии ПВА 10 кэВ

ЗАКЛЮЧЕНИЕ

Кратко сформулируем основные результаты работы.

Методом молекулярной динамики проведено моделирование каскадов атомных смещений для сплава Fe-1.8am.%Ni и однокомпонентного а-Fe. Моделирование проведено для начальной температуры системы 600K. Получены оценки числа выживающих дефектов для энергий ПВА до 30 кэВ и результаты по размерам и количеству кластеров вакансий и СМА, образующихся в каскаде смещений.

Полученные зависимости среднего числа выживающих дефектов и каскадной эффективности от энергии ПВА хорошо аппроксимируются степенной функцией. Не выявлено заметного влияния никеля в рассматриваемой концентрации на число точечных дефектов, выживающих в каскаде.

Исследована зависимость каскадной эффективности от энергии ПВА (в диапазоне от 0.1 до 30 КэВ). Наименьшие значения каскадной эффективности наблюдаются для энергий ПВА 10–30 кэВ и составляют = 0.22 и 0.20 - 0.24 для а-Fe и сплава Fe-1.8ат.%Ni соответственно.

Согласно полученным оценкам количество вакансий в кластерах лежит выше числа попадающих в кластеры СМА только для энергий ПВА 0.1-0.5 кэВ, и ниже – для более высоких энергий, причем для энергий выше 10 кэВ это отличие достигает 3.5 раз. Не выявлено значимых отличий в долях кластеризованных дефектов для чистого железа и сплава с никелем.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг, ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы.