Моделирование каскадов атомных смещений в бинарном сплаве Fe-9ат. %Cr методом молекулярной динамики

Феррито-мартенситные стали с быстроспа-дающей наведенной активностью (RAFM) 7-10%-Cr-WVTa являются основными кандидатами для первой стенки и конструкций бланкета будущего реактора синтеза. Хотя RAFM-стали проявляют ряд преимуществ под облучением по сравнению с коммерческими сплавами, низкотемпературное упрочнение при нейтронном облучении сопровождаемое охрупчиванием, снижение ударной вязкости и пластичности остаются основным препятствием для их применения.

Данная работа посвящена моделированию каскадов атомных смещений в бинарном сплаве Fe-9ат.%Cr методом молекулярной динамики. Целью работы является определения ряда параметров первичной радиационной повреждаемости в указанном сплаве с учетом процессов рекомбинации и кластеризации точечных дефектов в каскадах смещений. Моделирование проведено для температуры 300 К.

Молекулярная динамика является одним из наиболее подходящих способов моделирования каскадов атомных смещений. К настоящему времени различными группами исследователе по всему миру проведено большое количество таких исследований применительно к различным ма териалам. Особенно много данных получено для Тихончев Михаил Юрьевич, кандидат физико-математических наук, начальник лаборатории моделирования поведения неорганических материалов.

чистого б-Fe с использованием различных потенциалов межатомного взаимодействия. Моделирование каскадов в сплавах также широко выполняется, хотя для многокомпонентных систем сохраняется проблема подготовки надежных потенциалов. В последние годы опубликовано достаточно большое количество работ, посвященных такому моделированию для системы Fe-Cr (см., например работы [1, 2, 3, 4, 5]). Малерба и др. [1] провели молекулярно динамическое моделирование каскадов смещений в сплаве Fe-10ат.%Cr для энергий первично-выбитого атома (ПВА) до 15 кэВ. Немного позднее Терентьев и др. [2] выполнили расчеты для энергий ПВА до 50 кэВ. Валлениус и др. [3] промоделировали каскады для системы Fe-5ат.%Cr и Fe-20ат.%Cr. В работах [1, 2, 3] использовались потенциалы межатомного взаимодействия на основе метода погруженного атома. Однако потенциал для Fe в работах [1, 2] показывает для собственных межузельных атомов (СМА) большую стабильность гантельной конфигурации <111>, чем <110>, что противоречит экспериментальным результатами и расчетам из первых принципов. Потенциалы в работе [3] дают почти вдвое более высокие энергии образования смешанных “гантелей” внедрений Fe-Cr в матрице a -Fe, чем показывают расчеты из первых принципов. Кроме перечисленного следует особо отметить, что потенциалы межатомного взаимодействия, использованные во всех упомянутых работах, предназначены для моделирования случайного сплава FeCr с заданной концентрацией Cr. Они не воспроизводят кривую энтальпии смешения Fe и Cr во всем диапазоне концентраций. Известно [6], что эта кривая меняет знак при концентрациях Cr ~5-

10%. В настоящей работе используется модифицированная версия потенциала А. Каро и др. [7], хорошо воспроизводящая энергию смешения случайного ферро-магнитного сплава FeCr для произвольной концентрации компонент.

2. МЕТОД МОДЕЛИРОВАНИЯ

Моделирование каскадов атомных смещений проводили методом молекулярной динамики. Мы использовали многотельный потенциал межатомного взаимодействия, предложенный А. Каро и др. [7]. В используемом формализме энергия системы из N атомов записывается как

E tot

= Е FT- ⁽ Е P tj ⁽ r y » ⁺ Т Е h TiTj ⁽ x y V TTj ⁽ Г у ) , (1) i = 1 L       у * i                ² у * i                         J

N

где E_tot – полная потенциальная энергия системы, Ti – тип i -го атома: Fe или Cr, r_Ti – собственная электронная плотность атома T_i как функция расстояния до его центра, F_Ti – фунция внедрения, r_ij – расстояние между атомами i и j , V _TiTi (r) – парный потенциал, V_FeCr =( V_FeFe+V_CrCr )/2. h_TiTj(x) =1, если Ti = Tj , иначе h_TiTj(x) – полином Редлиха-Кистера четвертой степени,

x ij

Fe

p   ,p

tot tot

V p i p j J

Fe где pi - вклад в электронную плотность в узле i tot

( p i ) только от атомов железа.

Базовые потенциалы для Fe и Cr взяты авторами [7] из работ [8] и [3] соответственно. Параметры полинома h_TiTj(x) были подобраны так, чтобы близко воспроизвести кривую энтальпии смешения случайного ферро-магнитного сплава Fe-Cr, рассчитанную методом ab initio из работы [6].

Мы произвели небольшую модификацию описанного потенциала. Во-первых, мы использовали более новую версию потенциала для Fe, взятую из работы [9]. Далее, необходимо аккуратно описать репульсивную часть потенциала для взаимодействий Fe-Cr при небольших (<1 Е) межатомных расстояниях. Это необходимо для моделирования каскадов атомных смещений [10,5]. Для этой цели мы заменили слагаемое h_FeCr ( x)V_FeCr ( r) в формуле (1) следующей функцией.

v^r (x, r)=h (xvcx r)+v (r),       (3)

где Vm£(r) = ^

'F.-Vr), r > r0 cr3 + dr2,0 < r < r0,

V(r) =

Z1Z 2 e2 ’ 4ле 0 r

r Ф (-), a

a (r - r2)3 e3 r,

0 < r < r1

r1 < r < r2

V(r) – экранированный кулоновский парный потенциал для r1 . Длина экранирования a определена согласно работе [11], а функция F(x) – в соответствие подходу Циглера, Берсака и Лит-тмарка [12]. Коэффициенты c, d , а и P подбираются из условия непрерывности соответствующих функций и их первых производных, r₁ =1 Е, r₀ и r₂ – подгоночные параметры. Подгонка проведена под энергии связи смешанных FeCr гантелей внедрений с ориентацией <110> и <111>, рассчитанных Ольссоном и др. [13] методом ab initio. Полученные значения r₀ и r₂ составили 2.22815 и 1.9664 Е соответственно.

3. МОДЕЛИРОВАНИЕ КАСКАДОВ СМЕЩЕНИЙ

Для моделирования каскадов атомных смещений и оценки числа “выживших” дефектов задавались ОЦК кристаллиты Fe-9ат.%Cr, содержащие до = 600000 атомов. При этом расположение атомов разных типов в сплаве носило случайный характер, т.е., каждому атому кристаллита с вероятностью p=0.91 приписывался тип Fe и с вероятностью (1–p) – Cr. При расчётах использовались “периодические” граничные условия. Поэтому, чтобы избежать цикличности возмущений вдоль плотноупакованного направления <111>, кристаллиты задавали в форме прямоугольного параллелепипеда, но не куба. Моделирование проводилось при начальной температуре кристаллита T = 600 K для восьми различных энергий ПВА (Е_ПВА): 0.1, 0.5, 1, 2, 5, 10, 15 и 20 кэВ. Начальную температуру обеспечивали путем задания начальных скоростей атомам кристаллита с последующим молекулярно динамическим моделированием NPT-ансамбля с баростатом и термостатом Берендсена для нулевого давления и температуры 300 К, соответственно, в течении 1 пс с шагом по времени 1 фс. Затем, фиксированному атому (ПВА) релаксированного кристаллита (это мог быть как атом Fe так и Ni) придавали импульс в высокоиндексном направлении <135>.

В ходе моделирования каскадов никакие алгоритмы сброса кинетической энергии для имитации “остывания” кристаллита не использовались. Рост температуры кристаллита составил от = 16 К для Е_П ВА =0.1 кэВ до = 125 К для Е ПВА =20 кэВ. Расчеты проводились с неравномерным шагом по времени, который выбирался так, чтобы он не превосходил 10^-3 пс., и чтобы за один шаг по времени атом с максимальной кинетической энергией смещался не более чем на 0.02 Е. Моделируемое время развития каскада подбиралось так, чтобы обеспечить моделирование всего процесса образования и релаксации дефектов в каскаде вплоть до его затухания.

При моделировании каскада смещений периодически проводился анализ кристаллита, подсчитывалось число дефектов, переживших рекомбинацию в каскаде, и определялось среднее число таких дефектов для каждой энергии ПВА. Подсчет дефектов в кристаллите осуществлялся следующим образом. Каждому узлу i идеальной кристаллической решетки ставится в соответствие ячейка Вигнера-Зейца Ci, которая определяется как множество всех точек пространства, расстояние от которых до узла i (с учетом периодических граничных условий) меньше или равно расстоянию до любого другого узла решетки. Обобщения подобных ячеек известны в математике и физике под названиями ячеек Дирихле и полиэдров Вороного. Отсутствие атомов в ячейке Ci трактуется как вакансия в узле i, попадание более одного атома в ячейку Ci трактуется как наличие внедрений вблизи узла i. Число дефектов определяется как общее количество ячеек Вигне-ра-Зейца, не содержащих ни одного атома материала.

Доля “выживших” дефектов определялась по формуле:

N ( E ПВА )

^{P ( E} ПВА ) "  f ( E пва ) , <⁶⁾ где N(Е_ПВА) – рассчитанное среднее число “выживающих” дефектов, f(E_nBA)=0.8 - E_nBA/(2 E d ) -количество атомных смещений по NRT-стандарту (без учета неупругих потерь энергии, которые в рассматриваемом интервале энергий ПВА являются незначительными).

Величину p(Е_ПВА) в современной литературе часто называют коэффициентом каскадной эффективности. Для пороговой энер г ии смещения мы здесь использовали значение E_d =40 эВ. Полученные усредненные по направлениям импульса ПВА значения N(Е_ПВА) и p(Е_ПВА) представлены на рис. 1 и 2, соответственно, как для рассматриваемого сплава Fe-9ат.%Cr, так и для чистого a -Fe. Из полученных результатов видно, что везде на рассматриваемом интервале энергий наблюдается рост числа дефектов с увеличением Е_ПВА. Несмотря на то, что при Е_ПВА. выше 15 кэВ наблюдается незначительное возрастание доли дефектов, переживших рекомбинацию в каскаде, с учетом погрешностей эту величину можно считать убывающей по Е_ПВА.

Бэкон и др. [14] и Вудинг и др. [15] показали, что для металлов зависимость N(ЕПВА) хорошо аппроксимируется степенной функцией вида

N(E) = A • EB . (7)

Полученные нами результаты также хорошо описываются зависимостями такого вида (см. рис. 1), а именно

N(E) = 5.45 • E⁰⁷¹ , для Fe-9ат.%Cr, (8)

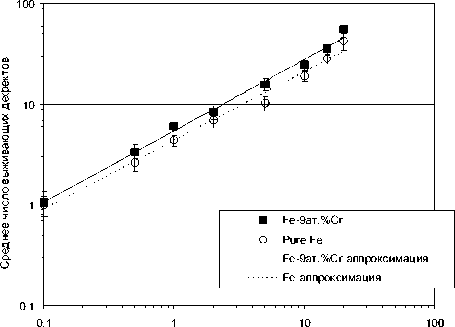
Энергия ПВА, кэВ

Рис. 1. Рассчитанное число “выживающих” дефектов

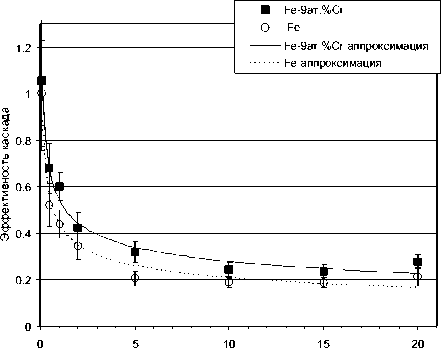
Энергия ПВА, кэВ

Рис. 2. Доля дефектов, переживших рекомбинацию в каскаде смещений

N(E) = 4.36 • E⁰⁶⁸ , для Fe, (9) где Е – энергия ПВА в кэВ.

Учитывая (6) из формул (8-9) получаем соответствующие аппроксимации для зависимости p (Е_ПВА):

N(E) = 5.45 • E 0.29, для Fe-9ат.%Cr, (10) p(E) = 4.36 • E0 32, для Fe, (11) На рис. 3 представлены доли хрома в СМА на момент завершения моделирования эволюции каскада. К этому моменту в кристаллите наблюдается лишь очень незначительная часть “гантелей” внедрений типа Cr-Cr, значительная часть межузельного хрома находится в смешанных “гантелях” Fe-Cr. Следует отметить, что средняя доля Cr в СМА слабо зависит от энергии ПВА и составляет = 22%. Таким образом, концентрация хрома в СМА более чем вдвое превышает его концентрацию в исходной матрице.

Известно, что существенный вклад в микроструктурную эволюцию материала под облучением вносит объединение производимых в нем точечных дефектов в кластеры. При моделировании каскадов смещений мы, наряду с оценкой числа “выживающих” дефектов, получили оцен-

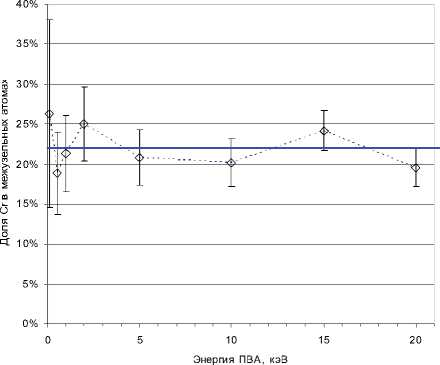
Рис. 3. Доля хрома в СМА на момент затухания каскада

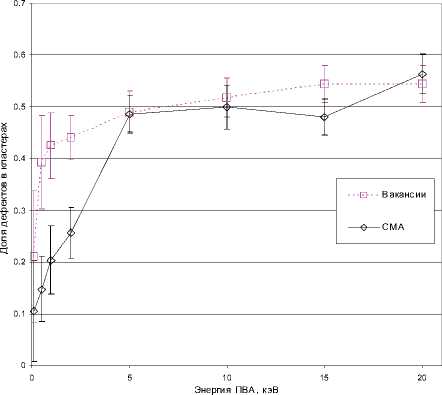
Рис. 4. Доля дефектов, образующих кластеры

ки размеров и количества кластеров внедрений и вакансий, остающихся в кристаллите после затухания каскада. Дефекты одного типа считали принадлежащими одному кластеру, если соответствующие им узлы решетки находятся на расстоянии не далее вторых ближайших соседей для вакансий и третьих ближайших соседей для СМА.

На рис. 4 представлены рассчитанные для сплава Fe-9ат.%Cr доли точечных дефектов, образовавших кластеры на момент завершения моделирования каскадов. Хорошо видно, что при энергиях ПВА 5 кэВ и выше количество вакансий, участвующих в процессе кластеризации, совпадает в пределах погрешности с числом СМА, входящих в кластеры.

• 4.    ЗАКЛЮЧЕНИЕ

В работе методом молекулярной динамики проведено моделирование каскадов атомных смещений в бинарном сплаве Fe-9ат. %Cr для энергий ПВА от 100 эВ до 20 кэВ. При моделировании использовали многотельные межатомные потенциалы межатомного взаимодействия, взятые из работы [7]. Мы модифицировали эти потенциалы для корректного описания взаимодействий на небольших межатомных расстояниях, что важно для моделирования процессов радиационной повреждаемости.

Исследована зависимость доли дефектов, “выживающих” в каскаде смещений, от энергии ПВА (в диапазоне от 0.1 до 20 кэВ). Согласно полученным результатам зависимость числа “выживающих” дефектов хорошо аппроксимируется степенной функцией, что качественно согласуется результатами других исследователей. Значение каскадной эффективности при E_ПВА начиная с 10 кэВ составляет = 0.2. Эта оценка хорошо согласуется с результатами работы [5].

В тоже время она лежит ниже соответствующей оценки = 0.3, полученной в работе [2], и превосходит оценку ~ 0.135 из работы [3]. В обоих случаях отличие может быть объяснено использованием различных потенциалов межатомного взаимодействия. В частности потенциал для Fe в работе [2] показывает для межузельных атомов большую стабильность гантельной конфигурации <111>, чем <110>, что противоречит экспериментальным результатами и ab initio расчетам для a -Fe. Кросс-потенциалы Fe-Cr в работе [3] дает заметно более высокие энергии образования смешанных “гантелей” внедрений Fe-Cr в матрице a -Fe.. Следует также отметить, что оценки как числа “выживающих” в каскаде пар Френкеля, так и каскадная эффективность для системы Fe-9ат.%Cr оказываются несколько выше, чем для чистого a -Fe.

Согласно полученным результатам доля хрома в СМА после прохождения каскада составляет = 22 %, т.е. более чем вдвое превышает долю хрома в исходном сплаве. Эти результаты качественно согласуются с результатами работы [2], но противоположны результатам, полученным в работах [4, 5]. Однако, несмотря на качественное согласие оценки доля Cr в СМА из работы [2] составляют 60 – 70 % для E_ПВА от 1 до 30 кэВ и около 50 % для E_ПВА=50 кэВ. Эти отличия, по всей видимости, являются эффектом разных потенциалов. Для подтверждения или опровержения этих результатов необходимы дальнейшие, в том числе и экспериментальные, исследования.

Получены результаты по размерам и количеству кластеров вакансий и внедрений, образующихся в каскаде смещений, для различных энергий ПВА. Согласно этим результатам, для энергий 5 кэВ и выше не наблюдается значимых отличий между количеством вакансий, участвующих в процессе кластеризации, и числом образующих кластеры СМА.

Полученные результаты могут быть использованы для развития моделей радиационного повреждения сплавов Fe-Cr, в том числе, на основе многомасштабного подхода.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг, ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009 – 2013 годы и при частичной поддержке гранта РФФИ – проект 12-08-97076.